Восьмеричный путь (физика)

В физике восьмеричный путь — это организационная схема для класса субатомных частиц, известных как адроны , которая привела к разработке кварковой модели . И американский физик Мюррей Гелл-Манн , и израильский физик Ювал Нееман независимо и одновременно предложили эту идею в 1961 году. [ ^1]^[2]^[a] Название происходит от статьи Гелл-Манна (1961) и является намеком на Благородный Восьмеричный Путь Буддизма . ^[3]

Фон

К 1947 году физики считали, что у них есть хорошее понимание того, что такое мельчайшие частицы материи. Были электроны , протоны , нейтроны и фотоны (компоненты, которые составляют огромную часть повседневного опыта, такие как атомы и свет), а также несколько нестабильных (то есть, они подвергаются радиоактивному распаду ) экзотических частиц, необходимых для объяснения наблюдений космических лучей, таких как пионы , мюоны и гипотетические нейтрино . Кроме того, открытие позитрона предполагало , что для каждой из них могут существовать античастицы . Было известно, что должно существовать « сильное взаимодействие », чтобы преодолеть электростатическое отталкивание в атомных ядрах. Не все частицы подвержены этому сильному взаимодействию, но те, которые подвержены, называются «адроны», которые теперь далее классифицируются как мезоны (средней массы) и барионы (тяжелого веса).

Но открытие нейтрального каона в конце 1947 года и последующее открытие положительно заряженного каона в 1949 году расширили семейство мезонов неожиданным образом, а в 1950 году лямбда-частица сделала то же самое для семейства барионов. Эти частицы распадаются гораздо медленнее, чем производятся, что является намеком на то, что здесь задействованы два разных физических процесса. Это впервые предположил Абрахам Пайс в 1952 году. В 1953 году Мюррей Гелл-Манн и его коллега из Японии Тадао Накано с Казухико Нисидзимой независимо друг от друга предложили новую сохраняющуюся величину, теперь известную как « странность », во время их попыток понять растущую коллекцию известных частиц. ^[4]^[5]^[b] Тенденция открытия новых мезонов и барионов продолжалась в течение 1950-х годов, поскольку число известных «элементарных» частиц стремительно росло. Физики были заинтересованы в понимании адрон-адронных взаимодействий через сильное взаимодействие. Концепция изоспина , введенная в 1932 году Вернером Гейзенбергом вскоре после открытия нейтрона, использовалась для группировки некоторых адронов в «мультиплеты», но ни одна успешная научная теория пока не охватывала адроны как единое целое. Это было начало хаотического периода в физике элементарных частиц, который стал известен как эпоха « зоопарка частиц ». Восьмеричный путь представлял собой шаг из этой путаницы к кварковой модели , которая оказалась решением.

Организация

Теория группового представления является математической основой восьмеричного пути, но эта довольно техническая математика не нужна для понимания того, как она помогает организовывать частицы. Частицы сортируются по группам как мезоны или барионы. Внутри каждой группы они далее разделяются по их спиновому угловому моменту. Симметричные узоры появляются, когда эти группы частиц имеют график их странности против их электрического заряда . (Это наиболее распространенный способ создания этих графиков сегодня, но изначально физики использовали эквивалентную пару свойств, называемых гиперзарядом и изотопическим спином , последний из которых теперь известен как изоспин .) Симметрия в этих узорах является намеком на базовую симметрию сильного взаимодействия между самими частицами. На графиках ниже точки, представляющие частицы, которые лежат вдоль одной и той же горизонтальной линии, имеют одинаковую странность, $s$ , в то время как точки на тех же диагоналях с левым наклоном имеют один и тот же электрический заряд, $q$ (заданный как кратный элементарного заряда ).

Мезоны

В изначальном восьмеричном способе мезоны были организованы в октеты и синглеты. Это одно из тонких отличий между восьмеричным способом и кварковой моделью, которую он вдохновил, которая предполагает, что мезоны должны быть сгруппированы в нонеты (группы по девять).

Мезонный октет

Восьмеричный способ организует восемь мезонов с наименьшим спином -0 в октет. ^[1]^[6] Это:

К⁰
,
К⁺
,
К⁻
и
К⁰
каоны
π⁺
,
π⁰
, и
π⁻
пионы
η
, эта-мезон

Диаметрально противоположные частицы на диаграмме являются античастицами друг друга, а частицы в центре являются своими собственными античастицами.

Мезон синглетный

Незаряженный, нестранный эта-первичный мезон изначально был классифицирован сам по себе как синглет:

η′

В рамках разработанной позднее кварковой модели его лучше рассматривать как часть мезонного нонета, как упоминалось ранее.

Барионы

Барионный октет

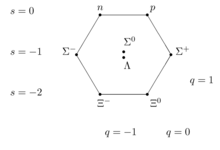
Восьмеричный путь организует спин - ⁠1/ 2 ⁠ барионы в октет. Они состоят из

Декуплет барионов

Организационные принципы восьмеричного пути применимы и к прядильному процессу .3/ 2 ⁠ барионы, образующие декуплет .

Δ⁻
,
Δ⁰
,
Δ⁺
, и
Δ⁺⁺
дельта-барионы
Σ^∗−
,
Σ^∗0
, и
Σ^∗+
сигма-барионы
Ξ^∗−
и
Ξ^∗0
кси барионы
Ω⁻
омега-барион

Однако одна из частиц этого декуплета никогда ранее не наблюдалась, когда был предложен восьмеричный путь. Гелл-Манн назвал эту частицуΩ−и предсказал в 1962 году, что он будет иметь странность −3, электрический заряд −1 и массу около1680 МэВ/ c2 . В 1964 году группа ускорителей частиц в Брукхейвене открыла частицу, близко соответствующую этим предсказаниям ^[^7] . Гелл-Манн получил Нобелевскую премию по физике 1969 года за свою работу по теории элементарных частиц .

Историческое развитие

Разработка

Исторически кварки были мотивированы пониманием симметрии ароматов. Во-первых, было замечено (1961), что группы частиц связаны друг с другом способом, который соответствует теории представлений SU(3) . Из этого был сделан вывод, что существует приблизительная симметрия вселенной, которая параметризуется группой SU(3). Наконец (1964), это привело к открытию трех легких кварков (вверх, вниз и странный), взаимозаменяемых этими преобразованиями SU(3).

Современная интерпретация

Восьмеричный путь можно понимать в современных терминах как следствие симметрии ароматов между различными видами кварков . Поскольку сильная ядерная сила влияет на кварки одинаково независимо от их аромата, замена одного аромата кварка на другой в адроне не должна сильно изменить его массу, при условии, что соответствующие массы кварков меньше масштаба сильного взаимодействия, который справедлив для трех легких кварков. Математически эта замена может быть описана элементами группы SU(3) . Октеты и другие конфигурации адронов являются представлениями этой группы.

Симметрия вкуса

СУ(3)

Существует абстрактное трехмерное векторное пространство:

{\text{верхний кварк}}\rightarrow {\begin{pmatrix}1\\0\\0\end{pmatrix}},\qquad {\text{нижний кварк}}\rightarrow {\begin{pmatrix}0\\1\\0\end{pmatrix}},\qquad {\text{странный кварк}}\rightarrow {\begin{pmatrix}0\\0\\1\end{pmatrix}}

и законы физики приблизительно инвариантны относительно применения к этому пространству унитарного преобразования с детерминантом 1 (иногда называемого вращением аромата ):

{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto A{\begin{pmatrix}x\\y\\z\end{pmatrix}},\quad {\text{where }}A{\text{ is in }}SU(3)

Здесь SU(3) относится к группе Ли 3×3 унитарных матриц с определителем 1 ( специальная унитарная группа ). Например, вращение аромата

A={\begin{pmatrix}~\;~0&1&0\\-1&0&0\\~\;~0&0&1\end{pmatrix}}

это преобразование, которое одновременно превращает все верхние кварки во вселенной в нижние кварки и наоборот. Более конкретно, эти вращения ароматов являются точными симметриями, если рассматривать только сильные взаимодействия, но они не являются по-настоящему точными симметриями вселенной, поскольку три кварка имеют разные массы и разные электрослабые взаимодействия.

Эта приблизительная симметрия называется ароматической симметрией или, более конкретно, ароматической SU(3)-симметрией .

Связь с теорией репрезентации

Предположим, что у нас есть некая частица, например, протон, в квантовом состоянии . Если мы применим одно из вращений аромата A к нашей частице, она перейдет в новое квантовое состояние, которое мы можем назвать . В зависимости от A это новое состояние может быть протоном, нейтроном или суперпозицией протона и нейтрона или различными другими возможностями. Набор всех возможных квантовых состояний охватывает векторное пространство. $|\psi \rangle$ $A|\psi \rangle$

Теория представлений — это математическая теория, описывающая ситуацию, когда элементы группы (здесь — вращения ароматов A в группе SU(3)) являются автоморфизмами векторного пространства (здесь — множества всех возможных квантовых состояний, которые вы получаете при вращении ароматов протона). Поэтому, изучая теорию представлений SU(3), мы можем узнать возможности того, что такое векторное пространство и как на него влияет симметрия ароматов.

Поскольку вращения аромата A являются приблизительными, а не точными симметриями, каждое ортогональное состояние в векторном пространстве соответствует разным видам частиц. В приведенном выше примере, когда протон преобразуется каждым возможным вращением аромата A , оказывается, что он движется вокруг 8-мерного векторного пространства. Эти 8 измерений соответствуют 8 частицам в так называемом «барионном октете» (протон, нейтрон,
Σ⁺
,
Σ⁰
,
Σ⁻
,
Ξ⁻
,
Ξ⁰
,Λ). Это соответствует 8-мерному («октетному») представлению группы SU(3). Поскольку A является приблизительной симметрией, все частицы в этом октете имеют одинаковую массу. ^[8]

Каждая группа Ли имеет соответствующую алгебру Ли , и каждое групповое представление группы Ли может быть отображено в соответствующее представление алгебры Ли в том же векторном пространстве. Алгебра Ли (3) может быть записана как набор 3×3 бесследовых эрмитовых матриц . Физики обычно обсуждают теорию представления алгебры Ли (3) вместо группы Ли SU(3), поскольку первая проще, и они в конечном итоге эквивалентны. ${\mathfrak {su}}$ ${\mathfrak {su}}$

Примечания

^ В статье Гелл-Манна 1961 года, ссылка 6, говорится:
После распространения предварительной версии этой работы (январь 1961 г.) автор узнал о схожей теории, выдвинутой независимо и одновременно Y. Ne'eman ( Nuclear Physics , готовится к публикации). Более раннее использование 3-мерной унитарной группы в связи с моделью Сакаты было сообщено Y. Ohnuki на Рочестерской конференции по физике высоких энергий 1960 г. A. Salam и J. Ward ( Nuovo Cimento , готовится к публикации) рассмотрели связанные с этим вопросы. Автор хотел бы поблагодарить доктора Ne'eman и профессора Salam за сообщение ему своих результатов.
в то время как в самом конце статьи Неемана (1961) говорится:
Я обязан профессору А. Саламу за обсуждения этой проблемы. Фактически, когда я представил ему эту статью, он показал мне исследование, которое он провел по унитарной теории модели Сакаты, рассматриваемой как калибровочная, и, таким образом, производящей аналогичный набор векторных бозонов. Вскоре после того, как была написана настоящая статья, к нам в препринте профессора М. Гелл Манна поступила еще одна версия, использующая 8-представление для барионов, как в этой статье .
^ В сноске в статье Накано и Нисидзимы говорится:
После завершения этой работы из частного письма профессора Намбу профессору Хаякаве авторы узнали, что доктор Гелл-Манн также разработал похожую теорию.

Ссылки

^ ab Gell-Mann, M. (15 марта 1961 г.). «Восьмеричный путь: теория симметрии сильного взаимодействия». Синхротронная лаборатория. Пасадена, Калифорния : Калифорнийский технологический институт . doi :10.2172/4008239. TID-12608; CTSL-20. {{cite journal}}: Цитировать журнал требует |journal=( помощь )
^ Ne'eman, Y. (август 1961). «Вывод сильных взаимодействий из калибровочной инвариантности». Nuclear Physics . 26 (2). Амстердам: North-Holland Publishing Co.: 222–229. Bibcode : 1961NucPh..26..222N. doi : 10.1016/0029-5582(61)90134-1.
^ Янг, Хью Д.; Фридман, Роджер А. (2004). Университетская физика Сирса и Земанского с современной физикой . вклад А. Льюиса Форда (11-е международное издание). Сан-Франциско, Калифорния: Pearson/Addison Wesley. стр. 1689. ISBN 0-8053-8684-XНазвание представляет собой слегка непочтительную отсылку к Благородному Восьмеричному Пути , набору принципов правильной жизни в буддизме .
^ Гелл-Манн, М. (ноябрь 1953 г.). «Изотопический спин и новые нестабильные частицы» (PDF) . Phys. Rev. 92 ( 3): 833–834. Bibcode :1953PhRv...92..833G. doi :10.1103/PhysRev.92.833.
^ Накано, Тадао; Нисидзима, Казухико (ноябрь 1953 г.). «Независимость заряда для V-частиц». Progress of Theoretical Physics . 10 (5): 581–582. Bibcode :1953PThPh..10..581N. doi : 10.1143/PTP.10.581 .
^ Гелл-Манн, М. (1962). «Симметрии барионов и мезонов». Physical Review . 125 (3): 1067. Bibcode :1962PhRv..125.1067G. doi : 10.1103/physrev.125.1067 .
^ Barnes, VE; Connolly, PL; Crennell, DJ; Culwick, BB; Delaney, WC; Fowler, WB; et al. (1964). "Наблюдение гиперона со странностью минус три" (PDF) . Physical Review Letters . 12 (8): 204. Bibcode : 1964PhRvL..12..204B. doi : 10.1103/PhysRevLett.12.204. OSTI 12491965.
^ Гриффитс, Д. (2008). Введение в элементарные частицы (2-е изд.). Wiley-VCH . ISBN 978-3527406012.

Дальнейшее чтение

М. Гелл-Манн; И. Нееман, ред. (1964). Восьмеричный путь. WA Benjamin . LCCN 65013009.(содержит большинство исторических работ по восьмеричному пути и связанным с ним темам, включая формулу массы Гелл-Манна–Окубо .)