Теория Дебая-Хюккеля

Модель, описывающая отклонения от идеальности в растворах электролитов и плазмах

Теория Дебая-Хюккеля была предложена Петером Дебаем и Эрихом Хюккелем в качестве теоретического объяснения отклонений от идеальности в растворах электролитов и плазмах . ^[1] Это линеаризованная модель Пуассона-Больцмана , которая предполагает чрезвычайно упрощенную модель раствора электролита, но тем не менее дает точные предсказания средних коэффициентов активности для ионов в разбавленном растворе. Уравнение Дебая-Хюккеля обеспечивает отправную точку для современных методов лечения неидеальности растворов электролитов. ^[2]

Обзор

В химии растворов электролитов идеальным раствором является раствор, коллигативные свойства которого пропорциональны концентрации растворенного вещества . Реальные растворы могут демонстрировать отклонения от этого типа идеальности. Для того чтобы учесть эти эффекты в термодинамике растворов, была введена концепция активности : тогда свойства пропорциональны активности ионов. Активность, a , пропорциональна концентрации, c . Константа пропорциональности известна как коэффициент активности , . ^[3] ${\displaystyle \gamma }$

${\displaystyle a=\gamma c/c^{0}}$

В идеальном растворе электролита коэффициенты активности всех ионов равны единице. Идеальность раствора электролита может быть достигнута только в очень разбавленных растворах. Неидеальность более концентрированных растворов возникает в основном (но не исключительно) из-за того, что ионы противоположного заряда притягиваются друг к другу из-за электростатических сил, в то время как ионы одинакового заряда отталкиваются. В результате ионы не распределены хаотично по всему раствору, как это было бы в идеальном растворе.

Коэффициенты активности отдельных ионов не могут быть измерены экспериментально, поскольку раствор электролита должен содержать как положительно заряженные ионы, так и отрицательно заряженные ионы. Вместо этого определяется средний коэффициент активности. Например, с электролитом NaCl ${\displaystyle \gamma _{\pm }}$

${\displaystyle \gamma _{\pm }=\left(\gamma _{\mathrm {Na^{+}} }\gamma _{\mathrm {Cl^{-}} }\right)^{1/2}}$

В общем случае средний коэффициент активности полностью диссоциированного электролита формулы A _n B _m определяется по формуле ^[4]

${\displaystyle \gamma _{\pm }=\left({\gamma _{A}}^{n}{\gamma _{B}}^{m}\right)^{1/(n+m)}}$

Коэффициенты активности сами по себе являются функциями концентрации, поскольку количество межионного взаимодействия увеличивается с ростом концентрации электролита. Дебай и Хюккель разработали теорию, с помощью которой можно было рассчитать коэффициенты активности отдельных ионов. Рассчитав из них средние коэффициенты активности, теорию можно было проверить с помощью экспериментальных данных. Было обнаружено, что она дает превосходное согласие для «разбавленных» растворов.

Модель

Идеализированное представление раствора электролита 1:1

Описание теории Дебая-Хюккеля включает в себя очень подробное обсуждение предположений и их ограничений, а также математическое развитие и приложения. ^[5]

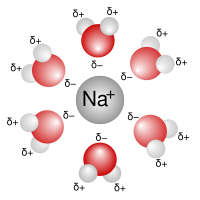
На рисунке показан снимок двухмерного сечения идеализированного раствора электролита. Ионы показаны в виде сфер с единичным электрическим зарядом. Растворитель (бледно-голубой) показан как однородная среда без структуры. В среднем каждый ион окружен ионами с противоположным зарядом более тесно, чем ионами с одинаковым зарядом. Эти концепции были развиты в количественную теорию, включающую ионы с зарядом z ₁ e ⁺ и z ₂ e ⁻ , где z может быть любым целым числом. Основное предположение заключается в том, что отклонение от идеальности обусловлено электростатическими взаимодействиями между ионами, опосредованными законом Кулона : сила взаимодействия между двумя электрическими зарядами, разделенными расстоянием r в среде с относительной диэлектрической проницаемостью ε _{r ,} определяется выражением ^[6]

${\displaystyle {\text{force}}={\frac {z_{1}z_{2}e^{2}}{4\pi \epsilon _{0}\epsilon _{r}r^{2}}}}$

Также предполагается, что

• Растворенное вещество полностью диссоциировано; является сильным электролитом .
• Ионы имеют сферическую форму и не поляризуются окружающим электрическим полем . Сольватация ионов игнорируется, за исключением случаев, когда она определяет эффективные размеры ионов.
• Растворитель не играет никакой роли, кроме обеспечения среды с постоянной относительной диэлектрической проницаемостью ( диэлектрической проницаемостью ).
• Электрострикции нет .
• Отдельные ионы, окружающие «центральный» ион, можно представить в виде статистически усредненного облака непрерывной плотности заряда с минимальным расстоянием наибольшего сближения.

Последнее предположение означает, что каждый катион окружен сферически симметричным облаком других ионов. Облако имеет чистый отрицательный заряд. Аналогично каждый анион окружен облаком с чистым положительным зарядом. ^[7]

Математическое развитие

Отклонение от идеальности принимается как функция потенциальной энергии, возникающей в результате электростатических взаимодействий между ионами и окружающими их облаками. Для расчета этой энергии необходимо выполнить два шага.

Первым шагом является задание электростатического потенциала для иона j с помощью уравнения Пуассона

${\displaystyle \nabla ^{2}\psi _{j}(r)=-{\frac {1}{\epsilon _{0}\epsilon _{r}}}\rho _{j}(r)}$

ψ( r ) — это полный потенциал на расстоянии r от центрального иона, а ρ( r ) — это усредненная плотность заряда окружающего облака на этом расстоянии. Для применения этой формулы необходимо, чтобы облако имело сферическую симметрию, то есть плотность заряда была функцией только расстояния от центрального иона, поскольку это позволяет записать уравнение Пуассона в терминах сферических координат без угловой зависимости. ^[8]

Вторым шагом является расчет плотности заряда с помощью распределения Больцмана .

${\displaystyle n'_{i}=n_{i}\exp \left({\frac {-z_{i}e\psi _{j}(r)}{k_{\rm {B}}T}}\right)}$

где k _B — постоянная Больцмана , а T — температура. Это распределение также зависит от потенциала ψ( r ), и это вносит серьезную трудность в терминах принципа суперпозиции . Тем не менее, эти два уравнения можно объединить, чтобы получить уравнение Пуассона–Больцмана . ^[9]

${\displaystyle \nabla ^{2}\psi _{j}(r)=-{\frac {1}{\epsilon _{0}\epsilon _{r}}}\sum _{i}\left\{n_{i}(z_{i}e)\exp \left({\frac {-z_{i}e\psi _{j}(r)}{k_{\rm {B}}T}}\right)\right\}}$

Решение этого уравнения далеко не прямолинейно. Дебай и Хюккель разложили экспоненту как усеченный ряд Тейлора до первого порядка. Член нулевого порядка исчезает, поскольку решение в среднем электрически нейтрально (так что Σ n _i z _i = 0), что оставляет нам только член первого порядка. Результат имеет вид уравнения Гельмгольца ^[10]

${\displaystyle \nabla ^{2}\psi _{j}(r)=\kappa ^{2}\psi _{j}(r)\qquad {\text{with}}\qquad \kappa ^{2}={\frac {e^{2}}{\epsilon _{0}\epsilon _{r}k_{\rm {B}}T}}\sum _{i}n_{i}z_{i}^{2}}$,

которое имеет аналитическое решение . Это уравнение применимо к электролитам с равным числом ионов каждого заряда. Несимметричные электролиты требуют еще одного члена с ψ ² . Для симметричных электролитов это сводится к модифицированному сферическому уравнению Бесселя

${\displaystyle (\partial _{r}^{2}+{\frac {2}{r}}\partial _{r}-\kappa ^{2})\psi _{j}=0\qquad {\text{with solutions}}\qquad \psi _{j}(r)=A'{\frac {e^{-\kappa r}}{r}}+A''{\frac {e^{\kappa r}}{r}}}$

Коэффициенты и фиксируются граничными условиями. Так как , не должны расходиться, то . При , что является расстоянием наибольшего сближения ионов, сила, действующая со стороны заряда, должна быть уравновешена силой других ионов, налагая , откуда находим, получая ${\displaystyle A'}$ ${\displaystyle A''}$ ${\displaystyle r\rightarrow \infty }$ ${\displaystyle \psi }$ ${\displaystyle A''=0}$ ${\displaystyle r=a_{0}}$ ${\displaystyle \partial _{r}\psi _{j}(a_{0})=-z_{j}e/(4\pi \epsilon _{0}\epsilon _{r}a_{0}^{2})}$ ${\displaystyle A'}$

${\displaystyle \psi _{j}(r)={\frac {z_{j}e}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {e^{\kappa a_{0}}}{1+\kappa a_{0}}}{\frac {e^{-\kappa r}}{r}}}$

Электростатическая потенциальная энергия иона равна ${\displaystyle u_{j}}$ ${\displaystyle r=0}$

${\displaystyle u_{j}=z_{j}e{\Big (}\psi _{j}(a_{0})-{\frac {z_{j}e}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {1}{a_{0}}}{\Big )}=-{\frac {z_{j}^{2}e^{2}}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {\kappa }{1+\kappa a_{0}}}}$

Это потенциальная энергия одного иона в растворе. Многозарядное обобщение из электростатики дает выражение для потенциальной энергии всего раствора. Средний коэффициент активности определяется логарифмом этой величины следующим образом ^[11]

Экспериментальные значения для KBr при 25°C (точки) ^[12] и предельный закон Дебая-Хюккеля (цветная линия) ${\displaystyle \log \gamma _{\pm }}$

${\displaystyle \log _{10}\gamma _{\pm }=-Az_{j}^{2}{\frac {\sqrt {I}}{1+Ba_{0}{\sqrt {I}}}}}$

${\displaystyle A={\frac {e^{2}B}{2.303\times 8\pi \epsilon _{0}\epsilon _{r}k_{\rm {B}}T}}}$

${\displaystyle B=\left({\frac {2e^{2}N}{\epsilon _{0}\epsilon _{r}k_{\rm {B}}T}}\right)^{1/2}}$

где I — ионная сила , а a ₀ — параметр, который представляет расстояние наибольшего сближения ионов. Для водных растворов при 25 °C A = 0,51 моль ^−1/ 2 дм3 ^/2 и B = 3,29 нм ⁻¹ моль ^−1/ 2 дм3 ^{/2 [13]}

${\displaystyle A}$— константа, зависящая от температуры. Если выражается через моляльность, а не молярность (как в уравнении выше и в остальной части этой статьи), то экспериментальное значение для воды равно 25 °C. Обычно используют логарифм по основанию 10, в этом случае мы разлагаем на множители , поэтому A равно . Множитель перед в уравнении относится к случаю, когда размеры равны . Когда размеры равны , множитель необходимо опустить из уравнения ^{[14] : раздел 2.5.2} ${\displaystyle I}$ ${\displaystyle A}$ ${\displaystyle 1.172{\text{ mol}}^{-1/2}{\text{kg}}^{1/2}}$ ${\displaystyle \ln 10}$ ${\displaystyle 0.509{\text{ mol}}^{-1/2}{\text{kg}}^{1/2}}$ ${\displaystyle 10^{3}}$ ${\displaystyle I/2}$ ${\displaystyle I}$ ${\displaystyle {\text{mol}}/{\text{dm}}^{3}}$ ${\displaystyle I}$ ${\displaystyle {\text{mole}}/{\text{m}}^{3}}$ ${\displaystyle 10^{3}}$

Наиболее существенным аспектом этого результата является предсказание того, что средний коэффициент активности является функцией ионной силы, а не концентрации электролита. Для очень низких значений ионной силы значение знаменателя в выражении выше становится почти равным единице. В этой ситуации средний коэффициент активности пропорционален квадратному корню ионной силы. Это известно как предельный закон Дебая-Хюккеля. В этом пределе уравнение задается следующим образом ^{[14] : раздел 2.5.2}

$${\displaystyle \ln(\gamma _{i})=-{\frac {z_{i}^{2}q^{2}\kappa }{8\pi \varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=-{\frac {z_{i}^{2}q^{3}N_{\text{A}}^{1/2}}{4\pi (\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T)^{3/2}}}{\sqrt {10^{3}{\frac {I}{2}}}}=-Az_{i}^{2}{\sqrt {I}},}$$

Избыточное осмотическое давление, полученное из теории Дебая-Хюккеля, выражено в единицах СГС : ^[15] Таким образом, общее давление представляет собой сумму избыточного осмотического давления и идеального давления . Осмотический коэффициент тогда определяется как $${\displaystyle P^{\text{ex}}=-{\frac {k_{\text{B}}T\kappa _{\text{cgs}}^{3}}{24\pi }}=-{\frac {k_{\text{B}}T\left({\frac {4\pi \sum _{j}c_{j}q_{j}}{\varepsilon _{0}\varepsilon _{r}k_{\text{B}}T}}\right)^{3/2}}{24\pi }}.}$$ ${\textstyle P^{\text{id}}=k_{\text{B}}T\sum _{i}c_{i}}$ $${\displaystyle \phi ={\frac {P^{\text{id}}+P^{\text{ex}}}{P^{\text{id}}}}=1+{\frac {P^{\text{ex}}}{P^{\text{id}}}}.}$$

Безразмерность

Берем дифференциальное уравнение из предыдущего (как указано выше, уравнение справедливо только для низких концентраций): $${\displaystyle {\frac {\partial ^{2}\varphi (r)}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial \varphi (r)}{\partial r}}={\frac {Iq\varphi (r)}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=\kappa ^{2}\varphi (r).}$$

Использование теоремы Букингема π для этой задачи приводит к следующим безразмерным группам: называется приведенным скалярным электрическим потенциальным полем. называется приведенным радиусом. Существующие группы могут быть рекомбинированы для формирования двух других безразмерных групп для подстановки в дифференциальное уравнение. Первая — это то, что можно было бы назвать квадратом приведенной обратной длины экранирования , . Вторая могла бы быть названа приведенным центральным зарядом иона (с заглавной буквы Z). Обратите внимание, что, хотя уже безразмерно, без подстановки, приведенной ниже, дифференциальное уравнение все равно было бы размерным. $${\displaystyle {\begin{aligned}\pi _{1}&={\frac {q\varphi (r)}{k_{\text{B}}T}}=\Phi (R(r))\\\pi _{2}&=\varepsilon _{r}\\\pi _{3}&={\frac {ak_{\text{B}}T\varepsilon _{0}}{q^{2}}}\\\pi _{4}&=a^{3}I\\\pi _{5}&=z_{0}\\\pi _{6}&={\frac {r}{a}}=R(r).\end{aligned}}}$$ ${\displaystyle \Phi }$ ${\displaystyle R}$ ${\displaystyle (\kappa a)^{2}}$ ${\displaystyle Z_{0}}$ ${\displaystyle z_{0}}$

$${\displaystyle {\frac {\pi _{4}}{\pi _{2}\pi _{3}}}={\frac {a^{2}q^{2}I}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=(\kappa a)^{2}}$$ $${\displaystyle {\frac {\pi _{5}}{\pi _{2}\pi _{3}}}={\frac {z_{0}q^{2}}{4\pi a\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}=Z_{0}}$$

Чтобы получить безразмерное дифференциальное уравнение и начальные условия, используйте группы для исключения в пользу , затем исключения в пользу , выполняя цепное правило и подставляя , затем исключения в пользу (цепное правило не требуется), затем исключения в пользу , затем исключения в пользу . Полученные уравнения следующие: ${\displaystyle \pi }$ ${\displaystyle \varphi (r)}$ ${\displaystyle \Phi (R(r))}$ ${\displaystyle R(r)}$ ${\displaystyle r}$ ${\displaystyle {R^{\prime }}(r)=a}$ ${\displaystyle r}$ ${\displaystyle R}$ ${\displaystyle I}$ ${\displaystyle (\kappa a)^{2}}$ ${\displaystyle z_{0}}$ ${\displaystyle Z_{0}}$ $${\displaystyle {\frac {\partial \Phi (R)}{\partial R}}{\bigg |}_{R=1}=-Z_{0}}$$ $${\displaystyle \Phi (\infty )=0}$$ $${\displaystyle {\frac {\partial ^{2}\Phi (R)}{\partial R^{2}}}+{\frac {2}{R}}{\frac {\partial \Phi (R)}{\partial R}}=(\kappa a)^{2}\Phi (R).}$$

Для поваренной соли в 0,01 М растворе при 25 °C типичное значение составляет 0,0005636, тогда как типичное значение составляет 7,017, что подчеркивает тот факт, что при низких концентрациях является целью для приближения нулевого порядка величины, такого как анализ возмущений. К сожалению, из-за граничного условия на бесконечности регулярное возмущение не работает. То же граничное условие не позволяет нам найти точное решение уравнений. Однако сингулярное возмущение может работать. ^{[ требуется пояснение ] [ требуется цитата ]} ${\displaystyle (\kappa a)^{2}}$ ${\displaystyle Z_{0}}$ ${\displaystyle (\kappa a)^{2}}$

Ограничения и расширения

Первая сольватная оболочка иона натрия , растворенного в воде. Атомы кислорода расположены в вершинах октаэдра с ионом натрия в его центре

Это уравнение для дает удовлетворительное согласие с экспериментальными измерениями для низких концентраций электролитов, обычно менее 10−3 ^моль /л. Отклонения от теории происходят при более высоких концентрациях и с электролитами, которые производят ионы с более высокими зарядами, особенно несимметричными электролитами. По сути, эти отклонения происходят из-за того, что модель слишком упрощена , поэтому мало что можно получить, внося небольшие корректировки в модель. ^[16] Отдельные предположения могут быть оспорены в свою очередь. ${\displaystyle \log \gamma _{\pm }}$

• Полная диссоциация. Ионная ассоциация может иметь место, особенно с ионами с большим зарядом. Это было подробно рассмотрено Нильсом Бьеррумом . Длина Бьеррума — это расстояние, при котором электростатическое взаимодействие между двумя ионами сравнимо по величине с kT .
• Слабые электролиты. Слабым электролитом является тот, который не полностью диссоциирован. Как таковой, он имеет константу диссоциации . Константу диссоциации можно использовать для расчета степени диссоциации и, следовательно, внесения необходимой поправки, необходимой для расчета коэффициентов активности. ^[17]
• Ионы имеют сферическую форму, а не точечные заряды и не поляризованы . Многие ионы, такие как ион нитрата , NO ₃ ⁻ , не являются сферическими. Многоатомные ионы также поляризуемы.
• Роль растворителя. Растворитель не является бесструктурной средой, а состоит из молекул. Молекулы воды в водном растворе являются как диполярными , так и поляризуемыми. Как катионы, так и анионы имеют сильную первичную сольватную оболочку и более слабую вторичную сольватную оболочку. Взаимодействия ионов и растворителя игнорируются в теории Дебая-Хюккеля.

Более того, ионный радиус предполагается пренебрежимо малым, но при более высоких концентрациях ионный радиус становится сравнимым с радиусом ионной атмосферы . Большинство расширений теории Дебая–Хюккеля носят эмпирический характер. Они обычно позволяют следовать уравнению Дебая–Хюккеля при низкой концентрации и добавляют дополнительные члены в некоторой степени ионной силы для соответствия экспериментальным наблюдениям. Основными расширениями являются уравнение Дэвиса , уравнения Питцера и теория специфического взаимодействия ионов .

Одно из таких расширенных уравнений Дебая-Хюккеля задается следующим образом: где его десятичный логарифм — коэффициент активности, — целый заряд иона (1 для H ⁺ , 2 для Mg ²⁺ и т. д.), — ионная сила водного раствора, — размер или эффективный диаметр иона в ангстремах . Эффективный гидратированный радиус иона, a — радиус иона и его тесно связанных молекул воды. Большие ионы и менее высокозаряженные ионы связывают воду менее прочно и имеют меньшие гидратированные радиусы, чем более мелкие, более высокозаряженные ионы. Типичные значения составляют 3Å для таких ионов, как H ⁺ , Cl ⁻ , CN ⁻ , и HCOO ⁻ . Эффективный диаметр для иона гидроксония составляет 9Å. и являются константами со значениями соответственно 0,5085 и 0,3281 при 25 °C в воде ^[1] . $${\displaystyle -\log _{10}(\gamma )={\frac {A|z_{+}z_{-}|{\sqrt {I}}}{1+Ba{\sqrt {I}}}}}$$ ${\displaystyle \gamma }$ ${\displaystyle z}$ ${\displaystyle I}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle B}$

Расширенное уравнение Дебая-Хюккеля дает точные результаты для μ ≤ 0,1. Для растворов с большей ионной силой следует использовать уравнения Питцера . В этих растворах коэффициент активности может фактически увеличиваться с ионной силой.

График Дебая-Хюккеля с различными значениями заряда иона Z и диаметра иона a

Уравнение Дебая–Хюккеля нельзя использовать в растворах поверхностно-активных веществ , где наличие мицелл влияет на электрохимические свойства системы (даже грубая оценка завышает γ примерно на 50%).

Смеси электролитов

Теория может быть применена также к разбавленным растворам смешанных электролитов. Для этой цели использовались измерения понижения точки замерзания . ^[18]

Проводимость

Силы, действующие на заряженный ион или облако, движущееся в электрическом поле

Рассмотрение, данное до сих пор, относится к системе, не подверженной внешнему электрическому полю. При измерении проводимости система подвергается воздействию осциллирующего внешнего поля из-за приложения переменного напряжения к электродам, погруженным в раствор. Дебай и Хюккель модифицировали свою теорию в 1926 году, а их теория была дополнительно модифицирована Ларсом Онзагером в 1927 году. Все постулаты исходной теории были сохранены. Кроме того, предполагалось, что электрическое поле вызывает искажение облака зарядов от сферической симметрии. ^[19] Приняв это во внимание вместе с конкретными требованиями движущихся ионов, такими как вязкость и электрофоретические эффекты, Онзагер смог вывести теоретическое выражение для учета эмпирического соотношения, известного как закон Кольрауша , для молярной проводимости, Λ _m .

${\displaystyle \Lambda _{m}=\Lambda _{m}^{0}-K{\sqrt {c}}}$

${\displaystyle \Lambda _{m}^{0}}$известна как предельная молярная проводимость, K — эмпирическая константа, а c — концентрация электролита. Ограничение здесь означает «на пределе бесконечного разбавления»). Выражение Онзагера:

${\displaystyle \Lambda _{m}=\Lambda _{m}^{0}-(A+B\Lambda _{m}^{0}){\sqrt {c}}}$

где A и B — константы, зависящие только от известных величин, таких как температура, заряды ионов, диэлектрическая проницаемость и вязкость растворителя. Это известно как уравнение Дебая–Хюккеля–Онзагера. Однако это уравнение применимо только к очень разбавленным растворам и было в значительной степени заменено другими уравнениями, созданными Фуоссом и Онзагером в 1932 и 1957 годах и позже. ^[20]

Краткое изложение первой статьи Дебая и Хюккеля по теории разбавленных электролитов

Английское название статьи — «On the Theory of Electrolytes. I. Freezing Point Depression and Related Phenomena». Первоначально она была опубликована в 1923 году в 24-м томе немецкоязычного журнала Physikalische Zeitschrift . Английский перевод ^{[21] : 217–63} статьи включен в книгу сборника статей, подаренных Дебаю «его учениками, друзьями и издателями по случаю его семидесятилетия 24 марта 1954 года». ^{[21] : xv} Другой английский перевод был завершен в 2019 году. ^[22] Статья посвящена расчету свойств растворов электролитов, находящихся под воздействием электрических полей, индуцированных ионами, то есть она посвящена электростатике .

В том же году, когда они впервые опубликовали эту статью, Дебай и Хюккель (далее D&H) также опубликовали статью, в которой изложили свою первоначальную характеристику растворов под влиянием электрических полей под названием «К теории электролитов. II. Предельный закон для электропроводности», но эта последующая статья (пока) здесь не рассматривается.

В следующем резюме (пока еще неполном и непроверенном) используются современные обозначения и терминология, как из химии, так и из математики, чтобы избежать путаницы. Кроме того, за несколькими исключениями для улучшения ясности, подразделы в этом резюме являются (очень) сжатыми версиями тех же подразделов оригинальной статьи.

Введение

D&H отмечают, что формула Гульдберга-Вааге для электролитных видов в равновесии химической реакции в классической форме имеет вид ^{[21] : 221} , где $${\displaystyle \prod _{i=1}^{s}x_{i}^{\nu _{i}}=K,}$$

• ${\textstyle \prod }$это обозначение для умножения ,
• ${\displaystyle i}$является фиктивной переменной, указывающей вид,
• ${\displaystyle s}$- число видов, участвующих в реакции,
• ${\displaystyle x_{i}}$мольная доля видов , ${\displaystyle i}$
• ${\displaystyle \nu _{i}}$- стехиометрический коэффициент видов , ${\displaystyle i}$
• K — константа равновесия .

D&H утверждает, что из-за «взаимных электростатических сил между ионами» необходимо модифицировать уравнение Гульдберга–Вааге, заменив его на , где — общий коэффициент активности, а не «специальный» коэффициент активности (отдельный коэффициент активности, связанный с каждым видом) — который используется в современной химии с 2007 года . ${\displaystyle K}$ ${\displaystyle \gamma K}$ ${\displaystyle \gamma }$^[update]

Соотношение между и коэффициентами специальной активности равно ^{[21] : 248} ${\displaystyle \gamma }$ ${\displaystyle \gamma _{i}}$ $${\displaystyle \log(\gamma )=\sum _{i=1}^{s}\nu _{i}\log(\gamma _{i}).}$$

Основы

D&H используют свободные энтропии Гельмгольца и Гиббса и для выражения влияния электростатических сил в электролите на его термодинамическое состояние. В частности, они разделяют большинство термодинамических потенциалов на классические и электростатические термины: где ${\displaystyle \Phi }$ ${\displaystyle \Xi }$ $${\displaystyle \Phi =S-{\frac {U}{T}}=-{\frac {A}{T}},}$$

• ${\displaystyle \Phi }$свободная энтропия Гельмгольца ,
• ${\displaystyle S}$это энтропия ,
• ${\displaystyle U}$это внутренняя энергия ,
• ${\displaystyle T}$это температура ,
• ${\displaystyle A}$свободная энергия Гельмгольца .

D&H дает полный дифференциал как ^{[21] : 222} , где ${\displaystyle \Phi }$ $${\displaystyle d\Phi ={\frac {P}{T}}\,dV+{\frac {U}{T^{2}}}\,dT,}$$

• ${\displaystyle P}$это давление ,
• ${\displaystyle V}$это объем .

По определению полного дифференциала это означает то, что пригодится в дальнейшем. $${\displaystyle {\frac {P}{T}}={\frac {\partial \Phi }{\partial V}},}$$ $${\displaystyle {\frac {U}{T^{2}}}={\frac {\partial \Phi }{\partial T}},}$$

Как было сказано ранее, внутренняя энергия делится на две части: ^{[21] : 222} , где $${\displaystyle U=U_{k}+U_{e}}$$

• ${\displaystyle k}$указывает на классическую часть,
• ${\displaystyle e}$указывает на электрическую часть.

Аналогично свободная энтропия Гельмгольца также делится на две части: $${\displaystyle \Phi =\Phi _{k}+\Phi _{e}.}$$

D&H утверждают, не приводя логику, что ^{[21] : 222} $${\displaystyle \Phi _{e}=\int {\frac {U_{e}}{T^{2}}}\,dT.}$$

Казалось бы, без какого-либо обоснования, $${\displaystyle \Phi _{e}=\int {\frac {P_{e}}{T}}\,dV+\int {\frac {U_{e}}{T^{2}}}\,dT.}$$

Не упоминая об этом конкретно, D&H позже приводят то, что может быть требуемым (вышеуказанным) обоснованием, утверждая , что предположение о том, что растворитель несжимаем. ${\displaystyle \Phi _{e}=\Xi _{e}}$

Определение свободной энтропии Гиббса таково ^{[21] : 222–3,} где — свободная энергия Гиббса . ${\displaystyle \Xi }$ $${\displaystyle \Xi =S-{\frac {U+PV}{T}}=\Phi -{\frac {PV}{T}}=-{\frac {G}{T}},}$$ ${\displaystyle G}$

D&H дает полный дифференциал как ^{[21] : 222} ${\displaystyle \Xi }$ $${\displaystyle d\Xi =-{\frac {V}{T}}\,dP+{\frac {U+PV}{T^{2}}}\,dT.}$$

В этом месте D&H отмечают, что для воды, содержащей 1 моль на литр хлорида калия (номинальное давление и температура не указаны), электрическое давление составляет 20 атмосфер. Кроме того, они отмечают, что этот уровень давления дает относительное изменение объема 0,001. Поэтому они пренебрегают изменением объема воды из-за электрического давления, записывая ^{[21] : 223} и ставя ${\displaystyle P_{e}}$ $${\displaystyle \Xi =\Xi _{k}+\Xi _{e},}$$ $${\displaystyle \Xi _{e}=\Phi _{e}=\int {\frac {U_{e}}{T^{2}}}\,dT.}$$

D&H говорят, что, согласно Планку, классическая часть свободной энтропии Гиббса равна ^{[21] : 223} , где $${\displaystyle \Xi _{k}=\sum _{i=0}^{s}N_{i}(\xi _{i}-k_{\text{B}}ln(x_{i})),}$$

• ${\displaystyle i}$это вид,
• ${\displaystyle s}$количество различных типов частиц в растворе,
• ${\displaystyle N_{i}}$- число частиц вида i ,
• ${\displaystyle \xi _{i}}$- это специфическая для частиц свободная энтропия Гиббса вида i ,
• ${\displaystyle k_{\text{B}}}$постоянная Больцмана ,
• ${\displaystyle x_{i}}$мольная доля вида i .

Вид ноль — растворитель. Определение следующее, где строчные буквы указывают на специфические для частиц версии соответствующих обширных свойств: ^{[21] : 223} ${\displaystyle \xi _{i}}$ $${\displaystyle \xi _{i}=s_{i}-{\frac {u_{i}+Pv_{i}}{T}}.}$$

D&H этого не утверждает, но функциональная форма для может быть выведена из функциональной зависимости химического потенциала компонента идеальной смеси от его молярной доли. ^[23] ${\displaystyle \Xi _{k}}$

D&H отмечают, что внутренняя энергия раствора понижается за счет электрического взаимодействия его ионов, но этот эффект не может быть определен с помощью кристаллографического приближения для расстояний между разнородными атомами (кубический корень из отношения общего объема к числу частиц в объеме). Это происходит потому, что в жидком растворе больше теплового движения, чем в кристалле. Тепловое движение имеет тенденцию размывать естественную решетку, которая в противном случае была бы построена ионами. Вместо этого D&H вводит понятие ионной атмосферы или облака. Подобно кристаллической решетке, каждый ион все еще пытается окружить себя противоположно заряженными ионами, но в более свободной форме; на небольших расстояниях от положительных ионов с большей вероятностью можно найти отрицательные ионы и наоборот. ^{[21] : 225} ${\displaystyle U}$

Потенциальная энергия произвольного ионного раствора

Электронейтральность раствора требует, чтобы ^{[21] : 233} где $${\displaystyle \sum _{i=1}^{s}N_{i}z_{i}=0,}$$

• ${\displaystyle N_{i}}$— общее число ионов вида i в растворе,
• ${\displaystyle z_{i}}$- зарядовое число вида i .

Чтобы переместить ион вида i , изначально находящийся далеко, в точку внутри ионного облака, требуется энергия взаимодействия в размере , где — элементарный заряд , а — значение скалярного электрического потенциального поля в . Если бы электрические силы были единственным фактором, то конфигурация всех ионов с минимальной энергией была бы достигнута в плотноупакованной решетчатой ​​конфигурации. Однако ионы находятся в тепловом равновесии друг с другом и относительно свободны для перемещения. Таким образом, они подчиняются статистике Больцмана и образуют распределение Больцмана . Плотности чисел всех видов изменяются по сравнению с их объемными (общими средними) значениями на соответствующий фактор Больцмана , где — постоянная Больцмана , а — температура. ^[24] Таким образом, в каждой точке облака ^{[21] : 233} ${\displaystyle P}$ ${\displaystyle z_{i}q\varphi }$ ${\displaystyle q}$ ${\displaystyle \varphi }$ ${\displaystyle P}$ ${\displaystyle n_{i}}$ ${\displaystyle n_{i}^{0}}$ ${\displaystyle e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}}$ ${\displaystyle k_{\text{B}}}$ ${\displaystyle T}$ $${\displaystyle n_{i}={\frac {N_{i}}{V}}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}=n_{i}^{0}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}.}$$

Обратите внимание, что в пределе бесконечной температуры все ионы распределены равномерно, без учета их электростатических взаимодействий. ^{[21] : 227}

Плотность заряда связана с числовой плотностью: ^{[21] : 233} $${\displaystyle \rho =\sum _{i}z_{i}qn_{i}=\sum _{i}z_{i}qn_{i}^{0}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}.}$$

При объединении этого результата для плотности заряда с уравнением Пуассона из электростатики получается форма уравнения Пуассона–Больцмана : ^{[21] : 233} $${\displaystyle \nabla ^{2}\varphi =-{\frac {\rho }{\varepsilon _{r}\varepsilon _{0}}}=-\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}.}$$

Это уравнение трудно решить, и оно не следует принципу линейной суперпозиции для связи между числом зарядов и силой потенциального поля. Оно было решено аналитически шведским математиком Томасом Хаконом Гронваллом и его коллегами физико-химиками В. К. Ла Мером и Карлом Сандведом в статье 1928 года из Physikalische Zeitschrift, посвященной расширениям теории Дебая–Хюккеля. ^[25]

Однако для достаточно низких концентраций ионов приближение разложения в ряд Тейлора первого порядка для экспоненциальной функции может быть использовано ( для ) для создания линейного дифференциального уравнения. ^{[14] : Раздел 2.4.2} D&H говорят, что это приближение справедливо при больших расстояниях между ионами, ^{[21] : 227} что то же самое, что сказать, что концентрация низкая. Наконец, они утверждают без доказательств, что добавление большего количества членов в разложение мало влияет на конечное решение. ^{[21] : 227} Таким образом ${\displaystyle e^{x}\approx 1+x}$ ${\displaystyle 0<x\ll 1}$ $${\displaystyle -\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}e^{-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}}\approx -\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}\left(1-{\frac {z_{i}q\varphi }{k_{\text{B}}T}}\right)=-\left(\sum _{i}{\frac {z_{i}qn_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}}}-\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}\varphi }{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}\right).}$$

Уравнение Пуассона–Больцмана преобразуется в ^{[21] : 233} , поскольку первая сумма равна нулю из-за электронейтральности. ^{[21] : 234} $${\displaystyle \nabla ^{2}\varphi =\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}\varphi }{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}},}$$

Вынести за скобки скалярный потенциал и присвоить остаткам, которые являются постоянными, значение . Также пусть будет ионной силой раствора: ^{[21] : 234} ${\displaystyle \kappa ^{2}}$ ${\displaystyle I}$ $${\displaystyle \kappa ^{2}=\sum _{i}{\frac {z_{i}^{2}q^{2}n_{i}^{0}}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}}={\frac {2Iq^{2}}{\varepsilon _{r}\varepsilon _{0}k_{\text{B}}T}},}$$ $${\displaystyle I={\frac {1}{2}}\sum _{i}z_{i}^{2}n_{i}^{0}.}$$

Итак, фундаментальное уравнение сводится к форме уравнения Гельмгольца : ^[26] $${\displaystyle \nabla ^{2}\varphi =\kappa ^{2}\varphi .}$$

Сегодня называется длиной экранирования Дебая . D&H в своей статье признают важность этого параметра и характеризуют его как меру толщины ионной атмосферы, которая представляет собой двойной электрический слой типа Гуи–Чепмена. ^{[21] : 229} ${\displaystyle \kappa ^{-1}}$

Уравнение можно выразить в сферических координатах , взяв некоторый произвольный ион: ^{[27] [21] : 229} ${\displaystyle r=0}$ $${\displaystyle \nabla ^{2}\varphi ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \varphi (r)}{\partial r}}\right)={\frac {\partial ^{2}\varphi (r)}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial \varphi (r)}{\partial r}}=\kappa ^{2}\varphi (r).}$$

Уравнение имеет следующее общее решение (имейте в виду, что — положительная константа): ^{[21] : 229} где , , и — неопределенные константы ${\displaystyle \kappa }$ $${\displaystyle \varphi (r)=A{\frac {e^{-{\sqrt {\kappa ^{2}}}r}}{r}}+A'{\frac {e^{{\sqrt {\kappa ^{2}}}r}}{2r{\sqrt {\kappa ^{2}}}}}=A{\frac {e^{-\kappa r}}{r}}+A''{\frac {e^{\kappa r}}{r}}=A{\frac {e^{-\kappa r}}{r}},}$$ ${\displaystyle A}$ ${\displaystyle A'}$ ${\displaystyle A''}$

Электрический потенциал равен нулю на бесконечности по определению, поэтому должен быть равен нулю. ^{[21] : 229} ${\displaystyle A''}$

На следующем этапе D&H предполагают, что существует определенный радиус , за пределами которого ни один ион в атмосфере не может приблизиться к (зарядовому) центру выделенного иона. Этот радиус может быть обусловлен физическим размером самого иона, размерами ионов в облаке и любыми молекулами воды, которые окружают ионы. Математически они рассматривают выделенный ион как точечный заряд , к которому нельзя приблизиться в пределах радиуса . ^{[21] : 231} ${\displaystyle a_{i}}$ ${\displaystyle a_{i}}$

Потенциал точечного заряда сам по себе равен $${\displaystyle \varphi _{\text{pc}}(r)={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{r}}.}$$

D&H говорят, что полный потенциал внутри сферы равен ^{[21] : 232} , где — константа, которая представляет собой потенциал, добавленный ионной атмосферой. Никакого обоснования того, что это константа, не дается. Однако можно увидеть, что это так, если учесть, что любое сферическое статическое распределение заряда подчиняется математике теоремы об оболочках . Теорема об оболочках гласит, что на заряженные частицы внутри сферы (произвольного заряда) не действует никакая сила. ^[28] Поскольку предполагается, что ионная атмосфера является (усредненной по времени) сферически симметричной, с зарядом, изменяющимся как функция радиуса , ее можно представить как бесконечную серию концентрических зарядовых оболочек. Следовательно, внутри радиуса ионная атмосфера не оказывает никакой силы. Если сила равна нулю, то потенциал является константой (по определению). $${\displaystyle \varphi _{\text{sp}}(r)=\varphi _{\text{pc}}(r)+B_{i}={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{r}}+B_{i},}$$ ${\displaystyle B_{i}}$ ${\displaystyle B_{i}}$ ${\displaystyle r}$ ${\displaystyle a_{i}}$

В сочетании непрерывно распределенной модели, которая дала уравнение Пуассона–Больцмана, и модели точечного заряда предполагается, что на радиусе имеет место непрерывность и ее первой производной. Таким образом ^{[21] : 232} ${\displaystyle a_{i}}$ ${\displaystyle \varphi (r)}$ $${\displaystyle \varphi (a_{i})=A_{i}{\frac {e^{-\kappa a_{i}}}{a_{i}}}={\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}}}+B_{i}=\varphi _{\text{sp}}(a_{i}),}$$ $${\displaystyle \varphi '(a_{i})=-{\frac {A_{i}e^{-\kappa a_{i}}(1+\kappa a_{i})}{a_{i}^{2}}}=-{\frac {1}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {z_{i}q}{a_{i}^{2}}}=\varphi _{\text{sp}}'(a_{i}),}$$ $${\displaystyle A_{i}={\frac {z_{i}q}{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {e^{\kappa a_{i}}}{1+\kappa a_{i}}},}$$ $${\displaystyle B_{i}=-{\frac {z_{i}q\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$$

По определению электрической потенциальной энергии , потенциальная энергия, связанная с выделенным ионом в ионной атмосфере, равна ^{[21] : 230 и 232} $${\displaystyle u_{i}=z_{i}qB_{i}=-{\frac {z_{i}^{2}q^{2}\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$$

Обратите внимание, что для этого требуется знать только заряд выделенного иона и потенциал всех остальных ионов.

Чтобы рассчитать потенциальную энергию всего раствора электролита, необходимо использовать обобщение множественных зарядов для электрической потенциальной энергии: ^{[21] : 230 и 232} $${\displaystyle U_{e}={\frac {1}{2}}\sum _{i=1}^{s}N_{i}u_{i}=-\sum _{i=1}^{s}{\frac {N_{i}z_{i}^{2}}{2}}{\frac {q^{2}\kappa }{4\pi \varepsilon _{r}\varepsilon _{0}}}{\frac {1}{1+\kappa a_{i}}}.}$$

Дополнительный электрический член термодинамического потенциала

Экспериментальная проверка теории

Для проверки справедливости теории Дебая-Хюккеля было испробовано много экспериментальных способов, измеряющих коэффициенты активности: проблема в том, что нам нужно идти в сторону очень высоких разбавлений. Типичные примеры: измерения давления пара, точки замерзания, осмотического давления (косвенные методы) и измерение электрического потенциала в клетках (прямой метод). При переходе к высоким разбавлениям хорошие результаты были получены с использованием ячеек с жидкой мембраной, удалось исследовать водные среды 10−4 ^M , и было обнаружено, что для электролитов 1:1 (таких как NaCl или KCl) уравнение Дебая-Хюккеля полностью верно, но для электролитов 2:2 или 3:2 можно найти отрицательное отклонение от предельного закона Дебая-Хюккеля: это странное поведение можно наблюдать только в очень разбавленной области, а в более концентрированных областях отклонение становится положительным. Возможно, что уравнение Дебая–Хюккеля не способно предсказать такое поведение из-за линеаризации уравнения Пуассона–Больцмана, а может быть и нет: исследования по этому поводу начались только в последние годы 20-го века, поскольку раньше не было возможности исследовать область 10−4 ^М , поэтому вполне возможно, что в течение следующих лет родятся новые теории.

Смотрите также

• Электролит
• Химическая активность
• Ионная сила
• Уравнение Пуассона-Больцмана
• Длина Дебая
• Длина Бьеррума
• Конвенция Бейтса-Гуггенхайма
• Ионная атмосфера
• Двойной электрический слой
• Ионная ассоциация
• Уравнение Дэвиса
• Уравнение Питцера
• Теория взаимодействия специфических ионов

Ссылки

1. П. Дебай и Э. Хюкель (1923). «Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen». Physikalische Zeitschrift . 24 : 185–206.
2. Райт, М. Р. (2007). Введение в водные растворы электролитов . Wiley. ISBN 978-0-470-84293-5.
3. Райт, раздел 1.10
4. Райт, Раздел 8.23
5. Райт, глава 10.
6. Райт, Раздел 10.3
7. Райт, Раздел 10.3
8. Райт, раздел 10.6.3
9. Райт, раздел 10.6.8.
10. Райт, раздел 10.6.10
11. Райт, раздел 10.6.15
12. Данные Райта, решенная задача 8.17
13. Райт, раздел 10.7
14. Хаманн, Хамнетт и Вилстих (1998). Электрохимия . Вайнхайм: Wiley-VCH Verlag GmbH. ISBN 3-527-29096-6.{{cite book}}: CS1 maint: multiple names: authors list (link)
15. http://homepages.rpi.edu/~keblip/THERMO/chapters/Chapter33.pdf, страница 9.
16. Райт, раздел 10.9.
17. Дэвис, CW (1962). Ионная ассоциация . Лондон: Butterworths. С. 37–53.
18. Р. Васоу, Phys. Z. , 30 (1929), 412
19. Райт, раздел 12.3
20. Райт, разделы 12.10 - 12.17
21. Собрание статей Питера Дж. В. Дебая . Нью-Йорк, Нью-Йорк: Interscience Publishers, Inc. 1954.
22. П. Дебай и Э. Хюкель (1923). «Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen». Physikalische Zeitschrift . 24 : 185–206.
23. Salzman, William R. (2001-08-21). "Смеси; Частичные молярные количества; Идеальные растворы". Химическая термодинамика . Университет Аризоны. Архивировано из оригинала 2007-06-07 . Получено 2007-10-23 .
24. http://www.pma.caltech.edu/Courses/ph136/yr2006/text.html Архивировано 28 августа 2007 г. на Wayback Machine , раздел 19.3
25. Хилле, Эйнар (1932). «Томас Хакон Гронвалл — В память». Bull. Amer. Math. Soc . 38 (11): 775–786. doi : 10.1090/s0002-9904-1932-05492-1 . MR  1562506.
26. http://guava.physics.uiuc.edu/~nigel/courses/569/Essays_2004/files/lu.pdf раздел 3.1)
27. «Уравнения Лапласа и Пуассона».
28. «Электрический потенциал заряженной сферы».