Диаграмма Смита

Графический калькулятор для инженеров-электриков

Диаграмма Смита (иногда также называемая диаграммой Смита , диаграммой Мидзухаши (水橋チャート), диаграммой Мидзухаси-Смита (水橋スミスチャート), ^{[1] [2] [3]} Диаграмма Вольперта-Смита ( Диаграмма Вольперта—Смита ) ^{[4] [ 5]} или диаграмма Мидзухаши-Вольперта-Смита ) — графический калькулятор или номограмма, предназначенная для инженеров-электриков и электронщиков, специализирующихся на радиочастотной (РЧ) технике, для помощи в решении проблем с линиями передачи и согласующими цепями. ^{[6] [7] [8] [9] [10]}

Она была независимо ^{[11] [4] [12] [5]} предложена Тосаку Мидзухаси (水橋東作) в 1937 году ^[13] и Амиэлем Р. Вольпертом  [ru] ( Амиэ́ль Р. Во́льперт ) ^{[14] [4]} и Филиппом Х. Смитом в 1939 году. ^{[15] [16]} Начав с прямоугольной диаграммы, Смит разработал специальную полярную координатную диаграмму к 1936 году, которая с участием его коллег Эноха Б. Феррелла и Джеймса У. Макрея , которые были знакомы с конформными отображениями , была переработана в окончательную форму в начале 1937 года, которая в конечном итоге была опубликована в январе 1939 года. ^{[15] [9] [17]} Хотя Смит изначально называл ее « диаграммой линий передачи » ^{[15] [16]} и другие авторы сначала использовали такие названия, как « диаграмма отражения », « круговая диаграмма импеданса ", " диаграмма иммитанса " или " диаграмма Z-плоскости ", ^[9] первые последователи в Радиационной лаборатории Массачусетского технологического института начали называть ее просто " диаграмма Смита " в 1940-х годах, ^{[9] [17]} это название стало общепринятым в западном мире к 1950 году. ^{[18] [19]}

Диаграмму Смита можно использовать для одновременного отображения нескольких параметров, включая импедансы , проводимости , коэффициенты отражения , параметры рассеяния , круги коэффициента шума , контуры постоянного усиления и области безусловной устойчивости . ^{[20] [21] : 93–103} Диаграмма Смита чаще всего используется в области радиуса единицы или внутри нее . Однако остаток по-прежнему математически актуален, например, при проектировании генераторов и анализе устойчивости . ^{[21] : 98–101} Хотя использование бумажных диаграмм Смита для решения сложных математических задач, связанных с сопоставлением, было в значительной степени заменено программными методами, диаграмма Смита по-прежнему является очень полезным методом показа ^[22] того, как параметры РЧ ведут себя на одной или нескольких частотах, альтернативой использованию табличной информации. Таким образом, большинство программ для анализа цепей РЧ включают опцию диаграммы Смита для отображения результатов, и все, кроме самых простых приборов для измерения импеданса, могут отображать результаты измерений на дисплее диаграммы Смита. ^[23] ${\displaystyle S_{nn}\,}$

Диаграмма импеданса Смита (без нанесения данных).

Обзор

Сетевой анализатор ( HP 8720A), показывающий диаграмму Смита.

Диаграмма Смита — это математическое преобразование двумерной декартовой комплексной плоскости. Комплексные числа с положительными действительными частями отображаются внутри круга. Числа с отрицательными действительными частями отображаются снаружи круга. Если мы имеем дело только с импедансами с неотрицательными резистивными компонентами, наш интерес сосредоточен на области внутри круга. Преобразование для импедансной диаграммы Смита выглядит следующим образом:

${\displaystyle \Gamma ={\frac {Z-Z_{0}}{Z+Z_{0}}}={\frac {z-1}{z+1}},}$

где т. е. комплексное сопротивление, нормализованное опорным сопротивлением, . Диаграмма Смита импеданса представляет собой диаграмму Аргана импедансов, преобразованных таким образом. Сопротивления с неотрицательными резистивными компонентами появятся внутри круга с единичным радиусом; начало координат будет соответствовать опорному сопротивлению, . ${\displaystyle z={\frac {Z}{Z_{0}}},}$ ${\displaystyle Z,}$ ${\displaystyle Z_{0}}$ ${\displaystyle Z_{0}}$

Диаграмма Смита строится на плоскости комплексного коэффициента отражения в двух измерениях и может быть масштабирована в нормализованном импедансе (наиболее распространенном), нормализованной проводимости или в обоих, используя разные цвета для их различения. Они часто известны как диаграммы Смита Z, Y и YZ соответственно. ^{[21] : 97} Нормализованное масштабирование позволяет использовать диаграмму Смита для задач, включающих любую характеристику или системный импеданс, который представлен центральной точкой диаграммы. Наиболее часто используемое нормализованное сопротивление составляет 50  Ом . После того, как ответ получен с помощью графических построений, описанных ниже, становится простым преобразование между нормализованным импедансом (или нормализованной проводимостью) и соответствующим ненормализованным значением путем умножения на характеристическое сопротивление (проводимость). Коэффициенты отражения можно считывать непосредственно с диаграммы, поскольку они являются безразмерными параметрами.

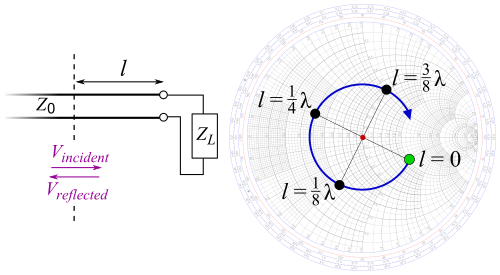
Диаграмма Смита имеет шкалу по окружности или периферии, которая градуирована в длинах волн и градусах . Шкала длин волн используется в задачах с распределенными компонентами и представляет собой расстояние, измеренное вдоль линии передачи, соединенной между генератором или источником и нагрузкой до рассматриваемой точки. Шкала градусов представляет собой угол коэффициента отражения напряжения в этой точке. Диаграмма Смита может также использоваться для задач согласования и анализа сосредоточенных элементов .

Использование диаграммы Смита и интерпретация полученных с ее помощью результатов требуют хорошего понимания теории цепей переменного тока и теории линий передачи, которые являются обязательными для инженеров по радиотехнике.

Поскольку импедансы и проводимости изменяются с частотой, проблемы с использованием диаграммы Смита можно решить только вручную, используя одну частоту за раз, а результат будет представлен точкой . Этого часто бывает достаточно для узкополосных приложений (обычно до 5–10 % полосы пропускания ), но для более широких полос пропускания обычно необходимо применять методы диаграммы Смита на более чем одной частоте в рабочей полосе частот. При условии, что частоты достаточно близки, полученные точки диаграммы Смита можно соединить прямыми линиями для создания геометрического места .

Геометрическое место точек на диаграмме Смита, охватывающее диапазон частот, можно использовать для визуального представления:

• насколько емкостной или индуктивной является нагрузка в диапазоне частот
• насколько сложным может оказаться сопоставление на разных частотах
• насколько хорошо подобран конкретный компонент.

Точность диаграммы Смита снижается для задач, включающих большую область импедансов или проводимостей, хотя масштабирование может быть увеличено для отдельных областей, чтобы учесть эти факторы.

Математическая основа

Наиболее простое использование диаграммы Смита с импедансом. Волна распространяется по линии передачи с характеристическим импедансом Z ₀ , оканчивается на нагрузке с импедансом Z _L и нормализованным импедансом z = Z _L / Z ₀ . Происходит отражение сигнала с коэффициентом Γ. Каждая точка на диаграмме Смита одновременно представляет как значение z (внизу слева), так и соответствующее значение Γ (внизу справа), связанные соотношением z = (1 + Γ)/(1 − Γ).

Фактический и нормализованный импеданс и проводимость

Линия передачи с характеристическим импедансом может универсально считаться имеющей характеристическую проводимость , где ${\displaystyle Z_{0}\,}$ ${\displaystyle Y_{0}\,}$

${\displaystyle Y_{0}={\frac {1}{Z_{0}}}\,}$

Любое сопротивление, выраженное в омах, можно нормализовать, разделив его на характеристическое сопротивление, поэтому нормализованное сопротивление с использованием строчной буквы z _T определяется по формуле ${\displaystyle Z_{\text{T}}\,}$

${\displaystyle z_{\text{T}}={\frac {Z_{\text{T}}}{Z_{0}}}\,}$

Аналогично, для нормализованного допуска

${\displaystyle y_{\text{T}}={\frac {Y_{\text{T}}}{Y_{0}}}\,}$

Единицей измерения импеданса в системе СИ является ом с символом заглавной греческой буквы омега (Ω), а единицей измерения проводимости в системе СИ является сименс с символом заглавной буквы S. Нормализованный импеданс и нормализованная проводимость являются безразмерными . Фактические импедансы и проводимости должны быть нормализованы перед использованием их на диаграмме Смита. После получения результата его можно денормализовать, чтобы получить фактический результат.

Нормализованная импедансная диаграмма Смита

Линии передачи, заканчивающиеся разомкнутой цепью (вверху) и короткозамкнутой цепью (внизу). Импульс идеально отражается от обоих этих окончаний, но знак отраженного напряжения противоположен в обоих случаях. Черные точки представляют электроны, а стрелки показывают электрическое поле.

Используя теорию линий передачи, если линия передачи заканчивается сопротивлением ( ), которое отличается от ее характеристического сопротивления ( ), на линии будет сформирована стоячая волна, включающая в себя результирующую как падающей или прямой ( ), так и отраженной или обратной ( ) волн. Используя комплексную экспоненциальную запись: ${\displaystyle Z_{\text{T}}\,}$ ${\displaystyle Z_{0}\,}$ ${\displaystyle V_{\text{F}}\,}$ ${\displaystyle V_{\text{R}}\,}$

${\displaystyle V_{\text{F}}=A\exp(j\omega t)\exp(+\gamma \ell )~\,}$и

${\displaystyle V_{\text{R}}=B\exp(j\omega t)\exp(-\gamma \ell )\,}$

где

${\displaystyle \exp(j\omega t)\,}$это временная часть волны

${\displaystyle \exp(\pm \gamma \ell )\,}$это пространственная часть волны и

${\displaystyle \omega =2\pi f\,}$где

${\displaystyle \omega \,}$угловая частота в радианах в секунду (рад/с)

${\displaystyle f\,}$частота в герцах ( Гц )

${\displaystyle t\,}$время в секундах (с)

${\displaystyle A\,}$и являются константами ${\displaystyle B\,}$

${\displaystyle \ell \,}$расстояние, измеренное вдоль линии электропередачи от нагрузки до генератора в метрах (м)

Также

${\displaystyle \gamma =\alpha +j\beta \,}$постоянная распространения , которая имеет единицы СИ радианы / метр

где

${\displaystyle \alpha \,}$постоянная затухания в неперах на метр (Нп/м)

${\displaystyle \beta \,}$фазовая постоянная в радианах на метр (рад/м)

Диаграмма Смита используется с одной частотой ( ) за раз и только для одного момента ( ) за раз, поэтому временная часть фазы ( ) фиксирована. Все члены фактически умножаются на это, чтобы получить мгновенную фазу , но это общепринято и подразумевается, чтобы опустить это. Поэтому, ${\displaystyle \omega }$ ${\displaystyle t}$ ${\displaystyle \exp(j\omega t)\,}$

${\displaystyle V_{\text{F}}=A\exp(+\gamma \ell )\,}$и

${\displaystyle V_{\text{R}}=B\exp(-\gamma \ell )\,}$

где и — соответственно амплитуды прямого и обратного напряжения на нагрузке. ${\displaystyle A\,}$ ${\displaystyle B\,}$

Изменение комплексного коэффициента отражения в зависимости от положения вдоль линии

Если смотреть на нагрузку через длинную линию передачи без потерь, то импеданс изменяется по мере увеличения, следуя синему кругу. (Этот импеданс характеризуется коэффициентом отражения .) Синий круг, расположенный в центре диаграммы Смита импеданса, иногда называют кругом КСВ (сокращение от постоянного коэффициента стоячей волны ). ${\displaystyle \ell \,}$ ${\displaystyle \ell \,}$ ${\displaystyle V_{\text{reflected}}/V_{\text{incident}}}$

Комплексный коэффициент отражения напряжения определяется как отношение отраженной волны к падающей (или прямой) волне. Таким образом, ${\displaystyle \Gamma \,}$

${\displaystyle \Gamma ={\frac {V_{\text{R}}}{V_{\text{F}}}}={\frac {B\exp(-\gamma \ell )}{A\exp(+\gamma \ell )}}=C\exp(-2\gamma \ell )\,}$

где C также является константой.

Для однородной линии передачи (в которой есть константа) комплексный коэффициент отражения стоячей волны изменяется в зависимости от положения на линии. Если линия имеет потери ( не равно нулю), это представлено на диаграмме Смита спиральной траекторией . Однако в большинстве задач диаграммы Смита потери можно считать пренебрежимо малыми ( ), и задача их решения значительно упрощается. Поэтому для случая без потерь выражение для комплексного коэффициента отражения становится ${\displaystyle \gamma \,}$ ${\displaystyle \alpha \,}$ ${\displaystyle \alpha =0\,}$

${\displaystyle \Gamma =\Gamma _{\text{L}}\exp(-2j\beta \ell )\,}$

где - коэффициент отражения на нагрузке, а - длина линии от нагрузки до места, где измеряется коэффициент отражения. Фазовая константа может быть также записана как ${\displaystyle \Gamma _{\text{L}}\,}$ ${\displaystyle \ell \,}$ ${\displaystyle \beta \,}$

${\displaystyle \beta ={\frac {2\pi }{\lambda }}\,}$

где — длина волны в линии передачи на тестовой частоте. ${\displaystyle \lambda \,}$

Поэтому,

${\displaystyle \Gamma =\Gamma _{\text{L}}\exp \left({\frac {-4j\pi }{\lambda }}\ell \right)\,}$

Это уравнение показывает, что для стоячей волны комплексный коэффициент отражения и импеданс повторяются каждые полдлины волны вдоль линии передачи. Комплексный коэффициент отражения обычно просто называют коэффициентом отражения. Внешняя окружная шкала диаграммы Смита представляет расстояние от генератора до нагрузки, масштабированное в длинах волн, и поэтому масштабируется от нуля до 0,50.

Изменение нормализованного импеданса в зависимости от положения вдоль линии

Если и — напряжение на конце линии передачи и ток, поступающий на ее оконечное устройство, соответственно, то ${\displaystyle \,V\,}$ ${\displaystyle \,I\,}$

${\displaystyle V_{\mathsf {F}}+V_{\mathsf {R}}=V\,}$

и

${\displaystyle V_{\mathsf {F}}-V_{\mathsf {R}}=Z_{0}\,I\,}$.

Разделив эти уравнения и подставив вместо них коэффициент отражения напряжения

${\displaystyle \Gamma ={\frac {V_{\mathsf {R}}}{\,V_{\mathsf {F}}\,}}\,}$

и нормализованный импеданс окончания, представленный строчной буквой z , нижним индексом T

${\displaystyle z_{\mathsf {T}}={\frac {V}{\,Z_{0}\,I\,}}\,}$

дает результат:

${\displaystyle z_{\mathsf {T}}={\frac {1+\Gamma }{\,1-\Gamma \,}}\,.}$

Альтернативно, с точки зрения коэффициента отражения

${\displaystyle \Gamma ={\frac {z_{\mathsf {T}}-1}{\,z_{\mathsf {T}}+1\,}}\,}$

Это уравнения, которые используются для построения Z -диаграммы Смита. Математически они связаны через преобразование Мёбиуса . ${\displaystyle \,\Gamma \,}$ ${\displaystyle \,z_{\mathsf {T}}\,}$

Оба и выражаются в комплексных числах без каких-либо единиц измерения. Они оба изменяются с частотой, поэтому для любого конкретного измерения частота, на которой оно было выполнено, должна быть указана вместе с характеристическим импедансом. ${\displaystyle \,\Gamma \,}$ ${\displaystyle \,z_{\mathsf {T}}\,}$

${\displaystyle \,\Gamma \,}$может быть выражено в виде величины и угла на полярной диаграмме . Любой фактический коэффициент отражения должен иметь величину, меньшую или равную единице , поэтому на тестовой частоте это может быть выражено точкой внутри круга с радиусом единицы. Диаграмма Смита фактически построена на такой полярной диаграмме. Масштабирование диаграммы Смита разработано таким образом, что коэффициент отражения может быть преобразован в нормализованный импеданс или наоборот. Используя диаграмму Смита, нормализованный импеданс может быть получен с заметной точностью путем нанесения точки, представляющей коэффициент отражения, рассматривая диаграмму Смита как полярную диаграмму , а затем считывая ее значение напрямую с помощью характеристического масштабирования диаграммы Смита. Этот метод является графической альтернативой подстановке значений в уравнения.

Подставляя выражение для изменения коэффициента отражения вдоль несогласованной линии передачи без потерь

${\displaystyle \Gamma ={\frac {B\exp(-\gamma \ell )}{A\exp(\gamma \ell )}}={\frac {B\exp(-j\beta \ell )}{A\exp(j\beta \ell )}}\,}$

для случая без потерь — в уравнение для нормализованного импеданса в терминах коэффициента отражения

${\displaystyle z_{\mathsf {T}}={\frac {1+\Gamma }{\,1-\Gamma \,}}\,.}$

и используя формулу Эйлера

${\displaystyle \exp(j\theta )={\text{cis}}\,\theta =\cos \theta +j\,\sin \theta \,}$

дает уравнение линии передачи в версии импеданса для случая без потерь: ^[24]

${\displaystyle Z_{\mathsf {in}}=Z_{0}{\frac {\,Z_{\mathsf {L}}+j\,Z_{0}\tan(\beta \ell )\,}{\,Z_{0}+j\,Z_{\mathsf {L}}\tan(\beta \ell )\,}}\,}$

где - импеданс, «видимый» на входе линии передачи без потерь длиной, нагруженной импедансом ${\displaystyle \,Z_{\mathsf {in}}\,}$ ${\displaystyle \,\ell \,,}$ ${\displaystyle \,Z_{\mathsf {L}}\,}$

Аналогичным образом можно вывести варианты уравнения линии передачи для случая без потерь проводимости и для случаев с потерями импеданса и проводимости.

Графический эквивалент использования уравнения линии передачи для диаграммы Смита заключается в нормализации для построения результирующей точки на диаграмме Смита Z и проведении окружности через эту точку с центром в центре диаграммы Смита. Путь вдоль дуги окружности показывает, как изменяется импеданс при движении вдоль линии передачи. В этом случае необходимо использовать окружное (длина волны) масштабирование, помня, что это длина волны внутри линии передачи, и она может отличаться от длины волны в свободном пространстве. ${\displaystyle \,Z_{\mathsf {L}}\,,}$

РегионыЗДиаграмма Смита

Если полярная диаграмма отображается в декартовой системе координат , то принято измерять углы относительно положительной оси x , используя направление против часовой стрелки для положительных углов. Величина комплексного числа — это длина прямой линии, проведенной из начала координат в точку, представляющую его. Диаграмма Смита использует то же соглашение, отмечая, что в нормализованной плоскости импеданса положительная ось x простирается от центра диаграммы Смита в до точки Область над осью x представляет индуктивные импедансы (положительные мнимые части), а область под осью x представляет емкостные импедансы (отрицательные мнимые части). ${\displaystyle \,z_{\mathsf {T}}=1\pm j0\,}$ ${\displaystyle \,z_{\mathsf {T}}=\infty \pm j\infty \,.}$

Если окончание идеально согласовано, коэффициент отражения будет равен нулю, эффективно представленный окружностью нулевого радиуса или фактически точкой в ​​центре диаграммы Смита. Если окончание было идеальной разомкнутой цепью или коротким замыканием, величина коэффициента отражения будет равна единице, вся мощность будет отражена, а точка будет лежать в некоторой точке на окружности единичной окружности.

Круги постоянного нормализованного сопротивления и постоянного нормализованного реактивного сопротивления

Нормализованная диаграмма Смита импеданса состоит из двух семейств окружностей: окружностей постоянного нормализованного сопротивления и окружностей постоянного нормализованного реактивного сопротивления. В комплексной плоскости коэффициента отражения диаграмма Смита занимает окружность единичного радиуса с центром в начале координат. В декартовых координатах окружность, таким образом, проходила бы через точки (+1,0) и (−1,0) на оси x и точки (0,+1) и (0,−1) на оси y .

Поскольку и являются комплексными числами, в общем случае их можно записать как: ${\displaystyle \,\Gamma \,}$ ${\displaystyle \,z_{\mathsf {T}}\,}$

${\displaystyle z_{\mathsf {T}}=a+jb\,}$

${\displaystyle ~\Gamma ~=c+jd\,}$

с действительными числами a , b , c и d .

Подставим их в уравнение, связывающее нормализованный импеданс и комплексный коэффициент отражения:

${\displaystyle \Gamma ={\frac {z_{\mathsf {T}}-1}{\,z_{\mathsf {T}}+1\,}}={\frac {(a-1)+j\,b}{\,(a+1)+j\,b\,}}\,}$

дает следующий результат:

${\displaystyle \Gamma =c+jd=\left[{\frac {a^{2}+b^{2}-1}{\,(a+1)^{2}+b^{2}\,}}\right]+j\left[{\frac {2b}{\,(a+1)^{2}+b^{2}\,}}\right]=\left[1+{\frac {-2(a+1)}{\,(a+1)^{2}+b^{2}\,}}\right]+j\left[{\frac {+2b}{\,(a+1)^{2}+b^{2}\,}}\right]\,.}$

Это уравнение описывает, как комплексный коэффициент отражения изменяется в зависимости от нормализованного импеданса, и может быть использовано для построения обоих семейств окружностей. ^[25]

TheИДиаграмма Смита

Диаграмма Смита Y строится аналогично диаграмме Смита Z , но выражая значения коэффициента отражения напряжения в терминах нормализованной проводимости вместо нормализованного импеданса. Нормализованная проводимость y _T является обратной величиной нормализованного импеданса z _T , поэтому

${\displaystyle y_{\mathsf {T}}={\frac {1}{z_{\mathsf {T}}}}\,}$

Поэтому:

${\displaystyle y_{\mathsf {T}}={\frac {1-\Gamma }{\,1+\Gamma \,}}\,}$

и

${\displaystyle \Gamma ={\frac {1-y_{\mathsf {T}}}{\,1+y_{\mathsf {T}}\,}}\,}$

Диаграмма Y -Смита выглядит так же, как и нормализованный тип импеданса, но с графическими вложенными кругами, повернутыми на 180°, а числовая шкала остается в том же положении (не повернута), что и диаграмма Z.

Аналогично принимая

${\displaystyle y_{\mathsf {T}}={\tilde {o}}+j\,{\tilde {p}}\,}$

для реального и дает аналогичный результат, хотя с большим количеством и другими знаками минус: ${\displaystyle \,{\tilde {o}}\,}$ ${\displaystyle \,{\tilde {p}}\,}$

${\displaystyle \Gamma =c+jd=\left[{\frac {1-{\tilde {o}}^{2}-{\tilde {p}}^{2}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]+j\left[{\frac {-2{\tilde {p}}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]=\left[{\frac {2({\tilde {o}}+1)}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}-1\right]+j\left[{\frac {-2{\tilde {p}}}{\,({\tilde {o}}+1)^{2}+{\tilde {p}}^{2}\,}}\right]\,.}$

Область выше оси x представляет емкостные проводимости, а область ниже оси x представляет индуктивные проводимости. Емкостные проводимости имеют положительные мнимые части, а индуктивные проводимости имеют отрицательные мнимые части.

Опять же, если окончание идеально согласовано, коэффициент отражения будет равен нулю, представленному «кругом» нулевого радиуса или фактически точкой в ​​центре диаграммы Смита. Если бы окончание было идеальным разомкнутым или коротким замыканием, величина коэффициента отражения напряжения была бы равна единице, вся мощность была бы отражена, и точка лежала бы в некоторой точке на окружности единичной окружности диаграммы Смита.

Практические примеры

Примеры точек, нанесенных на нормализованную диаграмму импеданса Смита.

Точка с коэффициентом отражения величиной 0,63 и углом 60°, представленная в полярной форме как , показана как точка P ₁ на диаграмме Смита. Чтобы построить ее, можно использовать шкалу окружных (коэффициента отражения) углов, чтобы найти градуировку , и линейку, чтобы нарисовать линию, проходящую через нее и центр диаграммы Смита. Длина линии затем будет масштабирована до P _1, предполагая, что радиус диаграммы Смита равен единице. Например, если фактический радиус, измеренный с бумаги, составляет 100 мм, длина OP ₁ будет равна 63 мм. ${\displaystyle 0.63\angle 60^{\circ }\,}$ ${\displaystyle \angle 60^{\circ }\,}$

В следующей таблице приведены некоторые похожие примеры точек, нанесенных на диаграмму Смита Z. Для каждой из них коэффициент отражения дан в полярной форме вместе с соответствующим нормализованным импедансом в прямоугольной форме. Преобразование можно прочитать непосредственно из диаграммы Смита или путем подстановки в уравнение.

Работая с обоимиЗДиаграмма Смита иИДиаграммы Смита

В задачах СВЧ-цепей и согласования иногда удобнее работать с проводимостями (представляющими проводимости и реактивности ), а иногда удобнее работать с импедансами (представляющими сопротивления и реактивности ). Решение типичной задачи согласования часто требует нескольких изменений между обоими типами диаграммы Смита, используя нормализованный импеданс для последовательных элементов и нормализованные проводимости для параллельных элементов. Для них может использоваться двойная (нормализованная) диаграмма Смита импеданса и проводимости. В качестве альтернативы можно использовать один тип и при необходимости преобразовывать масштабирование в другой. Чтобы перейти от нормализованного импеданса к нормализованной проводимости или наоборот, точка, представляющая значение рассматриваемого коэффициента отражения, перемещается точно на 180 градусов по тому же радиусу. Например, точка P1 в примере, представляющая коэффициент отражения, имеет нормализованный импеданс . Чтобы графически изменить это на эквивалентную нормализованную точку проводимости, скажем, Q1, линейкой проводится линия от P1 через центр диаграммы Смита до Q1, равный радиус в противоположном направлении. Это эквивалентно перемещению точки по круговой траектории ровно на 180 градусов. Считывание значения с диаграммы Смита для Q1, помня, что масштабирование теперь находится в нормализованной проводимости, дает . Выполнение расчета ${\displaystyle 0.63\angle 60^{\circ }\,}$ ${\displaystyle z_{P}=0.80+j1.40\,}$ ${\displaystyle y_{P}=0.30-j0.54\,}$

${\displaystyle y_{\text{T}}={\frac {1}{z_{\text{T}}}}\,}$

вручную подтвердит это.

После выполнения преобразования импеданса в проводимость масштабирование изменяется на нормализованную проводимость до тех пор, пока не будет выполнено последующее преобразование обратно в нормализованный импеданс.

В таблице ниже показаны примеры нормализованных импедансов и их эквивалентных нормализованных проводимостей, полученных вращением точки на 180°. Опять же, их можно получить либо расчетом, либо с помощью диаграммы Смита, как показано, преобразуя между плоскостями нормализованного импеданса и нормализованных проводимостей.

Значения комплексного коэффициента отражения, нанесенные на диаграмму Смита нормализованного импеданса, и их эквиваленты на диаграмму Смита нормализованной адмиттанса.

Выбор типа диаграммы Смита и типа компонента

Выбор между диаграммой Смита Z или диаграммой Смита Y для любого конкретного расчета зависит от того, что удобнее. Последовательные импедансы и параллельные проводимости складываются, в то время как параллельные импедансы и последовательные проводимости связаны обратным уравнением. Если — эквивалентное сопротивление последовательных импедансов, а — эквивалентное сопротивление параллельных импедансов, то ${\displaystyle Z_{\text{TS}}}$ ${\displaystyle Z_{\text{TP}}}$

${\displaystyle Z_{\text{TS}}=Z_{1}+Z_{2}+Z_{3}+...\,}$

${\displaystyle {\frac {1}{Z_{\text{TP}}}}={\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}+{\frac {1}{Z_{3}}}+...\,}$

Для допусков верно обратное, то есть

${\displaystyle Y_{\text{TP}}=Y_{1}+Y_{2}+Y_{3}+...\,}$

${\displaystyle {\frac {1}{Y_{\text{TS}}}}={\frac {1}{Y_{1}}}+{\frac {1}{Y_{2}}}+{\frac {1}{Y_{3}}}+...\,}$

Работа с обратными величинами , особенно в комплексных числах, требует больше времени и подвержена ошибкам, чем использование линейного сложения. Поэтому, как правило, большинство инженеров по радиочастотам работают в плоскости, где топография схемы поддерживает линейное сложение. В следующей таблице приведены комплексные выражения для импеданса (действительного и нормализованного) и проводимости (действительной и нормализованной) для каждого из трех основных пассивных элементов схемы : сопротивления, индуктивности и емкости. Используя только характеристический импеданс (или характеристическую проводимость) и тестовую частоту, можно найти эквивалентную схему и наоборот.

Использование диаграммы Смита для решения задач сопряженного соответствия с распределенными компонентами

Распределенное согласование становится возможным и иногда требуется, когда физический размер согласующих компонентов составляет более 5% длины волны на рабочей частоте. Здесь электрическое поведение многих сосредоточенных компонентов становится довольно непредсказуемым. Это происходит в микроволновых цепях и когда высокая мощность требует больших компонентов в коротковолновом, FM и телевизионном вещании.

Для распределенных компонентов необходимо учитывать влияние перемещения вдоль линии передачи на коэффициент отражения и импеданс, используя внешнюю окружную шкалу диаграммы Смита, откалиброванную в длинах волн.

Следующий пример показывает, как линия передачи, нагруженная произвольной нагрузкой, может быть согласована на одной частоте с последовательным или параллельным реактивным компонентом, в каждом случае подключенным в точных положениях.

Построение диаграммы Смита для согласования некоторых распределенных линий передачи.

Предположим, что линия передачи без потерь с воздушным зазором и характеристическим импедансом , работающая на частоте 800 МГц, заканчивается цепью, состоящей из резистора 17,5 Ом последовательно с катушкой индуктивности 6,5 наногенри (6,5 нГн). Как можно согласовать линию? ${\displaystyle Z_{0}=50\ \Omega }$ ${\displaystyle \Omega }$

Из приведенной выше таблицы следует, что реактивное сопротивление индуктора, входящего в состав окончания на частоте 800 МГц, равно

${\displaystyle Z_{L}=j\omega L=j2\pi fL=j32.7\ \Omega \,}$

поэтому импеданс комбинации ( ) определяется как ${\displaystyle Z_{T}}$

${\displaystyle Z_{T}=17.5+j32.7\ \Omega \,}$

и нормализованный импеданс ( ) равен ${\displaystyle z_{T}}$

${\displaystyle z_{T}={\frac {Z_{T}}{Z_{0}}}=0.35+j0.65\,}$

Это отображено на диаграмме Смита Z в точке P ₂₀ . Линия OP ₂₀ продолжается до шкалы длин волн, где она пересекается в точке . Поскольку линия передачи не имеет потерь, окружность с центром в центре диаграммы Смита проведена через точку P ₂₀ для представления пути коэффициента отражения постоянной величины из-за окончания. В точке P ₂₁ окружность пересекается с окружностью единицы постоянного нормализованного сопротивления в ${\displaystyle L_{1}=0.098\lambda \,}$

${\displaystyle z_{P21}=1.00+j1.52\,}$.

Продолжение линии OP ₂₁ пересекает шкалу длин волн в точке , поэтому расстояние от окончания до этой точки на линии определяется выражением ${\displaystyle L_{2}=0.177\lambda \,}$

${\displaystyle L_{2}-L_{1}=0.177\lambda -0.098\lambda =0.079\lambda \,}$

Поскольку линия передачи расположена в воздушном пространстве, длина волны на частоте 800 МГц в линии такая же, как и в свободном пространстве, и определяется по формуле

${\displaystyle \lambda ={\frac {c}{f}}\,}$

где - скорость электромагнитного излучения в свободном пространстве , а - частота в герцах. Результат дает , что делает положение согласующего компонента 29,6 мм от нагрузки. ${\displaystyle c\,}$ ${\displaystyle f\,}$ ${\displaystyle \lambda =375\ \mathrm {mm} \,}$

Сопряженное соответствие для импеданса в точке P ₂₁ ( ) равно ${\displaystyle z_{match}\,}$

${\displaystyle z_{match}=-j(1.52),\!}$

Поскольку диаграмма Смита по-прежнему находится в плоскости нормализованного импеданса, из приведенной выше таблицы следует, что последовательный конденсатор требуется там, где ${\displaystyle C_{m}\,}$

${\displaystyle z_{match}=-j1.52={\frac {-j}{\omega C_{m}Z_{0}}}={\frac {-j}{2\pi fC_{m}Z_{0}}}\,}$

Переставляя, получаем

${\displaystyle C_{m}={\frac {1}{(1.52)\omega Z_{0}}}={\frac {1}{(1.52)(2\pi f)Z_{0}}}}$.

Подстановка известных значений дает

${\displaystyle C_{m}=2.6\ \mathrm {pF} \,}$

Для согласования с нагрузкой на частоте 800 МГц необходимо последовательно с линией передачи на расстоянии 29,6 мм от нагрузки включить конденсатор емкостью 2,6 пФ.

Альтернативное соответствие шунта может быть рассчитано после выполнения преобразования диаграммы Смита из нормализованного импеданса в нормализованную проводимость. Точка Q ₂₀ эквивалентна P ₂₀ , но выражена как нормализованная проводимость. Считывание из масштабирования диаграммы Смита, помня, что теперь это нормализованная проводимость, дает

${\displaystyle y_{Q20}=0.65-j1.20\,}$

(На самом деле это значение фактически не используется). Однако, расширение линии OQ ₂₀ до шкалы длин волн дает . Самая ранняя точка, в которой может быть введено сопряженное шунтирующее соответствие, двигаясь к генератору, будет в Q ₂₁ , то же положение, что и предыдущее P ₂₁ , но на этот раз представляющее нормализованную проводимость, заданную ${\displaystyle L_{3}=0.152\lambda \,}$

${\displaystyle y_{Q21}=1.00+j1.52\,}$.

Расстояние вдоль линии электропередачи в этом случае равно

${\displaystyle L_{2}+L_{3}=0.177\lambda +0.152\lambda =0.329\lambda \,}$

что преобразуется в 123 мм.

Сопряженный компонент соответствия должен иметь нормализованную проводимость ( ) ${\displaystyle y_{match}}$

${\displaystyle y_{match}=-j1.52\,}$.

Из таблицы видно, что отрицательная проводимость потребует катушки индуктивности, подключенной параллельно линии передачи. Если ее значение равно , то ${\displaystyle L_{m}\,}$

${\displaystyle -j1.52={\frac {-j}{\omega L_{m}Y_{0}}}={\frac {-jZ_{0}}{2\pi fL_{m}}}\,}$

Это дает результат

${\displaystyle L_{m}=6.5\ \mathrm {nH} \,}$

Подходящим согласующим индуктивным шунтом будет, таким образом, катушка индуктивности 6,5 нГн, включенная параллельно линии и расположенная на расстоянии 123 мм от нагрузки.

Использование диаграммы Смита для анализа цепей с сосредоточенными элементами

Анализ компонентов с сосредоточенными элементами предполагает, что длина волны на рабочей частоте намного больше размеров самих компонентов. Диаграмма Смита может использоваться для анализа таких цепей, в этом случае движения вокруг диаграммы генерируются (нормализованными) импедансами и проводимостями компонентов на рабочей частоте. В этом случае масштабирование длины волны на окружности диаграммы Смита не используется. Следующая схема будет проанализирована с использованием диаграммы Смита на рабочей частоте 100 МГц. На этой частоте длина волны в свободном пространстве составляет 3 м. Размеры самих компонентов будут порядка миллиметров, поэтому предположение о сосредоточенных компонентах будет действительным. Несмотря на отсутствие линии передачи как таковой, системное сопротивление все равно должно быть определено для обеспечения возможности расчетов нормализации и денормализации, и здесь это хороший выбор, поскольку . Если бы присутствовали очень разные значения сопротивления, то значение, более близкое к ним, могло бы быть лучшим выбором. ${\displaystyle Z_{0}=50\ \Omega \,}$ ${\displaystyle R_{1}=50\ \Omega \,}$

Схема с сосредоточенными элементами, которую можно проанализировать с помощью диаграммы Смита.

Диаграмма Смита с графическим построением для анализа сосредоточенной цепи.

Анализ начинается с диаграммы Смита Z, которая рассматривает только R ₁ без других компонентов. Как и импеданс системы, это представлено точкой в ​​центре диаграммы Смита. Первое преобразование - OP ₁ вдоль линии постоянного нормализованного сопротивления, в данном случае добавление нормализованного реактивного сопротивления - j 0,80, что соответствует последовательному конденсатору емкостью 40 пФ. Точки с суффиксом P находятся в плоскости Z , а точки с суффиксом Q находятся в плоскости Y. Таким образом, преобразования P ₁ в Q ₁ и P ₃ в Q ₃ происходят из диаграммы Смита Z в диаграмму Смита Y, а преобразование Q ₂ в P ₂ происходит из диаграммы Смита Y в диаграмму Смита Z. В следующей таблице показаны шаги, предпринятые для работы с оставшимися компонентами и преобразованиями, в конечном итоге возвращаясь обратно в центр диаграммы Смита и к идеальному соответствию 50 Ом. ${\displaystyle R_{1}=50\ \Omega \,}$

3D-диаграмма Смита

Трехмерное представление диаграммы Смита.

Обобщение диаграммы Смита на трехмерную сферу, основанное на расширенной комплексной плоскости ( сфере Римана ) и инверсной геометрии , было предложено Мюллером и др. в 2011 году. ^[26]

Схема объединяет пассивную и активную схему проектирования на малых и больших кругах на поверхности единичной сферы, используя стереографическую конформную карту обобщенной плоскости коэффициента отражения. Рассматривая точку на бесконечности, пространство новой схемы включает все возможные нагрузки: Северный полюс является идеально согласованной точкой, в то время как южный полюс является полностью несогласованной точкой. ^[26]

Трехмерная диаграмма Смита была расширена за пределы сферической поверхности для построения различных скалярных параметров, таких как групповая задержка, добротности или ориентация частоты. Визуальная ориентация частоты (по часовой стрелке или против часовой стрелки) позволяет различать отрицательную/емкостную и положительную/индуктивную, коэффициенты отражения которых одинаковы при построении на двухмерной диаграмме Смита, но ориентация которых расходится с увеличением частоты. ^[27]

Смотрите также

• Бинарная мозаика
• Участок Боде
• График Найквиста
• Круговая диаграмма Хейланда–Осанны
• цис (математика)
• Трансверсальный (приборостроение)

Ссылки

1. Окамура [岡村], Фумиёси [史良] / Широ [獅郎] (август 1959 г.) [1959-04-04]. «Sumisuchāto wa nihonjin no dokusōde wanai ka» スミスチャートは日本人の独創ではないか [«Диаграмма Смита» может иметь происхождение из Японии] (PDF) . Журнал Института инженеров электросвязи Японии [電気通信学会雑誌] (на японском языке). 1959 (8). Токио, Япония: Институт инженеров электросвязи Японии [電気通信学会]: 768–769 (44–45). ISSN  0914-5273. Архивировано из оригинала (PDF) 16 ноября 2017 г.(2 страницы) (Примечание. В статье имя автора указано как史良на японском языке, что переводится как «Фумиёси», тогда как в английской сноске в той же статье оно транскрибировано как «Сиро», что на японском языке ассоциируется с獅郎.)
2. Кеничи [伊藤健], Ито [一著] (1 ноября 1999 г.). Инпидансу но ханаси インピーダンスのはなし[ История импеданса ]. Наука и технологии (на японском языке) (1-е изд.). Никкан Когё Симбун [日刊工業新聞社]. п. 26. ISBN 4-526-04463-6. EAN  978-4-526-04463-2. 1923054018007.(4+xi+1+207+3+4 страницы)
3. Мори [森], Кунихико [邦彦] (2013). «Диаграмма Мизухаси-Смита». morikuni_net . Архивировано из оригинала 3 марта 2013 г. Проверено 24 июня 2023 г.
4. Курочкин [Курочкин], Александр Евдокимович [Александр Евдокимович] (2009). «Диаграмма Вольперта – Смита. Расчет и анализ характеристик усилителей радиосигналов» Диаграмма Вольперта – Смита. Расчет и анализ характеристик усилителей радиосигналов. Расчет и анализ характеристик усилителей радиосигналов] (PDF) (на русском языке). Минск, Беларусь: Кафедра «Радиотехнические устройства», Белорусский государственный университет информатики и радиоэлектроники, образовательное учреждение Министерства образования Республики Беларусь. ISBN 978-9-85-488-422-6. Архивировано (PDF) из оригинала 9 июля 2023 г. Проверено 9 июля 2023 г. п. 4: Схема Смита остается одним из наиболее полезных графических инструментов для разработки высокочастотных усилительных каскадов. В нашей стране аналогичная диаграмма известна как круговая номограмма А. Р. Вольперта, который в 1939 г. независимо от Смита разработал и применил ее для пересчета проводимостей и сопротивлений в отрезках линий передачи. Диаграмма Смита остается одним из наиболее полезных графических инструментов для разработки высокочастотных преобразователей каскадов. В нашей стране аналогичная диаграмма осталась как круговая номограмма А. Р. Вольперта, который в 1939 г. Независимо от Смита разработал и применил ее для пересчета проводимостей и сопротивлений в отрезках линий передачи.[В нашей стране подобная диаграмма известна как круговая номограмма А.Р. Вольперта, который в 1939 году независимо от Смита разработал и применил ее для пересчета проводимостей и сопротивлений на участках линий электропередачи.][1][2][3] (40+1 страниц)
5. Салов, Михаил (март 2022 г.). "4. Диаграмма Вольперта–Смита". Измерение и согласование импеданса антенн (PDF) (прикладная заметка). Texas Instruments . стр. 11. SWRA726. Архивировано (PDF) из оригинала 2023-06-26 . Получено 2023-06-26 .(51 страница)
6. Рамо, Саймон «Си» ; Уиннери, Джон Рой ; Ван Дузер, Теодор (1965). Поля и волны в коммуникационной электронике (1-е изд.). John Wiley & Sons . стр. 35–39.
7. Рамо, Саймон "Си" ; Уиннери, Джон Рой ; Ван Дузер, Теодор (1994). "5.9. Схема линий передачи Смита / 5.10. Некоторые применения схемы Смита". Поля и волны в коммуникационной электронике (3-е изд.). John Wiley & Sons, Inc. стр. 236–245. ISBN 978-0-471-58551-0.
8. Смит, Филлип Хагар (июнь 1969). Написано в Пайн-Брук, Нью-Джерси, США. Электронные приложения диаграммы Смита: в волноводном, схемном и компонентном анализе (1-е изд.). Нью-Йорк, США: McGraw-Hill Book Company / Kay Electric Company. ISBN 0-07058930-5. LCCN  69-12411. ISBN 978-0-07058930-8 . (xxvii+1+222 страницы + конверт с 4 полупрозрачными пластиковыми накладками + почтовая открытка Kay Electric Company) (Примечание. Существует переиздание 1983 года первого издания издательством Robert E. Krieger Publishing Company с ISBN 978-0-89874-552-8 , 0-89874-552-7 , а также второе издание издательством Noble Publishing Corporation.) 
9. Smith, Phillip Hagar (октябрь 2000 г.) [1995]. Электронные приложения диаграммы Смита: в анализе волноводов, цепей и компонентов (2-е изд.). Атланта, Джорджия, США: Noble Publishing Corporation . ISBN 1-884932-39-8. LCCN  00-045239. ISBN 978-1-884932-39-7 . стр. xiv: […] Из уравнения Флеминга [ ^A] и в попытке упростить решение проблемы линии передачи он разработал свое первое графическое решение в виде прямоугольного графика. […] диаграмма постепенно развивалась через ряд шагов. Первая прямоугольная диаграмма была ограничена диапазоном данных, которые она могла вместить. Он знал об ограничениях и продолжал работать над проблемой до некоторого времени в 1936 году, когда он разработал новую диаграмму, которая устранила большинство трудностей. Новая диаграмма представляла собой специальную форму полярных координат , в которой могли быть размещены все значения компонентов импеданса. Данные для этой диаграммы были масштабированы из более ранней прямоугольной диаграммы. Координаты импеданса в этом случае не были ортогональны и не были истинными окружностями, но в выбранной форме отношение стоячей волны было линейным. Диаграмма очень напоминала то, что в конечном итоге стало конечным результатом. Фил , однако, подозревал, что сетка, составленная из системы ортогональных окружностей, может быть более практичной. Он чувствовал, что она будет иметь определенные преимущества, особенно в отношении воспроизводимости. Имея это в виду, он поговорил с двумя своими коллегами, Э. Б. Ферреллом и Дж. В. Макреем . Поскольку они были знакомы с принципами конформного отображения , они смогли разработать преобразование, с помощью которого можно было бы разместить все данные от нуля до бесконечности. К счастью, кривые постоянного коэффициента стоячей волны, постоянного затухания и постоянного коэффициента отражения были все кругами, соосными с центром диаграммы. Шкалы для этих значений, хотя и не линейные, были полностью удовлетворительными. Диаграмма, разработанная по этим линиям, была построена в начале 1937 года. По сути, это была форма, которая используется и сегодня. Смит обратился в ряд технических журналов с просьбой опубликовать диаграмму, но принятие было медленным. В то время было не так много технических журналов, и ни один из них не был посвящен микроволновому излучению. Однако в январе 1939 года, с опозданием в два года, статья была напечатана в журнале Electronics . […] (xxvi+237+1 страниц + конверт с 4 полупрозрачными пластиковыми накладками) (Примечание. Существует переиздание второго издания 2006 года издательством SciTech Publishing, Inc. под теми же ISBN и LCCN.)
10. "Соответствие импеданса и импеданс диаграммы Смита" (прикладная заметка). Maxim Integrated Products, Inc. 2012 [2002-07-22]. Учебник 742. Архивировано из оригинала 2023-07-09 . Получено 2023-07-09 .[4] (18 страниц) (Примечание. Предыдущая версия этой статьи была опубликована в июльском номере журнала RF Design за 2000 год .)
11. Voltmer, David (2007-08-17). "8.2. The Smith Chart". В Balanis, Constantine A. (ред.). Fundamentals Of Electromagnetics 2. Quasistatics And Waves. Synthesis Lectures On Computational Electromagnetics. Том 2 (1-е изд.). Morgan & Claypool . стр. 135–141 [135]. doi :10.2200/S00078ED1V01Y200612CEM015. ISBN 978-1-59829172-8. ISSN  1932-1716. S2CID  9045052. ISBN 1-59829172-6 . LoC 1932-1252. MOBK081-FM . Получено 25.06.2023 . стр. 135: Хотя Вольперт из Советского Союза и Мизухаси из Японии предложили по сути одну и ту же диаграмму в один и тот же год, признание получил Смит. 
12. "Smith Chart". ETHW.org . 2018-02-26. Архивировано из оригинала 2023-07-08 . Получено 2021-03-30 .
13. Мизухаси [水橋], Тосаку [東作] (декабрь 1937 г.) [1937-11-19]. «Sì duānzϐ huílù no inpīdansu hensei to seigō kairo no riron» 四端子回路のインピーダンス変成と整合回路の理論 [Теория четырехполюсной схемы преобразования импеданса и согласующая схема] (PDF) . Журнал Института инженеров электросвязи Японии [電気通信学会雑誌] (на японском языке). 1937 (12). Институт инженеров электросвязи Японии [電気通信学会]: 1053–1058 (29–34). ISSN  0914-5273. Архивировано из оригинала (PDF) 16 ноября 2017 г.(6 страниц)
14. Вольперт [Во́льперт], Амиэль Рафаилович [Амиэль Рафаилович] [на русском языке] (февраль 1940 г.). «Номограмма для расчета длинных линий».Номограмма для расчета линий[Номограмма для расчета длинных линий]. Производственно-технический бюллетень (Производственно-технический бюллетень ). Том. 1940, нет. 2. Ленинград , СССР: НКЭП  [ru] . стр. 14–18.(5 страниц)
15. Smith, Phillip Hagar (январь 1939). "Калькулятор линии передачи - "вырезной" калькулятор для определения импеданса и затухания в терминах длины открытых линий передачи" (PDF) . электроника - радио, связь, промышленное применение электронных ламп ... проектирование и производство . Том 12, № 1. Нью-Йорк, США: McGraw-Hill Publishing Company, Inc. стр. 29–31. ISSN  0013-5070. Архивировано (PDF) из оригинала 2023-07-08 . Получено 2023-07-09 .(3 страницы)
16. Smith, Phillip Hagar (январь 1944 г.). «Улучшенный калькулятор линии передачи — расширение «калькулятора», первоначально опубликованного в журнале ELECTRONICS в январе 1939 г. Добавлены новые параметры и улучшена точность» (PDF) . electronics . Vol. 17, no. 1. New York, USA: McGraw-Hill Publishing Company, Inc. pp. 130–133, 318, 320, 322, 324–325. ISSN  0013-5070. Архивировано (PDF) из оригинала 2023-01-31 . Получено 2023-07-09 .(4+5 страниц)
17. Inan, Aziz S. (2005-07-03). Написано в Школе инженерии Портлендского университета, Портленд, Орегон, США. Вспоминая Филлипа Х. Смита в его 100-й день рождения (PDF) . 2005 IEEE Antennas and Propagation Society International Symposium Digest . Vol. 3B. Вашингтон, округ Колумбия, США: IEEE Antennas and Propagation Society . стр. 129–132. doi :10.1109/APS.2005.1552450. eISSN  1947-1491. ISBN 0-7803-8883-6. ISSN  1522-3965. Архивировано (PDF) из оригинала 2023-07-02 . Получено 2023-07-02 .(Примечание. Это исправленная версия первоначально опубликованной статьи.)
18. Linton, Jr., RL (январь 1950 г.). Написано в Antenna Laboratory, University of California, Berkeley, California, USA. "Graph for Smith Chart" (PDF) . electronics . Vol. 23, no. 1. New York, USA: McGraw-Hill Publishing Company, Inc. pp. 123, 158. ISSN  0013-5070. Архивировано (PDF) из оригинала 2023-01-31 . Получено 2023-07-22 .
19. "Измерение импеданса-Смит Диаграмма с примером" (PDF) . General Radio Experimenter . Том XXV, № 6. Кембридж, Массачусетс, США: General Radio Company . Ноябрь 1950 г. С. 5–7. Архивировано (PDF) из оригинала 22.07.2023 . Получено 22.07.2023 .
20. Позар, Дэвид Майкл (2005). Микроволновая техника (3-е изд.). John Wiley & Sons, Inc. стр. 64–71. ISBN 0-471-44878-8.
21. Гонсалес, Гильермо (1997). Анализ и проектирование СВЧ-транзисторных усилителей (2-е изд.). Нью-Джерси, США: Prentice Hall . стр. 93–103. ISBN 0-13-254335-4.
22. Bevelacqua, Peter Joseph (2013-01-11) [2010]. "The Smith Chart". www.antenna-theory.com . Архивировано из оригинала 2023-07-08 . Получено 2023-07-09 .
23. "Согласование антенн с помощью векторного сетевого анализатора". Tek . Tektronix, Inc. 2017-10-06. Архивировано из оригинала 2023-07-08 . Получено 2023-07-09 .
24. Хейт-младший, Уильям Харт [в Викиданных] (1981). Инженерная электромагнетика (4-е изд.). McGraw-Hill, Inc., стр. 428–433. ISBN 0-07-027395-2.(527 страниц)
25. Дэвидсон, Колин Уильям (1989). Линии передачи для связи с программами САПР (2-е изд.). Бейзингсток, Хэмпшир, Великобритания: Macmillan Education Ltd. стр. 80–85. ISBN 0-333-47398-1. ark:/13960/s2dzmfrhg24 . Получено 2023-07-09 .(viii+244 страницы)
26. Muller, Andrei A.; Soto Pacheco, Pablo; Dascălu, Dan [на румынском] ; Neculoiu, Dan; Boria, Vicente E. (2011). «Трехмерная диаграмма Смита на основе сферы Римана для активных и пассивных микроволновых цепей». IEEE Microwave and Wireless Components Letters . 21 (6). IEEE Microwave Theory and Techniques Society : 286–288. doi :10.1109/LMWC.2011.2132697. hdl : 10251/55107 . ISSN  1531-1309. S2CID  38953650.
27. Мюллер, Андрей А.; Асавей, Виктор; Молдовяну, Алин; Санабрия-Кодесал, Эстер; Хадар, Рияз А.; Попеску, Корнел; Даскэлу, Дан [на румынском языке] ; Ионеску, Адриан М. (ноябрь 2020 г.). «Трехмерная диаграмма Смита: от теории к экспериментальной реальности». Журнал IEEE Microwave . 21 (11). Общество теории и техники IEEE Microwave : 22–35. doi : 10.1109/MMM.2020.3014984. ISSN  1527-3342. S2CID  222296721.

Дальнейшее чтение

• Кэмпбелл, Джордж Эшли (апрель 1911 г.). «Цизоидальные колебания» (PDF) . Труды Американского института инженеров-электриков . XXX (1–6). Американский институт инженеров-электриков : 789–824 [рис. 13 на стр. 810]. doi :10.1109/PAIEE.1911.6659711. S2CID  51647814 . Получено 24.06.2023 .(37 страниц) (Примечание. Включает раннее графическое изображение чего-то похожего на диаграмму Смита за десятилетия до того, как Мидзухаси, Вольперт и Смит опубликовали свои работы.)
• Флеминг, Джон Эмброуз (январь 1912 г.) [май 1911 г.]. Распространение электрических токов в телефонных и телеграфных проводниках: курс аспирантских лекций, прочитанных в Лондонском университете (пересмотренное 2-е изд.). Университетский колледж, Лондон, Великобритания: Constable & Company Ltd. ark:/13960/t3bz6211d . Получено 23 июля 2023 г.(xiv+316 страниц)
• Краусс, Герберт Л. (сентябрь 1949 г.). «Схемы линий передачи». Электротехника . Т. 68, № 9. С. 766–774 [767]. doi :10.1109/EE.1949.6444963. eISSN  2376-7804. ISSN  0095-9197.
• Ли, Дональд (2013-01-30). "Smith Chart Tuning, Part I". SOC Business Unit, Advantest Test Cell Innovations, Advantest Corporation . Архивировано из оригинала 2023-07-09 . Получено 2023-07-09 .(29 страниц)
• Гэмблин, Тревор (2015-07-23). ​​"Математическое построение и свойства диаграммы Смита". allaboutcircuits.com . Архивировано из оригинала 2023-07-09 . Получено 2023-07-09 .
• Staples, John (2015). "Impedance Matching and Smith Charts" (PDF) . Школа ускорителей частиц США (USPAS). Архивировано (PDF) из оригинала 2023-07-09 . Получено 2023-07-09 .(27 страниц)

Внешние ссылки

• "Диаграмма Смита в Excel". excelhero.com . Август 2010 г.Некоммерческая интерактивная диаграмма Смита, которая лучше всего выглядит в Excel 2007+.
• «СимСмит». ae6ty.com .Некоммерческое использование, доступно для Windows, Mac и Linux. Множество обучающих видео по диаграмме Смита. Нет ограничений по размеру схемы. Не ограничивается лестничными схемами.
• "Smith v3". fritz.dellsperger.net . Архивировано из оригинала 2015-03-04.Коммерческая и бесплатная диаграмма Смита для Windows
• «QuickSmith». github.com/niyeradori . 2021-11-02.Бесплатный образовательный веб-инструмент по диаграмме Смита доступен на GitHub .
• "Инструмент 3D-диаграммы Смита". 3dsmithchart.com .Обобщенный инструмент для построения 2D и 3D диаграмм Смита для активных и пассивных цепей (бесплатно для академических/образовательных кругов).