
Колыбель Ньютона — это устройство, обычно сделанное из металла, которое демонстрирует принципы сохранения импульса и сохранения энергии в физике с помощью качающихся сфер . Когда одна сфера на конце поднимается и отпускается, она ударяет по неподвижным сферам, сжимая их и тем самым передавая волну давления через неподвижные сферы, что создает силу , которая толкает последнюю сферу вверх. Последняя сфера качается назад и ударяет по неподвижным сферам, повторяя эффект в противоположном направлении. Устройство названо в честь английского ученого 17-го века сэра Исаака Ньютона и было разработано французским ученым Эдмом Мариоттом . Оно также известно как маятник Ньютона , шары Ньютона , рокер Ньютона или исполнительный шаровой кликер (так как устройство издает щелчок каждый раз, когда шары сталкиваются, что они делают неоднократно в устойчивом ритме ). [1] [2]
Когда один из шариков в конце («первый») тянут вбок, прикрепленная нить заставляет его следовать по восходящей дуге. Когда шарик отпускают, он ударяется о второй шарик и почти останавливается. Шарик на противоположной стороне приобретает большую часть скорости первого шарика и качается по дуге, почти такой же высокой, как высота отпускания первого шарика. Это показывает, что последний шарик получает большую часть энергии и импульса первого шарика. Удар производит звуковую волну , которая распространяется через промежуточные шарики. Любой эффективно эластичный материал, такой как сталь, делает это, пока кинетическая энергия временно сохраняется в виде потенциальной энергии при сжатии материала, а не теряется в виде тепла . Это похоже на отскок одной монеты из ряда соприкасающихся монет путем удара по ней другой монетой, и это происходит даже если первая ударенная монета ограничена нажатием на ее центр таким образом, что она не может двигаться. [ требуется ссылка ]
После первоначального удара во всех шарах происходят небольшие движения, но последний шар получает большую часть начальной энергии от удара первого шара. Когда два (или три) шара падают, два (или три) шара на противоположной стороне отскакивают. Некоторые говорят, что такое поведение демонстрирует сохранение импульса и кинетической энергии при упругих столкновениях. Однако, если сталкивающиеся шары ведут себя так, как описано выше, с одинаковой массой , обладающей одинаковой скоростью до и после столкновений, то любая функция массы и скорости сохраняется в таком событии. [3] Таким образом, это объяснение первого уровня является истинным, но не полным описанием движения.

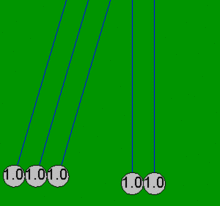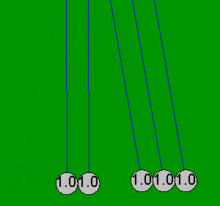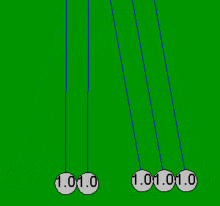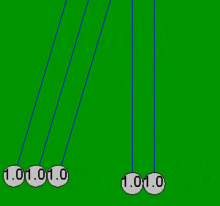
Колыбель Ньютона можно смоделировать довольно точно с помощью простых математических уравнений, предполагая, что шары всегда сталкиваются парами. Если один шар ударяется о четыре неподвижных шара, которые уже соприкасаются, эти простые уравнения не могут объяснить результирующие движения всех пяти шаров, которые не являются следствием потерь на трение . Например, в настоящей колыбели Ньютона четвертый шар совершает некоторое движение, а первый шар совершает небольшое обратное движение. Все анимации в этой статье показывают идеализированное действие (простое решение), которое происходит только в том случае, если шары изначально не соприкасаются и сталкиваются только парами.
Сохранение импульса (масса × скорость) и кинетической энергии ( 1 / 2 × масса × скорость 2 ) можно использовать для нахождения результирующих скоростей для двух сталкивающихся идеально упругих объектов . Эти два уравнения используются для определения результирующих скоростей двух объектов. В случае двух шаров, ограниченных прямой траекторией струнами в колыбели, скорости представляют собой одно число, а не трехмерный вектор для трехмерного пространства, поэтому математика требует только двух уравнений для решения двух неизвестных. Когда два объекта имеют одинаковую массу, решение простое: движущийся объект останавливается относительно неподвижного, а неподвижный подхватывает всю начальную скорость другого. Это предполагает идеально упругие объекты, поэтому нет необходимости учитывать потери тепловой и звуковой энергии.
Сталь не сильно сжимается, но ее эластичность очень эффективна, поэтому она не вызывает большого количества тепла . Простой эффект от двух одинаково массовых эффективно упругих сталкивающихся объектов, ограниченных прямой траекторией, является основой эффекта, наблюдаемого в колыбели, и дает приблизительное решение для всех ее действий.
Для последовательности упругих объектов одинаковой массы, ограниченных прямой траекторией, эффект распространяется на каждый последующий объект. Например, когда два шара падают, чтобы ударить три неподвижных шара в люльке, между двумя упавшими шарами есть незаметное, но критически важное небольшое расстояние, и действие выглядит следующим образом: первый движущийся шар, который ударяет первый неподвижный шар (второй шар, ударяющий третий шар), передает весь свой импульс третьему шару и останавливается. Затем третий шар передает импульс четвертому шару и останавливается, а затем четвертый — пятому шару.
Сразу за этой последовательностью второй движущийся шар передает свой импульс первому движущемуся шару, который только что остановился, и последовательность немедленно и незаметно повторяется за первой последовательностью, выбрасывая четвертый шар прямо за пятым шаром с тем же небольшим расстоянием, которое было между двумя начальными ударяющими шарами. Если они просто соприкасаются, когда ударяют по третьему шару, точность требует более полного решения ниже.
Эффект последнего шара, выбрасываемого со скоростью, почти равной скорости первого шара, можно увидеть, если монета скользит по столу в ряд одинаковых монет, при условии, что ударяющая монета и ее двойные цели находятся на одной прямой. Эффект можно увидеть и в бильярдных шарах. Эффект можно увидеть также, когда резкая и сильная волна давления ударяет по плотному однородному материалу, погруженному в менее плотную среду . Если идентичные атомы , молекулы или более крупные подобъемы плотного однородного материала хотя бы частично упруго связаны друг с другом электростатическими силами, они могут действовать как последовательность сталкивающихся одинаковых упругих шаров.
Окружающие атомы, молекулы или субобъемы, испытывающие волну давления, действуют, чтобы ограничить друг друга подобно тому, как струна ограничивает шары колыбели прямой линией. В качестве медицинского примера, ударные волны литотрипсии могут быть посланы через кожу и ткани без вреда для разрыва камней в почках . Сторона камней, противоположная входящей волне давления, разрывается, а не сторона, принимающая первоначальный удар. В индийской игре карром ударник останавливается после удара по стационарной игровой фигуре, передавая весь свой импульс в фигуру, по которой был нанесен удар.
Для простого решения, точно предсказывающего действие, ни одна пара в процессе столкновения не должна касаться третьего шара, поскольку присутствие третьего шара фактически делает ударенный шар более массивным. Применение двух уравнений сохранения для решения конечных скоростей трех или более шаров в одном столкновении приводит к множеству возможных решений, поэтому этих двух принципов недостаточно для определения результирующего действия.
Даже при небольшом начальном разделении третий шар может быть вовлечен в столкновение, если начальное разделение недостаточно велико. Когда это происходит, необходимо использовать метод полного решения, описанный ниже.
Маленькие стальные шарики работают хорошо, потому что они остаются эффективно эластичными с небольшой потерей тепла при сильных ударах и не сжимаются сильно (примерно до 30 мкм в небольшой колыбели Ньютона). Небольшие, жесткие сжатия означают, что они происходят быстро, менее чем за 200 микросекунд, поэтому стальные шарики с большей вероятностью завершат столкновение до того, как коснутся ближайшего третьего шарика. Более мягкие эластичные шарики требуют большего расстояния, чтобы максимизировать эффект от парных столкновений.
Колыбель, которая лучше всего следует простому решению, должна иметь начальное разделение между шарами, которое измеряет по крайней мере вдвое больше, чем величина, которую сжимает любой шар, но большинство этого не делает. В этом разделе описывается действие, когда начальное разделение недостаточно, и при последующих столкновениях, в которых участвует более двух шаров, даже если есть начальное разделение. Это решение упрощается до простого решения, когда во время столкновения соприкасаются только два шара. Оно применимо ко всем идеально упругим идентичным шарам, которые не теряют энергию из-за трения и могут быть аппроксимированы такими материалами, как сталь, стекло, пластик и резина.
Для двух сталкивающихся шаров для решения двух неизвестных результирующих скоростей нужны только два уравнения сохранения импульса и энергии. Для трех или более одновременно сталкивающихся упругих шаров относительные сжимаемости сталкивающихся поверхностей являются дополнительными переменными, которые определяют результат. Например, пять шаров имеют четыре точки столкновения, и масштабирование (деление) трех из них на четвертую дает три дополнительные переменные, необходимые для решения для всех пяти скоростей после столкновения.
Ньютоновское, лагранжево, гамильтоново и стационарное действие — это различные способы математического выражения классической механики . Они описывают одну и ту же физику, но должны решаться разными методами. Все они обеспечивают сохранение энергии и импульса. Закон Ньютона использовался в исследовательских работах. Он применяется к каждому шару, и сумма сил делается равной нулю. Таким образом, есть пять уравнений, по одному для каждого шара, и пять неизвестных, по одному для каждой скорости. Если шары идентичны, абсолютная сжимаемость поверхностей становится несущественной, потому что ее можно разделить на обе стороны всех пяти уравнений, получив ноль.
Определение скоростей [4] [5] [6] для случая, когда один шар ударяет четыре изначально соприкасающихся шара, осуществляется путем моделирования шаров как грузов с нетрадиционными пружинами на их соударяющихся поверхностях. Большинство материалов, таких как сталь, которые являются эффективно упругими, приблизительно следуют закону силы Гука для пружин, , но поскольку площадь контакта для сферы увеличивается с увеличением силы, соударяющиеся упругие шары следуют корректировке Герца к закону Гука, . Этот закон и закон Ньютона для движения ( ) применяются к каждому шару, давая пять простых, но взаимозависимых дифференциальных уравнений , которые можно решить численно.
Когда пятый шар начинает ускоряться , он получает импульс и энергию от третьего и четвертого шаров через пружинное действие их сжатых поверхностей. Для идентичных упругих шаров любого типа с изначально касающимися шарами действие одинаково для первого удара, за исключением того, что время для завершения столкновения увеличивается в более мягких материалах. Сорок-пятьдесят процентов кинетической энергии начального шара от удара одного шара сохраняется в поверхностях шаров в качестве потенциальной энергии для большей части процесса столкновения. Из начальной скорости 13% передается четвертому шару (что можно рассматривать как движение на 3,3 градуса, если пятый шар движется на 25 градусов), и есть небольшая обратная скорость в первых трех шарах, первый шар имеет наибольшую скорость в −7% от начальной скорости. Это разделяет шары, но они снова сходятся как раз перед тем, как пятый шар возвращается. Это происходит из-за явления маятника, когда различные возмущения под малым углом имеют примерно одинаковое время для возвращения в центр.
Дифференциальные уравнения Герца предсказывают, что если два шара ударят три, пятый и четвертый шары улетят со скоростями в 1,14 и 0,80 раз больше начальной скорости. [7] Это в 2,03 раза больше кинетической энергии пятого шара, чем четвертого шара, что означает, что пятый шар будет качаться в два раза выше в вертикальном направлении, чем четвертый шар. Но в реальной колыбели Ньютона четвертый шар качается на такое же расстояние, как пятый шар. Чтобы объяснить разницу между теорией и экспериментом, два ударяющихся шара должны иметь разделение не менее ≈ 10 мкм (учитывая сталь, 100 г и 1 м/с). Это показывает, что в общем случае стальных шаров незамеченные разделения могут быть важны и должны быть включены в дифференциальные уравнения Герца, или простое решение дает более точный результат.
Предполагалось, что силы в решении Герца выше распространяются в шарах немедленно, что не соответствует действительности. Внезапные изменения силы между атомами материала накапливаются, образуя волну давления. Волны давления (звук) в стали проходят около 5 см за 10 микросекунд, что примерно в 10 раз быстрее, чем время между ударом первого шара и выбрасыванием последнего шара. Волны давления отражаются вперед и назад через все пять шаров примерно десять раз, хотя и рассеиваются до меньшего волнового фронта с большим количеством отражений. Это достаточно быстро для решения Герца, чтобы не требовать существенной модификации для корректировки задержки распространения силы через шары. В менее жестких, но все еще очень эластичных шарах, таких как резина, скорость распространения медленнее, но продолжительность столкновений больше, поэтому решение Герца все еще применимо. Ошибка, вызванная ограниченной скоростью распространения силы, смещает решение Герца в сторону простого решения, поскольку столкновения не так сильно зависят от инерции шаров, находящихся дальше.
Шары одинаковой формы помогают волнам давления сходиться в точке контакта последнего шара: в начальной точке удара одна волна давления идет вперед к другим шарам, а другая идет назад, чтобы отразиться от противоположной стороны первого шара, а затем она следует за первой волной, отставая ровно на один диаметр шара. Две волны встречаются в последней точке контакта, потому что первая волна отражается от противоположной стороны последнего шара и встречается в последней точке контакта со второй волной. Затем они отражаются вперед и назад примерно 10 раз, пока первый шар не перестает соединяться со вторым шаром. Затем реверберации отражаются от точки контакта между вторым и третьим шарами, но все еще сходятся в последней точке контакта, пока последний шар не будет выброшен, но это меньше волнового фронта с каждым отражением.
Использование различных типов материала не меняет действие, пока материал эффективно эластичен. Размер сфер не меняет результаты, если только увеличенный вес не превышает предел упругости материала. Если твердые шары слишком велики, энергия теряется в виде тепла, поскольку предел упругости увеличивается с радиусом, возведенным в степень 1,5, но энергия, которая должна была быть поглощена и выделена, увеличивается как куб радиуса. Сделав контактные поверхности более плоскими, можно преодолеть это в некоторой степени, распределив сжатие на большее количество материала, но это может привести к проблеме выравнивания. Сталь лучше большинства материалов, поскольку она позволяет применять простое решение чаще при столкновениях после первого удара, ее диапазон упругости для хранения энергии остается хорошим, несмотря на более высокую энергию, вызванную ее весом, а больший вес уменьшает эффект сопротивления воздуха.
Наиболее распространенное применение — настольная игрушка для руководителя . Другое применение — образовательная демонстрация физики, как пример сохранения импульса и сохранения энергии .

Принцип, демонстрируемый устройством, закон соударения тел, был впервые продемонстрирован французским физиком аббатом Мариоттом в 17 веке. [1] [8] Его работа по этой теме была впервые представлена Французской академии наук в 1671 году; она была опубликована в 1673 году как Traité de la percussion ou choc des corps («Трактат о сотрясении или ударе тел»). [9]
В своих «Началах» Ньютон признал работу Мариотта, а также Рена, Уоллиса и Гюйгенса пионерами экспериментов по соударениям маятниковых шариков .
Христиан Гюйгенс использовал маятники для изучения столкновений. Его работа De Motu Corporum ex Percussione (О движении тел путем соударения), опубликованная посмертно в 1703 году, содержит версию первого закона Ньютона и рассматривает столкновение подвешенных тел, включающее два тела одинаковой массы, при этом движение движущегося тела передается покоящемуся телу.
Существует много путаницы относительно происхождения современной люльки Ньютона. Мариус Дж. Морин считается первым, кто дал название и создал эту популярную игрушку для руководителей . [ требуется ссылка ] Однако в начале 1967 года английский актер Саймон Преббл придумал название «люлька Ньютона» (теперь оно используется как общее) для деревянной версии, производимой его компанией Scientific Demonstrations Ltd. [10] После некоторого первоначального сопротивления со стороны розничных торговцев они впервые были проданы Harrods of London, тем самым создав начало устойчивого рынка игрушек для руководителей. [ требуется ссылка ] Позже очень успешный хромированный дизайн для магазина Gear на Карнаби-стрит был создан скульптором и будущим кинорежиссером Ричардом Лонкрейном . [ требуется ссылка ]
Самое большое в мире устройство-люлька было спроектировано MythBusters и состояло из пяти однотонных бетонных и стальных арматурных буев, подвешенных к стальной ферме. [ требуется ссылка ] Буи также имели стальную пластину, вставленную между их двумя половинами, чтобы действовать как «точка контакта» для передачи энергии; это устройство-люлька не работало должным образом, потому что бетон неэластичен, поэтому большая часть энергии терялась из-за накопления тепла в бетоне. Меньшая версия, сконструированная ими, состоит из пяти 15-сантиметровых (6 дюймов) шарикоподшипников из хромированной стали, каждый весом 15 килограммов (33 фунта), и почти так же эффективна, как настольная модель.
Устройство-колыбель с самыми большими по диаметру шарами для столкновения, выставленными на всеобщее обозрение, можно было увидеть более года в Милуоки , штат Висконсин, в розничном магазине American Science and Surplus (см. фото). Каждый шар представлял собой надувной мяч для упражнений диаметром 66 см (26 дюймов) (заключенный в стальные кольца) и поддерживался потолком с помощью чрезвычайно сильных магнитов. Он был демонтирован в начале августа 2010 года из-за проблем с техническим обслуживанием. [ необходима цитата ]
Колыбель Ньютона появляется в некоторых фильмах, часто как троп на столе главного злодея, например, в роли Пола Ньюмана в «Подручном Хадсакера» , Магнето в «Людях Икс » и криптонцев в «Супермене 2» . Она использовалась для представления непреклонной позиции НФЛ по отношению к травмам головы в «Сотрясении мозга». [11] Она также использовалась в качестве расслабляющего развлечения на столе главных умных/тревожных/чувствительных персонажей, таких как роль Генри Уинклера в «Ночной смене» , роль Дастина Хоффмана в «Соломенных псах» и роль Гвинет Пэлтроу в «Железном человеке 2» . Она была более заметно представлена в виде серии глиняных горшков в «Розенкранце и Гильденстерне мертвы» и в виде ряда кресел-пузырей Ээро Аарнио 1968 года с полураздетыми женщинами в них в «Геймере» . [12] В Storks у Хантера, генерального директора Cornerstore, есть колыбель не с шариками, а с маленькими птичками. Колыбель Ньютона — предмет в Animal Crossing от Nintendo , где она упоминается как «игрушка для руководителей». [13] В 2017 году эпизод подкаста Omnibus с участием чемпиона Jeopardy! Кена Дженнингса и музыканта Джона Родерика был посвящен истории колыбели Ньютона. [14] Колыбель Ньютона также изображена на столе заместителя директора по коммуникациям Белого дома Сэма Сиборна в The West Wing . В эпизоде Futurama « The Day the Earth Stood Stupid » профессор Хьюберт Фарнсворт показан с головой в колыбели Ньютона и говорящим, что он гений, когда Филип Дж. Фрай проходит мимо.
Прогрессивная рок-группа Dream Theater использует колыбель в качестве образа в обложке своего альбома Octavarium 2005 года . Рок-группа Jefferson Airplane использовала колыбель в альбоме 1968 года Crown of Creation в качестве ритмического устройства для создания полиритмий в инструментальном треке. [ необходима цитата ]