Куб

Твердый объект с шестью равными квадратными гранями.

3D модель куба

В геометрии куб ^[а] — это трехмерный твердый объект , ограниченный шестью квадратными гранями, гранями или сторонами, по три из которых встречаются в каждой вершине . Если смотреть под углом, это шестиугольник , а его сетка обычно изображается в виде креста . ^[1]

Куб — единственный правильный шестигранник и одно из пяти Платоновых тел . У него 6 граней, 12 ребер и 8 вершин.

Куб также является квадратным параллелепипедом , равносторонним кубоидом , прямым ромбоэдром и 3 - зоноэдром . Это правильная квадратная призма в трёх ориентациях и трёхугольный трапецоэдр в четырёх ориентациях.

Куб двойственен октаэдру . _ Он имеет кубическую или октаэдрическую симметрию и является единственным выпуклым многогранником , все грани которого представляют собой квадраты . Его обобщение для пространств более высокой размерности называется гиперкубом .

Ортогональные проекции

Куб имеет четыре специальные ортогональные проекции , центрированные по вершине, ребрам, грани и нормали к фигуре вершины . Первая и третья соответствуют плоскостям Кокстера _А2 и _В2 .

Сферическая черепица

Куб также можно представить в виде сферической мозаики и спроецировать на плоскость посредством стереографической проекции . Эта проекция является равноугольной , сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружностей.

Декартовы координаты

Для куба с центром в начале координат, краями, параллельными осям, и длиной ребра, равной 2, декартовы координаты вершин равны

(±1, ±1, ±1)

а внутренняя часть состоит из всех точек ( x ₀ , x ₁ , x ₂ ) с −1 < x _i < 1 для всех i .

В качестве конфигурации

Эта матрица конфигурации представляет куб. Строки и столбцы соответствуют вершинам, ребрам и граням. Диагональные числа показывают, сколько элементов каждого элемента встречается во всем кубе. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. ^[2] Например, цифра 2 в первом столбце средней строки означает, что на каждом ребре (т. е. на крайних точках) имеется по 2 вершины; цифра 3 в среднем столбце первой строки означает, что в каждой вершине сходятся 3 ребра.

${\displaystyle {\begin{bmatrix}{\begin{matrix}8&3&3\\2&12&2\\4&4&6\end{matrix}}\end{bmatrix}}}$

Уравнение в трехмерном пространстве

В аналитической геометрии поверхность куба с центром ( x ₀ , y ₀ , z ₀ ) и длиной ребра 2a является местом всех точек ( x , y , z ) таких, что

${\displaystyle \max\{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|\}=a.}$

Куб также можно рассматривать как предельный случай трехмерного суперэллипсоида , поскольку все три показателя стремятся к бесконечности.

Формулы

Для куба с длиной ребра : ${\displaystyle a}$

Поскольку объем куба равен третьей степени его сторон , третьи степени называются кубами по аналогии с квадратами и вторыми степенями. ${\displaystyle a\times a\times a}$

Куб имеет наибольший объём среди кубоидов (прямоугольных коробок) с заданной площадью поверхности . Кроме того, куб имеет самый большой объем среди кубоидов с одинаковым общим линейным размером (длина+ширина+высота).

Точка в пространстве

Для куба, описывающая сферу которого имеет радиус R , и для данной точки в его трехмерном пространстве с расстояниями d _i от восьми вершин куба, мы имеем: ^[3]

${\displaystyle {\frac {\sum _{i=1}^{8}d_{i}^{4}}{8}}+{\frac {16R^{4}}{9}}=\left({\frac {\sum _{i=1}^{8}d_{i}^{2}}{8}}+{\frac {2R^{2}}{3}}\right)^{2}.}$

Удвоение куба

Удвоение куба , или Делосская проблема , — это задача, поставленная древнегреческими математиками : они, используя только циркуль и линейку, начали с длины ребра данного куба и построили длину ребра куба с удвоенной длиной ребра. объем исходного куба. Им не удалось решить эту задачу, что в 1837 году Пьер Ванцель доказал невозможностью, поскольку кубический корень из 2 не является конструктивным числом .

Равномерные раскраски и симметрия

Октаэдрическое дерево симметрии

Куб имеет три однородные раскраски, названные по уникальным цветам квадратных граней вокруг каждой вершины: 111, 112, 123.

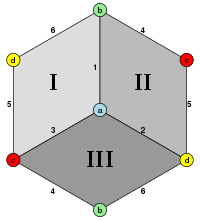
Куб имеет четыре класса симметрии, которые можно представить вершинно-транзитивной раскраской граней. Высшая октаэдрическая симметрия Oh _имеет все грани одного цвета. Двугранная симметрия D _4h возникает из-за того, что куб представляет собой твердое тело, все шесть сторон которого имеют разные цвета. Призматическое подмножество D _2d имеет ту же окраску, что и предыдущее, а D _2h имеет чередующиеся цвета сторон, всего три цвета, спаренные противоположными сторонами. Каждая форма симметрии имеет свой символ Витхоффа .

Геометрические отношения

11 сетей куба

Сетка куба, складывающегося в 3 измерения

Куб имеет одиннадцать сеток : то есть существует одиннадцать способов сплющить полый куб, обрезав семь ребер. ^[4] Чтобы раскрасить куб так, чтобы никакие две соседние грани не имели одинаковый цвет, потребуется как минимум три цвета.

Куб — это ячейка единственного правильного замощения трехмерного евклидова пространства . Оно также уникально среди платоновых тел тем, что имеет грани с четным числом сторон и, следовательно, является единственным членом этой группы, который является зоноэдром ( каждая грань имеет точечную симметрию).

Куб можно разрезать на шесть одинаковых квадратных пирамид . Если эти квадратные пирамиды затем присоединить к граням второго куба, получится ромбдодекаэдр (с парами копланарных треугольников, объединенных в ромбические грани).

В богословии

Кубы появляются в авраамических религиях . Кааба (по - арабски «куб») в Мекке является одним из примеров. Кубики также фигурируют в иудаизме как тфилин , а Новый Иерусалим описывается в Новом Завете как куб. ^[5]

Другие размеры

Аналог куба в четырехмерном евклидовом пространстве имеет особое название — тессеракт или гиперкуб . Точнее, гиперкуб (или n -мерный куб или просто n -куб) является аналогом куба в n -мерном евклидовом пространстве, а тессеракт — это гиперкуб четвертого порядка. Гиперкуб также называют многогранником меры .

Существуют аналоги куба и в более низких измерениях: точка в измерении 0, отрезок в одном измерении и квадрат в двух измерениях.

Связанные многогранники

Двойником куба является октаэдр , показанный здесь с вершинами в центре квадратных граней куба.

Полукуб — ​​это частное куба 2 к 1.

Фактор куба по антиподальному отображению дает проективный многогранник — полукуб .

Если исходный куб имеет длину ребра 1, его двойственный многогранник ( октаэдр ) имеет длину ребра . ${\displaystyle \scriptstyle {\sqrt {2}}/2}$

Куб — частный случай в различных классах общих многогранников:

Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр ; в более общем смысле это называется демикубом . Вместе они образуют правильное соединение — звезду октангулу . Пересечение этих двух форм образует правильный октаэдр. Симметрии правильного тетраэдра соответствуют симметрии куба, который отображает каждый тетраэдр сам в себя; другие симметрии куба отображают их друг на друга.

Один такой правильный тетраэдр имеет объем1/3того же куба. Оставшееся пространство состоит из четырех равных неправильных тетраэдров объемом1/6куба, каждый.

Выпрямленный куб — ​​кубооктаэдр . Если срезать меньшие углы, то получится многогранник с шестью восьмиугольными гранями и восемью треугольными. В частности, мы можем получить правильные восьмиугольники ( усеченный куб ). Ромбокубооктаэдр получается путем срезания на нужную величину как углов, так и ребер .

Куб можно вписать в додекаэдр так, что каждая вершина куба является вершиной додекаэдра, а каждое ребро — диагональю одной из граней додекаэдра; взятие всех таких кубиков дает правильное соединение из пяти кубиков.

Если два противоположных угла куба усечь на глубину трёх непосредственно связанных с ними вершин, то получится неправильный октаэдр. Восемь таких неправильных октаэдров можно прикрепить к треугольным граням правильного октаэдра, чтобы получить кубооктаэдр.

Куб топологически связан с серией сферических многогранников и мозаик с вершинными фигурами третьего порядка .

Кубооктаэдр — один из семейства однородных многогранников, родственных кубу и правильному октаэдру.

Куб топологически связан как часть последовательности правильных мозаик, простирающихся в гиперболическую плоскость : {4,p}, p=3,4,5...

При двугранной симметрии Dih ₄ куб топологически связан в ряд однородных многогранников и мозаик 4.2n.2n, простирающихся в гиперболическую плоскость:

Все эти фигуры обладают октаэдрической симметрией .

Куб является частью последовательности ромбических многогранников и мозаик с симметрией группы Кокстера [ n ,3] . Куб можно рассматривать как ромбический шестигранник, где ромбы — это квадраты.

Куб представляет собой квадратную призму :

Как тригональный трапецоэдр , куб относится к семейству гексагонально-диэдральной симметрии.

В единых сотах и ​​полихоре

Это элемент 9 из 28 выпуклых однородных сот :

Это также элемент пяти четырехмерных однородных полихор :

Кубический граф

Скелет куба (вершины и ребра) образует граф с 8 вершинами и 12 ребрами, называемый графом куба . Это частный случай графа гиперкуба . ^[6] Это один из 5 платоновых графов , каждый из которых представляет собой скелет своего Платонового тела .

Расширением является трехмерный k -ARY граф Хэмминга , который при k = 2 является графом-кубом. Графы такого типа встречаются в теории параллельной обработки на компьютерах.

Смотрите также

• Пирамида
• Тессеракт
• Трапецоэдр
• Куб принца Руперта

Примечания

1. от латинского cubus , от греческого κύβος (kubos)  «куб, игральная кость, позвонок». В свою очередь от протоиндоевропейского *keu(b)- «сгибаться, поворачиваться».

Рекомендации

1. «Сети твердых тел | Геометрия | Сети куба | Сети конуса и цилиндра» .
2. Коксетер 1973, с. 12, §1.8 Конфигурации.
3. Пак, Пу-Сон. «Расстояния регулярных многогранников», Forum Geometricorum 16, 2016, 227–232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf. Архивировано 10 октября 2016 г. в Wayback Machine.
4. Уэхара, Рюхей (2020). «Рисунок 1.1». Введение в вычислительное оригами: мир новой вычислительной геометрии . Сингапур: Спрингер. п. 4. дои : 10.1007/978-981-15-4470-5. ISBN 978-981-15-4469-9. МР  4215620. S2CID  220150682.
5. «Символика Куба • Ева из сада». 30 октября 2020 г.
6. Харари, Фрэнк ; Хейс, Джон П.; Ву, Хорнг-Джых (1988). «Обзор теории графов гиперкубов» (PDF) . Компьютеры и математика с приложениями . 15 (4): 277–289. дои : 10.1016/0898-1221(88)90213-1. hdl : 2027.42/27522 . МР  0949280.

Цитируемые работы

• Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Дувр. стр. 122–123.

Внешние ссылки

• Вайсштейн, Эрик В. «Куб». Математический мир .
• Куб: интерактивная модель многогранника*
• Объем куба с интерактивной анимацией
• Cube (сайт Роберта Уэбба)