Динамика полета самолета

Наука об ориентации и управлении летательными аппаратами в трех измерениях

Динамика полета — это наука об ориентации и управлении воздушным транспортным средством в трех измерениях. Три критических параметра динамики полета — это углы поворота в трех измерениях относительно центра тяжести транспортного средства (цт), известные как тангаж , крен и рыскание . Они вместе известны как положение самолета , часто в основном относительно атмосферной рамки в нормальном полете, но также относительно местности во время взлета или посадки или при работе на малой высоте. Концепция положения не является специфичной для самолетов с фиксированным крылом, но также распространяется на роторные самолеты, такие как вертолеты и дирижабли , где динамика полета, участвующая в установлении и контроле положения, совершенно иная.

Системы управления корректируют ориентацию транспортного средства относительно его ЦТ. Система управления включает в себя поверхности управления, которые при отклонении создают момент (или пару от элеронов) относительно ЦТ, который вращает самолет по тангажу, крену и рысканию. Например, момент тангажа возникает из-за силы, приложенной на расстоянии впереди или сзади ЦТ, заставляя самолет наклоняться вверх или вниз.

Самолет с фиксированным крылом увеличивает или уменьшает подъемную силу, создаваемую крыльями, когда он наклоняет нос вверх или вниз, увеличивая или уменьшая угол атаки (AOA). Угол крена также известен как угол крена на самолете с фиксированным крылом, который обычно «накреняется», чтобы изменить горизонтальное направление полета. Самолет обтекается от носа до хвоста, чтобы уменьшить сопротивление , что делает выгодным поддерживать угол бокового скольжения около нуля, хотя самолет может быть намеренно «согнут вбок», чтобы увеличить сопротивление и скорость снижения во время посадки, чтобы удерживать самолет в том же направлении, что и курс взлетно-посадочной полосы во время посадки при боковом ветре и во время полета с асимметричной тягой. ^[1]

Фон

Roll, pang и yaw относятся к вращениям вокруг соответствующих осей, начиная с определенного состояния равновесия устойчивого полета . Равновесный угол крена известен как уровень крыльев или нулевой угол крена.

Наиболее распространенное авиационное соглашение определяет крен как действующий относительно продольной оси, положительный при правом (правом) крыле вниз. Рыскание относительно вертикальной оси корпуса, положительно при носе к правому борту. Тангаж относительно оси, перпендикулярной продольной плоскости симметрии, положительный при поднятом носе. ^[2]

Системы отсчета

Три правые , декартовы системы координат часто используются в динамике полета. Первая система координат имеет начало, зафиксированное в системе отсчета Земли:

• Земляной каркас
  • Начало координат - произвольное, фиксированное относительно поверхности Земли.
  • x ось _E - положительная в направлении на север
  • y ось _E - положительная в направлении на восток
  • z Ось _E - положительная по направлению к центру Земли

Во многих приложениях динамики полета предполагается, что система отсчета Земли является инерциальной с плоскостью x _E , y _E , хотя систему отсчета Земли можно также рассматривать как сферическую систему координат с началом в центре Земли.

Две другие системы отсчета являются фиксированными относительно тела, с началами, движущимися вместе с самолетом, обычно в центре тяжести. Для самолета, который симметричен справа налево, системы отсчета можно определить следующим образом:

• Каркас кузова
  • Начало - центр тяжести самолета
  • ось x _b - положительная из носа самолета в плоскости симметрии самолета
  • ось z _b - перпендикулярно оси x _b , в плоскости симметрии самолета, положительная снизу самолета
  • ось y _b - перпендикулярна плоскости x _b , z _b , положительная, определяется по правилу правой руки (обычно положительная вне правого крыла)
• Ветровая рама
  • Начало - центр тяжести самолета
  • ось x _w - положительная по направлению вектора скорости самолета относительно воздуха
  • ось z _w - перпендикулярно оси x _w , в плоскости симметрии самолета, положительная снизу самолета
  • ось y _w - перпендикулярна плоскости x _w , z _w , положительная, определяется по правилу правой руки (обычно положительная вправо)

Асимметричные самолеты имеют аналогичные рамы, закрепленные на корпусе, но для выбора точных направлений осей x и z необходимо использовать другие условные обозначения .

Земная система координат является удобной системой координат для выражения поступательной и вращательной кинематики самолета. Земная система координат также полезна тем, что при определенных допущениях ее можно аппроксимировать как инерциальную. Кроме того, одна сила, действующая на самолет, вес, зафиксирована в направлении + z _E.

Рама корпуса часто представляет интерес, поскольку начало и оси остаются фиксированными относительно самолета. Это означает, что относительная ориентация Земли и рам корпуса описывает положение самолета. Кроме того, направление силы тяги обычно фиксировано в раме корпуса, хотя некоторые самолеты могут изменять это направление, например, с помощью вектора тяги .

Ветровая рамка является удобной рамкой для выражения аэродинамических сил и моментов, действующих на самолет. В частности, чистая аэродинамическая сила может быть разделена на компоненты вдоль осей ветровой рамки, с силой сопротивления в направлении − x _w и подъемной силой в направлении − z _w .

Мнемоника для запоминания названий углов

В дополнение к определению систем отсчета, можно определить относительную ориентацию систем отсчета. Относительная ориентация может быть выражена в различных формах, включая:

• Матрицы вращения
• Направляющие косинусы
• Углы Эйлера
• Кватернионы

Различные углы Эйлера, связывающие три системы отсчета, важны для динамики полета. Существует множество соглашений об углах Эйлера, но все последовательности вращения, представленные ниже, используют соглашение zy'-x" . Это соглашение соответствует типу углов Тейта-Брайана , которые обычно называют углами Эйлера. Это соглашение подробно описано ниже для углов Эйлера крена, тангажа и рыскания, которые описывают ориентацию системы отсчета тела относительно системы отсчета Земли. Другие наборы углов Эйлера описаны ниже по аналогии.

Преобразования (Углы Эйлера)

От земного каркаса к каркасу тела

• Сначала поверните оси земной системы координат x _E и y _E вокруг оси z _E на угол рыскания ψ . Это приведет к промежуточной системе отсчета с осями, обозначенными x ' ,y ' ,z ' , где z'=z _E .
• Во-вторых, поверните оси x ' и z ' вокруг оси y ' на угол наклона θ . Это приведет к другой промежуточной системе отсчета с осями, обозначенными x",y",z" , где y"=y ' .
• Наконец, поверните оси y" и z" вокруг оси x" на угол крена φ . Система отсчета, которая получается после трех поворотов, является системой отсчета тела.

На основе приведенных выше условных обозначений поворотов и осей:

• Угол рыскания ψ: угол между севером и проекцией продольной оси самолета на горизонтальную плоскость;
• Угол тангажа θ: угол между продольной осью самолета и горизонталью;
• Угол крена φ: вращение вокруг продольной оси самолета после вращения по рысканию и тангажу.

От земного каркаса к ветровому каркасу

• Угол курса σ: угол между севером и горизонтальной составляющей вектора скорости, который описывает направление движения самолета относительно сторон света.
• Угол траектории полета γ: угол между горизонталью и вектором скорости, который описывает, поднимается ли самолет или снижается.
• Угол крена μ: представляет собой вращение подъемной силы вокруг вектора скорости, которое может указывать на то, поворачивает ли самолет .

При выполнении описанных выше вращений для получения системы отсчета тела из системы отсчета Земли существует следующая аналогия между углами:

• σ, ψ (курс против рыскания)
• γ, θ (траектория полета в зависимости от тангажа)
• μ, φ (Банк против Ролла)

От ветровой рамы к корпусной раме

• угол бокового скольжения β: угол между вектором скорости и проекцией продольной оси самолета на плоскость x _w ,y _w , который описывает, есть ли боковая составляющая скорости самолета

• угол атаки α : угол между плоскостью x _w , y _w и продольной осью самолета и, помимо прочего, является важной переменной при определении величины подъемной силы.

При выполнении вращений, описанных ранее, для получения системы отсчета тела из системы отсчета Земли существует следующая аналогия между углами:

• β, ψ (боковое скольжение против рыскания)
• α , θ (атака против высоты тона)
• (φ = 0) (ничего против броска)

Аналогии

Таким образом, между тремя системами отсчета существуют следующие аналогии:

• Рыскание / Курс / Боковое скольжение (ось Z, вертикальная)
• Тангаж / Траектория полета / Угол атаки (ось Y, крыло)
• Крен / Наклон / ничего (ось X, нос)

Дизайн кейсов

При анализе устойчивости самолета обычно учитывают возмущения относительно номинального устойчивого состояния полета . Поэтому анализ будет применяться, например, предполагая:

Прямой и горизонтальный полет

Поворот с постоянной скоростью

Заход на посадку и посадка

Снимать

Скорость, высота и угол атаки балансировки различны для каждого условия полета, кроме того, самолет будет иметь различную конфигурацию, например, на низкой скорости закрылки могут быть выпущены, а шасси могут быть выпущены.

За исключением асимметричных конструкций (или симметричных конструкций при значительном боковом скольжении), уравнения продольного движения (включая тангаж и подъемную силу) можно рассматривать независимо от бокового движения (включая крен и рыскание).

Далее рассматриваются возмущения относительно номинальной прямой и горизонтальной траектории полета.

Для (относительной) простоты анализа предполагается, что поверхности управления зафиксированы на протяжении всего движения, это устойчивость с фиксированным креплением. Анализ без фиксации требует дальнейшего усложнения, связанного с учетом движения поверхностей управления.

Кроме того, предполагается, что полет происходит в неподвижном воздухе, а самолет рассматривается как твердое тело .

Силы полета

На самолет в полете действуют три силы: вес , тяга и аэродинамическая сила .

Аэродинамическая сила

Составляющие аэродинамической силы

Выражение для расчета аэродинамической силы:

${\displaystyle \mathbf {F} _{A}=\int _{\Sigma }(-\Delta p\mathbf {n} +\mathbf {f} )\,d\sigma }$

где:

${\displaystyle \Delta p\equiv }$Разница между статическим давлением и давлением свободного тока

${\displaystyle \mathbf {n} \equiv }$внешний нормальный вектор элемента площади

${\displaystyle \mathbf {f} \equiv }$вектор касательного напряжения, оказываемого воздухом на тело

${\displaystyle \Sigma \equiv }$адекватная опорная поверхность

в проекции на оси ветра получаем:

${\displaystyle \mathbf {F} _{A}=-(\mathbf {i} _{w}D+\mathbf {j} _{w}Q+\mathbf {k} _{w}L)}$

где:

${\displaystyle D\equiv }$Тащить

${\displaystyle Q\equiv }$Боковая сила

${\displaystyle L\equiv }$Поднимать

Аэродинамические коэффициенты

Динамическое давление свободного тока ${\displaystyle \equiv q={\tfrac {1}{2}}\,\rho \,V^{2}}$

Правильная опорная поверхность ( поверхность крыла , в случае самолетов ) ${\displaystyle \equiv S}$

Коэффициент давления ${\displaystyle \equiv C_{p}={\dfrac {p-p_{\infty }}{q}}}$

Коэффициент трения ${\displaystyle \equiv C_{f}={\dfrac {f}{q}}}$

Коэффициент лобового сопротивления ${\displaystyle \equiv C_{d}={\dfrac {D}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {i_{w}} +C_{f}\mathbf {t} \bullet \mathbf {i_{w}} ]\,d\sigma }$

Коэффициент боковой силы ${\displaystyle \equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma }$

Коэффициент подъемной силы ${\displaystyle \equiv C_{L}={\dfrac {L}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {k_{w}} +C_{f}\mathbf {t} \bullet \mathbf {k_{w}} ]\,d\sigma }$

Необходимо знать C _p и C _f в каждой точке рассматриваемой поверхности.

Безразмерные параметры и аэродинамические режимы

При отсутствии тепловых эффектов существуют три замечательных безразмерных числа:

• Сжимаемость потока:

число Маха ${\displaystyle \equiv M={\dfrac {V}{a}}}$

• Вязкость потока:

Число Рейнольдса ${\displaystyle \equiv Re={\dfrac {\rho Vl}{\mu }}}$

• Разрежение потока:

Число Кнудсена ${\displaystyle \equiv Kn={\dfrac {\lambda }{l}}}$

где:

${\displaystyle a={\sqrt {kR\theta }}\equiv }$скорость звука

${\displaystyle k\equiv }$ удельный коэффициент теплоемкости

${\displaystyle R\equiv }$ газовая постоянная по единице массы

${\displaystyle \theta \equiv }$абсолютная температура

${\displaystyle \lambda ={\dfrac {\mu }{\rho }}{\sqrt {\dfrac {\pi }{2R\theta }}}={\dfrac {M}{Re}}{\sqrt {\dfrac {k\pi }{2}}}\equiv }$ средняя длина свободного пробега

В зависимости от λ возможны три степени разрежения, и соответствующие им движения называются:

• Непрерывный ток (незначительное разрежение): ${\displaystyle {\dfrac {M}{Re}}\ll 1}$
• Переходный ток (умеренное разрежение): ${\displaystyle {\dfrac {M}{Re}}\approx 1}$
• Свободный молекулярный ток (высокое разрежение): ${\displaystyle {\dfrac {M}{Re}}\gg 1}$

Движение тела через поток рассматривается в динамике полета как сплошной поток. Во внешнем слое пространства, окружающего тело, вязкость будет пренебрежимо мала. Однако эффекты вязкости необходимо учитывать при анализе потока вблизи пограничного слоя .

В зависимости от сжимаемости потока можно рассматривать различные виды течений:

• Несжимаемое дозвуковое течение : ${\displaystyle 0<M<0.3}$
• Сжимаемый дозвуковой поток : ${\displaystyle 0.3<M<0.8}$
• Трансзвуковой ток : ${\displaystyle 0.8<M<1.2}$
• Сверхзвуковой поток : ${\displaystyle 1.2<M<5}$
• Гиперзвуковой поток : ${\displaystyle 5<M}$

Уравнение коэффициента сопротивления и аэродинамическая эффективность

Если геометрия тела фиксирована и в случае симметричного полета (β=0 и Q=0), коэффициенты давления и трения являются функциями, зависящими от:

${\displaystyle C_{p}=C_{p}(\alpha ,M,Re,P)}$

${\displaystyle C_{f}=C_{f}(\alpha ,M,Re,P)}$

где:

${\displaystyle \alpha \equiv }$ угол атаки

${\displaystyle P\equiv }$рассматриваемая точка поверхности

При этих условиях коэффициенты лобового сопротивления и подъемной силы являются функциями, зависящими исключительно от угла атаки тела и чисел Маха и Рейнольдса . Аэродинамическая эффективность, определяемая как соотношение между коэффициентами подъемной силы и лобового сопротивления, также будет зависеть от этих параметров.

${\displaystyle {\begin{cases}C_{D}=C_{D}(\alpha ,M,Re)\\C_{L}=C_{L}(\alpha ,M,Re)\\E=E(\alpha ,M,Re)={\dfrac {C_{L}}{C_{D}}}\\\end{cases}}}$

Также можно получить зависимость коэффициента сопротивления относительно коэффициента подъемной силы . Это соотношение известно как уравнение коэффициента сопротивления:

${\displaystyle C_{D}=C_{D}(C_{L},M,Re)\equiv }$уравнение коэффициента сопротивления

Аэродинамическая эффективность имеет максимальное значение E _max относительно C _L там, где касательная линия из начала координат касается графика уравнения коэффициента лобового сопротивления.

Коэффициент сопротивления, C _D , можно разложить двумя способами. Первое типичное разложение разделяет эффекты давления и трения:

${\displaystyle C_{D}=C_{Df}+C_{Dp}{\begin{cases}C_{Df}={\dfrac {D}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }C_{f}\mathbf {t} \bullet \mathbf {i_{w}} \,d\sigma \\C_{Dp}={\dfrac {D}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }(-C_{p})\mathbf {n} \bullet \mathbf {i_{w}} \,d\sigma \end{cases}}}$

Существует второе типичное разложение, учитывающее определение уравнения коэффициента сопротивления. Это разложение разделяет влияние коэффициента подъемной силы в уравнении, получая два члена C _D0 и C _Di. C _D0 известен как паразитный коэффициент сопротивления и является базовым коэффициентом сопротивления при нулевой подъемной силе. C _Di известен как индуцированный коэффициент сопротивления и создается подъемной силой тела.

${\displaystyle C_{D}=C_{D0}+C_{Di}{\begin{cases}C_{D0}=(C_{D})_{C_{L}=0}\\C_{Di}\end{cases}}}$

Параболический и общий коэффициент лобового сопротивления

Хорошей попыткой для коэффициента индуктивного сопротивления является предположение о параболической зависимости подъемной силы.

${\displaystyle C_{Di}=kC_{L}^{2}\Rightarrow C_{D}=C_{D0}+kC_{L}^{2}}$

Аэродинамическая эффективность теперь рассчитывается как:

${\displaystyle E={\dfrac {C_{L}}{C_{D0}+kC_{L}^{2}}}\Rightarrow {\begin{cases}E_{max}={\dfrac {1}{2{\sqrt {kC_{D0}}}}}\\(C_{L})_{Emax}={\sqrt {\dfrac {C_{D0}}{k}}}\\(C_{Di})_{Emax}=C_{D0}\end{cases}}}$

Если конфигурация самолета симметрична относительно плоскости XY, минимальный коэффициент сопротивления равен паразитному сопротивлению самолета.

${\displaystyle C_{Dmin}=(C_{D})_{CL=0}=C_{D0}}$

Однако в случае, если конфигурация асимметрична относительно плоскости XY, минимальное сопротивление отличается от паразитного сопротивления. В этих случаях можно проследить новое приближенное параболическое уравнение сопротивления, оставив минимальное значение сопротивления при нулевом значении подъемной силы.

${\displaystyle C_{Dmin}=C_{DM}\neq (C_{D})_{CL=0}}$

${\displaystyle C_{D}=C_{DM}+k(C_{L}-C_{LM})^{2}}$

Изменение параметров в зависимости от числа Маха

Коэффициент давления изменяется в зависимости от числа Маха по следующей зависимости: ^[4]

${\displaystyle C_{p}={\frac {C_{p0}}{\sqrt {|1-{M_{\infty }}^{2}|}}}}$

где

• C _p — коэффициент сжимаемого давления
• C _p0 — коэффициент несжимаемого давления
• M∞ — число Маха набегающего потока _.

Это соотношение достаточно точно для 0,3 < M < 0,7, а при M = 1 оно становится ∞, что является невозможной физической ситуацией и называется особенностью Прандтля–Глауэрта .

Аэродинамическая сила в определенной атмосфере

см. Аэродинамическая сила

Стабильность

Устойчивость — это способность самолета противодействовать возмущениям траектории полета.

По словам Дэвида П. Дэвиса , существует шесть типов устойчивости самолета: скоростная устойчивость, статическая продольная устойчивость без ручного управления, статическая боковая устойчивость, путевая устойчивость, колебательная устойчивость и спиральная устойчивость. ^{[5] : 164}

Стабильность скорости

Самолет в крейсерском полете обычно имеет стабильную скорость. Если скорость увеличивается, сопротивление увеличивается, что снижает скорость до равновесной для его конфигурации и настройки тяги. Если скорость уменьшается, сопротивление уменьшается, и самолет ускоряется до равновесной скорости, где тяга равна сопротивлению.

Однако при медленном полете из- за сопротивления, вызванного подъемной силой , по мере уменьшения скорости сопротивление увеличивается (и наоборот). Это известно как «задняя часть кривой сопротивления ». Самолет будет нестабилен по скорости, поскольку уменьшение скорости приведет к дальнейшему снижению скорости.

Статическая устойчивость и контроль

Продольная статическая устойчивость

Продольная устойчивость относится к устойчивости самолета по тангажу. Для устойчивого самолета, если самолет наклоняется вверх, крылья и хвост создают момент тангажа вниз, который стремится вернуть самолет в исходное положение. Для неустойчивого самолета нарушение тангажа приведет к увеличению момента тангажа. Продольная статическая устойчивость - это способность самолета восстанавливаться после начального возмущения. Продольная динамическая устойчивость относится к демпфированию этих стабилизирующих моментов, что предотвращает постоянные или увеличивающиеся колебания по тангажу.

Устойчивость направления

Направленная или флюгерная устойчивость связана со статической устойчивостью самолета относительно оси z. Так же, как и в случае продольной устойчивости, желательно, чтобы самолет имел тенденцию возвращаться в состояние равновесия при воздействии некоторой формы возмущения рыскания. Для этого наклон кривой момента рыскания должен быть положительным. Самолет, обладающий этим режимом устойчивости, всегда будет указывать на относительный ветер, отсюда и название флюгерная устойчивость.

Динамическая устойчивость и контроль

Продольные моды

Обычной практикой является вывод характеристического уравнения четвертого порядка для описания продольного движения, а затем его приблизительное факторизация в высокочастотный режим и низкочастотный режим. Принятый здесь подход заключается в использовании качественного знания поведения самолета для упрощения уравнений с самого начала, достигая результата более доступным путем.

Два продольных движения (моды) называются короткопериодными колебаниями тона (КПТО) и фугоидами .

Короткопериодные колебания высоты тона

Короткий ввод (в терминологии систем управления импульс ) по тангажу (обычно через руль высоты в самолете с фиксированным крылом стандартной конфигурации) обычно приводит к перескокам относительно уравновешенного состояния. Переход характеризуется затухающим простым гармоническим движением относительно нового уравновешивания. За время, необходимое для затухания колебаний, траектория меняется очень мало.

Обычно это колебание имеет высокую частоту (следовательно, короткий период) и затухает в течение нескольких секунд. Пример из реальной жизни может включать выбор пилотом нового положения набора высоты, например, 5° носом вверх от исходного положения. Можно использовать короткое, резкое оттягивание назад штурвальной колонки, что обычно приводит к колебаниям относительно нового состояния балансировки. Если колебания плохо затухают, самолету потребуется много времени, чтобы установиться в новом состоянии, что потенциально приводит к колебаниям, вызванным пилотом . Если режим короткого периода нестабилен, пилот, как правило, не сможет безопасно управлять самолетом в течение любого периода времени.

Это затухающее гармоническое движение называется короткопериодным колебанием тангажа; оно возникает из-за тенденции устойчивого самолета указывать в общем направлении полета. По своей природе оно очень похоже на режим флюгера ракетных или ракетных конфигураций. Движение в основном включает в себя положение тангажа (тета) и падение (альфа). Направление вектора скорости относительно инерциальных осей равно . Вектор скорости равен: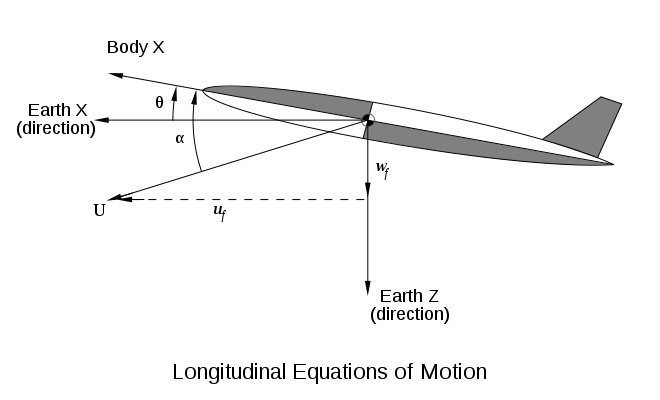 ${\displaystyle \theta }$ ${\displaystyle \alpha }$ ${\displaystyle \theta -\alpha }$

${\displaystyle u_{f}=U\cos(\theta -\alpha )}$

Не удалось проанализировать (SVG (MathML можно включить через плагин для браузера): Недопустимый ответ («Расширение Math не может подключиться к Restbase.») от сервера «http://localhost:6011/en.wikipedia.org/v1/»:): {\displaystyle w_f=U\sin(\theta-\alpha)}

где , - компоненты скорости по осям инерции. Согласно второму закону Ньютона , ускорения пропорциональны силам , поэтому силы по осям инерции равны: ${\displaystyle u_{f}}$ ${\displaystyle w_{f}}$

${\displaystyle X_{f}=m{\frac {du_{f}}{dt}}=m{\frac {dU}{dt}}\cos(\theta -\alpha )-mU{\frac {d(\theta -\alpha )}{dt}}\sin(\theta -\alpha )}$

${\displaystyle Z_{f}=m{\frac {dw_{f}}{dt}}=m{\frac {dU}{dt}}\sin(\theta -\alpha )+mU{\frac {d(\theta -\alpha )}{dt}}\cos(\theta -\alpha )}$

где m — масса . По характеру движения изменение скорости за период колебания пренебрежимо мало, поэтому: ${\displaystyle m{\frac {dU}{dt}}}$

${\displaystyle X_{f}=-mU{\frac {d(\theta -\alpha )}{dt}}\sin(\theta -\alpha )}$

${\displaystyle Z_{f}=mU{\frac {d(\theta -\alpha )}{dt}}\cos(\theta -\alpha )}$

Но силы генерируются распределением давления на теле и относятся к вектору скорости. Но набор осей скорости (ветра) не является инерциальной системой, поэтому мы должны разрешить силы фиксированных осей в оси ветра. Кроме того, нас интересует только сила вдоль оси z:

${\displaystyle Z=-Z_{f}\cos(\theta -\alpha )+X_{f}\sin(\theta -\alpha )}$

Или:

${\displaystyle Z=-mU{\frac {d(\theta -\alpha )}{dt}}}$

Другими словами, сила ветра, действующая на ось, равна центростремительному ускорению.

Уравнение момента представляет собой производную момента импульса по времени :

${\displaystyle M=B{\frac {d^{2}\theta }{dt^{2}}}}$

где M — момент тангажа, а B — момент инерции относительно оси тангажа. Пусть: , скорость тангажа. Уравнения движения со всеми силами и моментами, относящимися к осям ветра, имеют вид: ${\displaystyle {\frac {d\theta }{dt}}=q}$

${\displaystyle {\frac {d\alpha }{dt}}=q+{\frac {Z}{mU}}}$

${\displaystyle {\frac {dq}{dt}}={\frac {M}{B}}}$

Нас интересуют только возмущения сил и моментов, вызванные возмущениями состояний и q, и их производные по времени. Они характеризуются производными устойчивости, определяемыми из условий полета. Возможные производные устойчивости: ${\displaystyle \alpha }$

${\displaystyle Z_{\alpha }}$Подъемная сила, обусловленная падением, отрицательна, поскольку ось z направлена ​​вниз, в то время как положительное направление падения создает восходящую силу.

${\displaystyle Z_{q}}$Подъемная сила, обусловленная скоростью тангажа, возникает из-за увеличения угла атаки хвоста, поэтому она также отрицательна, но мала по сравнению с . ${\displaystyle Z_{\alpha }}$

${\displaystyle M_{\alpha }}$ Момент тангажа из-за падения - термин статической устойчивости. Статическая устойчивость требует, чтобы он был отрицательным.

${\displaystyle M_{q}}$ Момент тангажа, обусловленный скоростью тангажа — параметр демпфирования тангажа, он всегда отрицателен.

Поскольку хвостовое оперение работает в поле обтекания крыла, изменения угла атаки крыла вызывают изменения в нисходящем потоке, но существует задержка, необходимая для того, чтобы изменение поля атаки крыла повлияло на подъемную силу хвостового оперения; это представляется как момент, пропорциональный скорости изменения угла атаки:

${\displaystyle M_{\dot {\alpha }}}$

Эффект замедленного скоса потока воздуха обеспечивает хвосту большую подъемную силу и создает момент, направленный вниз, поэтому ожидается, что он будет отрицательным. ${\displaystyle M_{\dot {\alpha }}}$

Уравнения движения с малыми возмущающими силами и моментами принимают вид:

${\displaystyle {\frac {d\alpha }{dt}}=\left(1+{\frac {Z_{q}}{mU}}\right)q+{\frac {Z_{\alpha }}{mU}}\alpha }$

${\displaystyle {\frac {dq}{dt}}={\frac {M_{q}}{B}}q+{\frac {M_{\alpha }}{B}}\alpha +{\frac {M_{\dot {\alpha }}}{B}}{\dot {\alpha }}}$

Их можно преобразовать, чтобы получить линейное дифференциальное уравнение второго порядка : ${\displaystyle \alpha }$

${\displaystyle {\frac {d^{2}\alpha }{dt^{2}}}-\left({\frac {Z_{\alpha }}{mU}}+{\frac {M_{q}}{B}}+(1+{\frac {Z_{q}}{mU}}){\frac {M_{\dot {\alpha }}}{B}}\right){\frac {d\alpha }{dt}}+\left({\frac {Z_{\alpha }}{mU}}{\frac {M_{q}}{B}}-{\frac {M_{\alpha }}{B}}(1+{\frac {Z_{q}}{mU}})\right)\alpha =0}$

Это представляет собой затухающее простое гармоническое движение.

Мы должны ожидать, что он будет мал по сравнению с единицей, поэтому коэффициент (член «жесткости») будет положительным при условии . Это выражение доминирует над , который определяет продольную статическую устойчивость самолета, он должен быть отрицательным для устойчивости. Член демпфирования уменьшается из-за эффекта скоса потока, и трудно спроектировать самолет как с быстрым естественным откликом, так и с сильным демпфированием. Обычно отклик недостаточно демпфирован, но стабилен. ${\displaystyle {\frac {Z_{q}}{mU}}}$ ${\displaystyle \alpha }$ ${\displaystyle M_{\alpha }<{\frac {Z_{\alpha }}{mU}}M_{q}}$ ${\displaystyle M_{\alpha }}$

Фугоид

Если ручка зафиксирована, самолет не будет поддерживать прямой и горизонтальный полет (за исключением маловероятного случая, когда он будет идеально отрегулирован для горизонтального полета на текущей высоте и тяге), а начнет пикировать, выравниваться и снова набирать высоту. Он будет повторять этот цикл до тех пор, пока не вмешается пилот. Это долгопериодное колебание скорости и высоты называется фугоидным режимом. Это анализируется, предполагая, что SSPO выполняет свою надлежащую функцию и поддерживает угол атаки около номинального значения. Два состояния, которые в основном затрагиваются, — это угол траектории полета (гамма) и скорость. Уравнения движения малых возмущений следующие: ${\displaystyle \gamma }$

${\displaystyle mU{\frac {d\gamma }{dt}}=-Z}$

это означает, что центростремительная сила равна возмущению подъемной силы.

Для скорости, разлагаемой вдоль траектории:

${\displaystyle m{\frac {du}{dt}}=X-mg\gamma }$

где g — ускорение силы тяжести на поверхности Земли . Ускорение вдоль траектории равно чистой силе, действующей по оси x, за вычетом составляющей веса. Мы не должны ожидать, что существенные аэродинамические производные будут зависеть от угла траектории полета, поэтому необходимо учитывать только и . — это приращение сопротивления с увеличением скорости, оно отрицательно, аналогично — это приращение подъемной силы из-за приращения скорости, оно также отрицательно, поскольку подъемная сила действует в противоположном направлении относительно оси z. ${\displaystyle X_{u}}$ ${\displaystyle Z_{u}}$ ${\displaystyle X_{u}}$ ${\displaystyle Z_{u}}$

Уравнения движения принимают вид:

${\displaystyle mU{\frac {d\gamma }{dt}}=-Z_{u}u}$

${\displaystyle m{\frac {du}{dt}}=X_{u}u-mg\gamma }$

Их можно выразить в виде уравнения второго порядка относительно угла траектории полета или возмущения скорости:

${\displaystyle {\frac {d^{2}u}{dt^{2}}}-{\frac {X_{u}}{m}}{\frac {du}{dt}}-{\frac {Z_{u}g}{mU}}u=0}$

Теперь подъемная сила почти равна весу:

${\displaystyle Z={\frac {1}{2}}\rho U^{2}c_{L}S_{w}=W}$

где — плотность воздуха, — площадь крыла, W — вес, а — коэффициент подъемной силы (предполагается постоянным, поскольку угол атаки постоянен), имеем приблизительно: ${\displaystyle \rho }$ ${\displaystyle S_{w}}$ ${\displaystyle c_{L}}$

${\displaystyle Z_{u}={\frac {2W}{U}}={\frac {2mg}{U}}}$

Период фугоиды, T, получается из коэффициента u:

${\displaystyle {\frac {2\pi }{T}}={\sqrt {\frac {2g^{2}}{U^{2}}}}}$

Или:

${\displaystyle T={\frac {2\pi U}{{\sqrt {2}}g}}}$

Поскольку подъемная сила намного больше сопротивления, фугоида в лучшем случае слегка демпфирована. Помог бы пропеллер с фиксированной скоростью. Сильное демпфирование вращения тангажа или большая инерция вращения увеличивают связь между коротким периодом и фугоидными модами, так что они изменят фугоиду.

Боковые моды

Самолет Ан-225 имел крылья неправильной формы , что делало его менее устойчивым, но более маневренным.

В случае симметричной ракеты или снаряда курсовая устойчивость по рысканию такая же, как и устойчивость по тангажу; она напоминает короткопериодные колебания по тангажу, с эквивалентами плоскости рысканья производным устойчивости по тангажу. По этой причине курсовая устойчивость по тангажу и рысканью в совокупности известна как устойчивость «флюгера» ракеты.

Самолеты не имеют симметрии между тангажем и рысканием, поэтому курсовая устойчивость при рыскании выводится из другого набора производных устойчивости. Плоскость рыскания, эквивалентная короткопериодному колебанию тангажа, которая описывает курсовую устойчивость в плоскости рыскания, называется голландским креном. В отличие от движений в плоскости тангажа, боковые моды включают как крен, так и рыскание.

голландский рулет

Обычно уравнения движения выводятся путем формальной манипуляции, что для инженера равносильно математической ловкости рук. Текущий подход следует анализу плоскости тангажа, формулируя уравнения в терминах понятий, которые достаточно знакомы.

Приложение импульса через педали руля направления должно вызвать голландский крен , представляющий собой колебание по крену и рысканию, при этом крен отстает от рысканья на четверть цикла, так что законцовки крыла следуют по эллиптическим траекториям относительно самолета.

Уравнение поступательного движения в плоскости рыскания, как и в плоскости тангажа, приравнивает центростремительное ускорение к боковой силе.

${\displaystyle {\frac {d\beta }{dt}}={\frac {Y}{mU}}-r}$

где (бета) — угол бокового скольжения , Y — боковая сила, а r — скорость рыскания. ${\displaystyle \beta }$

Уравнения моментов немного сложнее. Условие балансировки — самолет находится под углом атаки по отношению к воздушному потоку. Ось x тела не совпадает с вектором скорости, который является опорным направлением для осей ветра. Другими словами, оси ветра не являются главными осями (масса не распределена симметрично относительно осей рыскания и крена). Рассмотрим движение элемента массы в положении -z, x в направлении оси y, т. е. в плоскость бумаги.

Если скорость качения равна p, то скорость частицы равна:

${\displaystyle v=-pz+xr}$

Состоящая из двух членов, сила, действующая на эту частицу, во-первых, пропорциональна скорости изменения v, во-вторых, она обусловлена ​​изменением направления этого компонента скорости по мере движения тела. Последние члены приводят к перекрестным произведениям малых величин (pq, pr, qr), которые позже отбрасываются. В этом анализе они отбрасываются с самого начала ради ясности. По сути, мы предполагаем, что направление скорости частицы из-за одновременных скоростей крена и рыскания существенно не меняется на протяжении всего движения. С этим упрощающим предположением ускорение частицы становится:

${\displaystyle {\frac {dv}{dt}}=-{\frac {dp}{dt}}z+{\frac {dr}{dt}}x}$

Момент рыскания определяется по формуле:

${\displaystyle \delta mx{\frac {dv}{dt}}=-{\frac {dp}{dt}}xz\delta m+{\frac {dr}{dt}}x^{2}\delta m}$

Возникает дополнительный момент рыскания из-за смещения частицы в направлении y: ${\displaystyle {\frac {dr}{dt}}y^{2}\delta m}$

Момент рыскания находится путем суммирования по всем частицам тела:

${\displaystyle N=-{\frac {dp}{dt}}\int xzdm+{\frac {dr}{dt}}\int x^{2}+y^{2}dm=-E{\frac {dp}{dt}}+C{\frac {dr}{dt}}}$

где N — момент рыскания, E — произведение инерции, а C — момент инерции относительно оси рыскания . Аналогичные рассуждения приводят к уравнению крена:

${\displaystyle L=A{\frac {dp}{dt}}-E{\frac {dr}{dt}}}$

где L — момент качения, а A — момент инерции качения.

Производные поперечной и продольной устойчивости

Состояния — (боковое скольжение), r (скорость рыскания) и p (скорость крена) с моментами N (рыскание) и L (крен) и силой Y (вбок). Существует девять производных устойчивости, относящихся к этому движению, ниже объясняется, как они возникают. Однако лучшее интуитивное понимание достигается путем простой игры с моделью самолета и рассмотрения того, как силы на каждом компоненте зависят от изменений в боковом скольжении и угловой скорости: ${\displaystyle \beta }$

${\displaystyle Y_{\beta }}$Боковая сила, возникающая из-за бокового скольжения (при отсутствии рыскания).

Боковое скольжение создает боковую силу от плавника и фюзеляжа. Кроме того, если крыло имеет двугранный угол, боковое скольжение при положительном угле крена увеличивает падение на правом крыле и уменьшает его на левом, что приводит к чистой силовой составляющей, прямо противоположной направлению бокового скольжения. Стреловидность крыльев назад оказывает такое же влияние на падение, но поскольку крылья не наклонены в вертикальной плоскости, одна только обратная стреловидность не влияет . Однако, анэдральная форма может использоваться с большими углами обратной стреловидности в высокопроизводительных самолетах, чтобы компенсировать эффекты падения крыла от бокового скольжения. Как ни странно, это не меняет знак вклада конфигурации крыла в (по сравнению со случаем двугранной формы). ${\displaystyle Y_{\beta }}$ ${\displaystyle Y_{\beta }}$

${\displaystyle Y_{p}}$Боковая сила, вызванная скоростью крена.

Скорость крена вызывает падение на плавник, что создает соответствующую боковую силу. Кроме того, положительный крен (правое крыло вниз) увеличивает подъемную силу на правом крыле и уменьшает ее на левом. Если крыло двугранное, это приведет к боковой силе, которая на мгновение будет противостоять результирующей тенденции к боковому скольжению. Конфигурации крыла и/или стабилизатора с косым углом наклона могут привести к инвертированию знака боковой силы, если эффект плавника будет подавлен.

${\displaystyle Y_{r}}$Боковая сила, вызванная скоростью рыскания.

Рыскание создает боковые силы, действующие на руль направления, киль и фюзеляж.

${\displaystyle N_{\beta }}$Момент рыскания из-за сил бокового скольжения.

Боковое скольжение при отсутствии воздействия руля направления вызывает падение на фюзеляж и хвостовое оперение , тем самым создавая момент рыскания, которому противодействует только жесткость направления, которая будет иметь тенденцию направлять нос самолета назад к ветру в условиях горизонтального полета. В условиях бокового скольжения при заданном угле крена будет иметь тенденцию направлять нос в направлении бокового скольжения даже без воздействия руля направления, вызывая нисходящий спиральный полет. ${\displaystyle N_{\beta }}$

${\displaystyle N_{p}}$Разворачивающий момент, обусловленный скоростью крена.

Скорость крена создает подъемную силу плавника, вызывая момент рыскания, а также дифференциально изменяет подъемную силу на крыльях, тем самым влияя на вклад индуцированного сопротивления каждого крыла, вызывая (небольшой) вклад момента рыскания. Положительный крен обычно вызывает положительные значения, если хвостовое оперение не является угловым или киль не находится ниже оси крена. Боковые компоненты силы, возникающие из-за разницы подъемной силы двугранного или углового крыла, оказывают небольшое влияние, поскольку ось крыла обычно близко выровнена с центром тяжести. ${\displaystyle N_{p}}$ ${\displaystyle N_{p}}$

${\displaystyle N_{r}}$Момент рыскания, обусловленный скоростью рыскания.

Ввод скорости рыскания при любом угле крена генерирует векторы силы руля, плавника и фюзеляжа, которые доминируют над результирующим моментом рыскания. Рыскание также увеличивает скорость внешнего крыла, замедляя внутреннее крыло, с соответствующими изменениями в сопротивлении, вызывающими (небольшой) противодействующий момент рыскания. противодействует присущей направленной жесткости, которая имеет тенденцию направлять нос самолета назад к ветру и всегда соответствует знаку ввода скорости рыскания. ${\displaystyle N_{r}}$

${\displaystyle L_{\beta }}$Момент качения из-за бокового скольжения.

Положительный угол бокового скольжения создает падение оперения, которое может вызывать положительный или отрицательный момент крена в зависимости от его конфигурации. Для любого ненулевого угла бокового скольжения двугранные крылья вызывают вращающийся момент, который стремится вернуть самолет в горизонтальное положение, как и крылья с обратной стреловидностью. При сильно стреловидных крыльях результирующий вращающийся момент может быть чрезмерным для всех требований устойчивости, и для компенсации эффекта вращающегося момента, вызванного стреловидностью крыла, можно использовать антигранные крылья.

${\displaystyle L_{r}}$Кренящий момент из-за скорости рыскания.

Рыскание увеличивает скорость внешнего крыла, одновременно снижая скорость внутреннего, вызывая вращательный момент на внутренней стороне. Вклад плавника обычно поддерживает этот эффект внутреннего вращения, если только он не компенсируется ксеноморфным стабилизатором выше оси крена (или двугранным ниже оси крена).

${\displaystyle L_{p}}$Момент качения, обусловленный скоростью крена.

Крен создает силы противовращения как на правом, так и на левом крыле, одновременно создавая такие силы на хвостовом оперении. Эти противоположные эффекты вращательного момента должны быть преодолены входом элерона, чтобы поддерживать скорость крена. Если крен остановлен при ненулевом угле крена, восходящий вращательный момент, вызванный последующим боковым скольжением, должен вернуть самолет в горизонтальное положение, если только его, в свою очередь, не превзойдет нисходящий вращательный момент, возникающий из-за скорости рыскания, вызванной боковым скольжением. Продольная устойчивость может быть обеспечена или улучшена путем минимизации последнего эффекта. ${\displaystyle L_{\beta }}$ ${\displaystyle L_{r}}$

Уравнения движения

Поскольку голландский крен является режимом управления, аналогичным короткопериодному колебанию тангажа, любое его влияние на траекторию можно игнорировать. Скорость тела r состоит из скорости изменения угла скольжения и скорости поворота. Принимая последнюю за ноль, предполагая отсутствие влияния на траекторию, для ограниченной цели изучения голландского крена:

${\displaystyle {\frac {d\beta }{dt}}=-r}$

Уравнения рыскания и крена с производными устойчивости принимают вид:

${\displaystyle C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p}$(рыскание)

${\displaystyle A{\frac {dp}{dt}}-E{\frac {dr}{dt}}=L_{\beta }\beta -L_{r}{\frac {d\beta }{dt}}+L_{p}p}$(рулон)

Инерционный момент, обусловленный ускорением крена, считается малым по сравнению с аэродинамическими условиями, поэтому уравнения принимают вид:

${\displaystyle -C{\frac {d^{2}\beta }{dt^{2}}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p}$

${\displaystyle E{\frac {d^{2}\beta }{dt^{2}}}=L_{\beta }\beta -L_{r}{\frac {d\beta }{dt}}+L_{p}p}$

Это становится уравнением второго порядка, определяющим либо скорость крена, либо боковое скольжение:

${\displaystyle \left({\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}\right){\frac {d^{2}\beta }{dt^{2}}}+\left({\frac {L_{p}}{A}}{\frac {N_{r}}{C}}-{\frac {N_{p}}{C}}{\frac {L_{r}}{A}}\right){\frac {d\beta }{dt}}-\left({\frac {L_{p}}{A}}{\frac {N_{\beta }}{C}}-{\frac {L_{\beta }}{A}}{\frac {N_{p}}{C}}\right)\beta =0}$

Уравнение для скорости крена идентично. Но угол крена (фи) определяется как: ${\displaystyle \phi }$

${\displaystyle {\frac {d\phi }{dt}}=p}$

Если p — затухающее простое гармоническое движение, то и , но крен должен быть в квадратуре со скоростью крена, а значит, и с боковым скольжением. Движение состоит из колебаний крена и рыскания, причем крен отстает на 90 градусов от рыскания. Концы крыльев вычерчивают эллиптические траектории. ${\displaystyle \phi }$

Устойчивость требует, чтобы термины « жесткость » и «демпфирование» были положительными. Это:

${\displaystyle {\frac {{\frac {L_{p}}{A}}{\frac {N_{r}}{C}}-{\frac {N_{p}}{C}}{\frac {L_{r}}{A}}}{{\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}}}}$(затухание)

${\displaystyle {\frac {{\frac {L_{\beta }}{A}}{\frac {N_{p}}{C}}-{\frac {L_{p}}{A}}{\frac {N_{\beta }}{C}}}{{\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}}}}$ (жесткость)

Знаменатель определяется производной демпфирования крена, которая всегда отрицательна, поэтому знаменатели этих двух выражений будут положительными. ${\displaystyle L_{p}}$

Рассматривая термин «жесткость»: будет положительным, поскольку всегда отрицателен и по своей конструкции положителен. обычно отрицателен, в то время как положителен. Избыточный двугранный угол может дестабилизировать голландский крен, поэтому конфигурации с сильно стреловидными крыльями требуют ксеэдрального угла, чтобы компенсировать вклад стреловидности крыла в . ${\displaystyle -L_{p}N_{\beta }}$ ${\displaystyle L_{p}}$ ${\displaystyle N_{\beta }}$ ${\displaystyle L_{\beta }}$ ${\displaystyle N_{p}}$ ${\displaystyle L_{\beta }}$

Член демпфирования доминирует над произведением демпфирования крена и производных демпфирования рыскания, они оба отрицательны, поэтому их произведение положительно. Голландский крен, следовательно, должен быть демпфирован.

Движение сопровождается небольшим боковым перемещением центра тяжести, и более «точный» анализ введет члены и т. д. Учитывая точность, с которой можно рассчитать производные устойчивости, это излишняя педантичность, которая служит для затемнения связи между геометрией самолета и управляемостью, что является основной целью данной статьи. ${\displaystyle Y_{\beta }}$

Просадка вала

Отклонение ручки в сторону и возвращение ее в центральное положение приводит к изменению ориентации крена.

Движение крена характеризуется отсутствием естественной устойчивости, нет производных устойчивости, которые генерируют моменты в ответ на инерционный угол крена. Возмущение крена вызывает скорость крена, которая отменяется только вмешательством пилота или автопилота . Это происходит при незначительных изменениях в скорости бокового скольжения или рыскания, поэтому уравнение движения сводится к:

${\displaystyle A{\frac {dp}{dt}}=L_{p}p.}$

${\displaystyle L_{p}}$отрицательна, поэтому скорость крена будет уменьшаться со временем. Скорость крена уменьшается до нуля, но прямого контроля над углом крена нет.

Спиральный режим

Просто удерживая ручку неподвижно, когда стартуешь с крыльями, близкими к уровню, самолет обычно будет иметь тенденцию постепенно отклоняться в сторону от прямой траектории полета. Это (слегка нестабильный) спиральный режим . ^{[ требуется цитата ]}

Траектория спирального режима

При изучении траектории интерес представляет направление вектора скорости, а не тела. Направление вектора скорости, спроецированное на горизонталь, будет называться траекторией и обозначаться ( мю ). Ориентация тела называется направлением и обозначается (пси). Уравнение силы движения включает компонент веса: ^{[ требуется цитата ]} ${\displaystyle \mu }$ ${\displaystyle \psi }$

${\displaystyle {\frac {d\mu }{dt}}={\frac {Y}{mU}}+{\frac {g}{U}}\phi }$

где g — ускорение свободного падения, а U — скорость.

Включая производные стабильности:

${\displaystyle {\frac {d\mu }{dt}}={\frac {Y_{\beta }}{mU}}\beta +{\frac {Y_{r}}{mU}}r+{\frac {Y_{p}}{mU}}p+{\frac {g}{U}}\phi }$

Ожидается, что скорости крена и рыскания будут небольшими, поэтому вклады и будут игнорироваться. ${\displaystyle Y_{r}}$ ${\displaystyle Y_{p}}$

Скорость бокового скольжения и крена изменяются постепенно, поэтому их производные по времени игнорируются. Уравнения рыскания и крена сводятся к:

${\displaystyle N_{\beta }\beta +N_{r}{\frac {d\mu }{dt}}+N_{p}p=0}$ (рыскание)

${\displaystyle L_{\beta }\beta +L_{r}{\frac {d\mu }{dt}}+L_{p}p=0}$(рулон)

Решаем для и p : ${\displaystyle \beta }$

${\displaystyle \beta ={\frac {(L_{r}N_{p}-L_{p}N_{r})}{(L_{p}N_{\beta }-N_{p}L_{\beta })}}{\frac {d\mu }{dt}}}$

${\displaystyle p={\frac {(L_{\beta }N_{r}-L_{r}N_{\beta })}{(L_{p}N_{\beta }-N_{p}L_{\beta })}}{\frac {d\mu }{dt}}}$

Подстановка бокового скольжения и скорости крена в уравнение силы приводит к уравнению первого порядка по углу крена:

${\displaystyle {\frac {d\phi }{dt}}=mg{\frac {(L_{\beta }N_{r}-N_{\beta }L_{r})}{mU(L_{p}N_{\beta }-N_{p}L_{\beta })-Y_{\beta }(L_{r}N_{p}-L_{p}N_{r})}}\phi }$

Это экспоненциальный рост или спад, в зависимости от того, является ли коэффициент положительным или отрицательным. Знаменатель обычно отрицателен, что требует (оба произведения положительны). Это находится в прямом противоречии с голландским требованием к устойчивости к крену, и трудно спроектировать самолет, для которого и голландский режим крена, и спиральный режим изначально устойчивы. ^{[ необходима цитата ]} ${\displaystyle \phi }$ ${\displaystyle L_{\beta }N_{r}>N_{\beta }L_{r}}$

Поскольку спиральный режим имеет большую постоянную времени, пилот может вмешаться, чтобы эффективно стабилизировать его, но самолет с нестабильным Dutch Roll будет трудно пилотировать. Обычно проектируют самолет с устойчивым Dutch Roll Mode, но слегка нестабильным Spiral Mode. ^{[ необходима цитата ]}

Смотрите также

• Сокращения и аббревиатуры в авионике
• Аэронавтика
• Устойчивый полет
• Система управления полетом самолета
• Механики летного состава самолетов
• Самолет направляется
• Банк самолетов
• Посадка при боковом ветре
• Динамическое позиционирование
• Поверхности управления полетом
• Динамика вертолета
• JSBSim (программная модель динамики полета с открытым исходным кодом)
• Продольная статическая устойчивость
• Динамика твердого тела
• Матрица вращения
• Движение корабля
• Производные стабильности
• Статическая маржа
• Эффект флюгера
• Планер Райта 1902 года

Ссылки

Примечания

1. Центр технической информации обороны (1981-11-01). DTIC ADA124610: Теория устойчивости и управления неподвижным крылом и методы летных испытаний. Пересмотр. С. V-5.
2. Flightwise Volume 2 - Устойчивость и управление самолетом, Крис Карпентер 1997, Airlife Publishing Ltd., ISBN 1 85310 870 7 , Рисунок 2.6 
3. "MISB Standard 0601" (PDF) . Motion Imagery Standards Board (MISB). Архивировано из оригинала (PDF) 24 марта 2017 г. . Получено 1 мая 2015 г. .Также в Файл:MISB Standard 0601.pdf .
4. Андерсон, Джон Д. (2005). Введение в полет (5-е изд., междунар. изд.). Бостон [ua]: McGraw-Hill. стр. 274–275. ISBN 9780071238182.
5. Дэвис, Дэвид П. (1971). Управление большими реактивными самолетами: объяснение существенных различий в летных качествах реактивных транспортных самолетов и поршневых транспортных самолетов, а также некоторые другие аспекты управления реактивными транспортными самолетами (3-е изд.). Совет по регистрации воздушных судов. ISBN 0903083019.

Библиография

• NK Sinha и N Ananthkrishnan (2013), Элементарная динамика полета с введением в методы бифуркации и продолжения , CRC Press, Taylor & Francis.
• Бабистер, AW (1980). Динамическая устойчивость и реакция самолета (1-е изд.). Оксфорд: Pergamon Press. ISBN 978-0080247687.

Внешние ссылки

• MIXR - платформа моделирования смешанной реальности
• JSBsim, открытая, независимая от платформы библиотека программного обеспечения для управления и динамики полета на языке C++