Матрица вращения

Матрица, представляющая евклидово вращение

В линейной алгебре матрица вращения — это матрица преобразования , которая используется для выполнения вращения в евклидовом пространстве . Например, используя соглашение, приведенное ниже, матрица

${\displaystyle R={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}$

вращает точки в плоскости xy против часовой стрелки на угол θ относительно начала координат двумерной декартовой системы координат . Чтобы выполнить вращение точки плоскости со стандартными координатами v = ( x , y ) , его следует записать в виде вектор-столбца и умножить на матрицу R :

${\displaystyle R\mathbf {v} ={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}={\begin{bmatrix}x\cos \theta -y\sin \theta \\x\sin \theta +y\cos \theta \end{bmatrix}}.}$

Если x и y — координаты конечной точки вектора, где x — косинус, а y — синус, то приведенные выше уравнения становятся формулами тригонометрического угла суммирования . Действительно, матрицу вращения можно рассматривать как формулы тригонометрического суммирования углов в матричной форме. Один из способов понять это — сказать, что у нас есть вектор, расположенный под углом 30° к оси X , и мы хотим повернуть этот угол еще на 45°. Нам просто нужно вычислить координаты конечной точки вектора под углом 75°.

Примеры в этой статье применимы к активным вращениям векторов против часовой стрелки в правосторонней системе координат ( y против часовой стрелки от x ) путем предварительного умножения ( R слева). Если какой-либо из них изменен (например, вращение осей вместо векторов, пассивное преобразование ), то следует использовать обратную матрицу примера, которая совпадает с ее транспонированием .

Поскольку умножение матриц не влияет на нулевой вектор (координаты начала координат), матрицы вращения описывают вращения вокруг начала координат. Матрицы вращения обеспечивают алгебраическое описание таких вращений и широко используются для вычислений в геометрии , физике и компьютерной графике . В некоторой литературе термин « вращение» обобщается и включает в себя неправильные вращения , характеризующиеся ортогональными матрицами с определителем -1 (вместо +1). Они сочетают правильное вращение с отражениями (которые инвертируют ориентацию ). В других случаях, когда отражения не учитываются, собственно метку можно отбросить. В этой статье соблюдается последнее соглашение.

Матрицы вращения представляют собой квадратные матрицы с действительными элементами. Более конкретно, их можно охарактеризовать как ортогональные матрицы с определителем  1; то есть квадратная матрица R является матрицей вращения тогда и только тогда, когда R ^T = R ⁻¹ и det R = 1 . Набор всех ортогональных матриц размера n с определителем +1 представляет собой представление группы , известной как специальная ортогональная группа SO( n ) , одним из примеров которой является группа вращения SO(3) . Набор всех ортогональных матриц размера n с определителем +1 или -1 является представлением (общей) ортогональной группы O( n ) .

В двух измерениях

Поворот вектора против часовой стрелки на угол θ . Вектор изначально выровнен по оси x .

В двух измерениях стандартная матрица вращения имеет следующий вид:

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}.}$

Это вращает векторы-столбцы посредством следующего матричного умножения :

${\displaystyle {\begin{bmatrix}x'\\y'\\\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}{\begin{bmatrix}x\\y\\\end{bmatrix}}.}$

Таким образом, новые координаты ( x ′, y ′) точки ( x , y ) после вращения равны

${\displaystyle {\begin{aligned}x'&=x\cos \theta -y\sin \theta \,\\y'&=x\sin \theta +y\cos \theta \,\end{aligned}}.}$

Примеры

Например, когда вектор

${\displaystyle \mathbf {\hat {x}} ={\begin{bmatrix}1\\0\\\end{bmatrix}}}$

повернут на угол θ , его новые координаты равны

${\displaystyle {\begin{bmatrix}\cos \theta \\\sin \theta \\\end{bmatrix}},}$

и когда вектор

${\displaystyle \mathbf {\hat {y}} ={\begin{bmatrix}0\\1\\\end{bmatrix}}}$

повернут на угол θ , его новые координаты равны

${\displaystyle {\begin{bmatrix}-\sin \theta \\\cos \theta \\\end{bmatrix}}.}$

Направление

Направление вращения вектора — против часовой стрелки, если θ положительное (например, 90°), и по часовой стрелке, если θ отрицательное (например, −90°) для . Таким образом, матрица вращения по часовой стрелке находится как ${\displaystyle R(\theta )}$

${\displaystyle R(-\theta )={\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{bmatrix}}.}$

Двумерный случай — единственный нетривиальный (то есть не одномерный) случай, когда группа матриц вращения коммутативна, так что не имеет значения, в каком порядке выполняются множественные вращения. Альтернативное соглашение использует вращающиеся оси ^[1] , и приведенные выше матрицы также представляют вращение осей по часовой стрелке на угол θ .

Нестандартная ориентация системы координат

Поворот на угол θ с нестандартными осями.

Если используется стандартная правосторонняя декартова система координат , с осью x вправо и осью y вверх, вращение R ( θ ) происходит против часовой стрелки. Если используется левая декартова система координат, где x направлен вправо, а y направлен вниз, R ( θ ) движется по часовой стрелке. Такие нестандартные ориентации редко используются в математике, но распространены в 2D компьютерной графике , начало которой часто находится в верхнем левом углу, а ось Y — вниз по экрану или странице. ^[2]

Ниже приведены другие альтернативные соглашения, которые могут изменить направление вращения, создаваемое матрицей вращения.

Общие 2D-вращения

Особенно полезны матрицы

${\displaystyle {\begin{bmatrix}0&-1\\[3pt]1&0\\\end{bmatrix}},\quad {\begin{bmatrix}-1&0\\[3pt]0&-1\\\end{bmatrix}},\quad {\begin{bmatrix}0&1\\[3pt]-1&0\\\end{bmatrix}}}$

для вращения на 90°, 180° и 270° против часовой стрелки.

Поворот на 180° (в центре) , за которым следует положительный поворот на 90° (слева), эквивалентен одному отрицательному повороту на 90° (положительный 270°) (справа). Каждый из этих рисунков изображает результат вращения относительно вертикального исходного положения (внизу слева) и включает матричное представление перестановки, примененной при вращении (в центре справа), а также другие связанные диаграммы. Подробности см. в разделе «Обозначение перестановок» в Викиверситете.

Связь со сложной плоскостью

С

${\displaystyle {\begin{bmatrix}0&-1\\1&0\end{bmatrix}}^{2}\ =\ {\begin{bmatrix}-1&0\\0&-1\end{bmatrix}}\ =-I,}$

матрицы формы

${\displaystyle {\begin{bmatrix}x&-y\\y&x\end{bmatrix}}}$

образуют кольцо , изоморфное полю комплексных чисел . При этом изоморфизме матрицы вращения соответствуют кругу единичных комплексных чисел , комплексных чисел модуля 1 . ${\displaystyle \mathbb {C} }$

Если отождествить с через линейный изоморфизм, действие матрицы вышеуказанного вида на векторы соответствует умножению на комплексное число x + iy , а повороты соответствуют умножению на комплексные числа по модулю 1 . ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbb {C} }$ ${\displaystyle (a,b)\mapsto a+ib,}$ ${\displaystyle \mathbb {R} ^{2}}$

Поскольку любую матрицу вращения можно записать

${\displaystyle {\begin{pmatrix}\cos t&-\sin t\\\sin t&\cos t\end{pmatrix}},}$

приведенное выше соответствие связывает такую ​​матрицу с комплексным числом

${\displaystyle \cos t+i\sin t=e^{it}}$

(это последнее равенство и есть формула Эйлера ).

В трех измерениях

Положительный поворот на 90° вокруг оси Y (слева) после поворота вокруг оси Z (в центре) дает поворот на 120° вокруг главной диагонали (справа).
В левом верхнем углу — матрицы вращения, в правом нижнем — соответствующие перестановки куба с началом координат в его центре.

Базовые 3D-вращения

Базовое трехмерное вращение (также называемое элементарным вращением) — это вращение вокруг одной из осей системы координат. Следующие три основные матрицы вращения вращают векторы на угол θ вокруг осей x , y или z в трех измерениях, используя правило правой руки , которое кодифицирует их чередующиеся знаки. Обратите внимание, что правило правой руки работает только при умножении . (Эти же матрицы могут также представлять вращение осей по часовой стрелке. ^{[nb 1]} ) ${\displaystyle R\cdot {\vec {x}}}$

${\displaystyle {\begin{alignedat}{1}R_{x}(\theta )&={\begin{bmatrix}1&0&0\\0&\cos \theta &-\sin \theta \\[3pt]0&\sin \theta &\cos \theta \\[3pt]\end{bmatrix}}\\[6pt]R_{y}(\theta )&={\begin{bmatrix}\cos \theta &0&\sin \theta \\[3pt]0&1&0\\[3pt]-\sin \theta &0&\cos \theta \\\end{bmatrix}}\\[6pt]R_{z}(\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta &0\\[3pt]\sin \theta &\cos \theta &0\\[3pt]0&0&1\\\end{bmatrix}}\end{alignedat}}}$

Для векторов-столбцов каждое из этих основных векторных вращений появляется против часовой стрелки, когда ось, вокруг которой они происходят, направлена ​​к наблюдателю, система координат правая, а угол θ положителен. R _z , например, будет вращать в направлении оси y вектор, совмещенный с осью x , что можно легко проверить, оперируя R _z вектором (1,0,0) :

${\displaystyle R_{z}(90^{\circ }){\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}\cos 90^{\circ }&-\sin 90^{\circ }&0\\\sin 90^{\circ }&\quad \cos 90^{\circ }&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}1\\0\\0\\\end{bmatrix}}={\begin{bmatrix}0\\1\\0\\\end{bmatrix}}}$

Это похоже на вращение, производимое вышеупомянутой двумерной матрицей вращения. Ниже приведены альтернативные соглашения, которые могут явно или фактически инвертировать смысл вращения, создаваемого этими матрицами.

Общие 3D-вращения

Другие матрицы трехмерного вращения можно получить из этих трех с помощью умножения матриц . Например, продукт

${\displaystyle {\begin{aligned}R=R_{z}(\alpha )\,R_{y}(\beta )\,R_{x}(\gamma )&={\overset {\text{yaw}}{\begin{bmatrix}\cos \alpha &-\sin \alpha &0\\\sin \alpha &\cos \alpha &0\\0&0&1\\\end{bmatrix}}}{\overset {\text{pitch}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \\\end{bmatrix}}}{\overset {\text{roll}}{\begin{bmatrix}1&0&0\\0&\cos \gamma &-\sin \gamma \\0&\sin \gamma &\cos \gamma \\\end{bmatrix}}}\\&={\begin{bmatrix}\cos \alpha \cos \beta &\cos \alpha \sin \beta \sin \gamma -\sin \alpha \cos \gamma &\cos \alpha \sin \beta \cos \gamma +\sin \alpha \sin \gamma \\\sin \alpha \cos \beta &\sin \alpha \sin \beta \sin \gamma +\cos \alpha \cos \gamma &\sin \alpha \sin \beta \cos \gamma -\cos \alpha \sin \gamma \\-\sin \beta &\cos \beta \sin \gamma &\cos \beta \cos \gamma \\\end{bmatrix}}\end{aligned}}}$

представляет вращение , углы отклонения, тангажа и крена которого равны α , β и γ соответственно. Более формально, это внутреннее вращение, углы Тейта – Брайана которого равны α , β , γ вокруг осей z , y , x соответственно. Аналогично, продукт

${\displaystyle {\begin{aligned}\\R=R_{z}(\gamma )\,R_{y}(\beta )\,R_{x}(\alpha )&={\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\\\end{bmatrix}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \\\end{bmatrix}}{\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \\\end{bmatrix}}\\&={\begin{bmatrix}\cos \beta \cos \gamma &\sin \alpha \sin \beta \cos \gamma -\cos \alpha \sin \gamma &\cos \alpha \sin \beta \cos \gamma +\sin \alpha \sin \gamma \\\cos \beta \sin \gamma &\sin \alpha \sin \beta \sin \gamma +\cos \alpha \cos \gamma &\cos \alpha \sin \beta \sin \gamma -\sin \alpha \cos \gamma \\-\sin \beta &\sin \alpha \cos \beta &\cos \alpha \cos \beta \\\end{bmatrix}}\end{aligned}}}$

представляет собой внешнее вращение, чьи (неправильные) углы Эйлера равны α , β , γ вокруг осей x , y , z .

Эти матрицы производят желаемый эффект только в том случае, если они используются для предварительного умножения векторов-столбцов и (поскольку в общем случае умножение матриц не является коммутативным ) только в том случае, если они применяются в указанном порядке (более подробную информацию см. в разделе «Неоднозначности»). Порядок операций вращения — справа налево; матрица, соседняя с вектором-столбцом, применяется первой, а затем — слева. ^[3]

Преобразование матрицы вращения в ось-угол

Каждое вращение в трех измерениях определяется своей осью (вектор вдоль этой оси не изменяется при вращении), а его угол — величиной вращения вокруг этой оси ( теорема Эйлера о вращении ).

Существует несколько методов вычисления оси и угла на основе матрицы вращения (см. также представление оси-угла ). Здесь мы опишем только метод, основанный на вычислении собственных векторов и собственных значений матрицы вращения. Также можно использовать след матрицы вращения.

Определение оси

Вращение R вокруг оси u можно разложить, используя 3 эндоморфизма P , ( I − P ) и Q (щелкните, чтобы увеличить).

Учитывая матрицу вращения R 3 × 3 , вектор u, параллельный оси вращения, должен удовлетворять

${\displaystyle R\mathbf {u} =\mathbf {u} ,}$

поскольку вращение u вокруг оси вращения должно привести к u . Уравнение, приведенное выше, можно решить для u , которое уникально с точностью до скалярного множителя, если только R = I.

Далее уравнение можно переписать

${\displaystyle R\mathbf {u} =I\mathbf {u} \implies \left(R-I\right)\mathbf {u} =0,}$

который показывает, что u лежит в нулевом пространстве R − I .

С другой стороны, u — собственный вектор R , соответствующий собственному значению λ = 1 . Каждая матрица вращения должна иметь это собственное значение, причем два других собственных значения являются комплексно-сопряженными друг с другом. Отсюда следует, что общая матрица вращения в трех измерениях имеет с точностью до мультипликативной константы только один действительный собственный вектор.

Один из способов определить ось вращения — показать, что:

${\displaystyle {\begin{aligned}0&=R^{\mathsf {T}}0+0\\&=R^{\mathsf {T}}\left(R-I\right)\mathbf {u} +\left(R-I\right)\mathbf {u} \\&=\left(R^{\mathsf {T}}R-R^{\mathsf {T}}+R-I\right)\mathbf {u} \\&=\left(I-R^{\mathsf {T}}+R-I\right)\mathbf {u} \\&=\left(R-R^{\mathsf {T}}\right)\mathbf {u} \end{aligned}}}$

Поскольку ( R − RT ) — кососимметричная матрица , мы можем выбрать u так, ^что

${\displaystyle [\mathbf {u} ]_{\times }=\left(R-R^{\mathsf {T}}\right).}$

Произведение матрицы и вектора становится векторным произведением вектора на самого себя, гарантируя, что результат равен нулю:

${\displaystyle \left(R-R^{\mathsf {T}}\right)\mathbf {u} =[\mathbf {u} ]_{\times }\mathbf {u} =\mathbf {u} \times \mathbf {u} =0\,}$

Следовательно, если

${\displaystyle R={\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\\\end{bmatrix}},}$

затем

${\displaystyle \mathbf {u} ={\begin{bmatrix}h-f\\c-g\\d-b\\\end{bmatrix}}.}$

Величина u , вычисленная таким образом, равна ‖ u ‖ = 2 sin θ , где θ — угол поворота.

Это не работает , если R симметричен. Выше: если R − R ^T равно нулю, то все последующие шаги недействительны. В этом случае необходимо диагонализировать R и найти собственный вектор, соответствующий собственному значению 1.

Определение угла

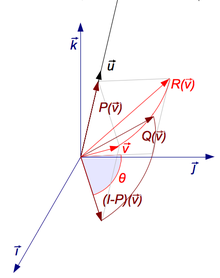
Чтобы найти угол поворота, как только ось вращения известна, выберите вектор v, перпендикулярный оси. Тогда угол поворота — это угол между v и R v .

Однако более прямой метод — просто вычислить след : сумму диагональных элементов матрицы вращения. Следует позаботиться о выборе правильного знака угла θ , соответствующего выбранной оси:

${\displaystyle \operatorname {tr} (R)=1+2\cos \theta ,}$

откуда следует, что абсолютное значение угла равно

${\displaystyle |\theta |=\arccos \left({\frac {\operatorname {tr} (R)-1}{2}}\right).}$

Для оси вращения вы можете получить правильный угол ^[4] из ${\displaystyle \mathbf {n} =(n_{1},n_{2},n_{3})}$

${\displaystyle \left\{{\begin{matrix}\cos \theta &=&{\dfrac {\operatorname {tr} (R)-1}{2}}\\\sin \theta &=&-{\dfrac {\operatorname {tr} (K_{n}R)}{2}}\end{matrix}}\right.}$

где

${\displaystyle K_{n}={\begin{bmatrix}0&-n_{3}&n_{2}\\n_{3}&0&-n_{1}\\-n_{2}&n_{1}&0\\\end{bmatrix}}}$

Матрица вращения по оси и углу

Матрица собственного вращения R на угол θ вокруг оси u = ( u _x , u _y , u _z ) , единичный вектор с u²
_х+ ты²
_года+ ты²
_з= 1 , определяется как: ^[5]

${\displaystyle R={\begin{bmatrix}\cos \theta +u_{x}^{2}\left(1-\cos \theta \right)&u_{x}u_{y}\left(1-\cos \theta \right)-u_{z}\sin \theta &u_{x}u_{z}\left(1-\cos \theta \right)+u_{y}\sin \theta \\u_{y}u_{x}\left(1-\cos \theta \right)+u_{z}\sin \theta &\cos \theta +u_{y}^{2}\left(1-\cos \theta \right)&u_{y}u_{z}\left(1-\cos \theta \right)-u_{x}\sin \theta \\u_{z}u_{x}\left(1-\cos \theta \right)-u_{y}\sin \theta &u_{z}u_{y}\left(1-\cos \theta \right)+u_{x}\sin \theta &\cos \theta +u_{z}^{2}\left(1-\cos \theta \right)\end{bmatrix}}.}$

Вывод этой матрицы из основных принципов можно найти в разделе 9.2 здесь. ^[6] Основная идея получения этой матрицы состоит в разделении проблемы на несколько известных простых шагов.

1. First rotate the given axis and the point such that the axis lies in one of the coordinate planes (xy, yz or zx)
2. Then rotate the given axis and the point such that the axis is aligned with one of the two coordinate axes for that particular coordinate plane (x, y or z)
3. Use one of the fundamental rotation matrices to rotate the point depending on the coordinate axis with which the rotation axis is aligned.
4. Reverse rotate the axis-point pair such that it attains the final configuration as that was in step 2 (Undoing step 2)
5. Reverse rotate the axis-point pair which was done in step 1 (undoing step 1)

This can be written more concisely as

${\displaystyle R=(\cos \theta )\,I+(\sin \theta )\,[\mathbf {u} ]_{\times }+(1-\cos \theta )\,(\mathbf {u} \otimes \mathbf {u} ),}$

where [u]_× is the cross product matrix of u; the expression u ⊗ u is the outer product, and I is the identity matrix. Alternatively, the matrix entries are:

${\displaystyle R_{jk}={\begin{cases}\cos ^{2}{\frac {\theta }{2}}+\sin ^{2}{\frac {\theta }{2}}\left(2u_{j}^{2}-1\right),\quad &{\text{if }}j=k\\2u_{j}u_{k}\sin ^{2}{\frac {\theta }{2}}-\varepsilon _{jkl}u_{l}\sin \theta ,\quad &{\text{if }}j\neq k\end{cases}}}$

where ε_jkl is the Levi-Civita symbol with ε₁₂₃ = 1. This is a matrix form of Rodrigues' rotation formula, (or the equivalent, differently parametrized Euler–Rodrigues formula) with^{[nb 2]}

${\displaystyle \mathbf {u} \otimes \mathbf {u} =\mathbf {u} \mathbf {u} ^{\mathsf {T}}={\begin{bmatrix}u_{x}^{2}&u_{x}u_{y}&u_{x}u_{z}\\[3pt]u_{x}u_{y}&u_{y}^{2}&u_{y}u_{z}\\[3pt]u_{x}u_{z}&u_{y}u_{z}&u_{z}^{2}\end{bmatrix}},\qquad [\mathbf {u} ]_{\times }={\begin{bmatrix}0&-u_{z}&u_{y}\\[3pt]u_{z}&0&-u_{x}\\[3pt]-u_{y}&u_{x}&0\end{bmatrix}}.}$

In ${\displaystyle \mathbb {R} ^{3}}$ the rotation of a vector x around the axis u by an angle θ can be written as:

${\displaystyle R_{\mathbf {u} }(\theta )\mathbf {x} =\mathbf {u} (\mathbf {u} \cdot \mathbf {x} )+\cos \left(\theta \right)(\mathbf {u} \times \mathbf {x} )\times \mathbf {u} +\sin \left(\theta \right)(\mathbf {u} \times \mathbf {x} )}$

or equiviliently:

${\displaystyle R_{\mathbf {u} }(\theta )\mathbf {x} =\mathbf {x} \cos(\theta )+\mathbf {u} (\mathbf {x} \cdot \mathbf {u} )(1-\cos(\theta ))-\mathbf {x} \times \mathbf {u} \sin {\theta }}$

This can also be written in tensor notation as:

${\displaystyle (R_{\mathbf {u} }(\theta )\mathbf {x} )_{i}=(R_{\mathbf {u} }(\theta ))_{ij}{\mathbf {x} }_{j}\quad {\text{with}}\quad (R_{\mathbf {u} }(\theta ))_{ij}=\delta _{ij}\cos(\theta )+\mathbf {u} _{i}\mathbf {u} _{j}(1-\cos(\theta ))-\sin {\theta }\varepsilon _{ijk}\mathbf {u} _{k}}$

If the 3D space is right-handed and θ > 0, this rotation will be counterclockwise when u points towards the observer (Right-hand rule). Explicitly, with ${\displaystyle ({\boldsymbol {\alpha }},{\boldsymbol {\beta }},\mathbf {u} )}$ a right-handed orthonormal basis,

${\displaystyle R_{\mathbf {u} }(\theta ){\boldsymbol {\alpha }}=\cos \left(\theta \right){\boldsymbol {\alpha }}+\sin \left(\theta \right){\boldsymbol {\beta }},\quad R_{\mathbf {u} }(\theta ){\boldsymbol {\beta }}=-\sin \left(\theta \right){\boldsymbol {\alpha }}+\cos \left(\theta \right){\boldsymbol {\beta }},\quad R_{\mathbf {u} }(\theta )\mathbf {u} =\mathbf {u} .}$

Note the striking merely apparent differences to the equivalent Lie-algebraic formulation below.

Properties

For any n-dimensional rotation matrix R acting on ${\displaystyle \mathbb {R} ^{n},}$

${\displaystyle R^{\mathsf {T}}=R^{-1}}$ (The rotation is an orthogonal matrix)

It follows that:

${\displaystyle \det R=\pm 1}$

Вращение называется правильным, если det R = 1 , и неправильным (или рото-отражением), если det R = –1 . Для четных размерностей n = 2 k n собственных значений λ собственного вращения встречаются как пары комплексно-сопряженных чисел , которые являются корнями из единицы: λ = e ^{± iθ _j} для j = 1, ..., k , что действительно только для λ знак равно ±1 . Следовательно, не может быть векторов, фиксируемых вращением ( λ = 1 ), и, следовательно, не может быть оси вращения. Любые фиксированные собственные векторы встречаются парами, а ось вращения представляет собой четномерное подпространство.

Для нечетных размерностей n = 2 k + 1 собственное вращение R будет иметь нечетное количество собственных значений, по крайней мере, с одним λ = 1 , а ось вращения будет нечетномерным подпространством. Доказательство:

${\displaystyle {\begin{aligned}\det \left(R-I\right)&=\det \left(R^{\mathsf {T}}\right)\det \left(R-I\right)=\det \left(R^{\mathsf {T}}R-R^{\mathsf {T}}\right)=\det \left(I-R^{\mathsf {T}}\right)\\&=\det(I-R)=\left(-1\right)^{n}\det \left(R-I\right)=-\det \left(R-I\right).\end{aligned}}}$

Здесь I — единичная матрица, и мы используем det( RT ) = det( R ) = 1 , а также (−1) ⁿ = −1, ^{поскольку} n нечетно . Следовательно, det( R – I ) = 0 , что означает, что существует нулевой вектор v с ( R – I ) v = 0 , то есть R v = v , фиксированный собственный вектор. В четномерном подпространстве, ортогональном v , также могут быть пары фиксированных собственных векторов , поэтому общая размерность фиксированных собственных векторов нечетна.

Например, в 2-пространстве n = 2 вращение на угол θ имеет собственные значения λ = e ^iθ и λ = e ^{- iθ} , поэтому оси вращения нет, за исключением случая θ = 0 , случая нулевого вращения. В трехмерном пространстве n = 3 ось ненулевого собственного вращения всегда является единственной линией, а поворот вокруг этой оси на угол θ имеет собственные значения λ = 1, e ^iθ , e ^{− iθ} . В 4-пространстве n = 4 четыре собственных значения имеют вид e ^{± iθ} , e ^{± iφ} . Нулевое вращение имеет θ = φ = 0 . Случай θ = 0, φ ≠ 0 называется простым вращением , с двумя единичными собственными значениями, образующими плоскость оси , и двумерным вращением, ортогональным плоскости оси. В противном случае осевая плоскость отсутствует. Случай θ = φ называется изоклиническим вращением , в котором собственные значения e ^{± iθ} повторяются дважды, поэтому каждый вектор поворачивается на угол θ .

След матрицы вращения равен сумме ее собственных значений. При n = 2 поворот на угол θ имеет след 2 cos θ . При n = 3 поворот вокруг любой оси на угол θ имеет след 1 + 2 cos θ . Для n = 4 и след равен 2(cos θ + cos φ ) , который становится 4 cos θ для изоклинического вращения.

Примеры

Геометрия

В евклидовой геометрии вращение является примером изометрии , преобразования, которое перемещает точки без изменения расстояний между ними. Вращения отличаются от других изометрий двумя дополнительными свойствами: они оставляют (по крайней мере) одну фиксированную точку и оставляют неизменной « руку ». Напротив, перемещение перемещает каждую точку, отражение меняет местами левый и правый порядок, скользящее отражение делает и то, и другое, а неправильное вращение сочетает в себе изменение левостороннего вращения с нормальным вращением.

Если за начало декартовой системы координат принять фиксированную точку , то каждой точке можно присвоить координаты как смещение от начала координат. Таким образом, можно работать не с самими точками, а с векторным пространством перемещений. Теперь предположим, что ( _p1 , ... _, pn ) — координаты вектора p от начала координат O до точки P. Выберите ортонормированный базис для наших координат; тогда квадрат расстояния до P по Пифагору равен

${\displaystyle d^{2}(O,P)=\|\mathbf {p} \|^{2}=\sum _{r=1}^{n}p_{r}^{2}}$

который можно вычислить с помощью матричного умножения

${\displaystyle \|\mathbf {p} \|^{2}={\begin{bmatrix}p_{1}\cdots p_{n}\end{bmatrix}}{\begin{bmatrix}p_{1}\\\vdots \\p_{n}\end{bmatrix}}=\mathbf {p} ^{\mathsf {T}}\mathbf {p} .}$

Геометрическое вращение преобразует линии в линии и сохраняет соотношения расстояний между точками. Из этих свойств можно показать, что вращение является линейным преобразованием векторов и, следовательно, может быть записано в матричной форме Q p . Тот факт, что вращение сохраняет не только соотношения, но и сами расстояния, формулируется как

${\displaystyle \mathbf {p} ^{\mathsf {T}}\mathbf {p} =(Q\mathbf {p} )^{\mathsf {T}}(Q\mathbf {p} ),}$

или

${\displaystyle {\begin{aligned}\mathbf {p} ^{\mathsf {T}}I\mathbf {p} &{}=\left(\mathbf {p} ^{\mathsf {T}}Q^{\mathsf {T}}\right)(Q\mathbf {p} )\\&{}=\mathbf {p} ^{\mathsf {T}}\left(Q^{\mathsf {T}}Q\right)\mathbf {p} .\end{aligned}}}$

Поскольку это уравнение справедливо для всех векторов p , можно сделать вывод, что каждая матрица вращения Q удовлетворяет условию ортогональности :

${\displaystyle Q^{\mathsf {T}}Q=I.}$

Вращения сохраняют направленность, поскольку они не могут изменить порядок осей, что подразумевает специальное матричное условие:

${\displaystyle \det Q=+1.}$

Не менее важно и то, что можно показать, что любая матрица, удовлетворяющая этим двум условиям, действует как вращение.

Умножение

Обратной матрицей вращения является ее транспонирование, которое также является матрицей вращения:

${\displaystyle {\begin{aligned}\left(Q^{\mathsf {T}}\right)^{\mathsf {T}}\left(Q^{\mathsf {T}}\right)&=QQ^{\mathsf {T}}=I\\\det Q^{\mathsf {T}}&=\det Q=+1.\end{aligned}}}$

Произведение двух матриц вращения представляет собой матрицу вращения:

${\displaystyle {\begin{aligned}\left(Q_{1}Q_{2}\right)^{\mathsf {T}}\left(Q_{1}Q_{2}\right)&=Q_{2}^{\mathsf {T}}\left(Q_{1}^{\mathsf {T}}Q_{1}\right)Q_{2}=I\\\det \left(Q_{1}Q_{2}\right)&=\left(\det Q_{1}\right)\left(\det Q_{2}\right)=+1.\end{aligned}}}$

Для n > 2 умножение матриц вращения n × n обычно не является коммутативным .

${\displaystyle {\begin{aligned}Q_{1}&={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&1\end{bmatrix}}&Q_{2}&={\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}\\Q_{1}Q_{2}&={\begin{bmatrix}0&-1&0\\0&0&1\\-1&0&0\end{bmatrix}}&Q_{2}Q_{1}&={\begin{bmatrix}0&0&1\\1&0&0\\0&1&0\end{bmatrix}}.\end{aligned}}}$

Отмечая, что любая единичная матрица является матрицей вращения и что умножение матриц ассоциативно , мы можем суммировать все эти свойства, сказав, что матрицы вращения размера n × n образуют группу , которая при n > 2 неабелева , называемую специальной ортогональной группой . group и обозначается SO( n ) , SO( n , R ) , SO _n или SO _n ( R ) , группа матриц вращения размера n × n изоморфна группе вращений в n -мерном пространстве. Это означает, что умножение матриц вращения соответствует композиции вращений, применяемых в порядке слева направо к соответствующим матрицам.

Неясности

Ротации псевдонимов и алиби

Интерпретация матрицы вращения может быть неоднозначной.

В большинстве случаев эффект неоднозначности эквивалентен эффекту инверсии матрицы вращения ( для этих ортогональных матриц эквивалентно транспонирование матрицы ).

Трансформация псевдонима или алиби (пассивного или активного)

Координаты точки P могут измениться как из-за поворота системы координат CS ( алиас ), так и из-за поворота точки P ( алиби ). В последнем случае вращение P также приводит к вращению вектора v , представляющего P . Другими словами, либо P и v фиксированы, пока CS вращается (псевдоним), либо CS фиксирован, пока P и v вращаются (алиби). Любое вращение можно законно описать обоими способами, поскольку векторы и системы координат фактически вращаются относительно друг друга вокруг одной оси, но в противоположных направлениях. В этой статье мы выбрали подход алиби для описания вращений. Например,

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}}$

представляет собой поворот вектора v против часовой стрелки на угол θ или поворот CS на тот же угол, но в противоположном направлении (т.е. по часовой стрелке). Преобразования Алиби и псевдонимов также известны как активные и пассивные преобразования соответственно.

Предварительное или пост-умножение

Одна и та же точка P может быть представлена ​​либо вектором -столбцом v , либо вектором-строкой w . Матрицы вращения могут либо предварительно умножать векторы-столбцы ( R v ), либо после умножать векторы-строки ( w R ). Однако R v вызывает вращение в направлении, противоположном w R . В этой статье повороты векторов-столбцов описываются посредством предварительного умножения. Чтобы получить точно такое же вращение ( т.е. те же конечные координаты точки ^P ) , эквивалентный вектор-строка должен быть умножен на транспонирование R (т.е. wRT ) .

Правые или левые координаты

Матрица и вектор могут быть представлены относительно правой или левой системы координат. На протяжении всей статьи мы предполагали правостороннюю ориентацию, если не указано иное.

Векторы или формы

Векторное пространство имеет двойственное пространство линейных форм , и матрица может действовать как на векторы, так и на формы.

Разложения

Независимые самолеты

Рассмотрим матрицу вращения 3 × 3

${\displaystyle Q={\begin{bmatrix}0.36&0.48&-0.80\\-0.80&0.60&0.00\\0.48&0.64&0.60\end{bmatrix}}.}$

Если Q действует в определенном направлении v просто как масштабирование с коэффициентом λ , то мы имеем

${\displaystyle Q\mathbf {v} =\lambda \mathbf {v} ,}$

так что

${\displaystyle \mathbf {0} =(\lambda I-Q)\mathbf {v} .}$

Таким образом, λ является корнем характеристического многочлена для Q ,

${\displaystyle {\begin{aligned}0&{}=\det(\lambda I-Q)\\&{}=\lambda ^{3}-{\tfrac {39}{25}}\lambda ^{2}+{\tfrac {39}{25}}\lambda -1\\&{}=(\lambda -1)\left(\lambda ^{2}-{\tfrac {14}{25}}\lambda +1\right).\end{aligned}}}$

Обращают на себя внимание две особенности. Во-первых, один из корней (или собственных значений ) равен 1, что говорит нам о том, что на какое-то направление матрица не влияет. Для вращений в трех измерениях это ось вращения (понятие, не имеющее смысла ни в каком другом измерении). Во-вторых, два других корня представляют собой пару комплексно-сопряженных чисел, произведение которых равно 1 (постоянный член квадратичного уравнения), а сумма равна 2 cos θ (отрицаемый линейный член). Эта факторизация представляет интерес для матриц вращения 3 × 3 , поскольку со всеми ними происходит одно и то же. (В особых случаях для нулевого поворота «комплексно-сопряженные» оба равны 1, а для поворота на 180 ° они оба равны -1.) Кроме того, аналогичная факторизация справедлива для любой матрицы вращения n × n . Если размерность n нечетна, будет «висящее» собственное значение, равное 1; и для любого измерения остальные полиномиальные факторы разлагаются на квадратичные члены, подобные этому (с учетом двух особых случаев). Нам гарантируется, что характеристический полином будет иметь степень n и, следовательно, n собственных значений. А поскольку матрица вращения коммутирует со своим транспонированием, это нормальная матрица , поэтому ее можно диагонализировать. Мы заключаем, что каждая матрица вращения, выраженная в подходящей системе координат, разбивается на независимые вращения двумерных подпространств, не болеен/2из них.

Сумма элементов главной диагонали матрицы называется следом ; он не меняется, если мы переориентируем систему координат, и всегда равен сумме собственных значений. Для матриц вращения 2 × 2 и 3 × 3 это удобно , поскольку след показывает угол поворота θ в двумерном пространстве (или подпространстве). Для матрицы 2 × 2 след равен 2 cos θ , а для матрицы 3 × 3 — 1 + 2 cos θ . В трехмерном случае подпространство состоит из всех векторов, перпендикулярных оси вращения (инвариантное направление с собственным значением 1). Таким образом, мы можем извлечь из любой матрицы вращения 3 × 3 ось вращения и угол, и они полностью определяют вращение.

Последовательные углы

Ограничения на матрицу вращения 2 × 2 подразумевают, что она должна иметь вид

${\displaystyle Q={\begin{bmatrix}a&-b\\b&a\end{bmatrix}}}$

с a ² + b ² = 1 . Следовательно, мы можем установить a = cos θ и b = sin θ для некоторого угла θ . Чтобы найти θ, недостаточно посмотреть только на a или b ; мы должны рассмотреть оба вместе, чтобы поместить угол в правильный квадрант , используя функцию арктангенса с двумя аргументами .

Теперь рассмотрим первый столбец матрицы вращения 3 × 3 :

${\displaystyle {\begin{bmatrix}a\\b\\c\end{bmatrix}}.}$

Хотя a ² + b ^{2 ,} вероятно, будет равняться не 1, а некоторому значению r ² < 1 , мы можем использовать небольшую вариацию предыдущего вычисления, чтобы найти так называемое вращение Гивенса , которое преобразует столбец в

${\displaystyle {\begin{bmatrix}r\\0\\c\end{bmatrix}},}$

обнуление б . Это действует на подпространство, охватываемое осями x и y . Затем мы можем повторить процесс для xz -подпространства до нуля c . Действуя на полную матрицу, эти два вращения создают схематическую форму.

${\displaystyle Q_{xz}Q_{xy}Q={\begin{bmatrix}1&0&0\\0&\ast &\ast \\0&\ast &\ast \end{bmatrix}}.}$

Переключив внимание на второй столбец, вращение Гивенса подпространства yz теперь может обнулить значение z . Это приводит полную матрицу к виду

${\displaystyle Q_{yz}Q_{xz}Q_{xy}Q={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},}$

что является единичной матрицей. Таким образом, мы разложили Q как

${\displaystyle Q=Q_{xy}^{-1}Q_{xz}^{-1}Q_{yz}^{-1}.}$

Матрица вращения размера n × n будет иметь ( n − 1) + ( n − 2) + ⋯ + 2 + 1 или

${\displaystyle \sum _{k=1}^{n-1}k={\frac {1}{2}}n(n-1)}$

записи ниже диагонали до нуля. Мы можем обнулить их, расширив ту же идею прохождения через колонны серией поворотов в фиксированной последовательности плоскостей. Приходим к выводу, что набор матриц вращения размера n × n , каждая из которых имеет n ² элементов, можно параметризовать формулой1/2n ( n − 1) углов.

В трех измерениях это повторяет в матричной форме наблюдение, сделанное Эйлером , поэтому математики называют упорядоченную последовательность трех углов углами Эйлера . Однако ситуация несколько сложнее, чем мы до сих пор указывали. Несмотря на небольшую размерность, на самом деле у нас есть значительная свобода в используемой нами последовательности пар осей; а еще у нас есть некоторая свобода в выборе ракурсов. Таким образом, мы обнаруживаем множество различных соглашений, используемых при параметризации трехмерного вращения в физике, медицине, химии или других дисциплинах. Когда мы включаем опцию мировых осей или осей тела, возможны 24 различные последовательности. И хотя некоторые дисциплины называют любую последовательность углами Эйлера, другие дают разные названия (Кардано, Тейта-Брайана, крен-тангаж-рыскание ) различным последовательностям.

Одна из причин большого количества вариантов заключается в том, что, как отмечалось ранее, вращения в трех измерениях (и выше) не коммутируют. Если мы поменяем заданную последовательность вращений, мы получим другой результат. Это также означает, что мы не можем составить два вращения, сложив соответствующие им углы. Таким образом, углы Эйлера не являются векторами , несмотря на внешнее сходство в виде тройки чисел.

Вложенные размеры

Матрица вращения 3 × 3 , такая как

${\displaystyle Q_{3\times 3}={\begin{bmatrix}\cos \theta &-\sin \theta &{\color {CadetBlue}0}\\\sin \theta &\cos \theta &{\color {CadetBlue}0}\\{\color {CadetBlue}0}&{\color {CadetBlue}0}&{\color {CadetBlue}1}\end{bmatrix}}}$

предлагает матрицу вращения 2 × 2 ,

${\displaystyle Q_{2\times 2}={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}},}$

встроен в верхний левый угол:

${\displaystyle Q_{3\times 3}=\left[{\begin{matrix}Q_{2\times 2}&\mathbf {0} \\\mathbf {0} ^{\mathsf {T}}&1\end{matrix}}\right].}$

Это не иллюзия; не одна, а множество копий n -мерных вращений находятся внутри ( n + 1) -мерных вращений в виде подгрупп . Каждое вложение оставляет фиксированным одно направление, которое в случае матриц 3 × 3 является осью вращения. Например, у нас есть

${\displaystyle {\begin{aligned}Q_{\mathbf {x} }(\theta )&={\begin{bmatrix}{\color {CadetBlue}1}&{\color {CadetBlue}0}&{\color {CadetBlue}0}\\{\color {CadetBlue}0}&\cos \theta &-\sin \theta \\{\color {CadetBlue}0}&\sin \theta &\cos \theta \end{bmatrix}},\\[8px]Q_{\mathbf {y} }(\theta )&={\begin{bmatrix}\cos \theta &{\color {CadetBlue}0}&\sin \theta \\{\color {CadetBlue}0}&{\color {CadetBlue}1}&{\color {CadetBlue}0}\\-\sin \theta &{\color {CadetBlue}0}&\cos \theta \end{bmatrix}},\\[8px]Q_{\mathbf {z} }(\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta &{\color {CadetBlue}0}\\\sin \theta &\cos \theta &{\color {CadetBlue}0}\\{\color {CadetBlue}0}&{\color {CadetBlue}0}&{\color {CadetBlue}1}\end{bmatrix}},\end{aligned}}}$

фиксация оси x , оси y и оси z соответственно. Ось вращения не обязательно должна быть осью координат; если u = ( x , y , z ) — единичный вектор в нужном направлении, то

${\displaystyle {\begin{aligned}Q_{\mathbf {u} }(\theta )&={\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\sin \theta +\left(I-\mathbf {u} \mathbf {u} ^{\mathsf {T}}\right)\cos \theta +\mathbf {u} \mathbf {u} ^{\mathsf {T}}\\[8px]&={\begin{bmatrix}\left(1-x^{2}\right)c_{\theta }+x^{2}&-zs_{\theta }-xyc_{\theta }+xy&ys_{\theta }-xzc_{\theta }+xz\\zs_{\theta }-xyc_{\theta }+xy&\left(1-y^{2}\right)c_{\theta }+y^{2}&-xs_{\theta }-yzc_{\theta }+yz\\-ys_{\theta }-xzc_{\theta }+xz&xs_{\theta }-yzc_{\theta }+yz&\left(1-z^{2}\right)c_{\theta }+z^{2}\end{bmatrix}}\\[8px]&={\begin{bmatrix}x^{2}(1-c_{\theta })+c_{\theta }&xy(1-c_{\theta })-zs_{\theta }&xz(1-c_{\theta })+ys_{\theta }\\xy(1-c_{\theta })+zs_{\theta }&y^{2}(1-c_{\theta })+c_{\theta }&yz(1-c_{\theta })-xs_{\theta }\\xz(1-c_{\theta })-ys_{\theta }&yz(1-c_{\theta })+xs_{\theta }&z^{2}(1-c_{\theta })+c_{\theta }\end{bmatrix}},\end{aligned}}}$

где c _θ = cos θ , s _θ = sin θ , представляет собой поворот на угол θ , оставляющий ось u неподвижной.

Направление в ( n + 1) -мерном пространстве будет единичным вектором величины, который мы можем рассматривать как точку на обобщенной ^сфере Sn . Таким образом, группу вращений SO( n ⁺ 1) естественно описать как комбинацию SO( n ) и Sn . Подходящим формализмом является расслоение ,

${\displaystyle SO(n)\hookrightarrow SO(n+1)\to S^{n},}$

где для каждого направления в базовом пространстве Sn слой над ним в общем пространстве ^SO ( n + 1) является копией расслоенного пространства SO( n ) , а именно вращений, которые удерживают это направление фиксированным.

Таким образом, мы можем построить матрицу вращения размера n × n , начав с матрицы размера 2 × 2 , направив ее фиксированную ось на S ² (обычную сферу в трехмерном пространстве), направив полученное вращение на S ³ и так далее до конца. S ^{n -1} . Точку на ^Sn можно выбрать с помощью n чисел, поэтому мы снова имеем1/2n ( n - 1) чисел для описания любой матрицы вращения размера n × n .

Фактически, мы можем рассматривать последовательное угловое разложение, обсуждавшееся ранее, как обращение этого процесса вспять. Композиция из n - 1 вращений Гивенса приводит первый столбец (и строку) к (1, 0, ..., 0) , так что оставшаяся часть матрицы представляет собой матрицу вращения размером на единицу меньше, встроенную так, чтобы оставить (1, 0, ..., 0) исправлено.

Параметры асимметрии по формуле Кэли

Когда матрица вращения Q размера n × n не включает в себя собственное значение -1, то есть ни одно из плоских вращений, которые она содержит, не является поворотом на 180°, тогда Q + I является обратимой матрицей . Большинство матриц вращения соответствуют этому описанию, и для них можно показать, что ( Q − I )( Q + I ) ⁻¹ является кососимметричной матрицей , A . Таким образом, А ^Т = − А ; а поскольку диагональ обязательно равна нулю и поскольку верхний треугольник определяет нижний, то A содержит1/2n ( n − 1) независимых чисел.

Удобно, что I − A обратимо, если A кососимметричен; таким образом, мы можем восстановить исходную матрицу, используя преобразование Кэли ,

${\displaystyle A\mapsto (I+A)(I-A)^{-1},}$

который отображает любую кососимметричную матрицу A в матрицу вращения. Фактически, за исключением отмеченных исключений, таким способом мы можем создать любую матрицу вращения. Хотя в практических приложениях мы вряд ли можем позволить себе игнорировать поворот на 180°, преобразование Кэли по-прежнему остается потенциально полезным инструментом, позволяющим параметризовать большинство матриц вращения без тригонометрических функций.

Например, в трех измерениях мы имеем (Кейли, 1846 г.)

${\displaystyle {\begin{aligned}&{\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}\mapsto \\[3pt]\quad {\frac {1}{1+x^{2}+y^{2}+z^{2}}}&{\begin{bmatrix}1+x^{2}-y^{2}-z^{2}&2xy-2z&2y+2xz\\2xy+2z&1-x^{2}+y^{2}-z^{2}&2yz-2x\\2xz-2y&2x+2yz&1-x^{2}-y^{2}+z^{2}\end{bmatrix}}.\end{aligned}}}$

Если мы объединим асимметричные записи в вектор ( x , y , z ) , то мы создадим поворот на 90° вокруг оси x для (1, 0, 0), вокруг оси y для (0, 1, 0), 0) и вокруг оси z для (0, 0, 1). Поворот на 180° просто недосягаем; ибо в пределе x → ∞ ( x , 0, 0) приближается к повороту на 180 ° вокруг оси x , и аналогично для других направлений.

Разложение на ножницы

В двумерном случае матрицу вращения можно разложить на три матрицы сдвига (Paeth 1986):

${\displaystyle {\begin{aligned}R(\theta )&{}={\begin{bmatrix}1&-\tan {\frac {\theta }{2}}\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\\sin \theta &1\end{bmatrix}}{\begin{bmatrix}1&-\tan {\frac {\theta }{2}}\\0&1\end{bmatrix}}\end{aligned}}}$

Это полезно, например, в компьютерной графике, поскольку сдвиг можно реализовать с помощью меньшего количества инструкций умножения, чем непосредственное вращение растрового изображения. На современных компьютерах это может не иметь значения, но может быть актуально для очень старых или младших микропроцессоров.

Вращение также можно записать как два среза и масштабирование (Daubechies & Sweldens 1998):

${\displaystyle {\begin{aligned}R(\theta )&{}={\begin{bmatrix}1&0\\\tan \theta &1\end{bmatrix}}{\begin{bmatrix}1&-\sin \theta \cos \theta \\0&1\end{bmatrix}}{\begin{bmatrix}\cos \theta &0\\0&{\frac {1}{\cos \theta }}\end{bmatrix}}\end{aligned}}}$

Теория групп

Ниже приведены некоторые основные факты о роли совокупности всех матриц вращения фиксированной размерности (здесь в основном 3) в математике и особенно в физике, где вращательная симметрия является требованием каждого действительно фундаментального закона (из-за предположения об изотропии пространства). ), и где та же самая симметрия, если она присутствует, является упрощающим свойством многих проблем менее фундаментального характера. Примеры изобилуют классической механикой и квантовой механикой . Знание части решений, относящихся к этой симметрии, применимо (с оговорками) ко всем таким проблемам, и его можно исключить из конкретной конкретной проблемы, тем самым уменьшив ее сложность. Ярким примером – в математике и физике – может быть теория сферических гармоник . Их роль в групповой теории групп вращений состоит в том, что они являются пространством представления всего множества конечномерных неприводимых представлений группы вращений SO (3). По этой теме см. Группа вращения SO (3) § Сферические гармоники .

К основным статьям, перечисленным в каждом подразделе, приводятся более подробные ссылки.

Группа лжи

Матрицы вращения размера n × n для каждого n образуют группу , специальную ортогональную группу SO( n ) . Эта алгебраическая структура связана с топологической структурой, унаследованной от нее таким образом, что операции умножения и обратного являются аналитическими функциями элементов матрицы. Таким образом, SO( n ) для каждого n является группой Ли . Он компактен и связан , но не просто связан . Это также полупростая группа , фактически простая группа за исключением SO(4). ^[7] Актуальность этого состоит в том, что все теоремы и весь механизм теории аналитических многообразий (аналитические многообразия, в частности, являются гладкими многообразиями ) применимы, и хорошо развитая теория представлений компактных полупростых групп готова к использованию. ${\displaystyle \operatorname {GL} _{n}(\mathbb {R} )}$

Алгебра Ли

Алгебра Ли so ( n ) группы SO( n ) задается формулой

${\displaystyle {\mathfrak {so}}(n)={\mathfrak {o}}(n)=\left\{X\in M_{n}(\mathbb {R} )\mid X=-X^{\mathsf {T}}\right\},}$

и — пространство кососимметричных матриц размерности n , см. классическую группу , где o ( n ) — алгебра Ли O( n ) , ортогональная группа . Для справки, наиболее распространенным основанием для этого (3) является

${\displaystyle L_{\mathbf {x} }={\begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix}},\quad L_{\mathbf {y} }={\begin{bmatrix}0&0&1\\0&0&0\\-1&0&0\end{bmatrix}},\quad L_{\mathbf {z} }={\begin{bmatrix}0&-1&0\\1&0&0\\0&0&0\end{bmatrix}}.}$

Экспоненциальная карта

Соединение алгебры Ли с группой Ли представляет собой экспоненциальное отображение , которое определяется с помощью стандартного матричного ряда экспонент для e ^{A [8]} . Для любой кососимметричной матрицы A exp( A ) всегда является матрицей вращения. ^{[номер 3]}

Важным практическим примером является случай 3×3 . В группе вращений SO(3) показано, что каждый A ∈ so (3) можно отождествить с вектором Эйлера ω = θ u , где u = ( x , y , z ) — вектор единичной величины.

По свойствам отождествления u находится в нулевом пространстве A. Таким образом, u инвариантен слева согласно exp( A ) и, следовательно, является осью вращения. ${\displaystyle \mathbf {su} (2)\cong \mathbb {R} ^{3}}$

Согласно формуле вращения Родригеса в матричной форме получаем:

${\displaystyle {\begin{aligned}\exp(A)&=\exp {\bigl (}\theta (\mathbf {u} \cdot \mathbf {L} ){\bigr )}\\&=\exp \left({\begin{bmatrix}0&-z\theta &y\theta \\z\theta &0&-x\theta \\-y\theta &x\theta &0\end{bmatrix}}\right)\\&=I+\sin \theta \ \mathbf {u} \cdot \mathbf {L} +(1-\cos \theta )(\mathbf {u} \cdot \mathbf {L} )^{2},\end{aligned}}}$

где

${\displaystyle \mathbf {u} \cdot \mathbf {L} ={\begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0\end{bmatrix}}.}$

Это матрица поворота вокруг оси u на угол θ . Более подробную информацию см. в экспоненциальной карте SO(3) .

Формула Бейкера – Кэмпбелла – Хаусдорфа

Формула BCH дает явное выражение для Z = log( e ^X e ^Y ) в терминах разложения в ряд вложенных коммутаторов X и Y. ^[9] Это общее расширение разворачивается как ^{[nb 4]}

${\displaystyle Z=C(X,Y)=X+Y+{\tfrac {1}{2}}[X,Y]+{\tfrac {1}{12}}{\bigl [}X,[X,Y]{\bigr ]}-{\tfrac {1}{12}}{\bigl [}Y,[X,Y]{\bigr ]}+\cdots .}$

В случае 3 × 3 общее бесконечное разложение имеет компактный вид ^[10]

${\displaystyle Z=\alpha X+\beta Y+\gamma [X,Y],}$

для подходящих коэффициентов тригонометрической функции, подробно описанных в формуле Бейкера-Кэмпбелла-Хаусдорфа для SO(3) .

В качестве группового тождества вышеизложенное справедливо для всех точных представлений , включая дублет (спинорное представление), которое является более простым. Таким образом, та же явная формула напрямую следует через матрицы Паули; см. вывод 2 × 2 для SU(2) . Для общего случая n × n можно использовать Ref. ^[11]

Спиновая группа

Группа Ли матриц вращения размера n × n , SO( n ) , не является односвязной , поэтому теория Ли говорит нам, что это гомоморфный образ универсальной накрывающей группы . Часто с покрывающей группой, которая в данном случае называется спиновой группой , обозначаемой Spin( n ) , работать проще и естественнее. ^[12]

В случае плоского вращения SO(2) топологически является кругом S ¹ . Его универсальная накрывающая группа Spin(2) изоморфна вещественной прямой R при сложении. При использовании углов произвольной величины пользуются удобством универсального покрытия. Каждая матрица вращения 2 × 2 состоит из счетной бесконечности углов, разделенных целыми числами, кратными 2 π . Соответственно, фундаментальная группа SO (2) изоморфна целым числам Z .

В случае пространственных вращений SO(3) топологически эквивалентно трехмерному реальному проективному пространству RP ³ . ^{Его универсальная} накрывающая группа Spin( 3 ) изоморфна 3-сфере S3 . Каждая матрица вращения 3 × 3 создается двумя противоположными точками на сфере. Соответственно, фундаментальная группа SO(3) изоморфна двухэлементной группе Z ₂ .

Мы также можем описать Spin(3) как изоморфный кватернионам единичной нормы при умножении, или некоторым вещественным матрицам 4 × 4 , или комплексным специальным унитарным матрицам 2 × 2 , а именно SU(2). Отображения покрытия для первого и последнего случая имеют вид

${\displaystyle \mathbb {H} \supset \{q\in \mathbb {H} :\|q\|=1\}\ni w+\mathbf {i} x+\mathbf {j} y+\mathbf {k} z\mapsto {\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}}\in \mathrm {SO} (3),}$

и

${\displaystyle \mathrm {SU} (2)\ni {\begin{bmatrix}\alpha &\beta \\-{\overline {\beta }}&{\overline {\alpha }}\end{bmatrix}}\mapsto {\begin{bmatrix}{\frac {1}{2}}\left(\alpha ^{2}-\beta ^{2}+{\overline {\alpha ^{2}}}-{\overline {\beta ^{2}}}\right)&{\frac {i}{2}}\left(-\alpha ^{2}-\beta ^{2}+{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&-\alpha \beta -{\overline {\alpha }}{\overline {\beta }}\\{\frac {i}{2}}\left(\alpha ^{2}-\beta ^{2}-{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&{\frac {i}{2}}\left(\alpha ^{2}+\beta ^{2}+{\overline {\alpha ^{2}}}+{\overline {\beta ^{2}}}\right)&-i\left(+\alpha \beta -{\overline {\alpha }}{\overline {\beta }}\right)\\\alpha {\overline {\beta }}+{\overline {\alpha }}\beta &i\left(-\alpha {\overline {\beta }}+{\overline {\alpha }}\beta \right)&\alpha {\overline {\alpha }}-\beta {\overline {\beta }}\end{bmatrix}}\in \mathrm {SO} (3).}$

Подробное описание SU(2)-накрытия и кватернионного накрытия см. в спиновой группе SO(3) .

Многие особенности этих случаев одинаковы для более высоких размерностей. Все накрытия являются взаимно-однозначными, причем SO ( n ) , n > 2 , имеют фундаментальную группу Z2 _. Естественная обстановка для этих групп находится внутри алгебры Клиффорда . Один тип действия вращений представляет собой своеобразный «сэндвич», обозначаемый qvq ^∗ . Что еще более важно в приложениях к физике, соответствующее спиновое представление алгебры Ли находится внутри алгебры Клиффорда. Его можно возвести в степень обычным способом, чтобы получить двузначное представление, также известное как проективное представление группы вращения. Так обстоит дело с SO(3) и SU(2), где двузначное представление можно рассматривать как «обратное» накрывающему отображению. По свойствам накрывающих отображений обратное можно выбрать однозначно как локальное сечение, но не глобально.

Бесконечно малые вращения

Матрицы в алгебре Ли сами по себе не являются вращениями; кососимметричные матрицы являются производными, пропорциональными разностями вращений. Фактическое «дифференциальное вращение» или бесконечно малая матрица вращения имеет форму

${\displaystyle I+A\,d\theta ,}$

где dθ исчезающе мало и A ∈ so (n) , например, с A = L _x ,

${\displaystyle dL_{x}={\begin{bmatrix}1&0&0\\0&1&-d\theta \\0&d\theta &1\end{bmatrix}}.}$

Правила вычислений такие же, как обычно, за исключением того, что бесконечно малые величины второго порядка обычно отбрасываются. Согласно этим правилам, эти матрицы не удовлетворяют всем тем же свойствам, что и обычные матрицы конечного вращения при обычном подходе к бесконечно малым числам. ^[13] Оказывается, порядок применения бесконечно малых вращений не имеет значения . Чтобы увидеть это на примере, обратитесь к бесконечно малым вращениям SO(3) .

Конверсии

Мы видели существование нескольких разложений, которые применимы в любом измерении, а именно: независимые плоскости, последовательные углы и вложенные измерения. Во всех этих случаях мы можем либо разложить матрицу, либо построить ее. Мы также уделили особое внимание матрицам вращения 3 × 3 , и они требуют дальнейшего внимания в обоих направлениях (Stuelpnagel 1964).

Кватернион

Учитывая единичный кватернион q = w + x i + y j + z k , эквивалентная предварительно умноженная (для использования с векторами-столбцами) матрица вращения 3 × 3 равна ^[14]

${\displaystyle Q={\begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}\end{bmatrix}}.}$

Теперь каждый компонент кватерниона оказывается умноженным на два в члене второй степени, и если все такие члены равны нулю, то остается единичная матрица. Это приводит к эффективному и надежному преобразованию любого кватерниона – единичного или неединичного – в матрицу вращения 3 × 3 . Данный:

${\displaystyle {\begin{aligned}n&=w\times w+x\times x+y\times y+z\times z\\s&={\begin{cases}0&{\text{if }}n=0\\{\frac {2}{n}}&{\text{otherwise}}\end{cases}}\\\end{aligned}}}$

мы можем рассчитать

${\displaystyle Q={\begin{bmatrix}1-s(yy+zz)&s(xy-wz)&s(xz+wy)\\s(xy+wz)&1-s(xx+zz)&s(yz-wx)\\s(xz-wy)&s(yz+wx)&1-s(xx+yy)\end{bmatrix}}}$

Освободившись от требования единичного кватерниона, мы обнаруживаем, что ненулевые кватернионы действуют как однородные координаты для матриц вращения 3 × 3 . Преобразование Кэли, обсуждавшееся ранее, получается путем масштабирования кватерниона так, чтобы его компонент w был равен 1. При повороте на 180 ° вокруг любой оси w будет равно нулю, что объясняет ограничение Кэли.

Сумма элементов по главной диагонали ( следу ) плюс один равна 4 − 4( x ² + y ² + z ² ) , что равно 4 w ² . Таким образом, мы можем записать сам след как 2 w ² + 2 w ² − 1 ; а из предыдущей версии матрицы мы видим, что сами диагональные элементы имеют тот же вид: 2 x ² + 2 w ² − 1 , 2 y ² + 2 w ² − 1 и 2 z ² + 2 w ² − 1. . Таким образом, мы можем легко сравнить величины всех четырех компонентов кватернионов, используя диагональ матрицы. Фактически мы можем получить все четыре величины, используя суммы и квадратные корни, и выбрать согласованные знаки, используя кососимметричную часть недиагональных записей:

${\displaystyle {\begin{aligned}t&=\operatorname {tr} Q=Q_{xx}+Q_{yy}+Q_{zz}\quad ({\text{the trace of }}Q)\\r&={\sqrt {1+t}}\\w&={\tfrac {1}{2}}r\\x&=\operatorname {sgn} \left(Q_{zy}-Q_{yz}\right)\left|{\tfrac {1}{2}}{\sqrt {1+Q_{xx}-Q_{yy}-Q_{zz}}}\right|\\y&=\operatorname {sgn} \left(Q_{xz}-Q_{zx}\right)\left|{\tfrac {1}{2}}{\sqrt {1-Q_{xx}+Q_{yy}-Q_{zz}}}\right|\\z&=\operatorname {sgn} \left(Q_{yx}-Q_{xy}\right)\left|{\tfrac {1}{2}}{\sqrt {1-Q_{xx}-Q_{yy}+Q_{zz}}}\right|\end{aligned}}}$

Альтернативно, используйте один квадратный корень и деление

${\displaystyle {\begin{aligned}t&=\operatorname {tr} Q=Q_{xx}+Q_{yy}+Q_{zz}\\r&={\sqrt {1+t}}\\s&={\tfrac {1}{2r}}\\w&={\tfrac {1}{2}}r\\x&=\left(Q_{zy}-Q_{yz}\right)s\\y&=\left(Q_{xz}-Q_{zx}\right)s\\z&=\left(Q_{yx}-Q_{xy}\right)s\end{aligned}}}$

Это численно стабильно до тех пор, пока след t не является отрицательным; в противном случае мы рискуем разделить на (почти) ноль. В этом случае предположим, что Q _xx — это наибольшая диагональная запись, поэтому x будет иметь наибольшую величину (остальные случаи получаются путем циклической перестановки); тогда следующее безопасно.

${\displaystyle {\begin{aligned}r&={\sqrt {1+Q_{xx}-Q_{yy}-Q_{zz}}}\\s&={\tfrac {1}{2r}}\\w&=\left(Q_{zy}-Q_{yz}\right)s\\x&={\tfrac {1}{2}}r\\y&=\left(Q_{xy}+Q_{yx}\right)s\\z&=\left(Q_{zx}+Q_{xz}\right)s\end{aligned}}}$

Если матрица содержит значительную ошибку, например накопленную числовую ошибку, мы можем построить симметричную матрицу 4 × 4 :

${\displaystyle K={\frac {1}{3}}{\begin{bmatrix}Q_{xx}-Q_{yy}-Q_{zz}&Q_{yx}+Q_{xy}&Q_{zx}+Q_{xz}&Q_{zy}-Q_{yz}\\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{xz}-Q_{zx}\\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{yx}-Q_{xy}\\Q_{zy}-Q_{yz}&Q_{xz}-Q_{zx}&Q_{yx}-Q_{xy}&Q_{xx}+Q_{yy}+Q_{zz}\end{bmatrix}},}$

и найдите собственный вектор ( x , y , z , w ) его собственного значения наибольшей величины. (Если Q действительно является матрицей вращения, это значение будет равно 1.) Полученный таким образом кватернион будет соответствовать матрице вращения, наиболее близкой к данной матрице (Бар-Ицхак 2000) (Примечание: формулировка цитируемой статьи умножается после умножения, работает с векторами-строками).

Полярное разложение

Если матрица M размера n × n невырождена, ее столбцы представляют собой линейно независимые векторы; таким образом, процесс Грама – Шмидта может превратить их в ортонормированный базис. С точки зрения числовой линейной алгебры , мы преобразуем M в ортогональную матрицу Q , используя QR-разложение . Однако мы часто предпочитаем Q, ближайший к M , чего этот метод не обеспечивает. Для этого нам нужен инструмент полярного разложения (Fan & Hoffman 1955; Higham 1989).

Для измерения близости мы можем использовать любую матричную норму, инвариантную относительно ортогональных преобразований. Удобным выбором является норма Фробениуса ‖ Q − M ‖ _F в квадрате, которая представляет собой сумму квадратов разностей элементов. Написав это в терминах трассировки Tr , наша цель:

Найдите Q, минимизирующее Tr( ( Q - M ) ^T ( Q - M ) ) , при условии Q ^T Q знак равно I .

Хотя целевая функция записана в матричных терминах, она представляет собой всего лишь квадратичный полином. Мы можем минимизировать его обычным способом, найдя, где его производная равна нулю. Для матрицы 3 × 3 ограничение ортогональности подразумевает шесть скалярных равенств, которым должны удовлетворять элементы Q. Чтобы включить ограничение(я), мы можем использовать стандартный метод — множители Лагранжа , собранные в виде симметричной матрицы Y. Таким образом, наш метод:

Дифференцируем Tr( ( Q - M ) ^T ( Q - M ) + ( Q ^T Q - I ) Y ) по (элементам) Q и приравниваем нулю.

Рассмотрим пример 2×2 . Включая ограничения, мы стремимся свести к минимуму

${\displaystyle {\begin{aligned}&\left(Q_{xx}-M_{xx}\right)^{2}+\left(Q_{xy}-M_{xy}\right)^{2}+\left(Q_{yx}-M_{yx}\right)^{2}+\left(Q_{yy}-M_{yy}\right)^{2}\\&\quad {}+\left(Q_{xx}^{2}+Q_{yx}^{2}-1\right)Y_{xx}+\left(Q_{xy}^{2}+Q_{yy}^{2}-1\right)Y_{yy}+2\left(Q_{xx}Q_{xy}+Q_{yx}Q_{yy}\right)Y_{xy}.\end{aligned}}}$

Взяв производную по Q _xx , Q _xy , Q _yx , Q _yy по очереди, собираем матрицу.

${\displaystyle 2{\begin{bmatrix}Q_{xx}-M_{xx}+Q_{xx}Y_{xx}+Q_{xy}Y_{xy}&Q_{xy}-M_{xy}+Q_{xx}Y_{xy}+Q_{xy}Y_{yy}\\Q_{yx}-M_{yx}+Q_{yx}Y_{xx}+Q_{yy}Y_{xy}&Q_{yy}-M_{yy}+Q_{yx}Y_{xy}+Q_{yy}Y_{yy}\end{bmatrix}}}$

В общем случае получаем уравнение

${\displaystyle 0=2(Q-M)+2QY,}$

так что

${\displaystyle M=Q(I+Y)=QS,}$

где Q ортогонален, а S симметричен. Чтобы гарантировать минимум, матрица Y (и, следовательно, S ) должна быть положительно определенной. В линейной алгебре QS называется полярным разложением M , где S - положительным квадратным корнем из S ² = M ^T M .

${\displaystyle S^{2}=\left(Q^{\mathsf {T}}M\right)^{\mathsf {T}}\left(Q^{\mathsf {T}}M\right)=M^{\mathsf {T}}QQ^{\mathsf {T}}M=M^{\mathsf {T}}M}$

Когда M несингулярно , факторы Q и S полярного разложения определяются однозначно . Однако определитель S положителен, поскольку S положительно определен, поэтому Q наследует знак определителя M . То есть Q гарантированно будет только ортогональной, а не матрицей вращения. Это неизбежно; M с отрицательным определителем не имеет однозначно определенной матрицы ближайшего вращения.

Ось и угол

Чтобы эффективно построить матрицу вращения Q по углу θ и единичной оси u , мы можем воспользоваться преимуществами симметрии и кососимметрии внутри записей. Если x , y и z являются компонентами единичного вектора, представляющего ось, и

${\displaystyle {\begin{aligned}c&=\cos \theta \\s&=\sin \theta \\C&=1-c\end{aligned}}}$

затем

${\displaystyle Q(\theta )={\begin{bmatrix}xxC+c&xyC-zs&xzC+ys\\yxC+zs&yyC+c&yzC-xs\\zxC-ys&zyC+xs&zzC+c\end{bmatrix}}}$

Определение оси и угла, как и определение кватерниона, возможно только с точностью до знака; то есть ( u , θ ) и (− u , − θ ) соответствуют одной и той же матрице вращения, точно так же, как q и − q . Кроме того, извлечение оси и угла представляет дополнительные трудности. Угол может быть ограничен диапазоном от 0° до 180°, но формально углы кратны 360°. Когда угол равен нулю, ось не определена. Когда угол равен 180°, матрица становится симметричной, что влияет на извлечение оси. Вблизи кратных 180° необходимо соблюдать осторожность, чтобы избежать числовых проблем: при извлечении угла арктангенс с двумя аргументами с atan2 (sin θ , cos θ ) , равным θ , позволяет избежать нечувствительности arccos; а при вычислении величины оси для получения единичной величины метод грубой силы может потерять точность из-за потери значения (Moler & Morrison 1983).

Частичный подход заключается в следующем:

${\displaystyle {\begin{aligned}x&=Q_{zy}-Q_{yz}\\y&=Q_{xz}-Q_{zx}\\z&=Q_{yx}-Q_{xy}\\r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\t&=Q_{xx}+Q_{yy}+Q_{zz}\\\theta &=\operatorname {atan2} (r,t-1)\end{aligned}}}$

Тогда x- , y- и z - компоненты оси будут разделены на r . Полностью надежный подход будет использовать другой алгоритм, когда t , след матрицы Q , отрицательный, как при извлечении кватернионов. Когда r равно нулю, поскольку угол равен нулю, ось должна быть получена из какого-то источника, отличного от матрицы.

углы Эйлера

Сложность преобразования возрастает с увеличением углов Эйлера (используемых здесь в широком смысле). Первая трудность состоит в том, чтобы установить, какой из двадцати четырех вариантов декартова порядка осей мы будем использовать. Предположим, что тремя углами являются θ ₁ , θ ₂ , θ ₃ ; физика и химия могут интерпретировать их как

${\displaystyle Q(\theta _{1},\theta _{2},\theta _{3})=Q_{\mathbf {z} }(\theta _{1})Q_{\mathbf {y} }(\theta _{2})Q_{\mathbf {z} }(\theta _{3}),}$

в то время как динамика самолета может использовать

${\displaystyle Q(\theta _{1},\theta _{2},\theta _{3})=Q_{\mathbf {z} }(\theta _{3})Q_{\mathbf {y} }(\theta _{2})Q_{\mathbf {x} }(\theta _{1}).}$

Один системный подход начинается с выбора самой правой оси. Среди всех перестановок ( x , y , z ) только две помещают эту ось на первое место; одна перестановка четная, а другая нечетная. Таким образом, выбор паритета устанавливает среднюю ось. Это оставляет два варианта для самой левой оси: либо дублировать первую, либо нет. Эти три варианта дают нам 3 × 2 × 2 = 12 вариантов; мы удваиваем это число до 24, выбирая статические или вращающиеся оси.

Этого достаточно, чтобы построить матрицу из углов, но тройки, различающиеся во многом, могут дать одну и ту же матрицу вращения. Например, предположим, что мы используем соглашение zyz , указанное выше; то мы имеем следующие эквивалентные пары:

Углы для любого порядка можно найти, используя краткую стандартную процедуру (Herter & Lott 1993; Shoemake 1994).

Проблема сингулярного выравнивания, математического аналога физической блокировки подвеса , возникает, когда среднее вращение выравнивает оси первого и последнего поворотов. Это влияет на каждый порядок оси при четном или нечетном кратном 90°. Эти особенности не характерны для матрицы вращения как таковой и возникают только при использовании углов Эйлера.

Сингулярностей можно избежать, если рассматривать матрицу вращения и манипулировать ею как ортонормированные векторы-строки (в 3D-приложениях часто называемые правым вектором, восходящим вектором и исходящим вектором), а не как углы. Сингулярностей также можно избежать при работе с кватернионами.

Вектор-векторная формулировка

В некоторых случаях интересно описать вращение, указав, как один вектор отображается в другой по кратчайшему пути (наименьшему углу). При этом полностью описывается связанная матрица вращения. В общем случае, учитывая x , y ∈ ⁿ , матрица ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {S} }$

${\displaystyle R:=I+yx^{\mathsf {T}}-xy^{\mathsf {T}}+{\frac {1}{1+\langle x,y\rangle }}\left(yx^{\mathsf {T}}-xy^{\mathsf {T}}\right)^{2}}$

принадлежит SO( n + 1) и отображает x в y . ^[15]

Равномерные матрицы случайного вращения

Иногда нам необходимо создать равномерно распределенную матрицу случайного вращения. В двух измерениях интуитивно кажется очевидным, что это означает, что угол поворота равномерно распределен между 0 и 2 π . Эта интуиция верна, но не переносится на более высокие измерения. Например, если мы разложим матрицы вращения 3 × 3 в форме ось-угол, угол не должен распределяться равномерно; вероятность того, что (величина) угла не превышает θ, должна быть равна1/π( θ - грех θ ) , ибо 0 ≤ θ ≤ π .

Поскольку SO( n ) — связная и локально компактная группа Ли, у нас есть простой стандартный критерий равномерности, а именно, что распределение остается неизменным при составлении с любым произвольным вращением («перенос» группы Ли). Это определение соответствует так называемой мере Хаара . Леон, Массе и Ривест (2006) показывают, как использовать преобразование Кэли для создания и проверки матриц в соответствии с этим критерием.

Мы также можем создать равномерное распределение в любом измерении, используя алгоритм подгруппы Диакониса и Шахшахани (1987). При этом рекурсивно используется структура вложенной группы измерений SO( n ) следующим образом. Создайте равномерный угол и постройте матрицу вращения 2 × 2 . Чтобы перейти от n к n + 1 , сгенерируйте вектор v, равномерно распределенный на n -сфере S ⁿ , вставьте матрицу n × n в следующий больший размер с последним столбцом (0, ..., 0, 1) и поверните большую матрицу, чтобы последний столбец стал v .

Как обычно, у нас есть специальные альтернативы для случая 3×3 . Каждый из этих методов начинается с трех независимых случайных скаляров, равномерно распределенных на единичном интервале. Арво (1992) использует нечетное измерение, чтобы изменить отражение Хаусхолдера на вращение путем отрицания, и использует это для нацеливания оси равномерного плоского вращения.

Другой метод использует единичные кватернионы. Умножение матриц вращения гомоморфно умножению кватернионов, а умножение на единичный кватернион вращает единичную сферу. ^{Поскольку} гомоморфизм является локальной изометрией , мы сразу заключаем, что для получения равномерного распределения на SO(3) мы можем использовать равномерное распределение на S3 . На практике: создайте четырехэлементный вектор, где каждый элемент представляет собой выборку нормального распределения. Нормализуйте его длину, и вы получите случайный единичный кватернион с равномерной выборкой, который представляет случайное вращение с равномерной выборкой. Обратите внимание, что вышесказанное применимо только к вращениям в измерении 3. Для получения обобщенного представления о кватернионах следует изучить Роторы .

Углы Эйлера также можно использовать, хотя и не каждый угол распределен равномерно (Murnaghan 1962; Miles 1965).

Для формы «ось-угол» ось равномерно распределена по единичной сфере направлений S ² , тогда как угол имеет неравномерное распределение по [0, π ] , отмеченное ранее (Miles 1965).

Смотрите также

• Формула Эйлера – Родригеса
• Теорема Эйлера о вращении
• Формула вращения Родригеса
• Плоскость вращения
• Представление оси-угла
• Группа ротации SO(3)
• Формализмы вращения в трех измерениях
• Оператор вращения (векторное пространство)
• Матрица трансформации
• Система рыскания-тангажа-крена
• Алгоритм Кабша
• Изометрия
• Жесткая трансформация
• Вращения в 4-мерном евклидовом пространстве
• Тригонометрические тождества
• Версор

Примечания

1. Обратите внимание, что если вместо вращения векторов вращается система отсчета, знаки в терминах sin θ поменяются местами. Если система отсчета A повернута против часовой стрелки вокруг начала координат на угол θ , чтобы создать систему отсчета B, то R _x (с перевернутыми знаками) преобразует вектор, описанный в координатах системы отсчета A, в координаты системы отсчета B. Преобразования системы координат в аэрокосмической, робототехнике и других областях часто выполняются с использованием такой интерпретации матрицы вращения.
2. Обратите внимание, что

   ${\displaystyle \mathbf {u} \otimes \mathbf {u} ={\bigl (}[\mathbf {u} ]_{\times }{\bigr )}^{2}+{\mathbf {I} }}$

   так что в обозначениях Родригеса, что эквивалентно,

   ${\displaystyle \mathbf {R} =\mathbf {I} +(\sin \theta )[\mathbf {u} ]_{\times }+(1-\cos \theta ){\bigl (}[\mathbf {u} ]_{\times }{\bigr )}^{2}.}$

3. Обратите внимание, что это экспоненциальное отображение кососимметричных матриц в матрицы вращения сильно отличается от преобразования Кэли, обсуждавшегося ранее, и отличается до третьего порядка,

   ${\displaystyle e^{2A}-{\frac {I+A}{I-A}}=-{\tfrac {2}{3}}A^{3}+\mathrm {O} \left(A^{4}\right).}$

   И наоборот, кососимметричная матрица A , задающая матрицу вращения через карту Кэли, задает ту же матрицу вращения через карту exp(2 artanh A ) .
4. Подробный вывод см. в разделе «Производная экспоненциальной карты» . Вопросы сходимости этого ряда к правому элементу алгебры Ли здесь оставлены под ковром. Сходимость гарантируется, когда ‖ X ‖ + ‖ Y ‖ < log 2 и ‖ Z ‖ < log 2 . Если эти условия не выполняются, ряд все равно может сходиться. Решение всегда существует, поскольку ^{в рассматриваемых случаях} требуется уточнение .

Примечания

1. Своковски, Эрл (1979). Исчисление с аналитической геометрией (второе изд.). Бостон: Приндл, Вебер и Шмидт. ISBN 0-87150-268-2.
2. Рекомендация W3C (2003 г.). «Масштабируемая векторная графика – исходная система координат».{{cite web}}: CS1 maint: numeric names: authors list (link)
3. «Матрицы вращения» (PDF) . Проверено 30 ноября 2021 г.
4. Куо Кан, Лян (6 октября 2018 г.). «Эффективное преобразование вращающейся матрицы в ось и угол вращения путем расширения формулы Родригеса». arXiv : 1810.02999 [cs.CG].
5. Тейлор, Камилло Дж.; Кригман, Дэвид Дж. (1994). «Минимизация группы Ли SO (3) и связанных с ней многообразий» (PDF) . Технический отчет № 9405 . Йельский университет.
6. Коул, Ян Р. (январь 2015 г.). Моделирование CPV (дипломная работа). Университет Лафборо. hdl : 2134/18050.
7. Бейкер (2003); Фултон и Харрис (1991)
8. (Веддерберн, 1934, §8.02)
9. Холл 2004, гл. 3; Варадараджан 1984, §2.15
10. (Энгё, 2001)
11. Куртрайт, TL ; Фэрли, Д.Б. ; Захос, СК (2014). «Компактная формула для вращений как полиномов матрицы спина». СИГМА . 10 : 084.arXiv : 1402.3541 . Бибкод : 2014SIGMA..10..084C. дои : 10.3842/SIGMA.2014.084. S2CID  18776942.
12. Бейкер 2003, гл. 5; Фултон и Харрис 1991, стр. 299–315.
13. (Гольдштейн, Пул и Сафко 2002, §4.8)
14. Шумейк, Кен (1985). «Анимация вращения с помощью кватернионных кривых». Компьютерная графика: материалы конференции SIGGRAPH '85. SIGGRAPH '85, 22–26 июля 1985 г., Сан-Франциско. Том. 19. Ассоциация вычислительной техники. стр. 245–254. дои : 10.1145/325334.325242 . ISBN 0897911660.
15. Сид, Хосе Анхель; Тохо, Ф. Адриан Ф. (2018). «Условие Липшица вдоль трансверсального слоения подразумевает локальную единственность ОДУ». Электронный журнал качественной теории дифференциальных уравнений . 13 (13): 1–14. arXiv : 1801.01724 . дои : 10.14232/ejqtde.2018.1.13 .

Рекомендации

• Арво, Джеймс (1992), «Матрицы быстрого случайного вращения», Дэвид Кирк (редактор), Graphics Gems III, Сан-Диего: Academic Press Professional, стр. 117–120, Bibcode : 1992grge.book.....K , ISBN 978-0-12-409671-4
• Бейкер, Эндрю (2003), Матричные группы: введение в теорию групп Ли , Springer , ISBN 978-1-85233-470-3
• Бар-Ицхак, Ицхак Ю. (ноябрь – декабрь 2000 г.), «Новый метод извлечения кватерниона из матрицы вращения», Journal of Guidance, Control and Dynamics , 23 (6): 1085–1087, Bibcode : 2000JGCD ... 23.1085B, номер домена : 10.2514/2.4654, ISSN  0731-5090
• Бьорк, Оке; Боуи, Клазетт (июнь 1971 г.), «Итеративный алгоритм для вычисления наилучшей оценки ортогональной матрицы», SIAM Journal on Numerical Analysis , 8 (2): 358–364, Bibcode : 1971SJNA....8..358B, doi : 10.1137/0708036, ISSN  0036-1429
• Кэли, Артур (1846), «Sur quelques proprietés des déterminants gauches», Journal für die reine und angewandte Mathematik , 1846 (32): 119–123, doi : 10.1515/crll.1846.32.119, ISSN  0075-4102, S2CID  1995467 46; перепечатано как статья 52 в книге Кэли, Артур (1889), Сборник математических статей Артура Кэли, том. I (1841–1853), Cambridge University Press , стр. 332–336.
• Диаконис, Персия ; Шахшахани, Мехрдад (1987), «Алгоритм подгруппы для генерации однородных случайных величин», Вероятность в инженерных и информационных науках , 1 : 15–32, doi : 10.1017/S0269964800000255, ISSN  0269-9648, S2CID  122752374
• Энгё, Кент (июнь 2001 г.), «О формуле BCH в so (3)», BIT Numerical Mathematics , 41 (3): 629–632, doi : 10.1023/A: 1021979515229, ISSN  0006-3835, S2CID  126053191
• Фан, Кай; Хоффман, Алан Дж. (февраль 1955 г.), «Некоторые метрические неравенства в пространстве матриц», Труды Американского математического общества , 6 (1): 111–116, doi : 10.2307/2032662 , ISSN  0002-9939, JSTOR  2032662
• Фултон, Уильям ; Харрис, Джо (1991), Теория представлений: первый курс , Тексты для аспирантов по математике , том. 129, Нью-Йорк, Берлин, Гейдельберг: Springer , ISBN 978-0-387-97495-8, МР  1153249
• Гольдштейн, Герберт ; Пул, Чарльз П.; Сафко, Джон Л. (2002), Классическая механика (третье изд.), Аддисон Уэсли , ISBN 978-0-201-65702-9
• Холл, Брайан К. (2004), Группы Ли, алгебры Ли и представления: элементарное введение , Springer , ISBN 978-0-387-40122-5( ГТМ 222)
• Гертер, Томас; Лотт, Клаус (сентябрь – октябрь 1993 г.), «Алгоритмы разложения трехмерных ортогональных матриц на примитивные вращения», Computers & Graphics , 17 (5): 517–527, doi : 10.1016/0097-8493(93)90003-R , ISSN  0097-8493
• Хайэм, Николас Дж. (1 октября 1989 г.), «Проблемы и приложения близости матрицы», Говер, Майкл Дж. К.; Барнетт, Стивен (ред.), Приложения теории матриц, Oxford University Press , стр. 1–27, ISBN 978-0-19-853625-3
• Леон, Карлос А.; Массе, Жан-Клод; Ривест, Луи-Поль (февраль 2006 г.), «Статистическая модель случайного вращения», Journal of Multivariate Analysis , 97 (2): 412–430, doi : 10.1016/j.jmva.2005.03.009 , ISSN  0047-259X
• Майлз, Роджер Э. (декабрь 1965 г.), «О случайных вращениях в R ³ », Biometrika , 52 (3/4): 636–639, doi : 10.2307/2333716, ISSN  0006-3444, JSTOR  2333716.
• Молер, Клив ; Моррисон, Дональд (1983), «Замена квадратных корней суммами Пифагора», IBM Journal of Research and Development , 27 (6): 577–581, doi : 10.1147/rd.276.0577, ISSN  0018-8646
• Мурнаган, Фрэнсис Д. (1950), «Элемент объема группы вращения», Труды Национальной академии наук , 36 (11): 670–672, Бибкод : 1950PNAS...36..670M, doi : 10.1073/pnas.36.11.670 , ISSN  0027-8424, PMC  1063502 , PMID  16589056
• Мурнаган, Фрэнсис Д. (1962), Унитарные и ротационные группы , Лекции по прикладной математике, Вашингтон: Spartan Books
• Кэли, Артур (1889), Сборник математических статей Артура Кэли, том. I (1841–1853), Cambridge University Press , стр. 332–336.
• Пэт, Алан В. (1986), «Быстрый алгоритм общего вращения растра» (PDF) , Труды, Графический интерфейс '86 : 77–81
• Добеши, Ингрид ; Свелденс, Вим (1998), «Факторизация вейвлет-преобразований в шаги подъема» (PDF) , Journal of Fourier Analysis and Applications , 4 (3): 247–269, doi : 10.1007/BF02476026, S2CID  195242970
• Пике, Майкл Э. (1990), «Инструменты вращения», в Эндрю С. Гласснере (редактор), Graphics Gems, Сан-Диего: Academic Press Professional, стр. 465–469, ISBN 978-0-12-286166-6
• Пресс, Уильям Х.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007), «Раздел 21.5.2. Выбор матрицы случайного вращения», Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8, заархивировано из оригинала 11 августа 2011 г. , получено 18 августа 2011 г.

• Шепперд, Стэнли В. (май – июнь 1978 г.), «Кватернион из матрицы вращения», Journal of Guidance and Control , 1 (3): 223–224, doi : 10.2514/3.55767b
• Шумейк, Кен (1994), «Преобразование угла Эйлера», Пол Хекберт (редактор), Graphics Gems IV, Сан-Диего: Academic Press Professional, стр. 222–229, ISBN 978-0-12-336155-4
• Стуэльпнагель, Джон (октябрь 1964 г.), «О параметризации трехмерной группы вращения», SIAM Review , 6 (4): 422–430, Bibcode : 1964SIAMR...6..422S, doi : 10.1137/1006093, ISSN  0036-1445, S2CID  13990266(Также NASA-CR-53568.)
• Варадараджан, Виравалли С. (1984), Группы Ли, алгебры Ли и их представление , Springer , ISBN 978-0-387-90969-1( ГТМ 102)
• Веддерберн, Джозеф Х.М. (1934), Лекции по матрицам, AMS , ISBN 978-0-8218-3204-2

Внешние ссылки

• «Вращение», Математическая энциклопедия , EMS Press , 2001 [1994]
• Матрицы вращения в Mathworld
• Интерактивная демонстрация Math Awareness Month 2000 (требуется Java )
• Матрицы вращения на MathPages
• (на итальянском языке) Параметризация SOn(R) обобщенными углами Эйлера
• Вращение вокруг любой точки