Связь с Эхресманном

Построение дифференциальной геометрии на расслоениях волокон

В дифференциальной геометрии связность Эресмана (в честь французского математика Шарля Эресмана , который впервые формализовал это понятие) является версией понятия связности , которая имеет смысл на любом гладком расслоении . В частности, она не опирается на возможную структуру векторного расслоения базового расслоения, но тем не менее линейные связности можно рассматривать как частный случай. Другим важным частным случаем связностей Эресмана являются главные связности на главных расслоениях , которые должны быть эквивариантными относительно действия главной группы Ли .

Введение

Ковариантная производная в дифференциальной геометрии — это линейный дифференциальный оператор , который берет производную по направлению сечения векторного расслоения ковариантным образом . Он также позволяет сформулировать понятие параллельного сечения расслоения в направлении вектора: сечение s параллельно вдоль вектора , если . Таким образом, ковариантная производная предоставляет по крайней мере две вещи: дифференциальный оператор и понятие того, что значит быть параллельным в каждом направлении. Связность Эресмана полностью отбрасывает дифференциальный оператор и определяет связность аксиоматически в терминах сечений, параллельных в каждом направлении (Эресманн 1950). В частности, связность Эресмана выделяет векторное подпространство каждого касательного пространства к общему пространству расслоения волокон, называемое горизонтальным пространством . Тогда сечение горизонтально (т. е. параллельно) в направлении , если лежит в горизонтальном пространстве. Здесь мы рассматриваем как функцию от базы к расслоению волокон , так что тогда это проталкивание касательных векторов. Горизонтальные пространства вместе образуют векторное подрасслоение . ${\displaystyle X}$ ${\displaystyle \nabla _{X}s=0}$ ${\displaystyle s}$ ${\displaystyle X}$ ${\displaystyle {\rm {d}}s(X)}$ ${\displaystyle s}$ ${\displaystyle s\colon M\to E}$ ${\displaystyle M}$ ${\displaystyle E}$ ${\displaystyle {\rm {d}}s\colon TM\to TE}$ ${\displaystyle TE}$

Это имеет непосредственное преимущество в том, что может быть определено на гораздо более широком классе структур, чем простые векторные расслоения. В частности, оно хорошо определено на общем расслоении волокон . Более того, многие из особенностей ковариантной производной все еще остаются: параллельный перенос, кривизна и голономия .

Недостающим компонентом связи, помимо линейности, является ковариантность . В классических ковариантных производных ковариантность является апостериорным свойством производной. При их построении указывается закон преобразования символов Кристоффеля  , который не является ковариантным, и тогда общая ковариантность производной следует как результат. Для связи Эресмана можно наложить обобщенный принцип ковариантности с самого начала, введя группу Ли, действующую на волокнах расслоения волокон. Соответствующее условие состоит в том, чтобы потребовать, чтобы горизонтальные пространства были, в определенном смысле, эквивариантны относительно действия группы.

Последний штрих для связности Эресмана заключается в том, что она может быть представлена ​​в виде дифференциальной формы , во многом таким же образом, как и в случае формы связи . Если группа действует на волокна и связь является эквивариантной, то форма также будет эквивариантной. Более того, форма связи допускает определение кривизны как формы кривизны .

Формальное определение

Связность Эресмана — это выбор горизонтального подпространства для каждого , где — некоторое расслоение волокон, обычно главное расслоение . ${\displaystyle H_{p}\subset T_{p}P}$ ${\displaystyle p\in P}$ ${\displaystyle P}$

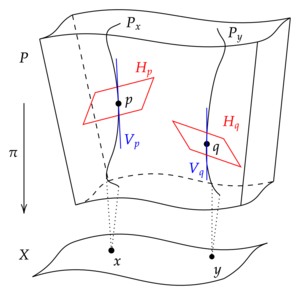
Пусть будет гладким расслоением . ^[1] Пусть ${\displaystyle \pi \colon E\to M}$

${\displaystyle V=\ker(\operatorname {d} \pi \colon TE\to TM)}$

быть вертикальным расслоением, состоящим из векторов, «касательных к волокнам» E , т.е. волокно V в точке равно . Это подрасслоение канонически определено даже тогда, когда нет канонического подпространства, касательного к базовому пространству M . (Разумеется, эта асимметрия исходит из самого определения расслоения, которое «имеет только одну проекцию», в то время как произведение имело бы две.) ${\displaystyle e\in E}$ ${\displaystyle V_{e}=T_{e}(E_{\pi (e)})}$ ${\displaystyle TE}$ ${\displaystyle \pi \colon E\to M}$ ${\displaystyle E=M\times F}$

Определение через горизонтальные подпространства

Связность Эресмана на — это гладкое подрасслоение , называемое горизонтальным расслоением связности, которое является дополнительным к V в том смысле, что оно определяет разложение в прямую сумму . ^[2] Более подробно, горизонтальное расслоение обладает следующими свойствами. ${\displaystyle E}$ ${\displaystyle H}$ ${\displaystyle TE}$ ${\displaystyle TE=H\oplus V}$

• Для каждой точки есть векторное подпространство касательного пространства к точке , называемое горизонтальным подпространством связности в точке . ${\displaystyle e\in E}$ ${\displaystyle H_{e}}$ ${\displaystyle T_{e}E}$ ${\displaystyle E}$ ${\displaystyle e}$ ${\displaystyle e}$
• ${\displaystyle H_{e}}$плавно зависит от . ${\displaystyle e}$
• Для каждого , . ${\displaystyle e\in E}$ ${\displaystyle H_{e}\cap V_{e}=\{0\}}$
• Любой касательный вектор в (для любого ) является суммой горизонтальной и вертикальной составляющей, так что . ${\displaystyle T_{e}E}$ ${\displaystyle e\in E}$ ${\displaystyle T_{e}E=H_{e}+V_{e}}$

В более сложных терминах такое задание горизонтальных пространств, удовлетворяющее этим свойствам, в точности соответствует гладкому сечению струйного расслоения J ¹ E → E .

Определение через форму подключения

Эквивалентно, пусть Φ будет проекцией на вертикальное расслоение V вдоль H (так что H = ker Φ ). Это определяется приведенным выше прямым разложением суммы TE на горизонтальную и вертикальную части и иногда называется формой связности Эресмана. Таким образом, Φ является гомоморфизмом векторного расслоения из TE в себя со следующими свойствами (проекций в целом):

• Ф ² = Ф ;
• Φ — тождество на V =Im Φ .

Наоборот, если Φ — эндоморфизм векторного расслоения TE , удовлетворяющий этим двум свойствам, то H = ker Φ — горизонтальное подрасслоение связности Эресмана.

Наконец, отметим, что Φ , будучи линейным отображением каждого касательного пространства в себя, может также рассматриваться как TE -значная 1-форма на E. Это будет полезной перспективой в следующих разделах.

Параллельная транспортировка с помощью горизонтальных подъемников

Связность Эресмана также предписывает способ подъема кривых из базового многообразия M в общее пространство расслоения волокон E таким образом, чтобы касательные к кривой были горизонтальными. ^{[2] [3]} Эти горизонтальные подъемы являются прямым аналогом параллельного переноса для других версий формализма связности.

В частности, предположим, что γ ( t ) — гладкая кривая в M, проходящая через точку x  =  γ (0). Пусть e  ∈  E _x — точка в слое над x . Подъем γ через e — это кривая в общем пространстве E такая, что ${\displaystyle {\tilde {\gamma }}(t)}$

${\displaystyle {\tilde {\gamma }}(0)=e}$, и ${\displaystyle \pi ({\tilde {\gamma }}(t))=\gamma (t).}$

Лифт является горизонтальным , если, кроме того, каждая касательная к кривой лежит в горизонтальном подрасслоении TE :

${\displaystyle {\tilde {\gamma }}'(t)\in H_{{\tilde {\gamma }}(t)}.}$

Можно показать, используя теорему о ранге–нуле, примененную к π и Φ , что каждый вектор X ∈ T _x M имеет единственный горизонтальный лифт до вектора . В частности, касательное поле к γ порождает горизонтальное векторное поле в полном пространстве расслоения γ * E . По теореме Пикара–Линделёфа это векторное поле интегрируемо . Таким образом, для любой кривой γ и точки e над x  =  γ (0) существует единственный горизонтальный лифт γ через e для малого времени t . ${\displaystyle {\tilde {X}}\in T_{e}E}$

Обратите внимание, что для общих связностей Эресмана горизонтальный подъем зависит от пути. Когда две гладкие кривые в M , совпадающие в γ ₁ (0) =  γ ₂ (0) =  x ₀ и также пересекающиеся в другой точке x ₁  ∈  M , поднимаются горизонтально в E через ту же самую e  ∈  π ⁻¹ ( x ₀ ), они, как правило, проходят через разные точки π ⁻¹ ( x ₁ ). Это имеет важные последствия для дифференциальной геометрии расслоений: пространство сечений H не является подалгеброй Ли пространства векторных полей на E , поскольку оно (в общем случае) не замкнуто относительно скобки Ли векторных полей . Эта неспособность замкнуться относительно скобки Ли измеряется кривизной .

Характеристики

Кривизна

Пусть Φ — связность Эресмана. Тогда кривизна Φ определяется как ^[2]

${\displaystyle R={\tfrac {1}{2}}[\varPhi ,\varPhi ]}$

где [-,-] обозначает скобку Фрёлихера-Нийенхейса Φ ∈ Ω ¹ ( E , TE ) с собой. Таким образом, R ∈ Ω ² ( E , TE ) — это двумерная форма на E со значениями в TE , определяемая как

${\displaystyle R(X,Y)=\varPhi \left([(\mathrm {id} -\varPhi )X,(\mathrm {id} -\varPhi )Y]\right)}$,

или, другими словами,

${\displaystyle R\left(X,Y\right)=\left[X_{H},Y_{H}\right]_{V}}$,

где X = X _H + X _V обозначает разложение прямой суммы на компоненты H и V соответственно. Из этого последнего выражения для кривизны видно, что она тождественно равна нулю тогда и только тогда, когда горизонтальное подрасслоение интегрируемо по Фробениусу . Таким образом , кривизна является условием интегрируемости для горизонтального подрасслоения, чтобы дать поперечные сечения расслоения волокон E → M.

Кривизна связности Эресмана также удовлетворяет версии тождества Бьянки :

${\displaystyle \left[\varPhi ,R\right]=0}$

где снова [-,-] — скобка Фрёлихера-Нийенхейса для Φ ∈ Ω ¹ ( E , TE ) и R ∈ Ω ² ( E , TE ).

Полнота

Связность Эресмана позволяет кривым иметь уникальные горизонтальные подъемы локально . Для полной связности Эресмана кривая может быть горизонтально поднята над всей своей областью определения.

Холономия

Плоскость связности локально соответствует интегрируемости Фробениуса горизонтальных пространств. На другом полюсе неисчезающая кривизна подразумевает наличие голономии связности. ^[4]

Особые случаи

Главные пучки и главные соединения

Форму связности главного расслоения можно рассматривать как оператор проекции на касательное расслоение главного расслоения . Ядро формы связности задается горизонтальными подпространствами для соответствующей связности Эресмана. ${\displaystyle \omega }$ ${\displaystyle TP}$ ${\displaystyle P}$

Предположим, что E — гладкое главное G -расслоение над M. Тогда связность Эресмана H на E называется главной (Эресмановой) связностью ^[3], если она инвариантна относительно действия G на E в том смысле, что

${\displaystyle H_{eg}=\mathrm {d} (R_{g})_{e}(H_{e})}$для любых e ∈ E и g ∈ G ; здесь обозначает дифференциал правого действия g на E в точке e . ${\displaystyle \mathrm {d} (R_{g})_{e}}$

Однопараметрические подгруппы G действуют вертикально на E. Дифференциал этого действия позволяет отождествить подпространство с алгеброй Ли g группы G , скажем, с помощью отображения . Форму связности Φ связности Эресмана можно тогда рассматривать как 1-форму ω на E со значениями в g , определяемыми соотношением ω ( X )= ι ( Φ ( X )). ${\displaystyle V_{e}}$ ${\displaystyle \iota \colon V_{e}\to {\mathfrak {g}}}$

Таким образом, переосмысленная форма связи ω удовлетворяет следующим двум свойствам:

• Он преобразуется эквивариантно относительно действия G : для всех h ∈ G , где R h _* ^— обратный образ относительно правого действия, а Ad — присоединенное представление G на ее алгебре Ли. ${\displaystyle R_{h}^{*}\omega ={\hbox{Ad}}(h^{-1})\omega }$
• Он отображает вертикальные векторные поля в связанные с ними элементы алгебры Ли: ω ( X )= ι ( X ) для всех X ∈ V .

Наоборот, можно показать, что такая g -значная 1-форма на главном расслоении порождает горизонтальное распределение, удовлетворяющее вышеупомянутым свойствам.

При наличии локальной тривиализации можно свести ω к горизонтальным векторным полям (в этой тривиализации). Это определяет 1-форму ω' на M посредством пулбэка . Форма ω' полностью определяет ω , но она зависит от выбора тривиализации. (Эта форма часто также называется формой связи и обозначается просто ω .)

Векторные расслоения и ковариантные производные

Предположим, что E — гладкое векторное расслоение над M. Тогда связность Эресмана H на E называется линейной (связностью Эресмана) , если H _e линейно зависит от e ∈ E _x для каждого x ∈ M. Для уточнения пусть S _λ обозначает скалярное умножение на λ на E. Тогда H является линейной тогда и только тогда, когда для любого e ∈ E и скаляра λ. ${\displaystyle H_{\lambda e}=\mathrm {d} (S_{\lambda })_{e}(H_{e})}$

Так как E является векторным расслоением, его вертикальное расслоение V изоморфно π * E . Следовательно, если s является сечением E , то Φ (d s ): TM → s * V = s * π * E = E . Это морфизм векторного расслоения, и поэтому он задается сечением ∇ s векторного расслоения Hom( TM , E ). Тот факт, что связность Эресмана линейна, подразумевает, что, кроме того, она выполняется для каждой функции по правилу Лейбница, т. е . , и, следовательно, является ковариантной производной s . ${\displaystyle f}$ ${\displaystyle M}$ ${\displaystyle \nabla (fs)=f\nabla (s)+d(f)\otimes s}$

Наоборот, ковариантная производная ∇ на векторном расслоении определяет линейную связность Эресмана, определяя H _e для e ∈ E с x = π ( e ) как образ d s _x ( T _x M ), где s — сечение E с s ( x ) = e и ∇ _X s = 0 для всех X ∈ T _x M .

Обратите внимание, что (по историческим причинам) термин «линейный» применительно к связям иногда используется (как и слово «аффинный»  — см. Аффинное соединение ) для обозначения связностей, определенных на касательном расслоении или расслоении фрейма .

Ассоциированные пакеты

Связность Эресмана на расслоении волокон (снабженном структурной группой) иногда порождает связность Эресмана на ассоциированном расслоении . Например, (линейная) связность в векторном расслоении E , рассматриваемая как дающая параллельность E , как указано выше, индуцирует связность на ассоциированном расслоении фреймов P E расслоения E . Наоборот, связность в P E порождает (линейную) связность в E при условии, что связность в P E является эквивариантной относительно действия общей линейной группы на фреймах (и, таким образом, главной связностью ). Связность Эресмана не всегда может естественным образом индуцировать связность на ассоциированном расслоении. Например, неэквивариантная связность Эресмана на расслоении фреймов векторного расслоения может не индуцировать связность на векторном расслоении.

Предположим, что E — ассоциированное расслоение P , так что E = P × _G F. G - связность на E — это связность Эресмана, такая что отображение параллельного переноса τ : F _x → F _x′ задается G -преобразованием волокон (над достаточно близкими точками x и x ′ в M, соединенными кривой). ^[5]

Если задана главная связность на P , то с помощью обратного протягивания можно получить G -связность на соответствующем расслоении E = P × _G F .

Наоборот, если задана G -связность на E, то можно восстановить главную связность на ассоциированном главном расслоении P . Чтобы восстановить эту главную связность, вводится понятие фрейма на типичном слое F . Поскольку G является конечномерной ^[6] группой Ли, действующей эффективно на F , должна существовать конечная конфигурация точек ( y ₁ ,..., y _m ) внутри F такая, что G -орбита R = {( gy ₁ ,..., gy _m ) | g ∈ G } является главным однородным пространством G . Можно думать, что R дает обобщение понятия фрейма для G -действия на F . Заметим, что, поскольку R является главным однородным пространством для G , расслоение E ( R ), ассоциированное с E с типичным слоем R, является (эквивалентным) главному расслоению, ассоциированному с E . Но оно также является подрасслоением m -кратного произведения расслоения E с самим собой. Распределение горизонтальных пространств на E индуцирует распределение пространств на этом расслоении произведений. Поскольку параллельные транспортные отображения, связанные с соединением, являются G -отображениями, они сохраняют подпространство E ( R ), и поэтому G -связность спускается до главной G -связности на E ( R ).

Подводя итог, можно сказать, что существует взаимно-однозначное соответствие (с точностью до эквивалентности) между спусками главных соединений в ассоциированные расслоения волокон и G -связями на ассоциированных расслоениях волокон. По этой причине в категории расслоений волокон со структурной группой G главное соединение содержит всю необходимую информацию для G -связей на ассоциированных расслоениях. Следовательно, если нет настоятельных причин рассматривать соединения на ассоциированных расслоениях (как, например, в случае соединений Картана ), обычно работают напрямую с главным соединением.

Примечания

1. Эти соображения в равной степени применимы к более общей ситуации, в которой есть сюръективная субмерсия : т. е. E — расслоенное многообразие над M. В альтернативном обобщении, предложенном Лэнгом (1999) и Элиасоном (1967), E и M могут быть банаховыми многообразиями , причем E — расслоенное волокно над M, как указано выше. ${\displaystyle \pi \colon E\to M}$
2. Коларж, Михор и Словак (1993), стр.  ^{[ нужна страница ]} .
3. Кобаяши и Номидзу (1996a), стр.  ^{[ нужна страница ]} , Vol. 1.
4. Голономия для связностей Эресмана в расслоениях иногда называется голономией Эресмана-Риба или листовой голономией в связи с первым подробным исследованием с использованием связностей Эресмана для изучения слоений в (Reeb 1952)
5. См. также Lumiste (2001b), «Связи на многообразии».
6. Для удобства мы предполагаем, что G конечномерен, хотя это предположение можно смело отбросить, внеся небольшие изменения.

Ссылки

• Эресманн, Шарль (1950), Les connexions infinitésimales dans un espace fibré différentiable (PDF) , Colloque de Topologie, Брюссель, Жорж Тон, Льеж; Masson & cie, Париж, стр. 29–55.
• Эресманн, Чарльз (1952), Les connexions infinitésimales dans un espace fibré différentiable (PDF) , Séminaire N. Bourbaki, vol. 24, стр. 153–168.
• Элиасон, Х. (1967), «Геометрия многообразий отображений», Журнал дифференциальной геометрии , 1 : 169–194
• Кобаяси, Сёсичи (1957), «Теория связей», Ann. Mat. Pura Appl. , 43 : 119–194, doi : 10.1007/BF02411907 , MR  0096276, S2CID  120972987
• Кобаяси, Сёсичи ; Номидзу, Кацуми (1996a), Основы дифференциальной геометрии , т. 1 (новое издание), Wiley-Interscience, ISBN 0-471-15733-3
• Кобаяси, Сёсичи ; Номидзу, Кацуми (1996b), Основы дифференциальной геометрии , т. 2 (новое издание), Wiley-Interscience, ISBN 978-0-471-15732-8
• Коларж, Иван; Михор, Петер; Словак, Ян (1993), Естественные операторы в дифференциальной геометрии (PDF) , Springer-Verlag, архивировано из оригинала (PDF) 2017-03-30 , извлечено 2007-04-25
• Ланг, Серж (1999), Основы дифференциальной геометрии , Springer-Verlag, ISBN 0-387-98593-X
• Лумисте, Юло (2001a) [1994], "Связь на расслоенном пространстве", Энциклопедия математики , EMS Press
• Лумисте, Юло (2001b) [1994], «Связи на многообразии», Энциклопедия математики , EMS Press
• Риб, Жорж (1952), Sur somees proprietés topologiques des variétés feuilletées , Париж: Герман

Дальнейшее чтение

• Рауль Ботт (1970) «Топологическое препятствие к интегрируемости», Proc. Symp. Pure Math. , 16 Amer. Math. Soc., Providence, RI.
• Кубарский, Ян; Прадинес, Жан; Рыбицкий, Томаш; Волак, Роберт, ред. (2007). Геометрия и топология многообразий: математическое наследие Чарльза Эресмана по случаю столетия со дня его рождения. Издательства Центра Банаха. Том 76. Варшава: Польская академия наук . MR  2284825.