Сжимаемый поток (или газодинамика ) — это раздел механики жидкости , который имеет дело с потоками, имеющими значительные изменения плотности жидкости . Хотя все потоки являются сжимаемыми , потоки обычно рассматриваются как несжимаемые , когда число Маха (отношение скорости потока к скорости звука) меньше 0,3 (поскольку изменение плотности из-за скорости в этом случае составляет около 5%). [1] Изучение сжимаемого потока актуально для высокоскоростных самолетов, реактивных двигателей, ракетных двигателей, высокоскоростного входа в планетарную атмосферу, газопроводов, коммерческих приложений, таких как абразивоструйная обработка, и многих других областей.
Изучение газовой динамики часто ассоциируется с полетом современных высокоскоростных самолетов и возвращением в атмосферу космических исследовательских аппаратов; однако его истоки лежат в более простых машинах. В начале 19-го века исследование поведения выпущенных пуль привело к улучшению точности и возможностей орудий и артиллерии. [2] В течение столетия изобретатели, такие как Густав де Лаваль, продвигали эту область, в то время как исследователи, такие как Эрнст Мах, стремились понять физические явления, связанные с этим, посредством экспериментов.
В начале 20-го века фокус исследований газовой динамики сместился в сторону того, что в конечном итоге стало аэрокосмической промышленностью. Людвиг Прандтль и его ученики предложили важные концепции, начиная от пограничного слоя до сверхзвуковых ударных волн , сверхзвуковых аэродинамических труб и конструкции сверхзвукового сопла. [2] Теодор фон Карман , ученик Прандтля, продолжил улучшать понимание сверхзвукового потока. Другие известные фигуры ( Мейер , Луиджи Крокко и Ашер Шапиро ) также внесли значительный вклад в принципы, считающиеся основополагающими для изучения современной газовой динамики. Многие другие также внесли свой вклад в эту область.
Сопровождая улучшение концептуального понимания газовой динамики в начале 20-го века, общественное заблуждение, что существует барьер для достижимой скорости самолета, обычно называемый « звуковым барьером ». По правде говоря, барьер для сверхзвукового полета был просто технологическим, хотя это был упорный барьер для преодоления. Среди других факторов, обычные аэродинамические профили показали резкое увеличение коэффициента сопротивления, когда поток приближался к скорости звука. Преодоление большего сопротивления оказалось сложным для современных конструкций, отсюда и восприятие звукового барьера. Тем не менее, проектирование самолетов достаточно продвинулось, чтобы создать Bell X-1 . Пилотируемый Чаком Йегером , X-1 официально достиг сверхзвуковой скорости в октябре 1947 года. [3]
Исторически для дальнейшего углубления знаний в области газовой динамики использовались два параллельных пути исследований. Экспериментальная газовая динамика проводит эксперименты в аэродинамических моделях, а также эксперименты в ударных трубах и баллистических полигонах с использованием оптических методов для документирования результатов. Теоретическая газовая динамика рассматривает уравнения движения, применяемые к газу переменной плотности, и их решения. Большая часть базовой газовой динамики является аналитической, но в современную эпоху вычислительная гидродинамика использует вычислительную мощность для решения в противном случае неразрешимых нелинейных уравнений в частных производных сжимаемого потока для определенных геометрий и характеристик потока.

В базовой теории сжимаемого потока есть несколько важных предположений. Все жидкости состоят из молекул, но отслеживание огромного количества отдельных молекул в потоке (например, при атмосферном давлении) не является необходимым. Вместо этого предположение о континууме позволяет нам рассматривать текущий газ как непрерывную субстанцию, за исключением случаев низкой плотности. Это предположение обеспечивает огромное упрощение, которое является точным для большинства газодинамических задач. Только в области низкой плотности динамики разреженного газа движение отдельных молекул становится важным.
Связанное предположение — условие отсутствия скольжения , при котором скорость потока на твердой поверхности предполагается равной скорости самой поверхности, что является прямым следствием предположения о непрерывном течении. Условие отсутствия скольжения подразумевает, что поток является вязким, и в результате на телах, движущихся по воздуху с высокой скоростью, образуется пограничный слой , во многом как в случае низкоскоростного течения.
Большинство задач в несжимаемом потоке включают только два неизвестных: давление и скорость, которые обычно находятся путем решения двух уравнений, описывающих сохранение массы и линейного импульса, при этом плотность жидкости предполагается постоянной. Однако в сжимаемом потоке плотность газа и температура также становятся переменными. Это требует еще двух уравнений для решения задач сжимаемого потока: уравнения состояния для газа и уравнения сохранения энергии . Для большинства газодинамических задач простым уравнением состояния является закон идеального газа . В противном случае необходимо рассмотреть более сложные уравнения состояния и установить так называемую динамику неидеальной сжимаемой жидкости (NICFD).
Задачи динамики жидкости имеют два общих типа систем отсчета, называемые Лагранжевыми и Эйлеровыми (см. Жозеф-Луи Лагранж и Леонард Эйлер ). Лагранжев подход следует за массой жидкости фиксированной идентичности, когда она движется через поле потока. Эйлерова система отсчета, напротив, не движется вместе с жидкостью. Скорее, это фиксированная система или контрольный объем, через который течет жидкость. Эйлерова система отсчета наиболее полезна в большинстве задач сжимаемого потока, но требует, чтобы уравнения движения были записаны в совместимом формате.
Наконец, хотя известно, что пространство имеет 3 измерения, можно получить важное упрощение в математическом описании газовой динамики, если только одно пространственное измерение имеет первостепенное значение, поэтому предполагается одномерный поток. Это хорошо работает в потоках в каналах, соплах и диффузорах, где свойства потока изменяются в основном в направлении потока, а не перпендикулярно потоку. Однако важный класс сжимаемых потоков, включая внешний поток над телами, движущимися с высокой скоростью, требует как минимум двумерного рассмотрения. Когда важны все 3 пространственных измерения и, возможно, также временное измерение, мы часто прибегаем к компьютерным решениям основных уравнений.
Число Маха (M) определяется как отношение скорости объекта (или потока) к скорости звука. Например, в воздухе при комнатной температуре скорость звука составляет около 340 м/с (1100 футов/с). M может находиться в диапазоне от 0 до ∞, но этот широкий диапазон естественным образом попадает в несколько режимов течения. Эти режимы — дозвуковой, трансзвуковой , сверхзвуковой , гиперзвуковой и гиперскоростной поток. На рисунке ниже показан «спектр» чисел Маха этих режимов течения.
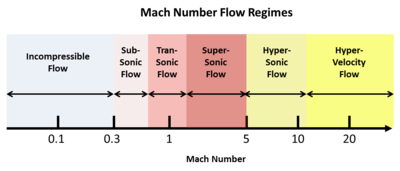
Эти режимы течения не выбираются произвольно, а скорее возникают естественным образом из сильного математического фона, лежащего в основе сжимаемого течения (см. цитируемые справочные учебники). При очень низких скоростях течения скорость звука настолько выше, что математически игнорируется, а число Маха не имеет значения. Однако, как только скорость течения приближается к скорости звука, число Маха становится важнейшим, и начинают появляться ударные волны. Таким образом, трансзвуковой режим описывается другой (и гораздо более сложной) математической трактовкой. В сверхзвуковом режиме течение определяется волновым движением под косыми углами, подобными углу Маха. Выше примерно 5 Маха эти волновые углы становятся настолько малыми, что требуется другой математический подход, определяющий режим гиперзвуковой скорости . Наконец, при скоростях, сопоставимых со скоростью входа в атмосферу планеты с орбиты, в диапазоне нескольких км/с, скорость звука теперь сравнительно настолько мала, что она снова математически игнорируется в режиме гиперскорости .
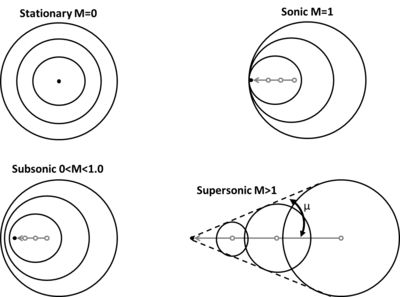
Когда объект ускоряется от дозвуковой до сверхзвуковой скорости в газе, происходят различные типы волновых явлений. Для иллюстрации этих изменений на следующем рисунке показана неподвижная точка (M = 0), которая испускает симметричные звуковые волны. Скорость звука одинакова во всех направлениях в однородной жидкости, поэтому эти волны представляют собой просто концентрические сферы. Когда точка, генерирующая звук, начинает ускоряться, звуковые волны «сгущаются» в направлении движения и «растягиваются» в противоположном направлении. Когда точка достигает звуковой скорости (M = 1), она движется с той же скоростью, что и создаваемые ею звуковые волны. Поэтому бесконечное количество этих звуковых волн «накапливается» впереди точки, образуя ударную волну . Достигнув сверхзвукового потока, частица движется так быстро, что она непрерывно оставляет свои звуковые волны позади. Когда это происходит, геометрическое место этих волн, тянущихся за точкой, создает угол, известный как угол волны Маха или угол Маха, μ:
где представляет собой скорость звука в газе, а представляет собой скорость объекта. Хотя эти косые волны названы в честь австрийского физика Эрнста Маха , их впервые обнаружил Кристиан Доплер . [4]
Одномерный (1-D) поток относится к потоку газа через воздуховод или канал, в котором предполагается, что параметры потока существенно изменяются только вдоль одного пространственного измерения, а именно, длины воздуховода. При анализе потока в 1-D канале делается ряд предположений:
По мере того, как скорость потока увеличивается от дозвукового до сверхзвукового режима, физика потоков в сопле и диффузоре изменяется. Используя законы сохранения динамики жидкости и термодинамики, для потока в канале разработано следующее соотношение (совместное сохранение массы и импульса):
где dP — дифференциальное изменение давления, M — число Маха, ρ — плотность газа, V — скорость потока, A — площадь канала, а dA — изменение площади канала. Это уравнение утверждает, что для дозвукового потока сходящийся канал (dA < 0) увеличивает скорость потока, а расходящийся канал (dA > 0) уменьшает скорость потока. Для сверхзвукового потока происходит обратное из-за смены знака (1 − M 2 ). Сужающийся канал (dA < 0) теперь уменьшает скорость потока, а расходящийся канал (dA > 0) увеличивает скорость потока. При числе Маха = 1 возникает особый случай, в котором площадь канала должна быть либо максимальной, либо минимальной. Для практических целей только минимальная площадь может ускорить потоки до числа Маха 1 и выше. См. таблицу субсверхзвуковых диффузоров и сопел.
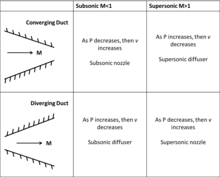
Поэтому, чтобы разогнать поток до 1 Маха, сопло должно быть спроектировано так, чтобы сходиться к минимальной площади поперечного сечения, а затем расширяться. Этот тип сопла — сходящееся-расходящееся сопло — называется соплом Лаваля в честь Густава де Лаваля , который его изобрел. Когда дозвуковой поток входит в сходящийся канал и площадь уменьшается, поток ускоряется. Достигнув минимальной площади канала, также известной как горловина сопла, поток может достичь 1 Маха. Если скорость потока должна продолжать увеличиваться, его плотность должна уменьшаться, чтобы подчиняться закону сохранения массы. Чтобы достичь этого уменьшения плотности, поток должен расширяться, и для этого поток должен проходить через расходящийся канал. Смотрите изображение сопла Лаваля.

В конечном счете, из-за закона сохранения энергии, газ ограничен определенной максимальной скоростью, основанной на его энергетическом содержании. Максимальная скорость, V max , которую может достичь газ, равна:
где c p — удельная теплоёмкость газа, T t — температура торможения потока.
Используя законы сохранения и термодинамику, ряд соотношений вида
можно получить, где M — число Маха, а γ — отношение удельных адиабат (1,4 для воздуха). См. таблицу соотношений числа Маха изоэнтропического потока.
Как упоминалось ранее, для того, чтобы поток стал сверхзвуковым, он должен пройти через канал с минимальной площадью или звуковое горло. Кроме того, для достижения числа Маха 1 необходимо общее отношение давлений P b /P t примерно 2. Как только число Маха 1, поток в горле считается задушенным . Поскольку изменения ниже по потоку могут происходить только вверх по потоку со звуковой скоростью, массовый поток через сопло не может быть затронут изменениями в условиях ниже по потоку после того, как поток задушен.
Нормальные ударные волны — это ударные волны, перпендикулярные локальному направлению потока. Эти ударные волны возникают, когда волны давления накапливаются и сливаются в чрезвычайно тонкую ударную волну, которая преобразует кинетическую энергию в тепловую . Таким образом, волны догоняют и усиливают друг друга, образуя конечную ударную волну из бесконечной серии бесконечно малых звуковых волн. Поскольку изменение состояния через ударную волну в высшей степени необратимо, энтропия увеличивается через ударную волну. При анализе нормальной ударной волны предполагается одномерный, стационарный и адиабатический поток идеального газа. Температура торможения и энтальпия торможения одинаковы вверх и вниз по потоку от ударной волны.
Нормальные ударные волны можно легко проанализировать в любой из двух систем отсчета: стоячей нормальной ударной волне и движущейся ударной волне. Поток перед нормальной ударной волной должен быть сверхзвуковым, а поток после нормальной ударной волны должен быть дозвуковым. Уравнения Ренкина-Гюгонио используются для решения условий потока.
Хотя одномерный поток может быть проанализирован напрямую, это всего лишь частный случай двумерного потока. Из этого следует, что одно из определяющих явлений одномерного потока, прямой скачок уплотнения, также является лишь частным случаем более крупного класса косых скачков уплотнения . Кроме того, название «нормальный» относится к геометрии, а не к частоте возникновения. Косые скачки уплотнения гораздо более распространены в таких приложениях, как: конструкция воздухозаборника самолета, объекты в сверхзвуковом полете и (на более фундаментальном уровне) сверхзвуковые сопла и диффузоры. В зависимости от условий потока косой скачок уплотнения может быть либо присоединен к потоку, либо отделен от потока в виде головной ударной волны .
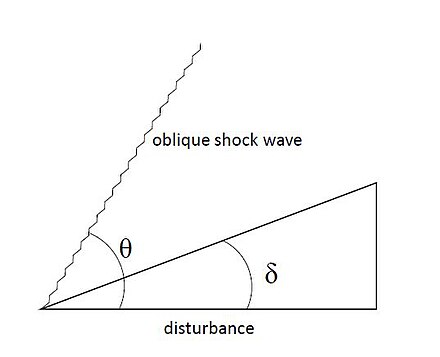
Косые ударные волны похожи на нормальные ударные волны, но они возникают под углами менее 90° с направлением потока. Когда в поток вносится возмущение под ненулевым углом (δ), поток должен реагировать на изменяющиеся граничные условия. Таким образом, образуется косой скачок уплотнения, что приводит к изменению направления потока.

На основе уровня отклонения потока (δ) косые скачки уплотнения характеризуются как сильные или слабые. Сильные скачки уплотнения характеризуются большим отклонением и большей потерей энтропии через скачок уплотнения, а слабые скачки уплотнения — наоборот. Чтобы получить беглое представление о различиях в этих скачках, можно использовать полярную диаграмму скачков уплотнения. При известной статической температуре после скачка уплотнения, T*, скорость звука после скачка уплотнения определяется как,
где R — газовая постоянная, а γ — удельное отношение теплоемкости. Число Маха можно разбить на декартовы координаты
где V x и V y — x- и y-компоненты скорости жидкости V. При заданном числе Маха перед скачком уплотнения можно задать геометрическое место условий. При некотором δ max поток переходит от сильного к слабому косому скачку уплотнения. При δ = 0° на границе сильного косого скачка уплотнения образуется прямой скачок уплотнения, а на границе слабого скачка уплотнения образуется волна Маха.
Из-за наклона скачка уплотнения, после создания косого скачка уплотнения, он может взаимодействовать с границей тремя различными способами, два из которых описаны ниже.
Входящий поток сначала поворачивается на угол δ по отношению к потоку. Эта ударная волна отражается от твердой границы, и поток поворачивается на – δ, чтобы снова стать параллельным границе. Каждая прогрессивная ударная волна слабее, а угол волны увеличивается.
Нерегулярное отражение очень похоже на случай, описанный выше, с той оговоркой, что δ больше максимально допустимого угла поворота. Таким образом, образуется оторванный скачок и происходит более сложное отражение, известное как отражение Маха.
Веера Прандтля–Майера могут быть выражены как веера сжатия и расширения. Веера Прандтля–Майера также пересекают пограничный слой (т. е. текущий и твердый), который также реагирует различными изменениями. Когда ударная волна ударяется о твердую поверхность, полученный веер возвращается как веер из противоположного семейства, а когда ударяется о свободную границу, веер возвращается как веер противоположного типа.

До сих пор единственными явлениями течения, которые обсуждались, были ударные волны, которые замедляют поток и увеличивают его энтропию. Можно ускорить сверхзвуковой поток в том, что было названо веером расширения Прандтля–Майера , в честь Людвига Прандтля и Теодора Майера. Механизм расширения показан на рисунке ниже.
В отличие от потока, встречающего наклонное препятствие и образующего косой скачок уплотнения, поток расширяется вокруг выпуклого угла и образует веер расширения через серию изэнтропических волн Маха. «Веер» расширения состоит из волн Маха, которые охватывают от начального угла Маха до конечного угла Маха. Поток может расширяться как вокруг острого, так и вокруг закругленного угла в равной степени, поскольку увеличение числа Маха пропорционально только выпуклому углу прохода (δ). Угол расширения, который создает веер Прандтля–Майера, может быть острым (как показано на рисунке) или закругленным. Если общий угол поворота одинаков, то решение для потока PM также одинаково.
Расширение Прандтля–Майера можно рассматривать как физическое объяснение работы сопла Лаваля. Контур сопла создает плавную и непрерывную серию волн расширения Прандтля–Майера.

Сжатие Прандтля–Майера — явление, противоположное расширению Прандтля–Майера. Если поток постепенно поворачивать на угол δ, может образоваться веер сжатия. Этот веер представляет собой серию волн Маха, которые в конечном итоге сливаются в косой скачок уплотнения. Поскольку поток определяется изоэнтропической областью (поток, проходящий через веер) и анизоэнтропической областью (поток, проходящий через косой скачок уплотнения), между двумя областями течения возникает линия скольжения.
Сверхзвуковые аэродинамические трубы используются для испытаний и исследований в сверхзвуковых потоках, примерно в диапазоне чисел Маха от 1,2 до 5. Принцип работы аэродинамической трубы заключается в том, что вверх и вниз по потоку поддерживается большая разность давлений, что приводит в движение поток.

Аэродинамические трубы можно разделить на две категории: непрерывно работающие и прерывисто работающие. Непрерывно работающие сверхзвуковые аэродинамические трубы требуют независимого источника электроэнергии, который резко увеличивается с размером испытательной секции. Прерывисто работающие сверхзвуковые аэродинамические трубы менее дороги, поскольку они хранят электрическую энергию в течение длительного периода времени, а затем разряжают ее в течение серии коротких испытаний. Разница между ними аналогична сравнению между батареей и конденсатором.
Сверхзвуковые аэродинамические трубы типа Blowdown предлагают высокое число Рейнольдса, небольшой резервуар для хранения и легкодоступный сухой воздух. Однако они создают опасность высокого давления, затрудняют поддержание постоянного давления застоя и шумят во время работы.
Сверхзвуковые аэродинамические трубы Indraft не связаны с опасностью давления, допускают постоянное давление застоя и относительно тихие. К сожалению, они имеют ограниченный диапазон для числа Рейнольдса потока и требуют большого вакуумного резервуара.
Нет никаких сомнений в том, что знания приобретаются посредством исследований и испытаний в сверхзвуковых аэродинамических трубах; однако, эти установки часто требуют огромного количества энергии для поддержания больших отношений давления, необходимых для условий испытаний. Например, Arnold Engineering Development Complex имеет самую большую сверхзвуковую аэродинамическую трубу в мире и требует для работы мощности, необходимой для освещения небольшого города. По этой причине большие аэродинамические трубы становятся все менее распространенными в университетах.
Возможно, наиболее распространенное требование к косым скачкам уплотнения — это входные отверстия сверхзвуковых самолетов для скоростей более 2 Маха (максимальная скорость F-16 составляет 2 Маха, но ему не нужен косой скачок уплотнения). Одной из целей входного отверстия является минимизация потерь через скачки уплотнения, поскольку входящий сверхзвуковой воздух замедляется до дозвуковой скорости перед тем, как попасть в турбореактивный двигатель. Это достигается с помощью одного или нескольких косых скачков уплотнения, за которыми следует очень слабый прямой скачок уплотнения, с числом Маха вверх по потоку, как правило, менее 1,4. Воздушный поток через впускное отверстие должен правильно управляться в широком диапазоне скоростей от нуля до максимальной сверхзвуковой скорости. Это делается путем изменения положения поверхностей впуска.
Хотя для достижения приемлемых характеристик от взлета до скоростей, превышающих 2 Маха, требуется переменная геометрия, не существует единого метода ее достижения. Например, для максимальной скорости около 3 Маха XB-70 использовал прямоугольные входы с регулируемыми рампами, а SR-71 использовал круглые входы с регулируемым входным конусом .