Геометрия такси

Тип метрической геометрии

В геометрии такси длины красного, синего, зеленого и желтого путей равны 12 , то есть расстоянию такси между противоположными углами, и все четыре пути являются кратчайшими. Вместо этого в евклидовой геометрии красный, синий и желтый пути по-прежнему имеют длину 12 , но зеленый путь — это уникальный кратчайший путь, длина которого равна евклидову расстоянию между противоположными углами, 6√2 ≈ 8,49 .

Геометрия такси или геометрия Манхэттена — это геометрия , в которой знакомое евклидово расстояние игнорируется, а расстояние между двумя точками вместо этого определяется как сумма абсолютных разностей их соответствующих декартовых координат , функция расстояния (или метрика ), называемая расстоянием такси . Расстояние до Манхэттена или расстояние до городского квартала . Название относится к острову Манхэттен или, в целом, к любому запланированному городу с прямоугольной сеткой улиц, в котором такси может передвигаться только по направлениям сетки. В геометрии такси расстояние между любыми двумя точками равно длине их кратчайшего пути сетки. Это другое определение расстояния также приводит к другому определению длины кривой, для которой отрезок линии между любыми двумя точками имеет ту же длину, что и путь сетки между этими точками, а не его евклидову длину.

Расстояние такси также иногда называют прямолинейным расстоянием или расстоянием L ¹ (см. пространство L p ). ^[1] Эта геометрия используется в регрессионном анализе с 18 века и часто называется LASSO . Его геометрическая интерпретация восходит к неевклидовой геометрии XIX века и принадлежит Герману Минковскому .

В двумерном пространстве реальных координат расстояние такси между двумя точками и равно . То есть это сумма абсолютных значений разностей по обеим координатам. ${\displaystyle \mathbb {R} ^{2},}$ ${\displaystyle (x_{1},y_{1})}$ ${\displaystyle (x_{2},y_{2})}$ ${\displaystyle \left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|}$

Формальное определение

Расстояние такси между двумя точками в n -мерном реальном координатном пространстве с фиксированной декартовой системой координат представляет собой сумму длин проекций отрезка прямой между точками на оси координат . Более формально, ${\displaystyle d_{\text{T}}}$ ${\displaystyle \mathbf {p} =(p_{1},p_{2},\dots ,p_{n}){\text{ and }}\mathbf {q} =(q_{1},q_{2},\dots ,q_{n})}$

$${\displaystyle d_{\text{T}}(\mathbf {p} ,\mathbf {q} )=\left\|\mathbf {p} -\mathbf {q} \right\|_{\text{T}}=\sum _{i=1}^{n}\left|p_{i}-q_{i}\right|}$$

${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \mathbf {p} =(p_{1},p_{2})}$ ${\displaystyle \mathbf {q} =(q_{1},q_{2})}$ ${\displaystyle \left|p_{1}-q_{1}\right|+\left|p_{2}-q_{2}\right|.}$

История

Метрика L ¹ была использована в регрессионном анализе как мера согласия в 1757 году Роджером Джозефом Босковичем . ^[2] Интерпретация этого понятия как расстояния между точками в геометрическом пространстве восходит к концу 19 века и развитию неевклидовой геометрии . Примечательно, что он появился в 1910 году в работах Фригеса Риса и Германа Минковского . Формализация пространств Lp , которые включают ^в себя геометрию такси как особый случай, принадлежит Риссу. ^[3] Развивая геометрию чисел , Герман Минковский установил свое неравенство Минковского , заявив, что эти пространства определяют нормированные векторные пространства . ^[4]

Название «геометрия такси» было введено Карлом Менгером в буклете 1952 года « Вам понравится геометрия» , сопровождавшем выставку геометрии, предназначенную для широкой публики в Музее науки и промышленности в Чикаго. ^[5]

Характеристики

Расстояние между такси , рассматриваемое как дополнительная структура, наслоенная на евклидово пространство , зависит от ориентации системы координат и изменяется в результате евклидова вращения пространства, но на него не влияют сдвиги или отражения , ориентированные по оси . Геометрия такси удовлетворяет всем аксиомам Гильберта (формализация евклидовой геометрии ), за исключением того, что конгруэнтность углов не может быть определена так, чтобы точно соответствовать евклидовой концепции, и при правдоподобных определениях конгруэнтных углов такси аксиома сторона-угол-сторона не выполняется как В общем случае треугольники с двумя сторонами, равными такси, и углом, равным такси, между ними не являются конгруэнтными треугольниками .

Сферы

Точки сетки на круге в геометрии такси, поскольку сетка становится более мелкой.

В любом метрическом пространстве сфера представляет собой набор точек, находящихся на фиксированном расстоянии ( радиусе ) от определенной центральной точки. В то время как евклидова сфера круглая и вращательно-симметричная, на расстоянии такси форма сферы представляет собой перекрестный многогранник , n -мерное обобщение правильного октаэдра , точки которого удовлетворяют уравнению: ${\displaystyle \mathbf {p} }$

${\displaystyle d_{\text{T}}(\mathbf {p} ,\mathbf {c} )=\sum _{i=1}^{n}|p_{i}-c_{i}|=r,}$

где – центр, а r – радиус. Точки на единичной сфере , сфере радиуса 1 с центром в начале координат , удовлетворяют уравнению ${\displaystyle \mathbf {c} }$ ${\displaystyle \mathbf {p} }$ ${\textstyle d_{\text{T}}(\mathbf {p} ,\mathbf {0} )=\sum _{i=1}^{n}|p_{i}|=1.}$

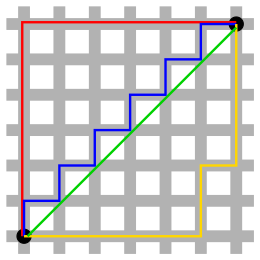
В двумерной геометрии такси сфера (называемая кругом ) представляет собой квадрат , ориентированный по диагонали к осям координат. На изображении справа красным цветом показан набор всех точек квадратной сетки с фиксированным расстоянием от синего центра. По мере того, как сетка становится более мелкой, красных точек становится больше и в пределе они стремятся к сплошному наклоненному квадрату. Таксиевая длина каждой стороны равна 2 р , поэтому длина окружности равна 8 р . Таким образом, в геометрии такси значение аналога постоянной окружности π — отношения длины окружности к диаметру — равно 4.

Замкнутый шар (или закрытый диск в двумерном случае) представляет собой заполненную сферу, совокупность точек, находящихся на расстоянии меньшем или равном радиусу от определенного центра. Для клеточных автоматов на квадратной сетке диск такси - это окрестность фон Неймана диапазона r его центра.

Окружность радиуса r для расстояния Чебышева ( метрика L ∞ ) на плоскости также представляет собой квадрат со стороной 2 r , параллельной осям координат, поэтому плоское расстояние Чебышева можно рассматривать как эквивалентное путем вращения и масштабирования плоскому расстоянию такси. Однако эта эквивалентность между метриками L ₁ и L _∞ не распространяется на более высокие измерения.

Всякий раз, когда каждая пара в наборе этих кругов имеет непустое пересечение, существует точка пересечения для всего набора; следовательно, манхэттенское расстояние образует инъективное метрическое пространство .

Длина дуги

Пусть – непрерывно дифференцируемая функция по . Пусть – длина дуги такси плоской кривой , определенной на некотором интервале . Тогда длина такси бесконечно малого регулярного разбиения дуги определяется выражением: ^[6] ${\displaystyle y=f(x)}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle s}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle i^{\text{th}}}$ ${\displaystyle \Delta s_{i}}$

${\displaystyle \Delta s_{i}=\Delta x_{i}+\Delta y_{i}=\Delta x_{i}+|f(x_{i})-f(x_{i-1})|}$

По теореме о среднем значении существует некоторая точка между и такая, что . ^[7] ${\displaystyle x_{i}^{*}}$ ${\displaystyle x_{i}}$ ${\displaystyle x_{i-1}}$ ${\displaystyle f(x_{i})-f(x_{i-1})=f'(x_{i}^{*})dx_{i}}$

${\displaystyle \Delta s_{i}=\Delta x_{i}+|f'(x_{i}^{*})|\Delta x_{i}=\Delta x_{i}(1+|f'(x_{i}^{*})|)}$

Затем задается как сумма всех разделов on, когда они становятся сколь угодно малыми . ${\displaystyle s}$ ${\displaystyle s}$ ${\displaystyle [a,b]}$

Кривые, определяемые монотонными возрастающими или убывающими функциями, имеют одинаковую длину дуги такси, если они имеют одни и те же конечные точки.

${\displaystyle {\begin{aligned}s&=\lim _{n\rightarrow \infty }\sum _{i=1}^{n}\Delta x_{i}(1+|f'(x_{i}^{*})|)\\&=\int _{a}^{b}1+|f'(x)|\,dx\end{aligned}}}$

Чтобы проверить это, возьмем круг такси с центром в начале координат. Его кривая в первом квадранте определяется длиной ${\displaystyle r}$ ${\displaystyle f(x)=-x+r}$

${\displaystyle s=\int _{0}^{r}1+|-1|dx=2r}$

Умножение этого значения на для учета оставшихся квадрантов дает , что соответствует длине окружности такси. ^[8] Теперь возьмем евклидову окружность радиуса с центром в начале координат, который определяется как . Длина его дуги в первом квадранте определяется выражением ${\displaystyle 4}$ ${\displaystyle 8r}$ ${\displaystyle r}$ ${\displaystyle f(x)={\sqrt {r^{2}-x^{2}}}}$

${\displaystyle {\begin{aligned}s&=\int _{0}^{r}1+|{\frac {-x}{\sqrt {r^{2}-x^{2}}}}|dx\\&=x+{\sqrt {r^{2}-x^{2}}}{\bigg |}_{0}^{r}\\&=r-(-r)\\&=2r\end{aligned}}}$

Учет остальных квадрантов дает снова. Следовательно, длина окружности такси и евклидова круга в метрике такси равны. ^[9] Фактически, для любой функции , которая является монотонной и дифференцируемой с непрерывной производной на интервале , длина дуги над равна . ^[10] ${\displaystyle 4\times 2r=8r}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle (b-a)+\mid f(b)-f(a)\mid }$

Конгруэнтность треугольника

Два прямоугольных равнобедренных треугольника такси. Три угла и два катета равны, а треугольники не равны. Следовательно, ASASA не является теоремой сравнения в геометрии такси.

Два треугольника равны тогда и только тогда, когда три соответствующие стороны равны по расстоянию и три соответствующих угла равны по мере. Существует несколько теорем, гарантирующих конгруэнтность треугольников в евклидовой геометрии, а именно: «Угол-Угол-Сторона» (AAS), «Угол-Сторона-Угол» (ASA), «Сторона-Угол-Сторона» (SAS) и «Сторона-Сторона-Сторона» (SSS). Однако в геометрии такси только SASAS гарантирует конгруэнтность треугольников. ^[11]

Возьмем, к примеру, два прямоугольных равнобедренных треугольника такси, углы которых составляют 45-90-45. Два катета обоих треугольников имеют длину такси 2, но гипотенузы не равны. Этот контрпример исключает AAS, ASA и SAS. Он также исключает AASS, AAAS и даже ASASA. Наличие трех равных углов и двух сторон не гарантирует совпадение треугольников в геометрии такси. Следовательно, единственной теоремой о конгруэнтности треугольников в геометрии такси является SASAS, где все три соответствующие стороны должны быть конгруэнтны и как минимум два соответствующих угла должны быть конгруэнтны. ^[12] Этот результат обусловлен главным образом тем, что длина отрезка прямой зависит от его ориентации в геометрии такси.

Приложения

Сжатое зондирование

При решении недоопределенной системы линейных уравнений член регуляризации вектора параметров выражается через норму (геометрию такси) вектора. ^[13] Этот подход появляется в системе восстановления сигнала, называемой сжатым зондированием . ${\displaystyle \ell _{1}}$

Различия частотных распределений

Геометрию такси можно использовать для оценки различий в распределениях дискретных частот. Например, при сплайсинге РНК позиционные распределения гексамеров , которые отображают вероятность появления каждого гексамера в каждом данном нуклеотиде вблизи сайта сплайсинга, можно сравнить с L1-расстоянием. Каждое распределение положений можно представить в виде вектора, где каждая запись представляет вероятность того, что гексамер начинается с определенного нуклеотида. Большое расстояние L1 между двумя векторами указывает на значительную разницу в характере распределений, тогда как небольшое расстояние указывает на схожую форму распределений. Это эквивалентно измерению площади между двумя кривыми распределения, поскольку площадь каждого сегмента представляет собой абсолютную разницу между вероятностями двух кривых в этой точке. Если суммировать все сегменты, это дает ту же меру, что и расстояние L1. ^[14]

Смотрите также

Сравнение чебышевского, евклидова и таксистного расстояний для гипотенузы треугольника 3-4-5 на шахматной доске

• Расстояние Чебышева
• Расстояние Хэмминга - количество битов, различающихся между двумя строками двоичных цифр.
• Расстояние Ли
• Ортогональная выпуклая оболочка  - минимальное надмножество, которое пересекает каждую линию, параллельную оси, в интервале.
• Лестничный парадокс - парадокс, заключающийся в том, что предел длин все более тонких «лестничных кривых» не стремится к длине диагонального отрезка, к которому стремятся кривые.

Рекомендации

1. Блэк, Пол Э. «Манхэттенская дистанция». Словарь алгоритмов и структур данных . Проверено 6 октября 2019 г.
2. Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Издательство Гарвардского университета. ISBN 9780674403406. Проверено 6 октября 2019 г.
3. Рисс, Фридьес (1910). «Untersuchungen über Systeme integrierbarer Funktionen». Mathematische Annalen (на немецком языке). 69 (4): 449–497. дои : 10.1007/BF01457637. hdl : 10338.dmlcz/128558 . S2CID  120242933.
4. Минковский, Герман (1910). Геометрия дер Зален (на немецком языке). Лейпциг и Берлин: Р. Г. Тойбнер. ЖФМ  41.0239.03. МР  0249269 . Проверено 6 октября 2019 г.
5. Менгер, Карл (1952). Вам понравится геометрия. Путеводитель для выставки геометрии Иллинойского технологического института . Чикаго: Музей науки и промышленности.
   Голландия, Луиза (1990). «Карл Менгер и геометрия такси». Журнал «Математика» . 63 (5): 326–327. дои : 10.1080/0025570x.1990.11977548.
6. Хайнбокель, Дж. Х. (2012). Введение в исчисление, том II . Университет Олд Доминион. стр. 54–55.
7. Пено, JP (1 января 1988 г.). «О теореме о среднем значении». Оптимизация . 19 (2): 147–156. дои : 10.1080/02331938808843330. ISSN  0233-1934.
8. Петрович, Майя; Малешевич, Бранко; Баньяк, Боян; Обрадович, Ратко (2014). Геометрия некоторых кривых такси . 4-я Международная научная конференция по геометрии и графике. Сербское общество геометрии и графики, Нишский университет, Сербия. arXiv : 1405.7579 .
9. Кемп, Обри (2018). Обобщение и перенос математических определений из евклидовой геометрии в таксомоторную геометрию (кандидатская диссертация). Государственный университет Джорджии. дои : 10.57709/12521263 .
10. Томпсон, Кевин П. (2011). «Природа длины, площади и объема в геометрии такси». Международный электронный журнал геометрии . 4 (2): 193–207. arXiv : 1101.2922 .
11. Миронычев, Александр (2018). «Условия SAS и SSA для равных треугольников». Журнал математики и системных наук . 8 (2): 59–66.
12. ТОМПСОН, КЕВИН; ДРЕЙ, ТЕВИАН (2000). «Углы такси и тригонометрия». Журнал Пи Му Эпсилон . 11 (2): 87–96. ISSN  0031-952X. JSTOR  24340535.
13. Донохо, Дэвид Л. (23 марта 2006 г.). «Для большинства больших недоопределенных систем линейных уравнений решение с минимальной нормой также является самым редким решением». Сообщения по чистой и прикладной математике . 59 (6): 797–829. дои : 10.1002/cpa.20132. S2CID  8510060. ${\displaystyle \ell _{1}}$
14. Лим, Киан Хуат; Феррарис, Лусиана; Филлу, Мадлен Э.; Рафаэль, Бенджамин Дж.; Фэйрбратер, Уильям Г. (5 июля 2011 г.). «Использование позиционного распределения для идентификации элементов сплайсинга и прогнозирования дефектов обработки пре-мРНК в генах человека». Труды Национальной академии наук Соединенных Штатов Америки . 108 (27): 11093–11098. Бибкод : 2011PNAS..10811093H. дои : 10.1073/pnas.1101135108 . ПМК 3131313 . ПМИД  21685335. 

дальнейшее чтение

• Гарднер, Мартин (1997). «10. Геометрия такси». Последние развлечения . Коперник. стр. 159–176. ISBN 0-387-94929-1.
• Краузе, Юджин Ф. (1975). Геометрия такси . Аддисон-Уэсли. ISBN 0201039346.Перепечатано Dover (1986), ISBN 0-486-25202-7 . 

Внешние ссылки

• Вайсштейн, Эрик В. «Метрика такси». Математический мир .
• Малкевич, Джо (1 октября 2007 г.). "Такси!". Американское математическое общество . Проверено 6 октября 2019 г.