Орбитальные элементы

Параметры, которые однозначно идентифицируют конкретную орбиту

Элементы орбиты — это параметры , необходимые для однозначной идентификации конкретной орбиты . В небесной механике эти элементы рассматриваются в системах двух тел с использованием орбиты Кеплера . Существует много разных способов математического описания одной и той же орбиты, но в астрономии и орбитальной механике обычно используются определенные схемы, каждая из которых состоит из набора из шести параметров .

Реальная орбита и ее элементы изменяются со временем из-за гравитационных возмущений со стороны других объектов и эффектов общей теории относительности . Орбита Кеплера — это идеализированная математическая аппроксимация орбиты в определенный момент времени.

Кеплеровы элементы

На этой диаграмме плоскость орбиты (желтая) пересекает опорную плоскость (серую). Для спутников на околоземной орбите базовой плоскостью обычно является экваториальная плоскость Земли, а для спутников на солнечных орбитах — плоскость эклиптики . Пересечение называется линией узлов , так как оно соединяет центр масс с восходящим и нисходящим узлами. Плоскость отсчета вместе с весенней точкой ( ♈︎ ) образует систему отсчета.

Традиционными орбитальными элементами являются шесть элементов Кеплера , в честь Иоганна Кеплера и его законов движения планет .

Если смотреть в инерциальной системе отсчета , два вращающихся тела следуют по разным траекториям. Каждая из этих траекторий имеет фокус в общем центре масс . Если смотреть из неинерциальной системы отсчета с центром на одном из тел, видна только траектория противоположного тела; Кеплеровы элементы описывают эти неинерциальные траектории. Орбита имеет два набора кеплеровских элементов в зависимости от того, какое тело используется в качестве точки отсчета. Тело отсчета (обычно самое массивное) называется первичным , другое тело — вторичным . Первичная звезда не обязательно обладает большей массой, чем вторичная, и даже когда тела имеют одинаковую массу, элементы орбиты зависят от выбора первичной звезды.

Два элемента определяют форму и размер эллипса:

• Эксцентриситет ( e ) — форма эллипса, описывающая, насколько он вытянут по сравнению с кругом (не отмечен на схеме).
• Большая полуось ( а ) — сумма расстояний перицентра и апоцентра, деленная на два. Для классических орбит двух тел большая полуось — это расстояние между центрами тел, а не расстояние тел от центра масс.

Два элемента определяют ориентацию орбитальной плоскости , в которую встроен эллипс:

• Наклонение ( i ) — вертикальный наклон эллипса относительно базовой плоскости, измеренный в восходящем узле (где орбита проходит вверх через опорную плоскость, зеленый угол i на диаграмме). Угол наклона измеряется перпендикулярно линии пересечения орбитальной плоскости и опорной плоскости. Любые три различные точки на эллипсе будут определять плоскость орбиты эллипса. Плоскость и эллипс являются двумерными объектами, определенными в трехмерном пространстве.
• Долгота восходящего узла ( Ω ) — горизонтально ориентирует восходящий узел эллипса (где орбита проходит с юга на север через опорную плоскость, обозначенную ☊ ) относительно весенней точки системы отсчета (обозначенной ♈︎). Это значение измеряется в базовой плоскости и показано на диаграмме зеленым углом Ω .

Остальные два элемента следующие:

• Аргумент периапсиса ( ω ) определяет ориентацию эллипса в плоскости орбиты как угол, измеренный от восходящего узла до периапсиса (ближайшая точка, в которой объект-спутник подходит к основному объекту, вокруг которого он вращается), фиолетовый угол ω на диаграмме.
• Истинная аномалия ( ν , θ или f ) в эпоху ( t ₀ ) определяет положение вращающегося тела вдоль эллипса в определенное время («эпоха»).

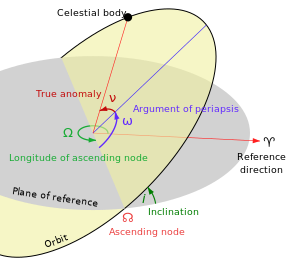
Средняя аномалия M представляет собой математически удобный воображаемый «угол», который линейно меняется со временем, но не соответствует реальному геометрическому углу. Его можно преобразовать в истинную аномалию ν , которая представляет собой реальный геометрический угол в плоскости эллипса между периапсисом (наибольшим приближением к центральному телу) и положением вращающегося объекта в любой момент времени. Таким образом, истинная аномалия показана на диаграмме красным углом ν , а средняя аномалия не показана.

Углы наклона, долгота восходящего узла и аргумент периапсиса также можно описать как углы Эйлера , определяющие ориентацию орбиты относительно базовой системы координат.

Обратите внимание, что неэллиптические траектории также существуют, но не являются замкнутыми и, следовательно, не являются орбитами. Если эксцентриситет больше единицы, траектория представляет собой гиперболу . Если эксцентриситет равен единице, а угловой момент равен нулю, траектория радиальная . Если эксцентриситет равен единице и имеется угловой момент, то траектория представляет собой параболу .

Обязательные параметры

Учитывая инерциальную систему отсчета и произвольную эпоху (заданный момент времени), необходимо ровно шесть параметров, чтобы однозначно определить произвольную и невозмущенную орбиту.

Это потому, что задача содержит шесть степеней свободы . Они соответствуют трем пространственным измерениям , которые определяют положение ( x , y , z в декартовой системе координат ), а также скорость в каждом из этих измерений. Их можно описать как векторы состояния орбиты , но часто это неудобный способ представления орбиты, поэтому вместо них обычно используются кеплеровы элементы.

Иногда эпоху считают «седьмым» параметром орбиты, а не частью системы отсчета.

Если эпоха определена как момент, когда один из элементов равен нулю, количество неуказанных элементов уменьшается до пяти. (Шестой параметр по-прежнему необходим для определения орбиты; он просто численно устанавливается равным нулю по соглашению или «перемещается» в определение эпохи относительно реального времени часов.)

Альтернативные параметризации

Кеплеровы элементы могут быть получены из векторов орбитального состояния (трехмерный вектор положения и другой вектор скорости) путем ручных преобразований или с помощью компьютерного программного обеспечения. ^[1]

Другие параметры орбиты можно вычислить из кеплеровских элементов, таких как период , апоапсис и периапсис . (При вращении вокруг Земли последние два члена известны как апогей и перигей.) В наборах кеплеровских элементов обычно указывают период вместо большой полуоси, поскольку каждый из них может быть вычислен из другого при условии стандартных гравитационных параметр GM задан для центрального тела .

Вместо средней аномалии в эпоху можно использовать среднюю аномалию M , среднюю долготу , истинную аномалию ν ₀ или (редко) эксцентрическую аномалию .

Использование, например, «средней аномалии» вместо «средней аномалии в эпоху» означает, что время t должно быть указано как седьмой орбитальный элемент. Иногда предполагается, что средняя аномалия равна нулю в эпоху (путем выбора соответствующего определения эпохи), оставляя указать только пять других орбитальных элементов.

Для разных астрономических тел используются разные наборы элементов. Эксцентриситет e и большая полуось a или расстояние перицентра q используются для определения формы и размера орбиты. Долгота восходящего узла Ω , наклонение i и аргумент перицентра ω или долгота перицентра ϖ определяют ориентацию орбиты в ее плоскости. Для указания известной точки на орбите используются либо долгота в эпоху L ₀ , средняя аномалия в эпоху M ₀ или время прохождения перигелия T _{0 .} Сделанный выбор зависит от того, используется ли весеннее равноденствие или узел в качестве основной точки отсчета. Большая полуось известна, если известны среднее движение и гравитационная масса . ^{[2] [3]}

Также довольно часто можно увидеть либо среднюю аномалию ( M ), либо среднюю долготу ( L ), выраженную напрямую, без M ₀ или L ₀ в качестве промежуточных шагов, как полиномиальную функцию по времени. Этот метод выражения объединит среднее движение ( n ) в полином в качестве одного из коэффициентов. Будет казаться, что L или M выражаются более сложным образом, но нам понадобится на один орбитальный элемент меньше.

Среднее движение также может быть скрыто за ссылками на орбитальный период P. ^{[ нужны разъяснения ]}

Преобразования угла Эйлера

Углы Ω , i , ω — это углы Эйлера (соответствующие α , β , γ в обозначениях, используемых в этой статье), характеризующие ориентацию системы координат.

x̂ , ŷ , ẑ от инерциальной системы координат Î , Ĵ , K̂

где:

• Î , Ĵ находится в экваториальной плоскости центрального тела. Î находится в направлении точки весеннего равноденствия. Ĵ перпендикулярен Î и вместе с Î определяет базовую плоскость. K̂ перпендикулярен базовой плоскости. Орбитальные элементы тел (планет, комет, астероидов...) в Солнечной системе обычно представляют собой плоскость эклиптики .
• x̂ , ŷ находятся в плоскости орбиты и с x̂ в направлении к перицентру ( периапсису ). ẑ перпендикулярен плоскости орбиты. ŷ взаимно перпендикулярен x̂ и ẑ .

Тогда преобразование из системы координат Î , Ĵ , K̂ в систему координат x̂ , ŷ , ẑ с углами Эйлера Ω , i , ω :

$${\displaystyle {\begin{aligned}x_{1}&=\cos \Omega \cdot \cos \omega -\sin \Omega \cdot \cos i\cdot \sin \omega \ ;\\x_{2}&=\sin \Omega \cdot \cos \omega +\cos \Omega \cdot \cos i\cdot \sin \omega \ ;\\x_{3}&=\sin i\cdot \sin \omega ;\\\,\\y_{1}&=-\cos \Omega \cdot \sin \omega -\sin \Omega \cdot \cos i\cdot \cos \omega \ ;\\y_{2}&=-\sin \Omega \cdot \sin \omega +\cos \Omega \cdot \cos i\cdot \cos \omega \ ;\\y_{3}&=\sin i\cdot \cos \omega \ ;\\\,\\z_{1}&=\sin i\cdot \sin \Omega \ ;\\z_{2}&=-\sin i\cdot \cos \Omega \ ;\\z_{3}&=\cos i\ ;\\\end{aligned}}}$$

$${\displaystyle {\begin{bmatrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\z_{1}&z_{2}&z_{3}\end{bmatrix}}={\begin{bmatrix}\cos \omega &\sin \omega &0\\-\sin \omega &\cos \omega &0\\0&0&1\end{bmatrix}}\,{\begin{bmatrix}1&0&0\\0&\cos i&\sin i\\0&-\sin i&\cos i\end{bmatrix}}\,{\begin{bmatrix}\cos \Omega &\sin \Omega &0\\-\sin \Omega &\cos \Omega &0\\0&0&1\end{bmatrix}}\,;}$$

$${\displaystyle {\begin{aligned}\mathbf {\hat {x}} &=x_{1}\mathbf {\hat {I}} +x_{2}\mathbf {\hat {J}} +x_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {y}} &=y_{1}\mathbf {\hat {I}} +y_{2}\mathbf {\hat {J}} +y_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {z}} &=z_{1}\mathbf {\hat {I}} +z_{2}\mathbf {\hat {J}} +z_{3}\mathbf {\hat {K}} ~.\\\end{aligned}}}$$

Обратное преобразование, которое вычисляет 3 координаты в системе IJK по 3 (или 2) координатам в системе xyz, представлено обратной матрицей. Согласно правилам матричной алгебры , обратная матрица произведения трех матриц вращения получается путем инвертирования порядка трех матриц и переключения знаков трех углов Эйлера.

Преобразование x̂ , ŷ , ẑ в углы Эйлера Ω , i , ω :

$${\displaystyle {\begin{aligned}\Omega &=\operatorname {arg} \left(-z_{2},z_{1}\right)\\i&=\operatorname {arg} \left(z_{3},{\sqrt {{z_{1}}^{2}+{z_{2}}^{2}}}\right)\\\omega &=\operatorname {arg} \left(y_{3},x_{3}\right)\\\end{aligned}}}$$

arg( x , y )atan2(y,x),

Прогноз орбиты

В идеальных условиях идеально сферического центрального тела, нулевых возмущений и незначительных релятивистских эффектов все элементы орбиты, за исключением средней аномалии, являются постоянными. Средняя аномалия изменяется линейно со временем, масштабируясь по среднему движению ^[2]

$${\displaystyle n={\sqrt {\frac {\mu }{a^{3}}}}.}$$

цстандартный гравитационный параметрt ₀( e ₀ , a ₀ , i ₀ , Ω ₀ , ω ₀ , M ₀ )t = t ₀ + δt( e ₀ , a ₀ , я ₀ , Ω ₀ , ω ₀ , M ₀ + п δt )

Возмущения и элементарная дисперсия

Невозмущенные двухчастичные ньютоновские орбиты всегда представляют собой конические сечения , поэтому кеплеровы элементы определяют эллипс , параболу или гиперболу . Реальные орбиты имеют возмущения, поэтому данный набор кеплеровских элементов точно описывает орбиту только в данную эпоху. Эволюция элементов орбит происходит за счет гравитационного притяжения тел, отличных от главного, несферичности главного, атмосферного сопротивления , релятивистских эффектов , радиационного давления , электромагнитных сил и так далее.

Кеплеровские элементы часто можно использовать для получения полезных предсказаний в моменты, близкие к эпохе. Альтернативно, реальные траектории можно смоделировать как последовательность кеплеровских орбит, которые соприкасаются («целуют» или касаются) реальной траектории. Их также можно описать так называемыми планетарными уравнениями, дифференциальными уравнениями, которые имеют различные формы, разработанные Лагранжем , Гауссом , Делоне , Пуанкаре или Хиллом .

Двухлинейные элементы

Параметры кеплеровских элементов могут быть закодированы в виде текста в нескольких форматах. Наиболее распространенным из них является формат «двухстрочных элементов» (TLE) НАСА / НОРАД ^[4] , первоначально разработанный для использования с перфокартами с 80 столбцами, но до сих пор используемый, поскольку это наиболее распространенный формат, и с ним можно работать. легко со всеми современными хранилищами данных.

В зависимости от приложения и орбиты объекта данные, полученные из TLE старше 30 дней, могут стать ненадежными. Орбитальные позиции можно рассчитать на основе TLE с помощью алгоритмов SGP/ SGP4 / SDP4 /SGP8/SDP8. ^[5]

Пример двухстрочного элемента: ^[6]

1 27651U 03004A 07083.49636287 .00000119 00000-0 30706-4 0 26922 27651 039.9951 132.2059 0025931 073.4582 286.9047 14.81909376225249

Переменные Делоне

Элементы орбиты Делоне были введены Шарлем-Эженом Делоне во время его изучения движения Луны . ^[7] Обычно называемые переменными Делоне , они представляют собой набор канонических переменных , которые являются координатами действие-угол . Углы представляют собой простые суммы некоторых кеплеровских углов:

• средняя долгота : ${\displaystyle \ell =M+\omega +\Omega \,,}$
• долгота периапсиса : и ${\displaystyle g=\omega +\Omega \,,}$
• долгота восходящего узла : ${\displaystyle h=\Omega }$

вместе с соответствующими им сопряженными импульсами L , G и H. ^[8] Импульсы L , G и H являются переменными действия и представляют собой более сложные комбинации кеплеровских элементов a , e и i .

Переменные Делоне используются для упрощения пертурбативных вычислений в небесной механике, например, при исследовании колебаний Козаи – Лидова в иерархических тройных системах. ^[8] Преимущество переменных Делоне состоит в том, что они остаются четко определенными и неособыми (за исключением h , с которым можно мириться), когда e и/или i очень малы: Когда орбита пробной частицы очень близка к круговой ( ) , или почти «плоский» ( ). ${\displaystyle e\approx 0}$ ${\displaystyle i\approx 0}$

Смотрите также

• Видимая долгота
• Семейство астероидов — астероиды, имеющие схожие элементы собственных орбит.
• Бета-угол
• Эфемериды
• Геопотенциальная модель
• Наклонение орбиты
• Векторы состояния орбиты
• Собственные элементы орбиты
• Соприкасающаяся орбита

Рекомендации

1. Например, с «VEC2TLE». amsat.org . Архивировано из оригинала 20 мая 2016 года . Проверено 19 июня 2013 г.
2. Грин, Робин М. (1985). Сферическая астрономия . Издательство Кембриджского университета. ISBN 978-0-521-23988-2.
3. Дэнби, JMA (1962). Основы небесной механики . Вильманн-Белл. ISBN 978-0-943396-20-0.
4. Келсо, Т.С. «Часто задаваемые вопросы: формат набора двухстрочных элементов». celestrak.com . СелесТрак. Архивировано из оригинала 26 марта 2016 года . Проверено 15 июня 2016 г.
5. Зайдельманн, КП, изд. (1992). Пояснительное приложение к Астрономическому альманаху (1-е изд.). Милл-Вэлли, Калифорния: Университетские научные книги.
6. "ИСТНИК". Heavens-Above.com . данные об орбите. Архивировано из оригинала 27 сентября 2007 года.
7. Обен, Дэвид (2014). «Делоне, Шарль-Эжен». Биографическая энциклопедия астрономов . Нью-Йорк, штат Нью-Йорк: Springer New York. стр. 548–549. дои : 10.1007/978-1-4419-9917-7_347. ISBN 978-1-4419-9916-0.
8. Шевченко, Иван (2017). Эффект Лидова-Козаи: применение в исследовании экзопланет и динамической астрономии . Чам: Спрингер. ISBN 978-3-319-43522-0.

Внешние ссылки

• Гурфил, Пини (2005). «Параметры Эйлера как неособые орбитальные элементы на околоэкваториальных орбитах». Дж. Гид. Контроль. Динамика . 28 (5): 1079–1084. Бибкод : 2005JGCD...28.1079G. дои : 10.2514/1.14760.

• "Руководство". АМСАТ . Кеплеровы элементы. Архивировано из оригинала 14 октября 2002 года.

• «Учебник по орбитам». Marine.rutgers.edu . Архивировано из оригинала 19 апреля 2021 года . Проверено 30 июля 2019 г.

• «Визуализатор элементов орбиты». www.orbitalmechanics.info .

• Отчет №3 (PDF) . целестрак (Отчет). Космический трек. Командование воздушно-космической обороны Северной Америки (НОРАД). Архивировано (PDF) из оригинала 3 сентября 2000 года.— серьезная обработка элементов орбиты

• "ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ". Целестрак . Двухлинейные элементы. Архивировано из оригинала 26 марта 2016 года.

• «Онлайн-эфемериды JPL HORIZONS».- также предоставляет орбитальные элементы для большого количества объектов Солнечной системы.

• «Средние параметры орбиты». ssd.jpl.nasa.gov . Планетарные спутники. Лаборатория реактивного движения / НАСА.

• «Введение в экспорт». ssd.jpl.nasa.gov . Планетарные и лунные эфемериды JPL. Лаборатория реактивного движения / НАСА.

• «Векторы состояния: VEC2TLE». MindSpring (программное обеспечение). Архивировано из оригинала 3 марта 2016 года.– доступ к программному обеспечению VEC2TLE

• «Функция 'iauPlan94'» ( исходный код программного обеспечения C ). Библиотека IAU SOFA C.– элементы орбит больших планет