Центр масс

Уникальная точка, в которой взвешенное относительное положение распределенной массы в сумме равно нулю

Эта игрушка использует принцип центра масс для сохранения равновесия, сидя на пальце.

В физике центр масс распределения массы в пространстве (иногда называемый барицентром или точкой равновесия ) — это уникальная точка в любой момент времени, где взвешенное относительное положение распределенной массы в сумме равно нулю. Это точка, к которой может быть приложена сила, чтобы вызвать линейное ускорение без углового ускорения . Расчеты в механике часто упрощаются, когда формулируются относительно центра масс. Это гипотетическая точка, где можно предположить, что вся масса объекта сосредоточена, чтобы визуализировать его движение. Другими словами, центр масс — это эквивалент частицы данного объекта для применения законов движения Ньютона . ^[1]

В случае одного твердого тела центр масс фиксирован относительно тела, и если тело имеет однородную плотность , он будет расположен в центроиде . Центр масс может быть расположен вне физического тела , как это иногда бывает для полых или открытых по форме объектов, таких как подкова . В случае распределения отдельных тел, таких как планеты Солнечной системы , центр масс может не соответствовать положению любого отдельного члена системы.

Центр масс является полезной точкой отсчета для расчетов в механике , которые включают массы, распределенные в пространстве, такие как линейный и угловой импульс планетарных тел и динамика твердого тела . В орбитальной механике уравнения движения планет формулируются как точечные массы, расположенные в центрах масс ( подробнее см. Барицентр (астрономия) ). Система центра масс — это инерциальная система , в которой центр масс системы находится в состоянии покоя относительно начала системы координат .

История

Концепция центра тяжести или веса была подробно изучена древнегреческим математиком , физиком и инженером Архимедом из Сиракуз . Он работал с упрощенными предположениями о гравитации, которые представляют собой однородное поле, таким образом, придя к математическим свойствам того, что мы сейчас называем центром масс. Архимед показал, что крутящий момент, оказываемый на рычаг грузами, покоящимися в различных точках вдоль рычага, такой же, как если бы все грузы были перемещены в одну точку — их центр масс. В своей работе « О плавающих телах » Архимед продемонстрировал, что ориентация плавающего объекта — это та, которая делает его центр масс как можно ниже. Он разработал математические методы для нахождения центров масс объектов однородной плотности различных четко определенных форм. ^[2]

Другие древние математики, которые внесли свой вклад в теорию центра масс, включают Герона Александрийского и Паппа Александрийского . В эпоху Возрождения и раннего Нового времени работы Гвидо Убальди , Франческо Мавролико , ^[3] Федерико Коммандино , ^[4] Эванджелиста Торричелли , Саймона Стевина , ^[5] Луки Валерио , ^[6] Жана-Шарля де ла Файля , Поля Гулдина , ^[7] Джона Уоллиса , Христиана Гюйгенса , ^[8] Луи Карре , Пьера Вариньона и Алексиса Клеро еще больше расширили эту концепцию. ^[9]

Второй закон Ньютона переформулирован относительно центра масс в первом законе Эйлера . ^[10]

Определение

Центр масс — это уникальная точка в центре распределения масс в пространстве, которая обладает свойством, что взвешенные векторы положения относительно этой точки в сумме равны нулю. По аналогии со статистикой, центр масс — это среднее местоположение распределения масс в пространстве.

Система частиц

В случае системы частиц P _i , i = 1, ...,  n  , каждая из которых имеет массу m _i , расположенных в пространстве с координатами r _i , i = 1, ...,  n  , координаты R центра масс удовлетворяют ∑ i = 1 n m i ( r i − R ) = 0 . {\displaystyle \sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )=\mathbf {0} .}

Решение этого уравнения относительно R дает формулу R = ∑ i = 1 n m i r i ∑ i = 1 n m i . {\displaystyle \mathbf {R} ={\sum _{i=1}^{n}m_{i}\mathbf {r} _{i} \over \sum _{i=1}^{n}m_{i}}.}

Непрерывный объем

Если распределение массы непрерывно с плотностью ρ( r ) внутри твердого тела Q , то интеграл взвешенных координат положения точек в этом объеме относительно центра масс R по объему V равен нулю, то есть $${\displaystyle \iiint _{Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV=0.}$$

Решите это уравнение относительно координат R , чтобы получить Где M — общая масса в объеме. $${\displaystyle \mathbf {R} ={\frac {1}{M}}\iiint _{Q}\rho (\mathbf {r} )\mathbf {r} \,dV,}$$

Если непрерывное распределение массы имеет равномерную плотность , что означает, что ρ является постоянным, то центр масс совпадает с центроидом объема. ^[11]

Барицентрические координаты

Координаты R центра масс двухчастичной системы P ₁ и P ₂ с массами m ₁ и m ₂ определяются выражением: $${\displaystyle \mathbf {R} ={{m_{1}\mathbf {r} _{1}+m_{2}\mathbf {r} _{2}} \over m_{1}+m_{2}}.}$$

Пусть процент общей массы, разделенный между этими двумя частицами, изменяется от 100% P ₁ и 0% P ₂ до 50% P ₁ и 50% P ₂ до 0% P ₁ и 100% P ₂ , тогда центр масс R перемещается вдоль линии от P ₁ до P ₂ . Проценты массы в каждой точке можно рассматривать как проективные координаты точки R на этой линии и называются барицентрическими координатами . Другой способ интерпретации процесса здесь - механическое уравновешивание моментов относительно произвольной точки. Числитель дает общий момент, который затем уравновешивается эквивалентной общей силой в центре масс. Это можно обобщить до трех точек и четырех точек, чтобы определить проективные координаты на плоскости и в пространстве соответственно.

Системы с периодическими граничными условиями

Для частиц в системе с периодическими граничными условиями две частицы могут быть соседями, даже если они находятся на противоположных сторонах системы. Это часто происходит в молекулярно-динамических симуляциях, например, в которых кластеры образуются в случайных местах, а иногда соседние атомы пересекают периодическую границу. Когда кластер охватывает периодическую границу, наивный расчет центра масс будет неверным. Обобщенный метод расчета центра масс для периодических систем заключается в том, чтобы рассматривать каждую координату, x и y и/или z , как если бы она находилась на окружности, а не на линии. ^[12] Расчет берет координату x каждой частицы и отображает ее в угол, где x _max — размер системы в направлении x, а . Из этого угла можно сгенерировать две новые точки, которые можно взвесить по массе частицы для центра масс или задать значение 1 для геометрического центра: $${\displaystyle \theta _{i}={\frac {x_{i}}{x_{\max }}}2\pi }$$ ${\displaystyle x_{i}\in [0,x_{\max })}$ ${\displaystyle (\xi _{i},\zeta _{i})}$ ${\displaystyle x_{i}}$ $${\displaystyle {\begin{aligned}\xi _{i}&=\cos(\theta _{i})\\\zeta _{i}&=\sin(\theta _{i})\end{aligned}}}$$

На плоскости эти координаты лежат на окружности радиусом 1. Из совокупности значений и от всех частиц вычисляются средние значения и . ${\displaystyle (\xi ,\zeta )}$ ${\displaystyle \xi _{i}}$ ${\displaystyle \zeta _{i}}$ ${\displaystyle {\overline {\xi }}}$ ${\displaystyle {\overline {\zeta }}}$

$${\displaystyle {\begin{aligned}{\overline {\xi }}&={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\xi _{i},\\{\overline {\zeta }}&={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\zeta _{i},\end{aligned}}}$$где M — сумма масс всех частиц.

Эти значения преобразуются обратно в новый угол, из которого можно получить координату x центра масс: ${\displaystyle {\overline {\theta }}}$

$${\displaystyle {\begin{aligned}{\overline {\theta }}&=\operatorname {atan2} \left(-{\overline {\zeta }},-{\overline {\xi }}\right)+\pi \\x_{\text{com}}&=x_{\max }{\frac {\overline {\theta }}{2\pi }}\end{aligned}}}$$

Процесс можно повторить для всех измерений системы, чтобы определить полный центр масс. Полезность алгоритма в том, что он позволяет математике определить, где находится «лучший» центр масс, вместо того, чтобы угадывать или использовать кластерный анализ для «развертывания» кластера, охватывающего периодические границы. Если оба средних значения равны нулю, то не определено. Это правильный результат, потому что он возникает только тогда, когда все частицы расположены точно равномерно. В этом состоянии их координаты x математически идентичны в периодической системе . ${\displaystyle \left({\overline {\xi }},{\overline {\zeta }}\right)=(0,0)}$ ${\displaystyle {\overline {\theta }}}$

Центр тяжести

Схема развивающей игрушки, которая балансирует на точке: центр масс (С) располагается ниже своей опоры (Р)

Центр тяжести тела — это точка, вокруг которой исчезает результирующий крутящий момент, вызванный силами гравитации. ^[13] Там, где гравитационное поле можно считать однородным, центр масс и центр тяжести будут одинаковыми. Однако для спутников на орбите вокруг планеты, при отсутствии других крутящих моментов, приложенных к спутнику, небольшое изменение (градиент) в гравитационном поле между более близким и более удаленным от планеты (более сильная и более слабая гравитация соответственно) может привести к крутящему моменту, который будет стремиться выровнять спутник таким образом, чтобы его длинная ось была вертикальной. В таком случае важно провести различие между центром тяжести и центром масс. ^[14] Любое горизонтальное смещение между ними приведет к приложенному крутящему моменту.

Центр масс является фиксированным свойством для данного твердого тела (например, без плеска или сочленения), тогда как центр тяжести может, кроме того, зависеть от его ориентации в неоднородном гравитационном поле. В последнем случае центр тяжести всегда будет располагаться несколько ближе к основному притягивающему телу по сравнению с центром масс, и, таким образом, будет менять свое положение в интересующем теле по мере изменения его ориентации.

При изучении динамики самолетов, транспортных средств и судов силы и моменты должны быть разрешены относительно центра масс. Это верно независимо от того, рассматривается ли сама гравитация. Ссылка на центр масс как на центр тяжести является чем-то вроде разговорного выражения, но это общепринятое употребление, и когда эффекты градиента гравитации незначительны, центр тяжести и центр масс являются одним и тем же и используются взаимозаменяемо.

В физике преимущества использования центра масс для моделирования распределения масс можно увидеть, рассмотрев результирующую силу тяжести на непрерывном теле. Рассмотрим тело Q объёма V с плотностью ρ ( r ) в каждой точке r объёма. В параллельном гравитационном поле сила f в каждой точке r определяется как, где dm — масса в точке r , g — ускорение силы тяжести, а — единичный вектор, определяющий вертикальное направление. $${\displaystyle \mathbf {f} (\mathbf {r} )=-dm\,g\mathbf {\hat {k}} =-\rho (\mathbf {r} )\,dV\,g\mathbf {\hat {k}} ,}$$ ${\textstyle \mathbf {\hat {k}} }$

Выберите опорную точку R в объеме и вычислите результирующую силу и крутящий момент в этой точке, F = ∭ Q f ( r ) d V = ∭ Q ρ ( r ) d V ( − g k ^ ) = − M g k ^ , {\displaystyle \mathbf {F} =\iiint _{Q}\mathbf {f} (\mathbf {r} )\,dV=\iiint _{Q}\rho (\mathbf {r} )\,dV\left(-g\mathbf {\hat {k}} \right)=-Mg\mathbf {\hat {k}} ,} и T = ∭ Q ( r − R ) × f ( r ) d V = ∭ Q ( r − R ) × ( − g ρ ( r ) d V k ^ ) = ( ∭ Q ρ ( r ) ( r − R ) d V ) × ( − g k ^ ) . {\displaystyle \mathbf {T} =\iiint _{Q}(\mathbf {r} -\mathbf {R})\times \mathbf {f} (\mathbf {r})\,dV = \iiint _{Q}(\mathbf {r} -\mathbf {R})\times \left(-g\rho (\mathbf {r})\,d V\,\mathbf {\hat {k}} \right)=\left(\iiint _{Q}\rho (\mathbf {r})\left(\mathbf {r} -\mathbf {R} \right)dV\right)\times \left(-g\mathbf {\hat {k}} \right).}

Если опорная точка R выбрана так, что она является центром масс, то это означает, что результирующий крутящий момент T = 0. Поскольку результирующий крутящий момент равен нулю, тело будет двигаться так, как будто оно является частицей, масса которой сосредоточена в центре масс. $${\displaystyle \iiint _{Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV=0,}$$

При выборе центра тяжести в качестве точки отсчета для твердого тела силы тяжести не будут заставлять тело вращаться, а это значит, что вес тела можно считать сосредоточенным в центре масс.

Линейный и угловой момент

Линейный и угловой импульсы совокупности частиц можно упростить, измерив положение и скорость частиц относительно центра масс. Пусть система частиц P _i , i = 1, ..., n масс m _i находится в координатах r _i со скоростями v _i . Выберите точку отсчета R и вычислите векторы относительного положения и скорости, $${\displaystyle \mathbf {r} _{i}=(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {R} ,\quad \mathbf {v} _{i}={\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {v} .}$$

Полный линейный импульс и угловой момент системы равны p = d d t ( ∑ i = 1 n m i ( r i − R ) ) + ( ∑ i = 1 n m i ) v , {\displaystyle \mathbf {p} ={\frac {d}{dt}}\left(\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\right)+\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {v} ,} и L = ∑ i = 1 n m i ( r i − R ) × d d t ( r i − R ) + ( ∑ i = 1 n m i ) [ R × d d t ( r i − R ) + ( r i − R ) × v ] + ( ∑ i = 1 n m i ) R × v {\displaystyle \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\left(\sum _{i=1}^{n}m_{i}\right)\left[\mathbf {R} \times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+(\mathbf {r} _{i}-\mathbf {R} )\times \mathbf {v} \right]+\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {R} \times \mathbf {v} }

Если в качестве центра масс выбрать R, то эти уравнения упрощаются до вида, где m — общая масса всех частиц, p — линейный импульс, а L — угловой момент. $${\displaystyle \mathbf {p} =m\mathbf {v} ,\quad \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\sum _{i=1}^{n}m_{i}\mathbf {R} \times \mathbf {v} }$$

Закон сохранения импульса предсказывает, что для любой системы, не подверженной внешним силам, импульс системы останется постоянным, что означает, что центр масс будет двигаться с постоянной скоростью. Это применимо ко всем системам с классическими внутренними силами, включая магнитные поля, электрические поля, химические реакции и т. д. Более формально, это верно для любых внутренних сил, которые отменяют друг друга в соответствии с Третьим законом Ньютона . ^[15]

Определение

Метод отвеса

Экспериментальное определение центра масс тела осуществляется с использованием сил тяжести, действующих на тело, и основано на том факте, что центр масс совпадает с центром тяжести в параллельном гравитационном поле вблизи поверхности Земли.

Центр масс тела с осью симметрии и постоянной плотностью должен лежать на этой оси. Таким образом, центр масс кругового цилиндра постоянной плотности имеет свой центр масс на оси цилиндра. Точно так же центр масс сферически симметричного тела постоянной плотности находится в центре сферы. В общем случае, для любой симметрии тела, его центр масс будет неподвижной точкой этой симметрии. ^[16]

В двух измерениях

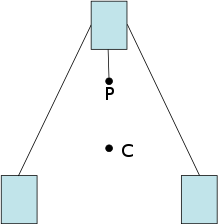
Экспериментальный метод определения центра масс заключается в подвешивании объекта в двух местах и ​​опускании отвесных линий из точек подвеса. Пересечение двух линий является центром масс. ^[17]

Форма объекта может быть уже определена математически, но она может быть слишком сложной для использования известной формулы. В этом случае можно подразделить сложную форму на более простые, более элементарные формы, центры масс которых легко найти. Если общая масса и центр масс могут быть определены для каждой области, то центр масс целого является средневзвешенным значением центров. ^[18] Этот метод может работать даже для объектов с отверстиями, которые можно учитывать как отрицательные массы. ^[19]

Прямое развитие планиметра , известного как интеграграф, или целочисленный метр, может быть использовано для установления положения центроида или центра масс нерегулярной двумерной формы. Этот метод может быть применен к форме с нерегулярной, гладкой или сложной границей, где другие методы слишком сложны. Он регулярно использовался судостроителями для сравнения с требуемым водоизмещением и центром плавучести судна, и для того, чтобы убедиться, что оно не опрокинется. ^{[20] [21]}

В трех измерениях

Экспериментальный метод определения трехмерных координат центра масс начинается с поддержки объекта в трех точках и измерения сил F ₁ , F ₂ и F ₃ , которые противостоят весу объекта ( — единичный вектор в вертикальном направлении). Пусть r ₁ , r ₂ и r ₃ — координаты положения точек опоры, тогда координаты R центра масс удовлетворяют условию, что результирующий крутящий момент равен нулю, или ${\displaystyle \mathbf {W} =-W\mathbf {\hat {k}} }$ ${\displaystyle \mathbf {\hat {k}} }$ $${\displaystyle \mathbf {T} =(\mathbf {r} _{1}-\mathbf {R} )\times \mathbf {F} _{1}+(\mathbf {r} _{2}-\mathbf {R} )\times \mathbf {F} _{2}+(\mathbf {r} _{3}-\mathbf {R} )\times \mathbf {F} _{3}=0,}$$ $${\displaystyle \mathbf {R} \times \left(-W\mathbf {\hat {k}} \right)=\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}.}$$

Это уравнение дает координаты центра масс R * в горизонтальной плоскости как, $${\displaystyle \mathbf {R} ^{*}=-{\frac {1}{W}}\mathbf {\hat {k}} \times (\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}).}$$

Центр масс лежит на вертикальной линии L , заданной формулой $${\displaystyle \mathbf {L} (t)=\mathbf {R} ^{*}+t\mathbf {\hat {k}} .}$$

Трехмерные координаты центра масс определяются путем проведения этого эксперимента дважды с объектом, расположенным таким образом, чтобы эти силы измерялись для двух различных горизонтальных плоскостей, проходящих через объект. Центр масс будет пересечением двух линий L ₁ и L _2, полученных из двух экспериментов.

Приложения

Инженерные проекты

Автомобильные приложения

Инженеры пытаются спроектировать спортивный автомобиль так, чтобы его центр масс был ниже, что позволит улучшить управляемость автомобиля , то есть сохранить сцепление с дорогой при выполнении относительно крутых поворотов.

Характерный низкий профиль американского военного автомобиля Humvee был разработан отчасти для того, чтобы он мог наклоняться больше, чем более высокие транспортные средства, не переворачиваясь , гарантируя, что его низкий центр масс остается над пространством, ограниченным четырьмя колесами, даже под углами, далекими от горизонтали .

Аэронавтика

Центр масс является важной точкой на самолете , которая существенно влияет на устойчивость самолета. Чтобы гарантировать, что самолет достаточно устойчив для безопасного полета, центр масс должен находиться в определенных пределах. Если центр масс находится впереди переднего предела , самолет будет менее маневренным, возможно, до такой степени, что он не сможет вращаться для взлета или выравнивания для посадки. ^[22] Если центр масс находится позади заднего предела, самолет будет более маневренным, но также менее устойчивым и, возможно, достаточно неустойчивым, чтобы летать. Плечо момента руля высоты также будет уменьшено, что затрудняет выход из состояния сваливания . ^[23]

Для вертолетов в режиме зависания центр масс всегда находится прямо под головкой ротора . В прямом полете центр масс будет двигаться вперед, чтобы уравновесить отрицательный крутящий момент тангажа, создаваемый применением циклического управления для продвижения вертолета вперед; следовательно, крейсерский вертолет летит «носом вниз» в горизонтальном полете. ^[24]

Астрономия

Два тела, вращающиеся вокруг своего барицентра (красный крест)

Центр масс играет важную роль в астрономии и астрофизике, где его обычно называют барицентром . Барицентр — это точка между двумя объектами, где они уравновешивают друг друга; это центр масс, где два или более небесных тела вращаются вокруг друг друга. Когда луна вращается вокруг планеты , или планета вращается вокруг звезды , оба тела фактически вращаются вокруг точки, которая находится вдали от центра основного (большего) тела. ^[25] Например, Луна вращается не вокруг точного центра Земли , а вокруг точки на линии между центром Земли и Луной, примерно в 1710 км (1062 мили) под поверхностью Земли, где их соответствующие массы уравновешивают друг друга. Это точка, вокруг которой вращаются Земля и Луна, когда они движутся вокруг Солнца . Если массы более схожи, например, Плутон и Харон , барицентр будет находиться за пределами обоих тел.

Оснастка и безопасность

Знание расположения центра тяжести при такелажных работах имеет решающее значение, что может привести к серьезным травмам или смерти, если неправильно принять его. Центр тяжести, который находится в точке подъема или выше, скорее всего, приведет к опрокидыванию. В общем, чем дальше центр тяжести ниже точки захвата, тем безопаснее подъем. Есть и другие факторы, которые следует учитывать, такие как смещение грузов, прочность груза и масса, расстояние между точками захвата и количество точек захвата. В частности, при выборе точек подъема очень важно разместить центр тяжести в центре и значительно ниже точек подъема. ^[26]

Движение тела

В кинезиологии и биомеханике центр масс является важным параметром, который помогает людям понять их локомоцию. Обычно центр масс человека определяется одним из двух методов: метод реакционной доски представляет собой статический анализ, который включает в себя человека, лежащего на этом инструменте, и использование его уравнения статического равновесия для нахождения его центра масс; метод сегментации опирается на математическое решение, основанное на физическом принципе , что сумма моментов сил отдельных частей тела относительно указанной оси должна равняться моменту сил всей системы, составляющей тело, измеренному относительно той же оси. ^[27]

Оптимизация

Метод центра тяжести — это метод выпуклой оптимизации, который использует центр тяжести допустимой области.

Смотрите также

• Физический портал

• Барицентр
• Плавучесть
• Центр удара
• Центр давления (механика жидкости)
• Центр давления (наземное передвижение)
• Центроид
• Окружностьцентр масс
• Ожидаемое значение
• Геометрия точечной массы
• Метацентрическая высота
• Центр рулона
• Распределение веса

Примечания

1. "10.3: Центр масс". Physics LibreTexts . 17 сентября 2019 г. Получено 15 октября 2024 г.
2. Шор 2008, стр. 9–11.
3. Барон 2004, стр. 91–94.
4. Барон 2004, стр. 94–96.
5. Барон 2004, стр. 96–101.
6. Барон 2004, стр. 101–106.
7. Манкосу 1999, стр. 56–61.
8. Эрлихсон, Х. (1996). «Открытие формулы центра колебаний Христианом Гюйгенсом». American Journal of Physics . 64 (5): 571–574. Bibcode : 1996AmJPh..64..571E. doi : 10.1119/1.18156. ISSN  0002-9505.
9. Уолтон 1855, стр. 2.
10. Битти 2006, стр. 29.
11. Леви 2009, стр. 85.
12. Бай и Брин 2008.
13. Резник, Р. и Холлидей, Д. (1962) Физика , 9-1 «Центр масс», Wiley
14. Резник, Р. и Холлидей, Д. (1962) Физика , 14-3 «Центр тяжести», Wiley
15. Клеппнер и Коленков 1973, с. 117.
16. Фейнмановские лекции по физике, том I, гл. 19: Центр масс; Момент инерции
17. Клеппнер и Коленков 1973, стр. 119–120.
18. Фейнман, Лейтон и Сэндс 1963, стр. 19.1–19.2.
19. Хэмилл 2009, стр. 20–21.
20. "Теория и проектирование британского судостроения". Амос Лоури Эйр . стр. 3. Получено 20 августа 2012 г.
21. Сангвин 2006, стр. 7.
22. Федеральное управление гражданской авиации, 2007 г., стр. 1.4.
23. Федеральное управление гражданской авиации, 2007 г., стр. 1.3.
24. "Аэродинамика вертолета" (PDF) . стр. 82. Архивировано из оригинала (PDF) 2012-03-24 . Получено 2013-11-23 .
25. Мюррей и Дермотт 1999, стр. 45–47.
26. "Structural Collapse Technician: Module 4 - Lifting and Rigging" (PDF) . FEMA.gov . Получено 27.11.2019 .
27. Винт 2003, стр. 1–11.

Ссылки

• Азимов, Айзек (1988) [1966], Понимание физики , Barnes & Noble Books, ISBN 978-0-88029-251-1
• Бай, Линге; Брин, Дэвид (2008). «Вычисление центра масс в неограниченной двумерной среде». Журнал графики, графических процессоров и игровых инструментов . 13 (4): 53–60. doi :10.1080/2151237X.2008.10129266. S2CID  40807367.
• Барон, Маргарет Э. (2004) [1969], Происхождение исчисления бесконечно малых величин , Courier Dover Publications, ISBN 978-0-486-49544-6
• Битти, Миллард Ф. (2006), Принципы инженерной механики, том 2: Динамика — Анализ движения , Математические концепции и методы в науке и технике, т. 33, Springer, ISBN 978-0-387-23704-6
• Де Сильва, Кларенс В. (2002), Справочник по вибрации и ударам , CRC Press, ISBN 978-0-8493-1580-0
• Федеральное управление гражданской авиации (2007), Справочник по весу и балансировке воздушных судов (PDF) , Типография правительства США , архивировано из оригинала (PDF) 2011-10-19 , извлечено 2011-10-23
• Фейнман, Ричард ; Лейтон, Роберт Б.; Сэндс , Мэтью (1963), Лекции Фейнмана по физике , т. 1 (шестое издание, февраль 1977 г.), Addison-Wesley, ISBN 978-0-201-02010-6
• Фраучи, Стивен К .; Оленик, Ричард П.; Апостол, Том М.; Гудштейн , Дэвид Л. (1986), Механическая вселенная: механика и тепло, расширенное издание , Cambridge University Press, ISBN 978-0-521-30432-0
• Джамбаттиста, Алан; Ричардсон, Бетти Маккарти; Ричардсон, Роберт Коулман (2007), College physics, т. 1 (2-е изд.), McGraw-Hill Higher Education, ISBN 978-0-07-110608-5
• Голдштейн, Герберт ; Пул, Чарльз; Сафко, Джон (2001), Классическая механика (3-е изд.), Эддисон Уэсли, ISBN 978-0-201-65702-9
• Голдштейн, Герберт ; Пул, Чарльз; Сафко, Джон (2002), Классическая механика (3-е изд.), Addison-Wesley, ISBN 978-0-201-65702-9
• Гудман, Лоуренс Э.; Уорнер, Уильям Х. (2001) [1964], Статика , Довер, ISBN 978-0-486-42005-9
• Хэмилл, Патрик (2009), Промежуточная динамика , Jones & Bartlett Learning, ISBN 978-0-7637-5728-1
• Йонг, И.Г.; Роджерс, Б.Г. (1995), Инженерная механика: Статика , Saunders College Publishing, ISBN 978-0-03-026309-5
• Клеппнер, Дэниел ; Коленков, Роберт (1973), Введение в механику (2-е изд.), McGraw-Hill, ISBN 978-0-07-035048-9
• Леви, Марк (2009), Математическая механика: использование физических рассуждений для решения проблем, Princeton University Press, ISBN 978-0-691-14020-9
• Манкосу, Паоло (1999), Философия математики и математическая практика в семнадцатом веке , Oxford University Press, ISBN 978-0-19-513244-1
• Милликен, Роберт Эндрюс (1902), Механика, молекулярная физика и тепло: двенадцатинедельный курс в колледже, Чикаго: Scott, Foresman and Company , получено 25.05.2011
• Мюррей, Карл; Дермотт, Стэнли (1999), Динамика солнечной системы , Cambridge University Press, ISBN 978-0-521-57295-8
• О'Доннелл, Питер Дж. (2015), Essential Dynamics and Relativity , CRC Press, ISBN 978-1-466-58839-4
• Поллард, Дэвид Д.; Флетчер, Рэймонд К. (2005), Основы структурной геологии , Cambridge University Press, ISBN 978-0-521-83927-3
• Пытель, Эндрю; Киусалаас, Яан (2010), Инженерная механика: Статика , т. 1 (3-е изд.), Cengage Learning, ISBN 978-0-495-29559-4
• Розен, Джо; Готхард, Лиза Куинн (2009), Энциклопедия физических наук , Infobase Publishing, ISBN 978-0-8160-7011-4
• Сангвин, Кристофер Дж. (2006), «Определение центра масс механическими средствами» (PDF) , Журнал Oughtred Society , 15 (2), архивировано из оригинала (PDF) 2011-10-05 , извлечено 2011-10-23
• Serway, Raymond A.; Jewett, John W. (2006), Principles of physics: a calculus-based text , т. 1 (4-е изд.), Thomson Learning, Bibcode : 2006ppcb.book.....J, ISBN 978-0-534-49143-7
• Ширли, Джеймс Х.; Фэрбридж, Родс Уитмор (1997), Энциклопедия планетарных наук , Springer, ISBN 978-0-412-06951-2
• Шор, Стивен Н. (2008), Силы в физике: историческая перспектива , Greenwood Press, ISBN 978-0-313-33303-3
• Саймон, Кит Р. (1971), Механика (3-е изд.), Addison-Wesley, ISBN 978-0-201-07392-8
• Типлер, Пол А.; Моска, Джин (2004), Физика для ученых и инженеров , т. 1A (5-е изд.), WH Freeman and Company, ISBN 978-0-7167-0900-8
• Ван Пелт, Майкл (2005), Космический туризм: приключения на околоземной орбите и за ее пределами , Springer, ISBN 978-0-387-40213-0
• Винт, Питер (2003), "LAB: Центр масс (центр тяжести) человеческого тела" (PDF) , KIN 335 - Биомеханика , получено 18 октября 2013 г.
• Уолтон, Уильям (1855), Сборник задач, иллюстрирующих принципы теоретической механики (2-е изд.), Deighton, Bell & Co.

Внешние ссылки

• Движение центра масс показывает, что движение центра масс объекта, находящегося в свободном падении, такое же, как движение точечного объекта.
• Барицентр Солнечной системы, моделирование, показывающее влияние каждой планеты на барицентр Солнечной системы.