stringtranslate.com

Саймон Стевин

Симон Стевин ( голландский: [ˈsimɔn steːˈvɪn] ; 1548–1620), иногда называемый Стевинусом , был фламандским математиком , учёным и теоретиком музыки . [1] Он внёс различный вклад во многие области науки и техники , как теоретические, так и практические. Он также перевёл различные математические термины на голландский язык , сделав его одним из немногих европейских языков, в которых слово для математики , wiskunde ( wis и kunde , т. е. «знание того, что достоверно»), было не заимствованным из греческого , а калькой через латынь . Он также заменил слово chemie , голландское для химии, на scheikunde («искусство разделения»), по аналогии с wiskunde .

Биография

О жизни Симона Стевина известно очень мало достоверно, и то, что мы знаем, в основном выведено из других зафиксированных фактов. [2] Точная дата рождения, а также дата и место его смерти неизвестны. Предполагается, что он родился в Брюгге , поскольку он поступил в Лейденский университет под именем Симон Стевинус да Бругенсис (что означает «Симон Стевин из Брюгге»). Его имя обычно пишется как Стевин, но некоторые документы, касающиеся его отца, используют написание Стевийн (произношение [ˈste:vεɪn]); это было распространенным изменением написания в голландском языке XVI века. [3] Мать Симона Стевина, Кателийн (или Кейтлин), была дочерью богатой семьи из Ипра ; ее отец Хуберт был бедняком из Брюгге. Cathelijne позже вышла замуж за Joost Sayon, который занимался торговлей коврами и шелком и был членом schuttersgilde Sint -Sebastiaan. Благодаря своему браку Cathelijne стала членом семьи кальвинистов ; считается, что Simon Stevin, вероятно, был воспитан в кальвинистской вере. [4]

Считается, что Стевин вырос в относительно обеспеченной среде и получил хорошее образование. Вероятно, он получил образование в латинской школе в своем родном городе. [5]

Путешествия Саймона Стевина

Стевин покинул Брюгге в 1571 году, по-видимому, без определенной цели. Стевин, скорее всего, был кальвинистом, поскольку католик , скорее всего, не достиг бы той должности, которую он позже занял у Морица, принца Оранского . Предполагается, что он покинул Брюгге, чтобы избежать религиозных преследований протестантов испанскими правителями. На основании ссылок в его работе «Wisconstighe Ghedaechtenissen» (Математические мемуары) был сделан вывод, что он, должно быть, сначала переехал в Антверпен, где начал свою карьеру в качестве клерка у торговца . [6] Некоторые биографы упоминают, что он путешествовал по Пруссии , Польше , Дании , Норвегии и Швеции и другим частям Северной Европы между 1571 и 1577 годами. Возможно, что он совершил эти путешествия в течение более длительного периода времени. В 1577 году Симон Стевин вернулся в Брюгге и был назначен городским клерком олдерменами Брюгге, эту должность он занимал с 1577 по 1581 год . Он работал в офисе Яна де Бруна из Brugse Vrije , кастелянства Брюгге.

Неясно, почему он вернулся в Брюгге в 1577 году. Возможно, это было связано с политическими событиями того периода. Брюгге был ареной интенсивного религиозного конфликта. Католики и кальвинисты попеременно контролировали правительство города. Обычно они выступали друг против друга, но иногда сотрудничали, чтобы противостоять диктату короля Филиппа II Испанского . В 1576 году был установлен определенный уровень официальной религиозной терпимости. Это могло бы объяснить, почему Стевин вернулся в Брюгге в 1577 году. Позже кальвинисты захватили власть во многих фламандских городах и заключили в тюрьму католических священнослужителей и светских губернаторов, поддерживавших испанских правителей. Между 1578 и 1584 годами Брюгге управляли кальвинисты.

Саймон Стевин в Нидерландах

В 1581 году Стевин снова покинул родной Брюгге и переехал в Лейден , где посещал латинскую школу. [5] 16 февраля 1583 года он поступил под именем Симон Стевинус Бругенсис (что означает «Симон Стевин из Брюгге») в Лейденский университет , основанный Вильгельмом Молчаливым в 1575 году. Здесь он подружился со вторым сыном Вильгельма Молчаливого и его наследником принцем Морицем , графом Нассау. [4] Стевин указан в реестрах университета до 1590 года и, по-видимому, так и не окончил его.

После убийства Вильгельма Молчаливого и вступления принца Морица на должность отца, Стевин стал главным советником и наставником принца Морица. Принц Мориц много раз спрашивал его совета и сделал его государственным служащим — сначала директором так называемого «waterstaet» [7] (правительственного органа по общественным работам , особенно по управлению водными ресурсами) с 1592 года, а затем генеральным квартирмейстером армии Генеральных штатов. [8] Принц Мориц также попросил Стевина основать инженерную школу в Лейденском университете.

Стевин переехал в Гаагу , где купил дом в 1612 году. Он женился в 1610 или 1614 году и имел четверых детей. Известно, что он оставил вдову с двумя детьми после своей смерти в Лейдене или Гааге в 1620 году. [4]

Нидерландский исследовательский совет (NWO) учредил в 2018 году научную премию имени Стевина — Премию Стевина , которая присуждается за вклад, сокращающий разрыв между научными исследованиями и практическими применениями, приносящими пользу обществу. [9]

Открытия и изобретения

Ветряная колесница или сухопутная яхта (Zeilwagen), спроектированная Симоном Стевиным для принца Морица Оранского (гравюра Жака де Гейна).

Стевин ответственен за множество открытий и изобретений. Стевин написал множество бестселлеров и был пионером в развитии и практическом применении (инженерных) наук, таких как математика , физика и прикладных наук, таких как гидротехника и геодезия . Считалось, что он изобрел десятичные дроби до середины 20-го века, пока исследователи не обнаружили, что десятичные дроби были ранее введены средневековым исламским ученым аль-Уклидиси в книге, написанной в 952 году. Более того, систематическое развитие десятичных дробей было дано задолго до Стевина в книге Miftah al-Hisab, написанной в 1427 году Аль-Каши .

Его современники были больше всего поражены его изобретением так называемой сухопутной яхты , экипажа с парусами, модель которого сохранялась в Схевенингене до 1802 года. Сам экипаж был утерян задолго до этого. Около 1600 года Стевин с принцем Морицем Оранским и двадцатью шестью другими людьми использовали экипаж на пляже между Схевенингеном и Петтеном . Экипаж приводился в движение исключительно силой ветра и приобретал скорость, которая превышала скорость лошадей. [7]

Управление водными путями

Работа Стевина в области водного хозяйства включала усовершенствования шлюзов и водосбросов для контроля за наводнениями , упражнения по гидротехнике . Ветряные мельницы уже использовались для откачки воды, но в работе Ван де Моленса ( О мельницах ) он предложил усовершенствования, включая идеи о том, что колеса должны двигаться медленно с лучшей системой зацепления зубьев шестерен . Это в три раза повысило эффективность ветряных мельниц, используемых для откачки воды из польдеров . [10] Он получил патент на свое нововведение в 1586 году. [8]

Философия науки

Целью Стевина было вызвать вторую эпоху мудрости , в которой человечество восстановило бы все свои ранние знания. Он пришел к выводу, что языком, на котором говорили в эту эпоху, должен был быть голландский, потому что, как он показал эмпирически , в этом языке больше понятий можно было обозначить односложными словами, чем в любом из (европейских) языков, с которыми он его сравнивал. [7] Это было одной из причин, по которой он написал все свои работы на голландском языке и оставил их перевод другим. Другая причина заключалась в том, что он хотел, чтобы его работы были практически полезны людям, которые не овладели общепринятым научным языком того времени, латынью. Благодаря Симону Стевину голландский язык получил свой собственный научный словарь, такой как «wiskunde» ( «kunst van het gewisse of zekere» — искусство того, что известно или что достоверно) для математики , «natuurkunde» («искусство природы») для физики , «scheikunde» («искусство разделения») для химии , «sterrenkunde» («искусство звезд») для астрономии , «meetkunde» («искусство измерения») для геометрии .

Геометрия, физика и тригонометрия

Доказательство Стевина закона равновесия на наклонной плоскости , известное как «Эпитафия Стевина».

Стевин был первым, кто показал, как моделировать правильные и полуправильные многогранники , очерчивая их рамки на плоскости. Он также различал устойчивые и неустойчивые равновесия. [7]

Стевин внес вклад в тригонометрию своей книгой « De Driehouckhandel» .

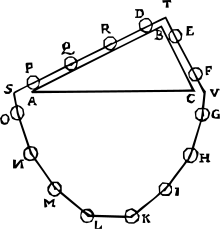
В Первой книге «Начал искусства взвешивания», Вторая часть: О предложениях [Свойства косых тяжестей], Страница 41, Теорема XI, Предложение XIX , [11] он вывел условие для равновесия сил на наклонных плоскостях, используя диаграмму с «венком», содержащим равномерно расположенные круглые массы, покоящиеся на плоскостях треугольной призмы (см. иллюстрацию сбоку). Он пришел к выводу, что требуемые веса пропорциональны длинам сторон, на которых они покоятся, предполагая, что третья сторона горизонтальна, и что эффект веса уменьшается аналогичным образом. Подразумевается, что коэффициент уменьшения равен высоте треугольника, деленной на сторону (синус угла стороны по отношению к горизонтали). Диаграмма доказательства этой концепции известна как «Эпитафия Стевина». Как отметил Э. Дж. Дейкстерхейс , доказательство Стевина равновесия на наклонной плоскости можно упрекнуть в использовании вечного движения для доведения до абсурда . Дейкстерхейс говорит, что Стевин «интуитивно использовал принцип сохранения энергии ... задолго до того, как он был сформулирован явно». [2] : 54 

Он продемонстрировал Пьеру Вариньону разрешение сил , которое ранее не было отмечено, хотя оно является простым следствием закона их сложения. [7]

Стевин открыл гидростатический парадокс , который гласит, что давление в жидкости не зависит от формы сосуда и площади основания, а зависит исключительно от его высоты. [7]

Он также дал меру давления на любую заданную часть стенки сосуда. [7]

Он был первым, кто объяснил приливы и отливы, используя притяжение Луны . [7]

В 1586 году он продемонстрировал , что два объекта разного веса падают с одинаковым ускорением. [12] [13]

Теория музыки

Ван де Шпигелинг дер Сингконст .

Первое упоминание о равномерной темперации, связанной с корнем двенадцатой степени из двух на Западе, появилось в незаконченной рукописи Симона Стевина Van de Spiegheling der singconst (около 1605 г.), опубликованной посмертно триста лет спустя, в 1884 г. [14] Однако из-за недостаточной точности его расчетов многие из полученных им чисел (для длины струны) отличались на одну или две единицы от правильных значений. [15] По-видимому, он был вдохновлен трудами итальянского лютниста и музыкального теоретика Винченцо Галилея (отца Галилео Галилея ), бывшего ученика Джозеффо Царлино .

Бухгалтерия

Двойная бухгалтерия могла быть известна Стевину, поскольку он был клерком в Антверпене в молодые годы, либо на практике, либо через посредство работ итальянских авторов, таких как Лука Пачоли и Джероламо Кардано . Однако Стевин был первым, кто рекомендовал использовать безличные счета в национальном домашнем хозяйстве. Он ввел ее в практику для принца Мориса и рекомендовал ее французскому государственному деятелю Сюлли . [16] [7]

Десятичные дроби

Стевин написал 35-страничную брошюру под названием De Thiende («искусство десятых»), впервые опубликованную на голландском языке в 1585 году и переведенную на французский язык как La Disme . Полное название английского перевода было Десятичная арифметика : обучение тому, как выполнять все вычисления с целыми числами без дробей , с помощью четырех принципов общей арифметики: а именно, сложения , вычитания , умножения и деления . Концепции, упомянутые в брошюре, включали единичные дроби и египетские дроби . Мусульманские математики были первыми, кто использовал десятичные дроби вместо обыкновенных дробей в больших масштабах. Книга Аль-Каши «Ключ к арифметике » была написана в начале 15 века и послужила стимулом для систематического применения десятичных дробей к целым числам и их дробям. [17] [18] Но никто не установил их ежедневное использование до Стевина. Он считал это нововведение настолько значительным, что объявил всеобщее введение десятичных монет, мер и весов всего лишь вопросом времени. [19] [7]

Его обозначения довольно громоздки. Точка, разделяющая целые числа от десятичных дробей, кажется, была изобретением Бартоломея Питиска , в чьих тригонометрических таблицах (1612) она встречается, и была принята Джоном Непером в его логарифмических работах (1614 и 1619). [7]

Стевин напечатал маленькие кружочки вокруг показателей различных степеней одной десятой. То, что Стевин намеревался этими обведенными цифрами обозначать просто показатели, ясно из того факта, что он использовал тот же символ для степеней алгебраических величин. Он не избегал дробных показателей; только отрицательные показатели не появляются в его работе. [7]

Стевин писал и о других научных предметах – например, об оптике, географии, астрономии – и ряд его трудов были переведены на латынь В. Снеллиусом ( Виллебрордом Снеллем ). Существуют два полных издания его работ на французском языке, оба напечатаны в Лейдене, одно в 1608 году, другое в 1634 году. [7]

Математика

Математические произведения , 1634

Стевин написал свою «Арифметику» в 1594 году. Этот труд впервые представил западному миру общее решение квадратного уравнения , первоначально задокументированное почти за тысячу лет до этого Брахмагуптой в Индии.

Согласно Ван дер Вардену , Стевин устранил «классическое ограничение «чисел» целыми числами (Евклид) или рациональными дробями (Диофант)... действительные числа образовывали континуум. Его общее понятие действительного числа было принято, молчаливо или явно, всеми последующими учеными». [20] Недавнее исследование приписывает Стевину большую роль в развитии действительных чисел , чем признавали последователи Вейерштрасса . [21] Стевин доказал теорему о промежуточном значении для многочленов, предвосхитив ее доказательство Коши . Стевин использует процедуру «разделяй и властвуй» , подразделяя интервал на десять равных частей. [22] Десятичные дроби Стевина были вдохновением для работы Исаака Ньютона о бесконечных рядах . [23]

Неологизмы

Стевин считал, что голландский язык отлично подходит для научного письма, и он перевел многие математические термины на голландский. В результате голландский язык является одним из немногих западноевропейских языков, в которых есть много математических терминов, которые не происходят от греческого или латинского. Это включает в себя само название wiskunde (математика).

Его взгляд на важность того, чтобы научный язык был таким же, как язык ремесленника, может быть виден из посвящения его книги De Thiende («The Disme» или «The Tenth»): «Симон Стевин желает звездочетам, землемерам, измерителям ковров, измерителям тел в целом, измерителям монет и торговцам удачи». Далее в той же брошюре он пишет: «[этот текст] учит нас всем вычислениям, которые нужны людям, без использования дробей. Можно свести все операции к сложению, вычитанию, умножению и делению с целыми числами».

Некоторые из придуманных им слов претерпели изменения: «aftrekken» ( вычитать ) и «delen» ( делить ) остались прежними, но со временем «menigvuldigen» превратилось в «vermenigvuldigen» ( умножать , добавленное «ver» подчеркивает тот факт, что это действие). «Vergaderen» ( собирать ) превратилось в «optellen» ( складывать , дословно подсчитывать ).

Другим примером является голландское слово, обозначающее диаметр: «middellijn», буквально: линия, проходящая через середину.

Слово «zomenigmaal» ( quotient , дословно «столько раз») в современном голландском языке было заменено на «quotiënt».

Другие термины не вошли в современный математический голландский язык, например, «teerling» ( die , хотя по-прежнему используется в значении игральная кость), а не «cube».

Интересные факты

Публикации

Укрепления Мёрса , спроектированные Симоном Стевином.

Среди прочего он опубликовал:

Ссылки

  1. ^ Позднее исследователи обнаружили, что десятичные дроби уже были введены средневековым исламским ученым аль-Уклидиси в книге, написанной в 952 году.
  1. ^ ab Cohen, H. Floris (2001). "Stevin, Simon" . Grove Music Online . Оксфорд: Oxford University Press . doi :10.1093/gmo/9781561592630.article.45068. ISBN 978-1-56159-263-0. (требуется подписка или членство в публичной библиотеке Великобритании)
  2. ^ ab EJ Dijksterhuis (1970) Саймон Стевин: Наука в Нидерландах около 1600 года , Гаага: Martinus Nijhoff Publishers , голландский оригинал 1943 года, 's-Gravenhage
  3. ^ (nl) Г. Ван де Берг Het tijdschrift De Vlaamse Stam, jaargang 34, стр. 323–328 и (nl) Библиография к статье Ван Ден Берга в De Vlaamse Stam'
  4. ^ abcd О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (январь 2004 г.), «Саймон Стевин», Архив истории математики MacTutor , Университет Сент-Эндрюс
  5. ^ ab Удивительный мир Саймона Стевина: «Магия — это не магия», Дж. Т. Девриз, Г. Ванден Берге, WIT Press, 1-е изд., 2008 г.
  6. ^ Dijksterhuis EJ (редактор), Основные работы Саймона Стевина, том I, Механика (NV Swets & Zeitlinger, Амстердам, 1955)
  7. ^ abcdefghijklm  Одно или несколько из предыдущих предложений включают текст из публикации, которая сейчас находится в общественном достоянии :  Chisholm, Hugh , ed. (1911). "Stevinus, Simon". Encyclopaedia Britannica (11-е изд.). Cambridge University Press.
  8. ^ Аб Сартон, Джордж (1934). «Симон Стевин Брюгге (1548–1620)». Исида . 21 (2): 241–303. дои : 10.1086/346851. S2CID  144054163.
  9. ^ "Премия Стевина NWO". NWO .
  10. ↑ История науки: сила, доказательство и страсть – Эпизод 4: Можем ли мы обладать неограниченной силой?
  11. ^ Основные труды Симона Стевина
  12. ^ Приложение к De Beghinselen Der Weeghconst
  13. ^ Шиллинг, Говерт (31 июля 2017 г.). Рябь в пространстве-времени: Эйнштейн, гравитационные волны и будущее астрономии. Издательство Гарвардского университета. ISBN 9780674971660.
  14. ^ "Van de spiegheling der singconst". Diapason.xentonic.org. 30 июня 2009 г. Архивировано из оригинала 17 июля 2011 г. Получено 29 декабря 2012 г.
  15. ^ Кристенсен, Томас С. (2006). Кембриджская история западной музыкальной теории , стр. 205, Cambridge University Press. ISBN 9781316025482 . 
  16. ^ Volmer, Frans. «Стевин, Саймон (1548–1620)». В History of Accounting: An International Encyclopedia, под редакцией Майкла Чатфилда и Ричарда Вангермиша. Нью-Йорк: Garland Publishing, 1996, стр. 565–566.
  17. ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (июль 2009 г.), «Аль-Каши», Архив истории математики Мактьютора , Университет Сент-Эндрюс
  18. ^ Флегг, Грэм (2002). Числа: их история и значение . Dover Publications . стр. 75–76. ISBN 9780486421650.
  19. ^ Табак, Джон (2004). Числа: компьютеры, философы и поиск смысла . Факты в архиве . стр. 41–42. ISBN 0-8160-4955-6.
  20. ^ ван дер Варден, BL (1985). История алгебры. От аль-Хорезми до Эмми Нётер . Берлин: Springer-Verlag. п. 69. ИСБН 3-540-13610-X.
  21. ^ Карин Усади Кац и Михаил Г. Кац (2011) Берджессианская критика номиналистических тенденций в современной математике и ее историографии. Основания науки . doi :10.1007/s10699-011-9223-1
  22. ^ Карин Усади Кац и Михаил Г. Кац (2011) Числа Стевина и реальность. Основы науки . doi :10.1007/s10699-011-9228-9 Онлайн впервые. [1]
  23. ^ Блащик, Петр; Кац, Михаил ; Шерри, Дэвид (2012), «Десять заблуждений из истории анализа и их разоблачение», Foundations of Science , 18 : 43–74, arXiv : 1202.4153 , doi : 10.1007/s10699-012-9285-8, S2CID  119134151
  24. ^ simonstevin.tue.nl
  25. ^ Кроун и др., ред. 1955–1966, т. I, стр. 11 [ постоянная мертвая ссылка ]
  26. ^ "RV Simon Stevin. Платформа для морских исследований". Flanders Marine Institute . Получено 11 августа 2022 г.
  27. ^ Тема, содержащаяся в http://www-history.mcs.st-and.ac.uk/Biographies/Stevin.html, соответствующая часть может быть найдена с помощью строки "Wiskonstighe Ghedachtenissen". Краткое изложение можно найти по ссылке
  28. ^ Стевин, Саймон, Les œuvres mathématiques...

Дальнейшее чтение