Бисекция

Деление чего-либо на две равные или конгруэнтные части

Прямая DE делит пополам прямую AB в точке D, прямая EF является серединным перпендикуляром к отрезку AD в точке C, а прямая EF является внутренней биссектрисой прямого угла AED.

В геометрии бисекция — это деление чего-либо на две равные или конгруэнтные части (имеющие одинаковую форму и размер). Обычно это включает в себя биссектрису , также называемую биссектрисой . Наиболее часто рассматриваемыми типами биссектрис являются биссектриса отрезка , прямая , проходящая через середину данного отрезка , и биссектриса угла , прямая, проходящая через вершину угла (которая делит его на два равных угла ). В трехмерном пространстве бисекция обычно выполняется биссектрисой , также называемой биссектрисой .

Перпендикулярный отрезок биссектрисы

Определение

Перпендикуляр к отрезку прямой

• Серединный перпендикуляр отрезка — это прямая, которая пересекает отрезок в его середине перпендикулярно.
• Перпендикуляр к отрезку прямой также обладает тем свойством , что каждая его точка равноудалена от конечных точек отрезка AB: ${\displaystyle AB}$ ${\displaystyle X}$

(Д) . ${\displaystyle \quad |XA|=|XB|}$

Доказательство следует из теоремы Пифагора : ${\displaystyle }$

${\displaystyle |XA|^{2}=|XM|^{2}+|MA|^{2}=|XM|^{2}+|MB|^{2}=|XB|^{2}\;.}$

Свойство (D) обычно используется для построения серединного перпендикуляра:

Построение с помощью линейки и циркуля

Построение с помощью линейки и циркуля

В классической геометрии бисекция — это простое построение с помощью циркуля и линейки , возможность которого зависит от умения рисовать дуги одинакового радиуса и с разными центрами:

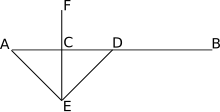
Отрезок делится пополам путем рисования пересекающихся окружностей одинакового радиуса , центры которых являются конечными точками отрезка. Прямая, определяемая точками пересечения двух окружностей, является перпендикуляром к отрезку. Поскольку построение биссектрисы выполняется без знания середины отрезка , построение используется для определения как пересечение биссектрисы и отрезка прямой. ${\displaystyle AB}$ ${\displaystyle r>{\tfrac {1}{2}}|AB|}$
${\displaystyle M}$ ${\displaystyle M}$

Это построение фактически используется при построении линии, перпендикулярной данной прямой в данной точке : проводится окружность, центр которой пересекает прямую в двух точках , а перпендикуляр, который необходимо построить, является биссектором . ${\displaystyle g}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle A,B}$ ${\displaystyle AB}$

Уравнения

Если — радиус-векторы двух точек , то ее середина — а вектор — нормальный вектор перпендикулярного отрезка биссектрисы. Следовательно, ее векторное уравнение — . Подстановка и раскрытие уравнения приводит к векторному уравнению ${\displaystyle {\vec {a}},{\vec {b}}}$ ${\displaystyle A,B}$ ${\displaystyle M:{\vec {m}}={\tfrac {{\vec {a}}+{\vec {b}}}{2}}}$ ${\displaystyle {\vec {a}}-{\vec {b}}}$ ${\displaystyle ({\vec {x}}-{\vec {m}})\cdot ({\vec {a}}-{\vec {b}})=0}$ ${\displaystyle {\vec {m}}=\cdots }$

(В) ${\displaystyle \quad {\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\tfrac {1}{2}}({\vec {a}}^{2}-{\vec {b}}^{2}).}$

При этом получаем уравнение в координатной форме: ${\displaystyle A=(a_{1},a_{2}),B=(b_{1},b_{2})}$

(С) ${\displaystyle \quad (a_{1}-b_{1})x+(a_{2}-b_{2})y={\tfrac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2})\;.}$

Или явно:
(E) , где , , и . ${\displaystyle \quad y=m(x-x_{0})+y_{0}}$
${\displaystyle \;m=-{\tfrac {b_{1}-a_{1}}{b_{2}-a_{2}}}}$ ${\displaystyle \;x_{0}={\tfrac {1}{2}}(a_{1}+b_{1})\;}$ ${\displaystyle \;y_{0}={\tfrac {1}{2}}(a_{2}+b_{2})\;}$

Приложения

Серединные перпендикулярные отрезки использовались при решении различных геометрических задач:

1. Построение центра круга Фалеса ,
2. Построение центра вневписанной окружности треугольника,
3. Границы диаграммы Вороного состоят из отрезков таких линий или плоскостей.

Биссектрисная плоскость

Перпендикулярные биссектрисы отрезков в пространстве

• Серединный перпендикуляр отрезка — это плоскость , которая пересекает отрезок в его середине перпендикулярно.

Его векторное уравнение буквально такое же, как и в случае плоскости:

(В) ${\displaystyle \quad {\vec {x}}\cdot ({\vec {a}}-{\vec {b}})={\tfrac {1}{2}}({\vec {a}}^{2}-{\vec {b}}^{2}).}$

При этом получаем уравнение в координатной форме: ${\displaystyle A=(a_{1},a_{2},a_{3}),B=(b_{1},b_{2},b_{3})}$

(С3) ${\displaystyle \quad (a_{1}-b_{1})x+(a_{2}-b_{2})y+(a_{3}-b_{3})z={\tfrac {1}{2}}(a_{1}^{2}-b_{1}^{2}+a_{2}^{2}-b_{2}^{2}+a_{3}^{2}-b_{3}^{2})\;.}$

Свойство (D) (см. выше) буквально верно и в пространстве:
(D) Перпендикулярная серединная плоскость отрезка обладает для любой точки свойством: . ${\displaystyle AB}$ ${\displaystyle X}$ ${\displaystyle \;|XA|=|XB|}$

Биссектриса угла

Деление угла пополам с помощью циркуля и линейки

Биссектриса угла делит угол на два угла с равными мерами. У угла есть только одна биссектриса. Каждая точка биссектрисы угла равноудалена от сторон угла.

«Внутренняя» или «внутренняя биссектриса» угла — это линия, полупрямая или отрезок, которые делят угол меньше 180° на два равных угла. «Внешняя» или «внешняя биссектриса» — это линия, которая делит дополнительный угол (180° минус исходный угол), образованный одной стороной, образующей исходный угол, и продолжением другой стороны, на два равных угла. ^[1]

Чтобы разделить угол пополам с помощью линейки и циркуля , нужно нарисовать окружность, центр которой является вершиной. Окружность пересекает угол в двух точках: по одной на каждой стороне. Используя каждую из этих точек как центр, нарисуйте две окружности одинакового размера. Пересечение окружностей (две точки) определяет линию, которая является биссектрисой угла.

Доказательство правильности этой конструкции довольно интуитивно, опираясь на симметрию задачи. Трисекция угла (деление его на три равные части) не может быть достигнута только с помощью циркуля и линейки (это было впервые доказано Пьером Ванцелем ).

Внутренняя и внешняя биссектрисы угла перпендикулярны . Если угол образован двумя прямыми, заданными алгебраически как и тогда внутренняя и внешняя биссектрисы задаются двумя уравнениями ^{[2] : стр.15} ${\displaystyle l_{1}x+m_{1}y+n_{1}=0}$ ${\displaystyle l_{2}x+m_{2}y+n_{2}=0,}$

${\displaystyle {\frac {l_{1}x+m_{1}y+n_{1}}{\sqrt {l_{1}^{2}+m_{1}^{2}}}}=\pm {\frac {l_{2}x+m_{2}y+n_{2}}{\sqrt {l_{2}^{2}+m_{2}^{2}}}}.}$

Треугольник

Параллелизмы и коллинеарности

Биссектрисы внутренних углов треугольника пересекаются в точке, называемой центром окружности треугольника, как показано на рисунке.

Биссектрисы двух внешних углов и биссектриса другого внутреннего угла пересекаются в одной точке. ^{[3] : стр.149}

Три точки пересечения, каждая из которых является биссектрисой внешнего угла с противоположной продолженной стороной , являются коллинеарными (лежат на одной прямой друг с другом). ^{[3] : стр. 149}

Три точки пересечения, две из которых находятся между биссектрисой внутреннего угла и противолежащей стороной, а третья — между биссектрисой другого внешнего угла и продолженной противолежащей стороной, лежат на одной прямой. ^{[3] : стр. 149}

Теорема о биссектрисе угла

На этой диаграмме BD:DC = AB:AC.

Теорема о биссектрисе угла касается относительных длин двух отрезков, на которые делится сторона треугольника линией, делящей пополам противолежащий угол. Она приравнивает их относительные длины к относительным длинам двух других сторон треугольника.

Длины

Если длины сторон треугольника равны , полупериметр и А — противолежащая сторона угла , то длина внутренней биссектрисы угла А равна ^{[3] : стр. 70} ${\displaystyle a,b,c}$ ${\displaystyle s=(a+b+c)/2,}$ ${\displaystyle a}$

${\displaystyle {\frac {2{\sqrt {bcs(s-a)}}}{b+c}},}$

или в тригонометрических терминах, ^[4]

${\displaystyle {\frac {2bc}{b+c}}\cos {\frac {A}{2}}.}$

Если внутренняя биссектриса угла A в треугольнике ABC имеет длину и если эта биссектриса делит сторону, противолежащую A, на отрезки длин m и n , то ^{[3] : стр.70} ${\displaystyle t_{a}}$

${\displaystyle t_{a}^{2}+mn=bc}$

где b и c — длины сторон, противоположных вершинам B и C; а сторона, противоположная A, делится в пропорции b : c .

Если внутренние биссектрисы углов A, B и C имеют длины и , то ^[5] ${\displaystyle t_{a},t_{b},}$ ${\displaystyle t_{c}}$

${\displaystyle {\frac {(b+c)^{2}}{bc}}t_{a}^{2}+{\frac {(c+a)^{2}}{ca}}t_{b}^{2}+{\frac {(a+b)^{2}}{ab}}t_{c}^{2}=(a+b+c)^{2}.}$

Никакие два неконгруэнтных треугольника не имеют одинакового набора из трех длин биссектрис внутренних углов. ^{[6] [7]}

Целочисленные треугольники

Существуют целочисленные треугольники с рациональной биссектрисой .

Четырехугольник

Внутренние биссектрисы выпуклого четырехугольника либо образуют вписанный четырехугольник (то есть четыре точки пересечения смежных биссектрис являются концентрическими ), ^[8] либо они являются конкурирующими . В последнем случае четырехугольник является тангенциальным четырехугольником .

Ромб

Каждая диагональ ромба делит пополам его противолежащие углы.

Экс-тангенциальный четырехугольник

Вневписанный центр внеописанного четырехугольника лежит на пересечении шести биссектрис. Это внутренние биссектрисы двух противолежащих углов, внешние биссектрисы (биссектрисы дополнительных углов) двух других углов и внешние биссектрисы углов, образованных при пересечении продолжений противоположных сторон .

Парабола

Касательная к параболе в любой точке делит пополам угол между линией, соединяющей точку с фокусом, и линией, выходящей из точки и перпендикулярной директрисе .

Биссектрисы сторон многоугольника

Треугольник

Медианы

Каждая из трех медиан треугольника представляет собой отрезок прямой, проходящий через одну вершину и середину противоположной стороны, поэтому он делит эту сторону пополам (хотя в общем случае не перпендикулярно). Три медианы пересекаются в точке, которая называется центроидом треугольника , который является его центром масс , если он имеет равномерную плотность; таким образом, любая линия, проходящая через центроид треугольника и одну из его вершин, делит пополам противоположную сторону. Центроид находится в два раза ближе к середине любой стороны, чем к противоположной вершине.

Перпендикулярные серединные перпендикуляры

Внутренний перпендикулярный биссектрисе стороны треугольника — это отрезок, полностью падающий на треугольник и находящийся внутри него, линии, которая перпендикулярно делит эту сторону пополам. Три перпендикулярных биссектрисы трех сторон треугольника пересекаются в центре описанной окружности (центре окружности, проходящей через три вершины). Таким образом, любая линия, проходящая через центр описанной окружности треугольника и перпендикулярная стороне, делит эту сторону пополам.

В остроугольном треугольнике центр описанной окружности делит внутренние перпендикулярные серединные отрезки двух самых коротких сторон в равных пропорциях. В тупоугольном треугольнике перпендикулярные серединные отрезки двух самых коротких сторон (продолженные за пределы их противоположных треугольных сторон к центру описанной окружности) делятся соответствующими им пересекающимися треугольными отрезками в равных пропорциях. ^{[9] : Следствия 5 и 6}

Для любого треугольника внутренние перпендикулярные серединные перпендикуляры определяются как , где стороны равны , а площадь равна ^{[9] : Теория 2} ${\displaystyle p_{a}={\tfrac {2aT}{a^{2}+b^{2}-c^{2}}},}$ ${\displaystyle p_{b}={\tfrac {2bT}{a^{2}+b^{2}-c^{2}}},}$ ${\displaystyle p_{c}={\tfrac {2cT}{a^{2}-b^{2}+c^{2}}},}$ ${\displaystyle a\geq b\geq c}$ ${\displaystyle T.}$

Четырехугольник

Две бимедианы выпуклого четырехугольника — это отрезки прямых, соединяющие середины противоположных сторон, следовательно, каждая из них делит пополам две стороны. Две бимедианы и отрезок прямой, соединяющий середины диагоналей, совпадают в точке, называемой «вершинным центроидом», и все они делятся пополам этой точкой. [ ^{10] : стр.125}

Четыре "малютиды" выпуклого четырехугольника являются перпендикулярами к стороне, проходящей через середину противоположной стороны, следовательно, делящей последнюю сторону пополам. Если четырехугольник вписанный ( вписан в окружность), эти малютиды совпадают (все встречаются) в общей точке, называемой "антицентром".

Теорема Брахмагупты утверждает, что если вписанный четырехугольник является ортодиагональным (то есть имеет перпендикулярные диагонали ), то перпендикуляр к стороне из точки пересечения диагоналей всегда делит пополам противоположную сторону.

Построение перпендикуляра по серединам образует четырехугольник из перпендикуляров по серединам сторон другого четырехугольника.

Биссектрисы площади и биссектрисы периметра

Треугольник

Существует бесконечное множество линий, которые делят площадь треугольника пополам . Три из них являются медианами треугольника (соединяющими середины сторон с противоположными вершинами), и они совпадают в центре тяжести треугольника ; действительно, они являются единственными биссектрисами площади, проходящими через центр тяжести. Три другие биссектрисы площади параллельны сторонам треугольника; каждая из них пересекает две другие стороны так, чтобы разделить их на сегменты с пропорциями . ^[11] Эти шесть линий совпадают по три за раз: в дополнение к тому, что три медианы совпадают, любая медиана совпадает с двумя биссектрисами площади, параллельными сторонам. ${\displaystyle {\sqrt {2}}+1:1}$

Огибающая бесконечности биссектрис площади является дельтоидом (в широком смысле определяемым как фигура с тремя вершинами, соединенными кривыми, вогнутыми к внешней стороне дельтоида, что делает внутренние точки невыпуклым множеством). ^{[11] Вершины дельтоида находятся} в серединах медиан; все точки внутри дельтоида находятся на трех различных биссектрисах площади, в то время как все точки снаружи находятся только на одной. [1] Стороны дельтоида являются дугами гипербол , которые асимптотичны к продолженным сторонам треугольника. ^[11] Отношение площади огибающей биссектрис площади к площади треугольника является инвариантом для всех треугольников и равно, т. е. 0,019860... или менее 2%. ${\displaystyle {\tfrac {3}{4}}\log _{e}(2)-{\tfrac {1}{2}},}$

Скалывающий треугольник — это отрезок прямой, который делит периметр треугольника пополам и имеет одну конечную точку в середине одной из трех сторон. Три скалывающих треугольника сходятся в (все проходят через) центр окружности Шпикера , которая является вписанной окружностью срединного треугольника . Скалывающие треугольники параллельны биссектрисам угла.

Разделитель треугольника — это отрезок прямой, имеющий одну конечную точку в одной из трех вершин треугольника и делящий периметр пополам. Три разделителя сходятся в точке Нагеля треугольника.

Любая линия, проходящая через треугольник, которая делит пополам и площадь треугольника, и его периметр, проходит через инцентр треугольника (центр его вписанной окружности ). Для любого данного треугольника их может быть один, два или три. Линия, проходящая через инцентр, делит пополам одну из площади или периметра тогда и только тогда, когда она также делит пополам другую. ^[12]

Параллелограмм

Любая линия, проходящая через середину параллелограмма , делит его площадь ^[11] и периметр пополам.

Круг и эллипс

Все биссектрисы площади и периметра круга или другого эллипса проходят через центр , и любые хорды, проходящие через центр, делят площадь и периметр пополам. В случае круга они являются диаметрами круга .

Биссектрисы диагоналей

Параллелограмм

Диагонали параллелограмма точкой пересечения делятся пополам .

Четырехугольник

Если отрезок прямой, соединяющий диагонали четырехугольника, делит обе его диагонали пополам, то этот отрезок прямой ( линия Ньютона ) сам делится пополам центром тяжести вершины.

Биссектрисы объема

Плоскость, которая делит два противоположных ребра тетраэдра в заданном отношении, также делит объем тетраэдра в том же отношении. Таким образом, любая плоскость, содержащая бимедиану (соединитель середин противоположных ребер) тетраэдра, делит объем тетраэдра пополам ^{[13] [14] : стр.89–90}

Ссылки

1. Вайсштейн, Эрик В. «Биссектриса внешнего угла». Из MathWorld — веб-ресурса Wolfram.
2. Спейн, Барри. Аналитические конические сечения , Dover Publications, 2007 (ориг. 1957).
3. Джонсон, Роджер А., Advanced Euclidean Geometry , Dover Publ., 2007 (ориг. 1929).
4. Оксман, Виктор. «О существовании треугольников с заданными длинами одной стороны и двумя смежными биссектрисами», Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
5. Саймонс, Стюарт. Mathematical Gazette 93, март 2009 г., 115-116.
6. Миронеску, П. и Панаитопол, Л., «Существование треугольника с заданными длинами биссектрис», American Mathematical Monthly 101 (1994): 58–60.
7. Оксман, Виктор, «Чисто геометрическое доказательство единственности треугольника с предписанными биссектрисами», Forum Geometricorum 8 (2008): 197–200.
8. Weisstein, Eric W. "Четырехугольник". Из MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Quadrilateral.html
9. Митчелл, Дуглас В. (2013), «Перпендикулярные серединные перпендикуляры сторон треугольника», Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
10. Альтшиллер-Корт, Натан, College Geometry , Dover Publ., 2007.
11. Dunn, Jas. A.; Pretty, Jas. E. (май 1972). «Деление треугольника пополам». The Mathematical Gazette . 56 (396): 105–108. doi :10.2307/3615256. JSTOR  3615256.
12. Кодокостас, Димитриос, «Уравнители треугольников», Mathematics Magazine 83, апрель 2010 г., стр. 141-146.
13. Weisstein, Eric W. "Tetrahedron." Из MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Tetrahedron.html
14. Альтшиллер-Корт, Н. «Тетраэдр». Гл. 4 в Modern Pure Solid Geometry : Chelsea, 1979.

Внешние ссылки

• Биссектриса угла в разрезе узла
• Определение биссектрисы угла. Математика Открыть справочник С интерактивным апплетом
• Определение биссектрисы линии. Математика Открыть справочник С интерактивным апплетом
• Перпендикулярная биссектриса. С интерактивным апплетом
• Анимированные инструкции по делению угла и линии пополам с помощью циркуля и линейки
• Вайсштейн, Эрик В. "Биссектриса прямой". MathWorld .

В данной статье использованы материалы из Angle bisector на PlanetMath , которые лицензированы в соответствии с лицензией Creative Commons Attribution/Share-Alike License .