В математике специальная ортогональная группа в трех измерениях, также известная как группа вращения SO(3) , является естественным примером многообразия . Различные диаграммы SO(3) устанавливают конкурирующие системы координат : в этом случае нельзя сказать, что существует предпочтительный набор параметров , описывающих вращение. Имеется три степени свободы , так что размерность SO(3) равна трем. Во многих приложениях используется та или иная система координат, и возникает вопрос, как перейти из одной системы в другую.
В геометрии группа вращений — это группа всех вращений вокруг начала координат трехмерного евклидова пространства R 3 под действием операции композиции . [1] По определению, вращение вокруг начала координат — это линейное преобразование , которое сохраняет длину векторов (это изометрия ) и сохраняет ориентацию (т. е. направленность ) пространства. Преобразование, сохраняющее длину и меняющее ориентацию, называется неправильным вращением . Каждое неправильное вращение трехмерного евклидова пространства — это вращение, за которым следует отражение в плоскости, проходящей через начало координат.
Составление двух вращений приводит к созданию еще одного вращения; каждое вращение имеет уникальное обратное вращение; и тождественная карта удовлетворяет определению вращения. Благодаря указанным выше свойствам совокупность всех вращений представляет собой составную группу . Более того, группа вращений имеет естественную структуру многообразия , для которой групповые операции гладкие ; так что на самом деле это группа Ли . Группу ротации часто обозначают SO(3) по причинам, объясненным ниже.
Пространство вращений изоморфно множеству операторов вращения и множеству ортонормированных матриц с определителем +1. Он также тесно связан ( двойное покрытие ) с набором кватернионов с их внутренним произведением, а также с набором векторов вращения (хотя здесь связь сложнее описать, подробности см. ниже), с другой внутренней операцией композиции. заданы произведением их эквивалентных матриц.
Обозначения векторов вращения возникают из теоремы Эйлера о вращении , которая утверждает, что любое вращение в трех измерениях можно описать поворотом на некоторый угол вокруг некоторой оси. Учитывая это, мы можем затем указать ось одного из этих поворотов на два угла и использовать радиус вектора для указания угла поворота . Эти векторы представляют собой трехмерный шар с необычной топологией.
Эта трехмерная твердая сфера эквивалентна поверхности четырехмерного диска, который также является трехмерной разновидностью. Для выполнения этой эквивалентности нам нужно будет определить, как мы будем представлять вращение с помощью этой встроенной в 4D поверхности.
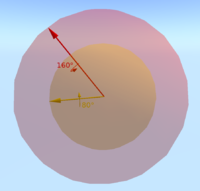
Интересно рассматривать пространство как трехмерную сферу S 3 , границу диска в 4-мерном евклидовом пространстве. Для этого нам нужно будет определить, как мы будем представлять вращение с помощью этой встроенной в 4D поверхности.
Способ использования радиуса для указания угла поворота не является простым. Это может быть связано с кругами широты в сфере с определенным северным полюсом и объясняется следующим образом:
Начиная с северного полюса сферы в трехмерном пространстве, мы указываем точку на северном полюсе, которая представляет тождественное вращение. В случае индивидуального вращения ось вращения не определена, а угол поворота (нулевой) не имеет значения. Вращение, ось которого находится в плоскости xy , и с очень малым углом поворота, можно задать срезом сферы, параллельным плоскости xy и очень близко к северному полюсу. Круг, определяемый этим срезом, будет очень маленьким, что соответствует небольшому углу поворота. По мере того, как углы поворота становятся больше, срез перемещается на юг, а круги становятся больше, пока не будет достигнут экватор сферы, что будет соответствовать углу поворота 180 градусов. Продолжая двигаться на юг, радиусы кругов теперь становятся меньше (что соответствует абсолютному значению угла поворота, рассматриваемому как отрицательное число). Наконец, когда достигается южный полюс, круги снова сжимаются до единичного вращения, которое также указывается как точка на южном полюсе. Обратите внимание, что с помощью этой визуализации можно увидеть ряд характеристик таких вращений и их представлений.
Пространство вращений непрерывно, каждое вращение имеет окрестность вращений, которые почти одинаковы, и эта окрестность становится плоской по мере сжатия окрестности.

Кроме того, каждое вращение фактически представлено двумя противоположными точками на сфере, которые находятся на противоположных концах линии, проходящей через центр сферы. Это отражает тот факт, что каждое вращение можно представить как вращение вокруг некоторой оси или, что то же самое, как отрицательное вращение вокруг оси, направленной в противоположную сторону (так называемое двойное покрытие ). «Широта» круга, представляющего определенный угол вращения, будет равна половине угла, представленного этим вращением, поскольку при перемещении точки с северного полюса на южный широта колеблется от нуля до 180 градусов, а угол вращения варьируется от 0 до 360 градусов . («Долгота» точки тогда представляет собой конкретную ось вращения.) Однако обратите внимание, что этот набор вращений не замкнут при композиции.
Два последовательных вращения с осями в плоскости xy не обязательно дадут вращение, ось которого лежит в плоскости xy , и поэтому не может быть представлена как точка на сфере. Этого не произойдет с общим вращением в трехмерном пространстве, которое образует замкнутое множество при композиции.
Эту визуализацию можно расширить до общего вращения в трехмерном пространстве. Тождественное вращение представляет собой точку, а небольшой угол поворота вокруг некоторой оси можно представить как точку на сфере малого радиуса. По мере увеличения угла поворота сфера увеличивается, пока угол поворота не достигнет 180 градусов, после чего сфера начинает сжиматься, становясь точкой, когда угол приближается к 360 градусам (или нулю градусов от отрицательного направления). Этот набор расширяющихся и сжимающихся сфер представляет собой гиперсферу в четырехмерном пространстве (3-сферу).
Как и в более простом примере выше, каждому вращению, представленному как точка на гиперсфере, соответствует противоположная точка на этой гиперсфере. «Широта» гиперсферы будет равна половине соответствующего угла поворота, и окрестность любой точки станет «более плоской» (т.е. будет представлена трехмерным евклидовым пространством точек) по мере сжатия окрестностей.
Этому поведению соответствует набор единичных кватернионов : общий кватернион представляет точку в четырехмерном пространстве, но ограничение его единичной величины дает трехмерное пространство, эквивалентное поверхности гиперсферы. Величина единичного кватерниона будет равна единице, что соответствует гиперсфере единичного радиуса.
Векторная часть единичного кватерниона представляет собой радиус 2-сферы, соответствующей оси вращения, а ее величина равна синусу половины угла поворота. Каждое вращение представлено двумя единичными кватернионами противоположного знака, и, как и в пространстве вращений в трех измерениях, кватернионное произведение двух единичных кватернионов даст единичный кватернион. Кроме того, пространство единичных кватернионов «плоское» в любой бесконечно малой окрестности данного единичного кватерниона.
Мы можем параметризовать пространство вращений несколькими способами, но вырождения будут возникать всегда. Например, если мы используем три угла ( углы Эйлера ), такая параметризация вырождается в некоторых точках гиперсферы, что приводит к проблеме блокировки карданного подвеса . Мы можем избежать этого, используя четыре евклидовых координаты w , x , y , z , где w 2 + x 2 + y 2 + z 2 = 1. Точка ( w , x , y , z ) представляет собой вращение вокруг оси, направленной вектором ( x , y , z ) на угол
Эта проблема аналогична параметризации двумерной поверхности сферы двумя координатами, такими как широта и долгота. Широта и долгота плохо ведут себя ( вырождаются ) на северном и южном полюсах, хотя полюса по своей сути не отличаются от любых других точек сферы. На полюсах (широты +90° и −90°) долгота теряет смысл. Можно показать, что ни одна двухпараметрическая система координат не может избежать такого вырождения.
Возможные кандидаты на параметризацию включают в себя:
Есть проблемы с их использованием в качестве чего-то большего, чем просто локальные карты, из-за их многозначной природы и особенностей. То есть надо быть осторожным прежде всего и работать только с диффеоморфизмами в определении диаграммы . Проблемы такого рода неизбежны, поскольку SO(3) диффеоморфно реальному проективному пространству P 3 ( R ), которое является фактором S 3 путем идентификации противоположных точек, а карты пытаются моделировать многообразие с использованием R 3 .
Это объясняет, почему, например, углы Эйлера дают переменную в 3- торе , а единичные кватернионы в 3-сфере . Единственность представления углами Эйлера нарушается в некоторых точках (см. карданный замок ), в то время как представление кватернионов всегда представляет собой двойное покрытие , где q и − q дают одно и то же вращение.
Если мы используем кососимметричную матрицу, каждая кососимметричная матрица 3 × 3 определяется тремя параметрами, и поэтому на первый взгляд пространство параметров равно R 3 . Возведение такой матрицы в степень приводит к ортогональной матрице 3 × 3 с определителем 1 – другими словами, матрице вращения, но это отображение «многие к одному». Обратите внимание, что это не покрывающее отображение — хотя это локальный гомеоморфизм вблизи начала координат, оно не является покрывающим при повороте на 180 градусов. Можно ограничить эти матрицы шаром вокруг начала координат в R 3 так, чтобы повороты не превышали 180 градусов, и это будет взаимно однозначно, за исключением поворотов на 180 градусов, которые соответствуют границе S 2 , и они определяют противоположные точки – это локус разреза . 3-шар с такой идентификацией границы — это P 3 ( R ). Аналогичная ситуация справедлива и для применения преобразования Кэли к кососимметричной матрице.
Угол оси дает параметры в S 2 × S 1 ; если мы заменим единичный вектор фактической осью вращения, так что n и − n дают одну и ту же осевую линию, набор осей станет P 2 ( R ), реальной проективной плоскостью . Но поскольку вращения вокруг n и − n параметризуются противоположными значениями θ, результатом является расслоение S 1 над P 2 ( R ), которое оказывается P 3 ( R ).
Дробно-линейные преобразования используют четыре комплексных параметра: a , b , c и d , с условием, что ad − bc не равно нулю. Поскольку умножение всех четырех параметров на одно и то же комплексное число не меняет параметр, мы можем настаивать на том, что ad − bc =1. Это предполагает запись ( a , b , c , d ) как комплексную матрицу 2 × 2 с определителем 1, то есть как элемент специальной линейной группы SL(2, C ). Но не все такие матрицы производят вращения: включены также конформные отображения на S2 . Чтобы получить только вращения, мы настаиваем на том, что d — комплексно-сопряженное число a , а c — отрицательное значение комплексно-сопряженного числа b . Тогда у нас есть два комплексных числа, a и b , с учетом | а | 2 +| б | 2 =1. Если мы напишем a + bj , это кватернион единичной длины.
В конечном счете, поскольку R 3 не является P 3 ( R ), с каждым из этих подходов возникнет проблема. В некоторых случаях нам нужно помнить, что определенные значения параметров приводят к одному и тому же вращению, и чтобы устранить эту проблему, необходимо установить границы, но тогда путь через эту область в R 3 должен внезапно перейти в другую область, когда он пересекает границу. Блокировка карданного подвеса представляет собой проблему, когда производная карты не имеет полного ранга, что происходит с углами Эйлера и углами Тейта – Брайана, но не для других вариантов. Представление кватернионов не имеет ни одной из этих проблем (всегда является отображением два к одному), но оно имеет 4 параметра с условием (единичная длина), что иногда затрудняет просмотр трех доступных степеней свободы.
Одной из областей, в которой эти соображения в той или иной форме становятся неизбежными, является кинематика твердого тела . В качестве определения можно принять идею кривой в евклидовой группе E (3) трёхмерного евклидова пространства , начиная с единицы (начального положения). Подгруппа трансляции T группы E (3) является нормальной подгруппой с фактором SO(3), если мы рассматриваем только подгруппу E + (3) прямых изометрий (что разумно с точки зрения кинематики). Поступательную часть можно отделить от вращательной части в стандартной ньютоновской кинематике, рассматривая движение центра масс и вращение твердого тела вокруг центра масс. Следовательно, любое движение твердого тела приводит непосредственно к SO(3), если исключить поступательную часть.
Эти идентификации показывают, что SO(3) связан , но не просто связан . Что касается последнего, то в шаре с выявленными противоположными точками поверхности рассмотрим путь, идущий от «северного полюса» прямо через центр вниз к южному полюсу. Это замкнутый цикл, поскольку северный и южный полюсы идентифицированы. Эту петлю нельзя сжать до точки, поскольку как бы вы ни деформировали петлю, начальная и конечная точка должны оставаться противоположными, иначе петля «разорвется». С точки зрения вращений, эта петля представляет собой непрерывную последовательность вращений вокруг оси z , начинающуюся и заканчивающуюся единичным вращением (т.е. серию поворотов на угол φ, где φ изменяется от 0 до 2π).
Удивительно, но если вы пройдете путь дважды, то есть от северного полюса вниз к южному полюсу и обратно к северному полюсу, так что φ изменяется от 0 до 4π, вы получите замкнутый цикл, который можно сжать до одной точки: первый ход пути непрерывно ведут к поверхности шара, по-прежнему дважды соединяя северный полюс с южным полюсом. Затем вторую половину пути можно отразить на противоположную сторону, вообще не меняя путь. Теперь у нас есть обычная замкнутая петля на поверхности шара, соединяющая северный полюс сам с собой по большому кругу. Этот круг без проблем можно сжать до северного полюса. Фокус с балийской тарелкой и подобные трюки демонстрируют это на практике.
Тот же аргумент можно привести в целом, и он показывает, что фундаментальная группа SO (3) является циклической группой порядка 2. В физических приложениях нетривиальность фундаментальной группы допускает существование объектов, известных как спиноры , и является важным инструментом в разработке теоремы спин-статистики .
Универсальным накрытием SO(3) является группа Ли под названием Spin(3) . Группа Spin(3) изоморфна специальной унитарной группе SU(2); он также диффеоморфен единичной 3-сфере S 3 и может пониматься как группа единичных кватернионов (т.е. кватернионов с абсолютным значением 1). Связь между кватернионами и вращениями, обычно используемая в компьютерной графике , объясняется в кватернионах и пространственных вращениях . Отображение S 3 на SO(3), которое идентифицирует антиподальные точки S 3 , является сюръективным гомоморфизмом групп Ли с ядром {±1}. Топологически это отображение является покрывающим отображением два к одному .