Ведьма из Аньези

В математике ведьма Аньези ( итальянское произношение: [aɲˈɲeːzi, -eːsi; -ɛːzi] ) представляет собой кубическую плоскую кривую, определяемую двумя диаметрально противоположными точками окружности.

Кривая была изучена еще в 1653 году Пьером Ферма , в 1703 году Гвидо Гранди и Исааком Ньютоном . Он получил свое название от итальянского математика Марии Гаэтаны Аньези , опубликовавшей его в 1748 году. Итальянское название la versiera di Agnesi основано на латинском versoria ( лист парусных кораблей) и синусоиде против . Это было прочитано Джоном Колсоном как l'avversiera di Agnesi , где avversiera переводится как «женщина, которая против Бога» и интерпретируется как «ведьма». ^[1]^[2]^[3]^[4]

График производной функции арктангенса представляет собой пример ведьмы Аньези. Как функция плотности вероятности распределения Коши , ведьма Аньези имеет применение в теории вероятностей . Это также приводит к явлению Рунге при приближении функций полиномами , используется для аппроксимации распределения энергии спектральных линий и моделирования формы холмов.

Ведьма касается своей определяющей окружности в одной из двух определяющих точек и асимптотична касательной к окружности в другой точке. Он имеет уникальную вершину (точку крайней кривизны) в точке касания с определяющей окружностью, которая также является соприкасающейся окружностью в этой точке. Он также имеет две конечные точки перегиба и одну бесконечную точку перегиба. Площадь между ведьмой и ее асимптотической линией в четыре раза превышает площадь определяющего круга, а объем вращения кривой вокруг ее определяющей линии в два раза превышает объем тора вращения ее определяющего круга.

Строительство

Анимация, показывающая постройку ведьмы Аньези.

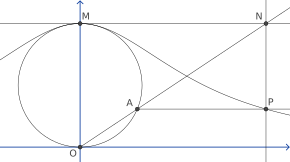
Чтобы построить эту кривую, начните с любых двух точек O и M и нарисуйте круг с диаметром OM . Для любой другой точки A на окружности пусть N будет точкой пересечения секущей линии OA и касательной в точке M. Пусть P — точка пересечения линии, перпендикулярной OM , проходящей через A , и линии, параллельной OM , проходящей через N. Тогда П лежит на ведьме Аньези. Ведьма состоит из всех точек P , которые можно построить таким образом из одного и того же выбора O и M. ^[5] В предельном случае оно включает в себя саму точку М.

Уравнения

Предположим, что точка O находится в начале координат , а точка M лежит на положительной -оси и что окружность диаметром OM имеет радиус . Тогда ведьма, построенная из O и M, имеет декартово уравнение ^[6]^[7] Это уравнение можно упростить, выбрав , до формы или, что то же самое, очистив знаменатели , как кубическое алгебраическое уравнение . В упрощенной форме эта кривая равна график производной арктангенса . ^[8] $y$ $а$ $y={\frac {8a^{3}}{x^{2}+4a^{2}}}.$ $a={\tfrac {1}{2}}$ $y={\frac {1}{x^{2}+1}}.$ $(x^{2}+1)y=1.$

Ведьму Аньези также можно описать параметрическими уравнениями , параметром которых $θ$ является угол между OM и OA , измеренный по часовой стрелке: ^[6]^[7] ${\begin{aligned}x&=2a\tan \theta,\\y&=2a\cos ^{2}\theta.\end{aligned}}$

Характеристики

Основные свойства этой кривой можно вывести из интегрального исчисления . Площадь между ведьмой и ее асимптотической линией в четыре раза превышает площадь фиксированного круга . ^[6]^[7]^[9] Объем обращения ведьмы Аньези вокруг ее асимптоты равен . ^[6] Это в два раза больше объема тора, образованного вращением определяющего круга ведьмы вокруг той же линии. ^[9] $4\pi a^{2}$ $4\pi ^{2}a^{3}$

Кривая имеет единственную вершину в точке касания с определяющей окружностью. То есть эта точка является единственной точкой, где кривизна достигает локального минимума или локального максимума. ^[10] Определяющим кругом ведьмы является также ее соприкасающийся круг в вершине, ^[11] уникальный круг, который «целует» кривую в этой точке, имея одну и ту же ориентацию и кривизну. ^[12] Поскольку это соприкасающийся круг в вершине кривой, он имеет контакт третьего порядка с кривой. ^[13]

Кривая имеет две точки перегиба , в точках, соответствующих углам . ^[6]^[7] Если рассматривать кривую на проективной плоскости, то существует также третья бесконечная точка перегиба, в точке, где линия на бесконечности пересекается асимптотической линией. Поскольку одна из ее точек перегиба бесконечна, у ведьмы есть минимально возможное количество конечных действительных точек перегиба любой неособой кубической кривой. ^[14] $\left(\pm {\frac {2a}{\sqrt {3}}}, {\frac {3a}{2}}\right)$ $\theta =\pm \pi /6$

Наибольшая площадь прямоугольника , который можно вписать между ведьмой и ее асимптотой , равна $4a^{2}$ ^[9]

История

Ранние исследования

Кривая была изучена Пьером де Ферма в его трактате о квадратуре 1659 года . В ней Ферма вычисляет площадь под кривой и (без подробностей) утверждает, что тот же метод распространяется и на циссоиду Диокла . Ферма пишет, что эта кривая была подсказана ему « ab erudito geometra » [ученым геометром]. ^[16] Паради, Пла и Виадер (2008) предполагают, что геометром, который предложил Ферма эту кривую, мог быть Антуан де Лалубер . ^[17]

Приведенную выше конструкцию этой кривой нашел Гранди (1718); такая же конструкция была найдена ранее Исааком Ньютоном , но опубликована только посмертно позже, в 1779 году. ^[18] Гранди (1718) также предложил название versiera (на итальянском языке) или versoria (на латыни) для кривой. ^[19] Латинский термин также используется для обозначения листа , веревки, которая вращает парус, но вместо этого Гранди, возможно, имел в виду просто ссылку на функцию стиха , которая появилась в его конструкции. ^[9]^[18]^[20]^[21]

В 1748 году Мария Гаэтана Аньези опубликовала Instituzioni analitiche ad uso della gioventù italiana , ранний учебник по математическому анализу . ^[15] В него, после первого рассмотрения двух других кривых, она включает исследование этой кривой. Она определяет кривую геометрически как геометрическое место точек, удовлетворяющих определенной пропорции, определяет ее алгебраическое уравнение, находит ее вершину, асимптотическую линию и точки перегиба. ^[22]

Этимология

Мария Гаэтана Аньези назвала кривую по Гранди, versiera . ^[20]^[22] По совпадению, в то время в Италии было принято говорить о Дьяволе другими словами, такими как aversiero или versiero , происходящими от латинского adversarius , «противника» Бога. Версьера , в частности, использовалась для обозначения жены дьявола или «ведьмы». ^[23] Из-за этого профессор Кембриджа Джон Колсон неправильно перевел название кривой как «ведьма». ^[24] Различные современные работы об Аньези и о кривой предполагают несколько разные догадки, как именно произошел этот неправильный перевод. ^[25]^[26] Стройк упоминает, что: ^[22]

Слово [ versiera ] происходит от латинского vertere — поворачивать, но также является аббревиатурой итальянского avversiera — женщины-дьяволицы. Некоторые остроумцы в Англии однажды перевели это слово как «ведьма», и этот глупый каламбур до сих пор бережно сохраняется в большинстве наших учебников на английском языке. ... Кривая уже появлялась в трудах Ферма ( Oeuvres , I, 279–280; III, 233–234) и других; название versiera происходит от Гвидо Гранди ( Quadratura circuli et Hyperbolae , Пиза, 1703). Кривая относится к типу 63 по классификации Ньютона . ... Первым, кто использовал термин «ведьма» в этом смысле, возможно, был Б. Уильямсон, Интегральное исчисление , 7 (1875), 173; ^[27] см. Оксфордский словарь английского языка .

С другой стороны, Стивен Стиглер предполагает, что сам Гранди «возможно, играл словами», двойной каламбур, связывающий дьявола со стихом и функцию синуса с формой женской груди (оба из которых можно записать как «сено» по-итальянски). ^[18]

Приложения

Масштабированная версия кривой представляет собой функцию плотности вероятности распределения Коши . Это распределение вероятностей случайной величины , определенное в результате следующего случайного эксперимента : для фиксированной точки над -осью равномерно случайным образом выберите линию, проходящую через , и пусть будет координатой точки, в которой эта случайная линия пересекает ось. Распределение Коши имеет пиковое распределение, визуально напоминающее нормальное распределение , но его тяжелые хвосты не позволяют ему иметь ожидаемое значение по обычным определениям, несмотря на его симметрию. С точки зрения самой ведьмы это означает, что -координата центроида области между кривой и ее асимптотической линией не определена четко, несмотря на симметрию этой области и конечную площадь. ^[18]^[28] $х$ ${\ displaystyle p}$ $х$ ${\ displaystyle p}$ $х$ $х$

В численном анализе при аппроксимации функций с использованием полиномиальной интерполяции с равноотстоящими друг от друга точками интерполяции для некоторых функций может случиться так, что использование большего количества точек создает худшие аппроксимации, так что интерполяция расходится от функции, которую она пытается аппроксимировать, а не сходится к ней. . Это парадоксальное поведение называется феноменом Рунге . Впервые он был обнаружен Карлом Дэвидом Толме Рунге для функции Рунге , еще одной масштабированной версии ведьмы Аньези, при интерполяции этой функции на интервале . То же самое явление происходит и с самой ведьмой в более широком интервале . ^[29] $y=1/(1+25x^{2})$ $[-1,1]$ $y=1/(1+x^{2})$ $[-5,5]$

Ведьма Аньези аппроксимирует спектральное распределение энергии спектральных линий , особенно рентгеновских линий. ^[30]

Поперечное сечение гладкого холма имеет форму, похожую на Ведьмину. ^[31] Кривые такой формы использовались в качестве типичного топографического препятствия в потоке при математическом моделировании. ^[32]^[33]Одинокие волны на глубокой воде также могут принимать такую форму. ^[34]^[35]

Версия этой кривой была использована Готфридом Вильгельмом Лейбницем для вывода формулы Лейбница для $π$ . Эта формула, бесконечный ряд, может быть получена путем приравнивания площади под кривой к интегралу функции , используя разложение этой функции в ряд Тейлора как бесконечный геометрический ряд и интегрируя почленно. ^[7] ${\frac {\pi }{4}}=1\,-\,{\frac {1}{3}}\,+\,{\frac {1}{5}}\,-\ ,{\frac {1}{7}}\,+\,{\frac {1}{9}}\,-\,\cdots ,$ $1/(1+x^{2})$ $1-x^{2}+x^{4}-x^{6}+\cdots$

В популярной культуре

«Ведьма из Аньези» — название романа Роберта Спиллера. Он включает в себя сцену, в которой учитель излагает версию истории этого термина. ^[36]

Ведьма Аньези — это также название музыкального альбома джазового квартета Radius. На обложке альбома изображено построение ведьмы. ^[37]

Внешние ссылки

В Wikisource есть текст статьи Британской энциклопедии 1911 года « Ведьма Аньези ».

Викискладе есть медиафайлы, связанные с ведьмой Аньези .

«Ведьма Аньези» в Индексе знаменитых кривых MacTutor
Вайсштейн, Эрик В. , «Ведьма Аньези», MathWorld
«Ведьма Аньези» Криса Баучера на основе работы Эрика В. Вайсстейна « Демонстрационный проект Вольфрама» .
«Ведьма Аньези» на «mathcurve»
Лэмб, Эвелин (28 мая 2018 г.), «Несколько моих любимых мест: Ведьма Аньези», Roots of Unity , Scientific American