Волатильность (финансы)

Степень изменения ряда торговых цен с течением времени

Индекс волатильности CBOE (VIX) с декабря 1985 г. по май 2012 г. (ежедневные закрытия)

В финансах волатильность (обычно обозначается как « σ ») — это степень изменения ряда торговых цен с течением времени, обычно измеряемая стандартным отклонением логарифмической доходности .

Историческая волатильность измеряет временной ряд прошлых рыночных цен. Подразумеваемая волатильность смотрит вперед во времени, будучи выведенной из рыночной цены рыночного дериватива (в частности, опциона).

Терминология волатильности

Описанная здесь волатильность относится к фактической волатильности , а именно:

• фактическая текущая волатильность финансового инструмента за определенный период (например, 30 дней или 90 дней), основанная на исторических ценах за определенный период, при этом последним наблюдением является самая последняя цена.
• фактическая историческая волатильность , которая относится к волатильности финансового инструмента за определенный период, но с последним наблюдением на дату в прошлом
  • Почти синонимом является реализованная волатильность , квадратный корень из реализованной дисперсии , в свою очередь рассчитываемый с использованием суммы квадратов доходностей, деленной на количество наблюдений.
• фактическая будущая волатильность , которая относится к волатильности финансового инструмента в течение определенного периода, начинающегося в текущий момент и заканчивающегося в будущем (обычно в дату истечения срока опциона )

Теперь переходим к подразумеваемой волатильности :

• историческая подразумеваемая волатильность , которая относится к подразумеваемой волатильности, наблюдаемой на основе исторических цен финансового инструмента (обычно опционов)
• текущая подразумеваемая волатильность , которая относится к подразумеваемой волатильности, наблюдаемой из текущих цен финансового инструмента
• будущая подразумеваемая волатильность , которая относится к подразумеваемой волатильности, наблюдаемой из будущих цен финансового инструмента

Для финансового инструмента, цена которого следует гауссовскому случайному блужданию или винеровскому процессу , ширина распределения увеличивается с увеличением времени. Это происходит потому, что увеличивается вероятность того, что цена инструмента будет дальше от начальной цены с увеличением времени. Однако, вместо того, чтобы увеличиваться линейно, волатильность увеличивается с квадратным корнем времени с увеличением времени, поскольку ожидается, что некоторые колебания будут компенсировать друг друга, поэтому наиболее вероятное отклонение после удвоения времени не будет вдвое больше расстояния от нуля.

Поскольку наблюдаемые изменения цен не следуют гауссовым распределениям, часто используются другие распределения, такие как распределение Леви . ^[1] Они могут охватывать такие атрибуты, как « толстые хвосты ». Волатильность — это статистическая мера дисперсии вокруг среднего значения любой случайной величины, такой как рыночные параметры и т. д.

Математическое определение

Для любого фонда, который изменяется случайным образом с течением времени, волатильность определяется как стандартное отклонение последовательности случайных величин, каждая из которых представляет собой доходность фонда за некоторую соответствующую последовательность (равных по размеру) времен.

Таким образом, «годовая» волатильность σ _{ежегодно представляет собой стандартное отклонение годовой} логарифмической доходности инструмента . ^[2]

Обобщенная волатильность σ _T для временного горизонта T в годах выражается как:

${\displaystyle \sigma _{\text{T}}=\sigma _{\text{annually}}{\sqrt {T}}.}$

Таким образом, если ежедневная логарифмическая доходность акций имеет стандартное отклонение σ _daily , а период времени доходности равен P в торговых днях, то годовая волатильность равна

${\displaystyle \sigma _{\text{annually}}=\sigma _{\text{daily}}{\sqrt {P}}.}$

так

${\displaystyle \sigma _{\text{T}}=\sigma _{\text{daily}}{\sqrt {PT}}.}$

Обычно предполагается, что P = 252 торговых дня в любом данном году. Тогда, если σ _daily = 0,01, годовая волатильность составляет

${\displaystyle \sigma _{\text{annually}}=0.01{\sqrt {252}}=0.1587.}$

Ежемесячная волатильность (т.е. годовая) составляет ${\displaystyle T={\tfrac {1}{12}}}$

${\displaystyle \sigma _{\text{monthly}}=0.01{\sqrt {\tfrac {252}{12}}}=0.0458.}$

Формулы, использованные выше для преобразования доходностей или показателей волатильности из одного периода времени в другой, предполагают определенную базовую модель или процесс. Эти формулы являются точными экстраполяциями случайного блуждания или процесса Винера, шаги которого имеют конечную дисперсию. Однако, в более общем смысле, для естественных стохастических процессов точное соотношение между показателями волатильности для разных периодов времени более сложное. Некоторые используют показатель устойчивости Леви α для экстраполяции естественных процессов:

${\displaystyle \sigma _{T}=T^{1/\alpha }\sigma .\,}$

Если α  = 2, то получается соотношение масштабирования процесса Винера , но некоторые люди считают, что α  < 2 для финансовой деятельности, такой как акции, индексы и т. д. Это было обнаружено Бенуа Мандельбротом , который изучил цены на хлопок и обнаружил, что они следуют альфа-устойчивому распределению Леви с α  = 1,7. (См. New Scientist, 19 апреля 1997 г.)

Происхождение волатильности

Много исследований было посвящено моделированию и прогнозированию волатильности финансовых доходов, и все же лишь немногие теоретические модели объясняют, как волатильность вообще возникает.

Ролл (1984) показывает, что волатильность зависит от микроструктуры рынка . ^[3] Глостен и Милгром (1985) показывают, что по крайней мере один источник волатильности можно объяснить процессом предоставления ликвидности. Когда маркет-мейкеры предполагают возможность неблагоприятного выбора , они корректируют свои торговые диапазоны, что в свою очередь увеличивает диапазон колебаний цен. ^[4]

В сентябре 2019 года JPMorgan Chase определил эффект твитов президента США Дональда Трампа и назвал его индексом Вольфефе, объединяющим волатильность и мем ковфефе .

Волатильность для инвесторов

Волатильность важна для инвесторов по крайней мере по восьми причинам, ^{[ необходима ссылка ]} некоторые из которых являются альтернативными утверждениями об одной и той же характеристике или напрямую вытекают друг из друга:

1. Чем сильнее колебания цен на инвестиции, тем сложнее эмоционально не беспокоиться;
2. Волатильность цены торгового инструмента может помочь определить размер позиции в портфеле;
3. Когда денежные потоки от продажи ценных бумаг необходимы в определенную будущую дату для покрытия известного фиксированного обязательства, более высокая волатильность означает большую вероятность дефицита;
4. Более высокая волатильность доходности при пенсионных накоплениях приводит к более широкому распределению возможных конечных стоимостей портфеля;
5. Более высокая волатильность доходов после выхода на пенсию может привести к тому, что изъятия окажут более сильное постоянное влияние на стоимость портфеля;
6. Волатильность цен дает возможность любому, у кого есть инсайдерская информация, покупать активы дешево и продавать их по завышенной цене;
7. Волатильность влияет на ценообразование опционов , являясь параметром модели Блэка-Шоулза .

Волатильность против направления

Волатильность не измеряет направление изменения цен, а только их дисперсию. Это происходит потому, что при расчете стандартного отклонения (или дисперсии ) все разницы возводятся в квадрат, так что отрицательные и положительные разницы объединяются в одну величину. Два инструмента с разной волатильностью могут иметь одинаковую ожидаемую доходность, но инструмент с более высокой волатильностью будет иметь большие колебания значений за определенный период времени.

Например, акции с более низкой волатильностью могут иметь ожидаемую (среднюю) доходность 7% с годовой волатильностью 5%. Игнорируя эффекты сложного процента, это будет указывать на доходность от приблизительно отрицательных 3% до положительных 17% большую часть времени (19 раз из 20, или 95% по правилу двух стандартных отклонений). Акции с более высокой волатильностью, с той же ожидаемой доходностью 7%, но с годовой волатильностью 20%, будут указывать на доходность от приблизительно отрицательных 33% до положительных 47% большую часть времени (19 раз из 20, или 95%). Эти оценки предполагают нормальное распределение ; в действительности движения цен на акции оказываются лептокуртотическими (с толстым хвостом).

Волатильность с течением времени

Хотя уравнение Блэка-Шоулза предполагает предсказуемую постоянную волатильность, это не наблюдается на реальных рынках. Среди более реалистичных моделей — локальная волатильность Эмануэля Дермана и Ираджа Кани ^[5] и Бруно Дюпира , процесс Пуассона , где волатильность переходит на новые уровни с предсказуемой частотой, и все более популярная модель стохастической волатильности Хестона . ^[6] [ссылка сломана]

Общеизвестно, что многие типы активов переживают периоды высокой и низкой волатильности. То есть, в некоторые периоды цены быстро растут и падают, а в другие периоды они почти не двигаются. ^[7] На валютном рынке изменения цен являются сезонно гетероскедастичными с периодами в один день и одну неделю. ^{[8] [9]}

Периоды, когда цены быстро падают ( обвал ), часто сменяются периодами, когда цены падают еще больше или растут на необычную величину. Также периоды, когда цены быстро растут (возможный пузырь ), часто могут сменяться периодами, когда цены растут еще больше или падают на необычную величину.

Чаще всего экстремальные движения не появляются «из ниоткуда»; они предвещаются более крупными движениями, чем обычно, или известной неопределенностью в определенных будущих событиях. Это называется авторегрессионной условной гетероскедастичностью . Имеют ли такие большие движения одинаковое направление или противоположное, сказать сложнее. И увеличение волатильности не всегда предвещает дальнейшее увеличение — волатильность может просто снова снизиться.

Меры волатильности зависят не только от периода, за который она измеряется, но и от выбранного временного разрешения, поскольку поток информации между краткосрочными и долгосрочными трейдерами асимметричен. ^{[ необходимо разъяснение ]} В результате волатильность, измеренная с высоким разрешением, содержит информацию, которая не охватывается волатильностью с низким разрешением, и наоборот. ^[10]

Взвешенная по паритету риска волатильность трех активов: золота, казначейских облигаций и Nasdaq, выступающих в качестве доверенного лица для Marketportfolio ^{[ необходимо разъяснение ],} по-видимому, достигла минимальной точки в 4% после того, как летом 2014 года она выросла в восьмой раз с 1974 года при таком же показателе. ^{[ необходимо разъяснение ] [ необходима цитата ]}

Альтернативные меры волатильности

Некоторые авторы отмечают, что реализованная волатильность и подразумеваемая волатильность являются ретроспективными и перспективными мерами и не отражают текущую волатильность. Для решения этой проблемы была предложена альтернатива — ансамблевые меры волатильности. Одна из мер определяется как стандартное отклонение ансамблевых доходностей вместо временного ряда доходностей. ^[11] Другая рассматривает регулярную последовательность направленных изменений как прокси для мгновенной волатильности. ^[12]

Волатильность и ее связь с торговлей опционами

Один из методов измерения волатильности, часто используемый компаниями, занимающимися количественной торговлей опционами, делит волатильность на два компонента. Чистая волатильность — величина волатильности, вызванная стандартными событиями, такими как ежедневные транзакции и общий шум, и грязная волатильность, величина, вызванная определенными событиями, такими как объявления о доходах или политике. ^[13] Например, у такой компании, как Microsoft, чистая волатильность была бы вызвана людьми, покупающими и продающими на ежедневной основе, но грязная (или событийная волатильность) событиями, такими как квартальные доходы или возможное объявление о нарушении антимонопольного законодательства.

Разбиение волатильности на два компонента полезно для точной оценки стоимости опциона, особенно при определении событий, которые могут способствовать колебанию. Работа фундаментальных аналитиков в маркет-мейкерах и бутик-фирмах опционной торговли обычно заключается в попытках присвоить этим числам числовые значения.

Параметризация подразумеваемой волатильности

Существует несколько известных параметризаций поверхности подразумеваемой волатильности: Шёнбухер, SVI и gSVI. ^[14]

Оценка волатильности сырой нефти

Используя упрощение вышеприведенной формулы, можно оценить годовую волатильность, основываясь исключительно на приблизительных наблюдениях. Предположим, вы заметили, что индекс рыночных цен, имеющий текущее значение около 10 000, в среднем двигался примерно на 100 пунктов в день в течение многих дней. Это будет составлять 1% ежедневного движения вверх или вниз.

Чтобы перевести это в годовой формат, можно использовать «правило 16», то есть умножить на 16, чтобы получить 16% годовой волатильности. Обоснованием этого является то, что 16 — это квадратный корень из 256, что приблизительно равно количеству торговых дней в году (252). Здесь также используется тот факт, что стандартное отклонение суммы n независимых переменных (с равными стандартными отклонениями) равно √n, умноженному на стандартное отклонение отдельных переменных.

Однако важно отметить, что это не учитывает (или в некоторых случаях может придавать чрезмерное значение) случайным крупным изменениям рыночной цены, которые происходят реже одного раза в год.

Средняя величина наблюдений — это всего лишь приближение стандартного отклонения рыночного индекса. Предполагая, что ежедневные изменения рыночного индекса распределены нормально со средним значением нулевым и стандартным отклонением  σ , ожидаемое значение величины наблюдений составляет √(2/ π ) σ = 0,798 σ . Чистый эффект заключается в том, что этот грубый подход недооценивает истинную волатильность примерно на 20%.

Оценка среднегодового темпа роста (CAGR)

Рассмотрим ряд Тейлора :

${\displaystyle \log(1+y)=y-{\tfrac {1}{2}}y^{2}+{\tfrac {1}{3}}y^{3}-{\tfrac {1}{4}}y^{4}+\cdots }$

Взяв только первые два члена, имеем:

${\displaystyle \mathrm {CAGR} \approx \mathrm {AR} -{\tfrac {1}{2}}\sigma ^{2}}$

Таким образом, волатильность математически представляет собой торможение CAGR (формализованное как « налог на волатильность »). Реалистично, большинство финансовых активов имеют отрицательную асимметрию и лептокуртозис, поэтому эта формула имеет тенденцию быть чрезмерно оптимистичной. Некоторые люди используют формулу:

${\displaystyle \mathrm {CAGR} \approx \mathrm {AR} -{\tfrac {1}{2}}k\sigma ^{2}}$

для приблизительной оценки, где k — эмпирический фактор (обычно от пяти до десяти). ^{[ необходима ссылка ]}

Критика моделей прогнозирования волатильности

Эффективность VIX (слева) по сравнению с прошлой волатильностью (справа) в качестве 30-дневных предсказателей волатильности за период с января 1990 г. по сентябрь 2009 г. Волатильность измеряется как стандартное отклонение однодневной доходности S&P500 за месячный период. Синие линии обозначают линейные регрессии , что приводит к показанным коэффициентам корреляции r . Обратите внимание, что VIX имеет практически такую ​​же предсказательную силу, как и прошлая волатильность, поскольку показанные коэффициенты корреляции почти идентичны.

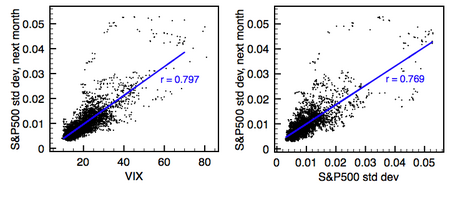
Несмотря на сложную структуру большинства моделей прогнозирования волатильности, критики утверждают, что их предсказательная сила аналогична предсказательной силе простых мер, таких как простая прошлая волатильность ^{[15] [16],} особенно вне выборки, где разные данные используются для оценки моделей и их тестирования. ^[17] Другие работы соглашаются, но утверждают, что критики не смогли правильно реализовать более сложные модели. ^[18] Некоторые практики и управляющие портфелями, похоже, полностью игнорируют или отвергают модели прогнозирования волатильности. Например, Нассим Талеб назвал одну из своих статей в журнале Journal of Portfolio Management «Мы не совсем знаем, о чем говорим, когда говорим о волатильности». ^[19] В похожей заметке Эмануэль Дерман выразил свое разочарование огромным запасом эмпирических моделей, не подкрепленных теорией. ^[20] Он утверждает, что, хотя «теории являются попытками раскрыть скрытые принципы, лежащие в основе окружающего нас мира, как это сделал Альберт Эйнштейн с его теорией относительности», мы должны помнить, что «модели являются метафорами – аналогиями, которые описывают одну вещь относительно другой».

Смотрите также

• Бета (финансы)  – ожидаемое изменение цены акции относительно всего рынка.
• Дисперсия  – статистическое свойство, количественно определяющее, насколько распределен набор данных.
• Финансовая экономика  – академическая дисциплина, изучающая обмен денег.
• IVX  – внутридневной индекс волатильности, подобный VIX, для американских ценных бумаг и биржевых инструментов
• Жюль Реньо  – французский экономистСтраницы, отображающие описания викиданных в качестве резерва
• Риск  – вероятность того, что произойдет что-то плохое
• VIX  – Индекс волатильности
• Улыбка волатильности  – подразумеваемые модели волатильности, возникающие при ценообразовании финансовых опционов.
• Налог на волатильность  – математический финансовый термин
• Риск волатильности
• Волатильность бета

Ссылки

1. "Распределение Леви". wilmottwiki.com .
2. "Расчет исторической волатильности: пошаговый пример" (PDF) . Архивировано из оригинала 30 марта 2012 . Получено 18 августа 2011 .{{cite web}}: CS1 maint: бот: исходный статус URL неизвестен ( ссылка )
3. Ролл, Р. (1984): «Простая неявная мера эффективного спреда между ценой покупки и продажи на эффективном рынке», Журнал финансов 39 (4), 1127–1139
4. Глостен, Л.Р. и П.Р. Милгром (1985): «Цены спроса, предложения и транзакции на специализированном рынке с неоднородно информированными трейдерами», Журнал финансовой экономики 14 (1), 71–100
5. Дерман, Э., Ирадж Кани (1994). ""Верхом на улыбке." RISK, 7(2) февраль 1994, стр. 139–145, стр. 32–39" (PDF) . Риск. Архивировано из оригинала (PDF) 10 июля 2011 г. . Получено 1 июня 2007 г. . {{cite journal}}: Цитировать журнал требует |journal=( помощь )CS1 maint: несколько имен: список авторов ( ссылка )
6. «Волатильность». wilmottwiki.com .
7. «Использование скачков волатильности с помощью кредитных спредов».
8. Мюллер, Ульрих А.; Дакоронья, Мишель М.; Ольсен, Ричард Б.; Пикте, Оливье В.; Шварц, Маттиас; Моргенегг, Клод (1 декабря 1990 г.). «Статистическое исследование валютных курсов, эмпирические доказательства закона масштабирования изменения цен и внутридневной анализ». Журнал банковского дела и финансов . 14 (6): 1189–1208. doi :10.1016/0378-4266(90)90009-Q. ISSN  0378-4266.
9. Петров, Владимир; Голуб, Антон; Олсен, Ричард (июнь 2019 г.). «Мгновенная сезонность волатильности высокочастотных рынков в направленном времени изменения внутреннего времени». Журнал риска и финансового менеджмента . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .
10. Мюллер, Ульрих А.; Дакоронья, Мишель; Дэйв, Рахаль Д.; Олсен, Ричард; Пикте, Оливье В.; фон Вайцзеккер, Якоб (1997). «Волатильности с различным временным разрешением — анализ динамики рыночных компонентов». Журнал эмпирических финансов . 4 (2–3): 213–239. doi :10.1016/S0927-5398(97)00007-8. ISSN  0927-5398.
11. Саркисян, Джек (2016). «Экспресс-измерение волатильности рынка с использованием концепции эргодичности». doi : 10.2139/ssrn.2812353. S2CID  168496910. SSRN  2812353. {{cite journal}}: Цитировать журнал требует |journal=( помощь )
12. Петров, Владимир; Голуб, Антон; Олсен, Ричард (июнь 2019 г.). «Мгновенная сезонность волатильности высокочастотных рынков в направленном времени изменения внутреннего времени». Журнал риска и финансового менеджмента . 12 (2): 54. doi : 10.3390/jrfm12020054 . hdl : 10419/239003 .
13. "Cleaning Implied Vols". Moontowermeta . Получено 26 июня 2024 г. .
14. Бабак Махдави Дамгани и Эндрю Кос (2013). «Деарбитраж со слабой улыбкой». Уилмотт. {{cite journal}}: Цитировать журнал требует |journal=( помощь ) http://www.readcube.com/articles/10.1002/wilm.10201?locale=en
15. Камби, Р.; Фиглевски, С.; Хасбрук, Дж. (1993). «Прогнозирование волатильности и корреляций с помощью моделей EGARCH». Журнал Derivatives . 1 (2): 51–63. doi :10.3905/jod.1993.407877. S2CID  154028452.
16. Джорион, П. (1995). «Прогнозирование волатильности на валютном рынке». Журнал финансов . 50 (2): 507–528. doi :10.1111/j.1540-6261.1995.tb04793.x. JSTOR  2329417.
17. Брукс, Крис ; Персанд, Гита (2003). «Прогнозирование волатильности для управления рисками». Журнал прогнозирования . 22 (1): 1–22. CiteSeerX 10.1.1.595.9113 . doi :10.1002/for.841. ISSN  1099-131X. S2CID  154615850. 
18. Андерсен, Торбен Г.; Боллерслев, Тим (1998). «Ответ скептикам: да, стандартные модели волатильности дают точные прогнозы». International Economic Review . 39 (4): 885–905. CiteSeerX 10.1.1.28.454 . doi :10.2307/2527343. JSTOR  2527343. 
19. Голдштейн, Дэниел и Талеб, Нассим (28 марта 2007 г.) «Мы не совсем понимаем, о чем говорим, когда говорим о волатильности». Журнал управления портфелем 33 (4), 2007.
20. Дерман, Эмануэль (2011): Модели.Плохое.поведение: почему путаница иллюзий с реальностью может привести к катастрофе на Уолл-стрит и в жизни», ред. Free Press.

Внешние ссылки

• Графическое сравнение подразумеваемой и исторической волатильности ^{[ постоянная мертвая ссылка ]} , видео
• Диболд, Фрэнсис X.; Хикман, Эндрю; Иноуэ, Ацуши и Шуерманн, Тил (1996) «Преобразование однодневной волатильности в h-дневную волатильность: масштабирование по sqrt(h) хуже, чем вы думаете»
• Краткое введение в альтернативные математические концепции волатильности
• Оценка волатильности на основе прогнозируемой плотности доходности. Пример основан на ежедневном распределении доходности Google с использованием стандартной функции плотности.
• Научная работа, включающая выдержку из отчета под названием «Определение высокой и дешевой волатильности. Выдержка из Enhanced Call Overwriting», отчета Райана Реникера и Деваприи Маллик из Lehman Brothers (2005).

Дальнейшее чтение

• Bartram, Söhnke M.; Brown, Gregory W.; Stulz, Rene M. (август 2012 г.). «Почему акции США более волатильны?» (PDF) . Journal of Finance . 67 (4): 1329–1370. doi :10.1111/j.1540-6261.2012.01749.x. S2CID  18587238. SSRN  2257549.
• Натенберг, Шелдон (2015). Волатильность и ценообразование опционов: передовые торговые стратегии и методы (второе издание). Нью-Йорк. ISBN 978-0071818773.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )