Естественная трансформация

Центральный объект исследования в теории категорий

В теории категорий , разделе математики , естественное преобразование обеспечивает способ преобразования одного функтора в другой с учетом внутренней структуры (т. е. композиции морфизмов ) вовлеченных категорий . Следовательно, естественное преобразование можно считать «морфизмом функторов». Неформально, понятие естественного преобразования утверждает, что определенное отображение между функторами может быть выполнено согласованно по всей категории.

Действительно, эта интуиция может быть формализована для определения так называемых категорий функторов . Естественные преобразования являются, после категорий и функторов, одним из самых фундаментальных понятий теории категорий и, следовательно, появляются в большинстве ее приложений.

Определение

Если и являются функторами между категориями и (оба из в ), то естественное преобразование из в представляет собой семейство морфизмов, удовлетворяющее двум требованиям. ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle \eta }$ ${\displaystyle F}$ ${\displaystyle G}$

1. Естественное преобразование должно связать с каждым объектом в морфизм между объектами из . Морфизм называется компонентом в . ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle \eta _{X}:F(X)\to G(X)}$ ${\displaystyle D}$ ${\displaystyle \eta _{X}}$ ${\displaystyle \eta }$ ${\displaystyle X}$
2. Компоненты должны быть такими, чтобы для каждого морфизма в мы имели: ${\displaystyle f:X\to Y}$ ${\displaystyle C}$

${\displaystyle \eta _{Y}\circ F(f)=G(f)\circ \eta _{X}}$

Последнее уравнение удобно выразить коммутативной диаграммой

Это коммутативная диаграмма, которая является частью определения естественного преобразования между двумя функторами.

Если и контравариантны , вертикальные стрелки на правой диаграмме меняются местами. Если — естественное преобразование из в , мы также пишем или . Это также выражается тем , что семейство морфизмов является естественным в . ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle \eta }$ ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle \eta :F\to G}$ ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \eta _{X}:F(X)\to G(X)}$ ${\displaystyle X}$

Если для каждого объекта в морфизм является изоморфизмом в , то говорят, что это ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle \eta _{X}}$ ${\displaystyle D}$ ${\displaystyle \eta }$естественный изоморфизм (или иногдаестественная эквивалентностьилиизоморфизм функторов). Два функтораиназываютсяестественно изоморфнымиили простоизоморфными,если существует естественный изоморфизм изв. ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle F}$ ${\displaystyle G}$

Инфраестественное преобразование из в — это просто семейство морфизмов для всех в . Таким образом, естественное преобразование — это инфраестественное преобразование, для которого для каждого морфизма . Натурализатор , nat , — это самая большая подкатегория из , содержащая все объекты из , на которой ограничивается естественным преобразованием. ${\displaystyle \eta }$ ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle \eta _{X}:F(X)\to G(X)}$ ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle \eta _{Y}\circ F(f)=G(f)\circ \eta _{X}}$ ${\displaystyle f:X\to Y}$ ${\displaystyle \eta }$ ${\displaystyle (\eta )}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle \eta }$

Примеры

Противоположная группа

Такие заявления, как

«Каждая группа естественно изоморфна своей противоположной группе »

изобилуют в современной математике. Сейчас мы дадим точное значение этого утверждения, а также его доказательство. Рассмотрим категорию всех групп с групповыми гомоморфизмами как морфизмами. Если — группа, мы определяем ее противоположную группу следующим образом: — то же самое множество, что и , а операция определяется как . Таким образом, все умножения в «переворачиваются». Формирование противоположной группы становится (ковариантным) функтором из в , если мы определим для любого группового гомоморфизма . Обратите внимание, что — действительно групповой гомоморфизм из в : ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle (G,*)}$ ${\displaystyle (G^{\text{op}},{*}^{\text{op}})}$ ${\displaystyle G^{\text{op}}}$ ${\displaystyle G}$ ${\displaystyle *^{\text{op}}}$ ${\displaystyle a*^{\text{op}}b=b*a}$ ${\displaystyle G^{\text{op}}}$ ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle f^{\text{op}}=f}$ ${\displaystyle f:G\to H}$ ${\displaystyle f^{\text{op}}}$ ${\displaystyle G^{\text{op}}}$ ${\displaystyle H^{\text{op}}}$

${\displaystyle f^{\text{op}}(a*^{\text{op}}b)=f(b*a)=f(b)*f(a)=f^{\text{op}}(a)*^{\text{op}}f^{\text{op}}(b).}$

Содержание вышеуказанного заявления следующее:

"Тождественный функтор естественно изоморфен противоположному функтору " ${\displaystyle {\text{Id}}_{\textbf {Grp}}:{\textbf {Grp}}\to {\textbf {Grp}}}$ ${\displaystyle {\text{op}}:{\textbf {Grp}}\to {\textbf {Grp}}}$

Чтобы доказать это, нам нужно предоставить изоморфизмы для каждой группы , такие, что приведенная выше диаграмма коммутирует. Положим . Формулы и показывают, что является гомоморфизмом групп с обратным . Чтобы доказать естественность, мы начнем с гомоморфизма групп и покажем , т.е. для всех в . Это верно, поскольку и каждый гомоморфизм групп обладает свойством . ${\displaystyle \eta _{G}:G\to G^{\text{op}}}$ ${\displaystyle G}$ ${\displaystyle \eta _{G}(a)=a^{-1}}$ ${\displaystyle (a*b)^{-1}=b^{-1}*a^{-1}=a^{-1}*^{\text{op}}b^{-1}}$ ${\displaystyle (a^{-1})^{-1}=a}$ ${\displaystyle \eta _{G}}$ ${\displaystyle \eta _{G^{\text{op}}}}$ ${\displaystyle f:G\to H}$ ${\displaystyle \eta _{H}\circ f=f^{\text{op}}\circ \eta _{G}}$ ${\displaystyle (f(a))^{-1}=f^{\text{op}}(a^{-1})}$ ${\displaystyle a}$ ${\displaystyle G}$ ${\displaystyle f^{\text{op}}=f}$ ${\displaystyle (f(a))^{-1}=f(a^{-1})}$

Модули

Пусть будет гомоморфизмом правых модулей -модулей. Для каждого левого модуля существует естественное отображение , образующее естественное преобразование . Для каждого правого модуля существует естественное отображение , определяемое , образующее естественное преобразование . ${\displaystyle \varphi :M\longrightarrow M^{\prime }}$ ${\displaystyle R}$ ${\displaystyle N}$ ${\displaystyle \varphi \otimes N:M\otimes _{R}N\longrightarrow M^{\prime }\otimes _{R}N}$ ${\displaystyle \eta :M\otimes _{R}-\implies M'\otimes _{R}-}$ ${\displaystyle N}$ ${\displaystyle \eta _{N}:{\text{Hom}}_{R}(M',N)\longrightarrow {\text{Hom}}_{R}(M,N)}$ ${\displaystyle \eta _{N}(f)=f\varphi }$ ${\displaystyle \eta :{\text{Hom}}_{R}(M',-)\implies {\text{Hom}}_{R}(M,-)}$

Абелианизация

Для данной группы мы можем определить ее абелианизацию . Пусть обозначает проекционное отображение на смежные классы . Этот гомоморфизм является «естественным в », т.е. он определяет естественное преобразование, которое мы сейчас проверим. Пусть будет группой. Для любого гомоморфизма , мы имеем , что содержится в ядре , поскольку любой гомоморфизм в абелеву группу убивает коммутантную подгруппу. Затем разлагаем как для единственного гомоморфизма . Это создает функтор и естественное преобразование, но не естественный изоморфизм, из тождественного функтора в . ${\displaystyle G}$ ${\displaystyle G^{\text{ab}}=G/}$ ${\displaystyle [G,G]}$ ${\displaystyle \pi _{G}:G\to G^{\text{ab}}}$ ${\displaystyle [G,G]}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle f:G\to H}$ ${\displaystyle [G,G]}$ ${\displaystyle \pi _{H}\circ f}$ ${\displaystyle \pi _{H}\circ f}$ ${\displaystyle G^{\text{ab}}}$ ${\displaystyle f^{\text{ab}}\circ \pi _{G}=\pi _{H}\circ f}$ ${\displaystyle f^{\text{ab}}:G^{\text{ab}}\to H^{\text{ab}}}$ ${\displaystyle {\text{ab}}:{\textbf {Grp}}\to {\textbf {Grp}}}$ ${\displaystyle \pi }$ ${\displaystyle {\text{ab}}}$

Гомоморфизм Гуревича

Функторы и естественные преобразования изобилуют в алгебраической топологии , и гомоморфизмы Гуревича служат примерами. Для любого топологического пространства с точкой и положительного целого числа существует групповой гомоморфизм ${\displaystyle (X,x)}$ ${\displaystyle n}$

${\displaystyle h_{n}\colon \pi _{n}(X,x)\to H_{n}(X)}$

из -й гомотопической группы в -ю гомологическую группу . Оба функтора и являются функторами из категории Top ^* точечных топологических пространств в категорию Grp групп, и является естественным преобразованием из в . ${\displaystyle n}$ ${\displaystyle (X,x)}$ ${\displaystyle n}$ ${\displaystyle X}$ ${\displaystyle \pi _{n}}$ ${\displaystyle H_{n}}$ ${\displaystyle h_{n}}$ ${\displaystyle \pi _{n}}$ ${\displaystyle H_{n}}$

Определитель

При наличии коммутативных колец и с кольцевым гомоморфизмом соответствующие группы обратимых матриц и наследуют гомоморфизм, который мы обозначаем как , полученный применением к каждому элементу матрицы. Аналогично, ограничивается до группового гомоморфизма , где обозначает группу единиц . Фактически, и являются функторами из категории коммутативных колец в . Определитель на группе , обозначаемый как , является групповым гомоморфизмом ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle f:R\to S}$ ${\displaystyle n\times n}$ ${\displaystyle {\text{GL}}_{n}(R)}$ ${\displaystyle {\text{GL}}_{n}(S)}$ ${\displaystyle {\text{GL}}_{n}(f)}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f^{*}:R^{*}\to S^{*}}$ ${\displaystyle R^{*}}$ ${\displaystyle R}$ ${\displaystyle {\text{GL}}_{n}}$ ${\displaystyle *}$ ${\displaystyle {\textbf {CRing}}}$ ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle {\text{GL}}_{n}(R)}$ ${\displaystyle {\text{det}}_{R}}$

${\displaystyle {\mbox{det}}_{R}\colon {\mbox{GL}}_{n}(R)\to R^{*}}$

что естественно в : поскольку определитель определяется той же формулой для каждого кольца, выполняется. Это делает определитель естественным преобразованием из в . ${\displaystyle R}$ ${\displaystyle f^{*}\circ {\text{det}}_{R}={\text{det}}_{S}\circ {\text{GL}}_{n}(f)}$ ${\displaystyle {\text{GL}}_{n}}$ ${\displaystyle *}$

Двойной дуал векторного пространства

Например, если является полем , то для любого векторного пространства над мы имеем «естественное» инъективное линейное отображение из векторного пространства в его двойной дуальный . Эти отображения являются «естественными» в следующем смысле: двойная дуальная операция является функтором, а отображения являются компонентами естественного преобразования из тождественного функтора в двойной дуальный функтор. ${\displaystyle K}$ ${\displaystyle V}$ ${\displaystyle K}$ ${\displaystyle V\to V^{**}}$

Конечное исчисление

Для каждой абелевой группы набор функций от целых чисел до базового набора образует абелеву группу при поточечном сложении. (Вот стандартный забывающий функтор .) При наличии морфизма отображение, заданное левым составлением с элементами первого, само является гомоморфизмом абелевых групп; таким образом, мы получаем функтор . Оператор конечной разности, переводящий каждую функцию в , является отображением из в себя, и набор таких отображений дает естественное преобразование . ${\displaystyle G}$ ${\displaystyle {\text{Hom}}_{\textbf {Set}}(\mathbb {Z} ,U(G))}$ ${\displaystyle G}$ ${\displaystyle V_{\mathbb {Z} }(G)}$ ${\displaystyle U}$ ${\displaystyle U:{\textbf {Ab}}\to {\textbf {Set}}}$ ${\displaystyle {\textbf {Ab}}}$ ${\displaystyle \varphi :G\to G'}$ ${\displaystyle V_{\mathbb {Z} }(\varphi ):V_{\mathbb {Z} }(G)\to V_{\mathbb {Z} }(G')}$ ${\displaystyle \varphi }$ ${\displaystyle V_{\mathbb {Z} }:{\textbf {Ab}}\to {\textbf {Ab}}}$ ${\displaystyle \Delta _{G}}$ ${\displaystyle f:\mathbb {Z} \to U(G)}$ ${\displaystyle \Delta (f):n\mapsto f(n+1)-f(n)}$ ${\displaystyle V_{\mathbb {Z} }(G)}$ ${\displaystyle \Delta }$ ${\displaystyle \Delta :V_{\mathbb {Z} }\to V_{\mathbb {Z} }}$

Тензорно-гомозное присоединение

Рассмотрим категорию ${\displaystyle {\textbf {Ab}}}$ абелевых групп и гомоморфизмы групп. Для всех абелевых групп и имеем изоморфизм групп ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Z}$

${\displaystyle {\text{Hom}}(X\otimes Y,Z)\to {\text{Hom}}(X,{\text{Hom}}(Y,Z))}$.

Эти изоморфизмы являются «естественными» в том смысле, что они определяют естественное преобразование между двумя вовлеченными функторами . (Здесь «op» — это противоположная категория , не путать с тривиальным противоположным групповым функтором на  !) ${\displaystyle {\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}\to {\textbf {Ab}}}$ ${\displaystyle {\textbf {Ab}}}$ ${\displaystyle {\textbf {Ab}}}$

Это формально тензорно-гомовое сопряжение и является архетипическим примером пары сопряженных функторов . Естественные преобразования часто возникают в сочетании с сопряженными функторами, и действительно, сопряженные функторы определяются определенным естественным изоморфизмом. Кроме того, каждая пара сопряженных функторов оснащена двумя естественными преобразованиями (обычно не изоморфизмами), называемыми единицей и коединицей .

Неестественный изоморфизм

Понятие естественного преобразования является категоричным и утверждает (неформально), что конкретное отображение между функторами может быть выполнено последовательно по всей категории. Неформально конкретное отображение (особенно изоморфизм) между отдельными объектами (не целыми категориями) называется «естественным изоморфизмом», что подразумевает, что оно фактически определено для всей категории и определяет естественное преобразование функторов; формализация этой интуиции была мотивирующим фактором в развитии теории категорий.

Наоборот, конкретное отображение между конкретными объектами может быть названо неестественным изоморфизмом (или «изоморфизмом, который не является естественным»), если отображение не может быть расширено до естественного преобразования на всю категорию. Для данного объекта функтор (для простоты принимая первый функтор за тождество) и изоморфизм доказательство неестественности проще всего показать, указав автоморфизм , который не коммутирует с этим изоморфизмом (так что ). Более того, если кто-то хочет доказать, что и не являются естественно изоморфными, без ссылки на конкретный изоморфизм, это требует показать, что для любого изоморфизма есть некоторые , с которыми он не коммутирует; в некоторых случаях один автоморфизм работает для всех кандидатов на изоморфизмы, в то время как в других случаях нужно показать, как построить другой для каждого изоморфизма. Карты категории играют решающую роль — любое инфраестественное преобразование является естественным, если единственными картами являются тождественные карты, например. ${\displaystyle X,}$ ${\displaystyle G}$ ${\displaystyle \eta \colon X\to G(X),}$ ${\displaystyle A\colon X\to X}$ ${\displaystyle \eta \circ A\neq G(A)\circ \eta }$ ${\displaystyle X}$ ${\displaystyle G(X)}$ ${\displaystyle \eta }$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \eta }$ ${\displaystyle A_{\eta }}$

Это похоже (но более категорично) на концепции в теории групп или теории модулей, где заданное разложение объекта в прямую сумму «не является естественным» или, скорее, «не единственным», поскольку существуют автоморфизмы, которые не сохраняют разложение в прямую сумму – см., например, Структурную теорему для конечно порожденных модулей над областью главных идеалов § Единственность .

Некоторые авторы различают обозначения, используя для естественного изоморфизма и для неестественного изоморфизма, оставляя за собой равенство (обычно равенство отображений). ${\displaystyle \cong }$ ${\displaystyle \approx }$ ${\displaystyle =}$

Пример: фундаментальная группа тора

В качестве примера различия между функториальным утверждением и индивидуальными объектами рассмотрим гомотопические группы пространства-произведения, в частности фундаментальную группу тора.

Гомотопические группы пространства-произведения естественным образом являются произведениями гомотопических групп компонентов, причем изоморфизм задается проекцией на два множителя, по сути, потому, что отображения в пространство-произведение являются в точности произведениями отображений в компоненты – это функториальное утверждение. ${\displaystyle \pi _{n}((X,x_{0})\times (Y,y_{0}))\cong \pi _{n}((X,x_{0}))\times \pi _{n}((Y,y_{0})),}$

Однако тор (который абстрактно является произведением двух окружностей) имеет фундаментальную группу, изоморфную , но расщепление не является естественным. Обратите внимание на использование , , и : ^[a] ${\displaystyle Z^{2}}$ ${\displaystyle \pi _{1}(T,t_{0})\approx \mathbf {Z} \times \mathbf {Z} }$ ${\displaystyle \approx }$ ${\displaystyle \cong }$ ${\displaystyle =}$

${\displaystyle \pi _{1}(T,t_{0})\approx \pi _{1}(S^{1},x_{0})\times \pi _{1}(S^{1},y_{0})\cong \mathbf {Z} \times \mathbf {Z} =\mathbf {Z} ^{2}.}$

Этот абстрактный изоморфизм с произведением не является естественным, так как некоторые изоморфизмы не сохраняют произведение: самогомеоморфизм (рассматриваемый как фактор-пространство ), заданный (геометрически скручиванием Дена вокруг одной из порождающих кривых), действует как эта матрица на (она находится в общей линейной группе обратимых целочисленных матриц), что не сохраняет разложение как произведение, поскольку оно не является диагональным. Однако, если дан тор как произведение — эквивалентно, дано разложение пространства — то расщепление группы следует из общего утверждения ранее. В категориальных терминах соответствующая категория (сохраняющая структуру пространства произведения) — это «карты пространств произведений, а именно пара карт между соответствующими компонентами». ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle R^{2}/\mathbb {Z} ^{2}}$ ${\displaystyle \left({\begin{smallmatrix}1&1\\0&1\end{smallmatrix}}\right)}$ ${\displaystyle \mathbb {Z} ^{2}}$ ${\displaystyle {\text{GL}}(\mathbb {Z} ,2)}$ ${\displaystyle (T,t_{0})=(S^{1},x_{0})\times (S^{1},y_{0})}$

Естественность — это категориальное понятие, требующее большой точности в отношении того, какие именно данные даны: тор как пространство, которое оказывается произведением (в категории пространств и непрерывных отображений), отличается от тора, представленного как произведение (в категории произведений двух пространств и непрерывных отображений между соответствующими компонентами).

Пример: двойственное к конечномерному векторному пространству

Каждое конечномерное векторное пространство изоморфно своему двойственному пространству, но между этими двумя пространствами может быть много различных изоморфизмов. В общем случае нет естественного изоморфизма между конечномерным векторным пространством и его двойственным пространством. ^[1] Однако связанные категории (с дополнительной структурой и ограничениями на отображения) имеют естественный изоморфизм, как описано ниже.

Двойственное пространство конечномерного векторного пространства снова является конечномерным векторным пространством той же размерности, и они, таким образом, изоморфны, поскольку размерность является единственным инвариантом конечномерных векторных пространств над заданным полем. Однако, в отсутствие дополнительных ограничений (таких как требование, чтобы отображения сохраняли выбранный базис), отображение из пространства в его двойственное не является единственным, и, таким образом, такой изоморфизм требует выбора и является «не естественным». В категории конечномерных векторных пространств и линейных отображений можно определить инфраестественный изоморфизм из векторных пространств в их двойственное, выбрав изоморфизм для каждого пространства (скажем, выбрав базис для каждого векторного пространства и взяв соответствующий изоморфизм), но это не определит естественное преобразование. Интуитивно это потому, что это требует выбора, строго потому, что любой такой выбор изоморфизмов не будет коммутировать, скажем, с нулевым отображением; см. (Mac Lane & Birkhoff 1999, §VI.4) для подробного обсуждения.

Начиная с конечномерных векторных пространств (как объектов) и тождественных и двойственных функторов, можно определить естественный изоморфизм, но для этого требуется сначала добавить дополнительную структуру, а затем ограничить отображения со «всех линейных отображений» до «линейных отображений, которые уважают эту структуру». Явно, для каждого векторного пространства, потребовать, чтобы оно поставлялось с данными изоморфизма к своему двойственному, . Другими словами, взять в качестве объектов векторные пространства с невырожденной билинейной формой . Это определяет инфраестественный изоморфизм (изоморфизм для каждого объекта). Затем ограничить отображения только теми отображениями , которые коммутируют с изоморфизмами: или, другими словами, сохранить билинейную форму: . (Эти отображения определяют натурализатор изоморфизмов.) Результирующая категория с объектами конечномерными векторными пространствами с невырожденной билинейной формой и отображениями линейных преобразований, которые уважают билинейную форму, по построению имеет естественный изоморфизм от тождества к двойственному (каждое пространство имеет изоморфизм к своему двойственному, и отображения в категории должны коммутировать). Рассматриваемая в этом свете эта конструкция (добавление преобразований для каждого объекта, ограничение отображений для коммутации с ними) является полностью общей и не зависит от каких-либо конкретных свойств векторных пространств. ${\displaystyle \eta _{V}\colon V\to V^{*}}$ ${\displaystyle b_{V}\colon V\times V\to K}$ ${\displaystyle T\colon V\to U}$ ${\displaystyle T^{*}(\eta _{U}(T(v)))=\eta _{V}(v)}$ ${\displaystyle b_{U}(T(v),T(w))=b_{V}(v,w)}$

В этой категории (конечномерные векторные пространства с невырожденной билинейной формой, отображения линейных преобразований, которые уважают билинейную форму), двойственное отображение между векторными пространствами может быть идентифицировано как транспонирование . Часто по причинам геометрического интереса это специфицируется в подкатегорию, требуя, чтобы невырожденные билинейные формы имели дополнительные свойства, такие как симметричность ( ортогональные матрицы ), симметричность и положительное определение ( пространство внутреннего произведения ), симметричная полуторалинейная ( эрмитовы пространства ), кососимметричная и полностью изотропная ( симплектическое векторное пространство ) и т. д. — во всех этих категориях векторное пространство естественным образом отождествляется со своим двойственным с помощью невырожденной билинейной формы.

Операции с естественными преобразованиями

Горизонтальная и вертикальная композиция природных преобразований

Вертикальная композиция

Если и являются естественными преобразованиями между функторами , то мы можем скомпоновать их, чтобы получить естественное преобразование . Это делается покомпонентно: ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \epsilon :G\Rightarrow H}$ ${\displaystyle F,G,H:C\to D}$ ${\displaystyle \epsilon \circ \eta :F\Rightarrow H}$

${\displaystyle (\epsilon \circ \eta )_{X}=\epsilon _{X}\circ \eta _{X}}$.

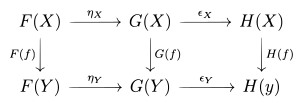
Эта вертикальная композиция естественных преобразований ассоциативна и имеет тождество, и позволяет рассматривать совокупность всех функторов как категорию (см. ниже в разделе Категории функторов). Тождественное естественное преобразование на функторе имеет компоненты . ^[2] ${\displaystyle C\to D}$ ${\displaystyle \mathrm {id} _{F}}$ ${\displaystyle F}$ ${\displaystyle (\mathrm {id} _{F})_{X}=\mathrm {id} _{F(X)}}$

Для , . ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \mathrm {id} _{G}\circ \eta =\eta =\eta \circ \mathrm {id} _{F}}$

Горизонтальная композиция

Если — естественное преобразование между функторами и — естественное преобразование между функторами , то композиция функторов допускает композицию естественных преобразований с компонентами ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle F,G:C\to D}$ ${\displaystyle \epsilon :J\Rightarrow K}$ ${\displaystyle J,K:D\to E}$ ${\displaystyle \epsilon *\eta :J\circ F\Rightarrow K\circ G}$

${\displaystyle (\epsilon *\eta )_{X}=\epsilon _{G(X)}\circ J(\eta _{X})=K(\eta _{X})\circ \epsilon _{F(X)}}$.

Используя усы (см. ниже), мы можем записать

${\displaystyle (\epsilon *\eta )_{X}=(\epsilon G)_{X}\circ (J\eta )_{X}=(K\eta )_{X}\circ (\epsilon F)_{X}}$,

следовательно

${\displaystyle \epsilon *\eta =\epsilon G\circ J\eta =K\eta \circ \epsilon F}$.

Эта горизонтальная композиция естественных преобразований также ассоциативна с тождеством. Это тождество является естественным преобразованием тождества на функторе тождества , т.е. естественным преобразованием, которое сопоставляет каждому объекту его морфизм тождества : для объекта в категории , . ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle (\mathrm {id} _{\mathrm {id} _{C}})_{X}=\mathrm {id} _{\mathrm {id} _{C}(X)}=\mathrm {id} _{X}}$

Для с , . ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle F,G:C\to D}$ ${\displaystyle \mathrm {id} _{\mathrm {id} _{D}}*\eta =\eta =\eta *\mathrm {id} _{\mathrm {id} _{C}}}$

Так как тождественные функторы и являются функторами, тождество для горизонтальной композиции является также тождеством для вертикальной композиции, но не наоборот. ^[3] ${\displaystyle \mathrm {id} _{C}}$ ${\displaystyle \mathrm {id} _{D}}$

Усы

Усы — это внешняя бинарная операция между функтором и естественным преобразованием. ^{[4] [5]}

Если — естественное преобразование между функторами , а — другой функтор, то мы можем сформировать естественное преобразование , определив ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle F,G:C\to D}$ ${\displaystyle H:D\to E}$ ${\displaystyle H\eta :H\circ F\Rightarrow H\circ G}$

${\displaystyle (H\eta )_{X}=H(\eta _{X})}$.

Если же — функтор, то естественное преобразование определяется как ${\displaystyle K:B\to C}$ ${\displaystyle \eta K:F\circ K\Rightarrow G\circ K}$

${\displaystyle (\eta K)_{X}=\eta _{K(X)}}$.

Это также горизонтальная композиция, где одним из естественных преобразований является естественное преобразование тождества:

${\displaystyle H\eta =\mathrm {id} _{H}*\eta }$и . ${\displaystyle \eta K=\eta *\mathrm {id} _{K}}$

Обратите внимание, что (соответственно ) обычно не является левым (соответственно правым) тождеством горизонтальной композиции ( и в общем случае), за исключением случая, когда (соответственно ) является тождественным функтором категории (соответственно ). ${\displaystyle \mathrm {id} _{H}}$ ${\displaystyle \mathrm {id} _{K}}$ ${\displaystyle *}$ ${\displaystyle H\eta \neq \eta }$ ${\displaystyle \eta K\neq \eta }$ ${\displaystyle H}$ ${\displaystyle K}$ ${\displaystyle D}$ ${\displaystyle C}$

Закон о взаимозачете

Эти две операции связаны тождеством, которое меняет местами вертикальную композицию и горизонтальную композицию: если у нас есть четыре естественных преобразования , как показано на рисунке справа, то справедливо следующее тождество: ${\displaystyle \alpha ,\alpha ',\beta ,\beta '}$

${\displaystyle (\beta '\circ \alpha ')*(\beta \circ \alpha )=(\beta '*\beta )\circ (\alpha '*\alpha )}$.

Вертикальные и горизонтальные композиции также связаны посредством тождественных естественных преобразований:

для и , . ^[6] ${\displaystyle F:C\to D}$ ${\displaystyle G:D\to E}$ ${\displaystyle \mathrm {id} _{G}*\mathrm {id} _{F}=\mathrm {id} _{G\circ F}}$

Поскольку усы представляют собой горизонтальную композицию с тождеством, закон взаимозаменяемости немедленно дает компактные формулы горизонтальной композиции и без необходимости анализа компонентов и коммутативной диаграммы: ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \epsilon :J\Rightarrow K}$

${\displaystyle {\begin{aligned}\epsilon *\eta &=(\epsilon \circ \mathrm {id} _{J})*(\mathrm {id} _{G}\circ \eta )=(\epsilon *\mathrm {id} _{G})\circ (\mathrm {id} _{J}*\eta )=\epsilon G\circ J\eta \\&=(\mathrm {id} _{K}\circ \epsilon )*(\eta \circ \mathrm {id} _{F})=(\mathrm {id} _{K}*\eta )\circ (\epsilon *\mathrm {id} _{F})=K\eta \circ \epsilon F\end{aligned}}}$.

Категории функторов

Если — любая категория и — малая категория , мы можем образовать категорию функторов, имеющую в качестве объектов все функторы из в и в качестве морфизмов естественные преобразования между этими функторами. Это образует категорию, поскольку для любого функтора существует тождественное естественное преобразование (которое назначает каждому объекту тождественный морфизм на ), а композиция двух естественных преобразований («вертикальная композиция» выше) снова является естественным преобразованием. ${\displaystyle C}$ ${\displaystyle I}$ ${\displaystyle C^{I}}$ ${\displaystyle I}$ ${\displaystyle C}$ ${\displaystyle F}$ ${\displaystyle 1_{F}:F\to F}$ ${\displaystyle X}$ ${\displaystyle F(X)}$

Изоморфизмы в являются именно естественными изоморфизмами. То есть, естественное преобразование является естественным изоморфизмом тогда и только тогда, когда существует естественное преобразование такое, что и . ${\displaystyle C^{I}}$ ${\displaystyle \eta :F\to G}$ ${\displaystyle \epsilon :G\to F}$ ${\displaystyle \eta \epsilon =1_{G}}$ ${\displaystyle \epsilon \eta =1_{F}}$

Категория функторов особенно полезна, если возникает из направленного графа . Например, если — категория направленного графа • → • , то имеет в качестве объектов морфизмы , а морфизм между и в — это пара морфизмов и в , такая, что «квадрат коммутирует», т.е. . ${\displaystyle C^{I}}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle C^{I}}$ ${\displaystyle C}$ ${\displaystyle \phi :U\to V}$ ${\displaystyle \psi :X\to Y}$ ${\displaystyle C^{I}}$ ${\displaystyle f:U\to X}$ ${\displaystyle g:V\to Y}$ ${\displaystyle C}$ ${\displaystyle \psi \circ f=g\circ \phi }$

В более общем смысле можно построить 2-категорию , ${\displaystyle {\textbf {Cat}}}$

• 0-клетки (объекты) — это малые категории,
• 1-клетки (стрелки) между двумя объектами и являются функторами из в , ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle C}$ ${\displaystyle D}$
• 2-клетки между двумя 1-клетками (функторы) и являются естественными преобразованиями из в . ${\displaystyle F:C\to D}$ ${\displaystyle G:C\to D}$ ${\displaystyle F}$ ${\displaystyle G}$

Горизонтальные и вертикальные композиции — это композиции между естественными преобразованиями, описанными ранее. Тогда категория функторов — это просто hom-категория в этой категории (оставим в стороне вопросы малости). ${\displaystyle C^{I}}$

Еще примеры

Каждый предел и копредел дает пример простого естественного преобразования, поскольку конус представляет собой естественное преобразование с диагональным функтором в качестве области. Действительно, если пределы и копределы определяются непосредственно в терминах их универсального свойства , они являются универсальными морфизмами в категории функторов.

лемма Йонеды

Если — объект локально малой категории , то присваивание определяет ковариантный функтор . Этот функтор называется представимым (в более общем смысле представимый функтор — это любой функтор, естественно изоморфный этому функтору для подходящего выбора ). Естественные преобразования из представимого функтора в произвольный функтор полностью известны и легко описываются; это содержание леммы Йонеды . ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle Y\mapsto {\text{Hom}}_{C}(X,Y)}$ ${\displaystyle F_{X}:C\to {\textbf {Set}}}$ ${\displaystyle X}$ ${\displaystyle F:C\to {\textbf {Set}}}$

Исторические заметки

Сондерс Маклейн , один из основателей теории категорий, как говорят, заметил: «Я не изобретал категории для изучения функторов; я изобрел их для изучения естественных преобразований». ^[7] Так же, как изучение групп не является полным без изучения гомоморфизмов , так и изучение категорий не является полным без изучения функторов . Причина комментария Маклейна в том, что изучение функторов само по себе не является полным без изучения естественных преобразований.

Контекстом замечания Маклейна была аксиоматическая теория гомологии . Можно было показать, что различные способы построения гомологии совпадают: например, в случае симплициального комплекса группы, определенные напрямую, были бы изоморфны группам сингулярной теории. Что не может быть легко выражено без языка естественных преобразований, так это то, как группы гомологии совместимы с морфизмами между объектами, и как две эквивалентные теории гомологии не только имеют одни и те же группы гомологии, но и одни и те же морфизмы между этими группами.

Смотрите также

• Математический портал

• Сверхъестественное преобразование
• Универсальная собственность
• Теория высшей категории

Примечания

1. Z ⁿ можно определить как n -кратное произведение Z , или как произведение Z ^{n  − 1} и Z , которые являются тонко различными множествами (хотя их можно естественным образом идентифицировать, что будет обозначено как ≅). Здесь мы зафиксировали определение, и в любом случае они совпадают при n  = 2.

Ссылки

1. (Мак Лейн и Биркгофф 1999, §VI.4)
2. «Естественное преобразование идентичности в nLab».
3. "Естественные трансформации". 7 апреля 2015 г.
4. «Определение:Усы — ProofWiki».
5. "Усы в nLab".
6. https://arxiv.org/pdf/1612.09375v1.pdf, стр. 38
7. (Мак Лейн 1998, §I.4)

• Mac Lane, Saunders (1998), Категории для работающих математиков , Graduate Texts in Mathematics 5 (2-е изд.), Springer-Verlag, стр. 16, ISBN 0-387-98403-8
• Мак Лейн, Сондерс ; Биркгофф, Гарретт (1999), Алгебра (3-е изд.), AMS Chelsea Publishing, ISBN 0-8218-1646-2.
• Аводей, Стив (2010). Теория категорий . Оксфорд, Нью-Йорк: Oxford University Press. стр. 156. ISBN 978-0199237180.
• Лейн, Сондерс (1992). Пучки в геометрии и логике: первое введение в теорию топосов . Нью-Йорк: Springer-Verlag. стр. 13. ISBN 0387977104.

Внешние ссылки

• nLab, вики-проект по математике, физике и философии с акцентом на n -категориальную точку зрения
• Дж. Адамек, Х. Херрлих, Г. Штреккер, Абстрактные и конкретные категории. Радость кошек
• Стэнфордская энциклопедия философии : «Теория категорий» — Жан-Пьер Марки. Обширная библиография.
• Баез, Джон, 1996, «Сказка об n-категориях». Неформальное введение в высшие категории.