Естественная трансформация

Центральный объект исследования теории категорий

В теории категорий , разделе математики , естественное преобразование обеспечивает способ преобразования одного функтора в другой, сохраняя при этом внутреннюю структуру (т. е. состав морфизмов ) задействованных категорий . Следовательно, естественное преобразование можно рассматривать как «морфизм функторов». Неформально, понятие естественного преобразования утверждает, что определенное отображение между функторами может быть выполнено последовательно для всей категории.

Действительно, эту интуицию можно формализовать, чтобы определить так называемые категории функторов . Естественные преобразования являются после категорий и функторов одним из наиболее фундаментальных понятий теории категорий и, следовательно, появляются в большинстве ее приложений.

Определение

Если и являются функторами между категориями и (обе от до ), то естественное преобразование от до представляет собой семейство морфизмов, удовлетворяющее двум требованиям. ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle \eta }$ ${\displaystyle F}$ ${\displaystyle G}$

1. Естественное преобразование должно связать с каждым объектом в морфизм между объектами из . Морфизм называется компонентой at .​ ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle \eta _{X}:F(X)\to G(X)}$ ${\displaystyle D}$ ${\displaystyle \eta _{X}}$ ${\displaystyle \eta }$ ${\displaystyle X}$
2. Компоненты должны быть такими, чтобы для каждого морфизма в мы имели: ${\displaystyle f:X\to Y}$ ${\displaystyle C}$

${\displaystyle \eta _{Y}\circ F(f)=G(f)\circ \eta _{X}}$

Последнее уравнение удобно выразить коммутативной диаграммой

Это коммутативная диаграмма, которая является частью определения естественного преобразования между двумя функторами.

Если оба и контравариантны , вертикальные стрелки на правой диаграмме меняются местами. Если – естественное преобразование из в , мы также пишем или . Это также выражается в том, что семейство морфизмов является естественным в . ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle \eta }$ ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle \eta :F\to G}$ ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \eta _{X}:F(X)\to G(X)}$ ${\displaystyle X}$

Если для каждого объекта в морфизм является изоморфизмом в , то говорят, что это ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle \eta _{X}}$ ${\displaystyle D}$ ${\displaystyle \eta }$естественный изоморфизм (или иногдаестественная эквивалентностьилиизоморфизм функторов). Два функтораиназываютсяестественно изоморфнымиили простоизоморфными,если существует естественный изоморфизм отдо. ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle F}$ ${\displaystyle G}$

Инфраестественное преобразование из в — это просто семейство морфизмов для всех в . Таким образом, естественное преобразование — это инфраестественное преобразование, для которого для любого морфизма . Натурализатор nat — это самая большая подкатегория , содержащая все объекты, для которых существует ограничение на естественное преобразование. ${\displaystyle \eta }$ ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle \eta _{X}:F(X)\to G(X)}$ ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle \eta _{Y}\circ F(f)=G(f)\circ \eta _{X}}$ ${\displaystyle f:X\to Y}$ ${\displaystyle \eta }$ ${\displaystyle (\eta )}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle \eta }$

Примеры

Противоположная группа

Такие заявления, как

«Каждая группа естественно изоморфна своей противоположной группе »

изобилуют современной математикой. Сейчас мы дадим точный смысл этого утверждения, а также его доказательство. Рассмотрим категорию всех групп с групповыми гомоморфизмами как морфизмы. Если группа, мы определяем ее противоположную группу следующим образом: это тот же набор, что и , а операция определяется . Таким образом , все умножения в «переворачиваются». Формирующая противоположная группа становится (ковариантным) функтором от до, если мы определим для любого группового гомоморфизма . Обратите внимание, что это действительно групповой гомоморфизм от до : ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle (G,*)}$ ${\displaystyle (G^{\text{op}},{*}^{\text{op}})}$ ${\displaystyle G^{\text{op}}}$ ${\displaystyle G}$ ${\displaystyle *^{\text{op}}}$ ${\displaystyle a*^{\text{op}}b=b*a}$ ${\displaystyle G^{\text{op}}}$ ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle f^{\text{op}}=f}$ ${\displaystyle f:G\to H}$ ${\displaystyle f^{\text{op}}}$ ${\displaystyle G^{\text{op}}}$ ${\displaystyle H^{\text{op}}}$

${\displaystyle f^{\text{op}}(a*^{\text{op}}b)=f(b*a)=f(b)*f(a)=f^{\text{op}}(a)*^{\text{op}}f^{\text{op}}(b).}$

Содержание вышеуказанного заявления следующее:

«Тождественный функтор естественно изоморфен противоположному функтору » ${\displaystyle {\text{Id}}_{\textbf {Grp}}:{\textbf {Grp}}\to {\textbf {Grp}}}$ ${\displaystyle {\text{op}}:{\textbf {Grp}}\to {\textbf {Grp}}}$

Чтобы доказать это, нам нужно предоставить изоморфизмы для каждой группы , такие, что приведенная выше диаграмма коммутирует. Набор . Формулы и показывают, что это гомоморфизм группы с обратным . Чтобы доказать естественность, мы начнем с группового гомоморфизма и покажем , т.е. для всех в . Это верно, поскольку и каждый гомоморфизм группы обладает свойством . ${\displaystyle \eta _{G}:G\to G^{\text{op}}}$ ${\displaystyle G}$ ${\displaystyle \eta _{G}(a)=a^{-1}}$ ${\displaystyle (a*b)^{-1}=b^{-1}*a^{-1}=a^{-1}*^{\text{op}}b^{-1}}$ ${\displaystyle (a^{-1})^{-1}=a}$ ${\displaystyle \eta _{G}}$ ${\displaystyle \eta _{G^{\text{op}}}}$ ${\displaystyle f:G\to H}$ ${\displaystyle \eta _{H}\circ f=f^{\text{op}}\circ \eta _{G}}$ ${\displaystyle (f(a))^{-1}=f^{\text{op}}(a^{-1})}$ ${\displaystyle a}$ ${\displaystyle G}$ ${\displaystyle f^{\text{op}}=f}$ ${\displaystyle (f(a))^{-1}=f(a^{-1})}$

Модули

Пусть – -модульный гомоморфизм правых модулей. Для каждого левого модуля существует естественное отображение , образующее естественное преобразование . Для каждого правого модуля существует естественное отображение, определяемое формулой , образующее естественное преобразование . ${\displaystyle \varphi :M\longrightarrow M^{\prime }}$ ${\displaystyle R}$ ${\displaystyle N}$ ${\displaystyle \varphi \otimes N:M\otimes _{R}N\longrightarrow M^{\prime }\otimes _{R}N}$ ${\displaystyle \eta :M\otimes _{R}-\implies M'\otimes _{R}-}$ ${\displaystyle N}$ ${\displaystyle \eta _{N}:{\text{Hom}}_{R}(M',N)\longrightarrow {\text{Hom}}_{R}(M,N)}$ ${\displaystyle \eta _{N}(f)=f\varphi }$ ${\displaystyle \eta :{\text{Hom}}_{R}(M',-)\implies {\text{Hom}}_{R}(M,-)}$

Абелианизация

Учитывая группу , мы можем определить ее абелианизацию . Пусть обозначает отображение проекции на смежные классы . Этот гомоморфизм «естественен в », т. е. определяет естественное преобразование, которое мы сейчас и проверим. Пусть будет группа. Для любого гомоморфизма мы имеем то, что содержится в ядре , потому что любой гомоморфизм в абелеву группу убивает коммутант. Затем учитываем , что касается единственного гомоморфизма . Это создает функтор и естественное преобразование, но не естественный изоморфизм, от тождественного функтора к . ${\displaystyle G}$ ${\displaystyle G^{\text{ab}}=G/}$ ${\displaystyle [G,G]}$ ${\displaystyle \pi _{G}:G\to G^{\text{ab}}}$ ${\displaystyle [G,G]}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle f:G\to H}$ ${\displaystyle [G,G]}$ ${\displaystyle \pi _{H}\circ f}$ ${\displaystyle \pi _{H}\circ f}$ ${\displaystyle G^{\text{ab}}}$ ${\displaystyle f^{\text{ab}}\circ \pi _{G}=\pi _{H}\circ f}$ ${\displaystyle f^{\text{ab}}:G^{\text{ab}}\to H^{\text{ab}}}$ ${\displaystyle {\text{ab}}:{\textbf {Grp}}\to {\textbf {Grp}}}$ ${\displaystyle \pi }$ ${\displaystyle {\text{ab}}}$

Гомоморфизм Гуревича

В алгебраической топологии изобилуют функторы и естественные преобразования , примерами которых служат гомоморфизмы Гуревича . Для любого точечного топологического пространства и натурального числа существует групповой гомоморфизм ${\displaystyle (X,x)}$ ${\displaystyle n}$

${\displaystyle h_{n}\colon \pi _{n}(X,x)\to H_{n}(X)}$

от -й группы гомотопий к -й группе гомологий . Оба и являются функторами из категории Top ^* точечных топологических пространств в категорию групп Grp и являются естественным преобразованием из в . ${\displaystyle n}$ ${\displaystyle (X,x)}$ ${\displaystyle n}$ ${\displaystyle X}$ ${\displaystyle \pi _{n}}$ ${\displaystyle H_{n}}$ ${\displaystyle h_{n}}$ ${\displaystyle \pi _{n}}$ ${\displaystyle H_{n}}$

Определитель

Учитывая коммутативные кольца и гомоморфизм колец , соответствующие группы обратимых матриц и наследуют гомоморфизм, который мы обозначаем через , полученный применением к каждому элементу матрицы. Аналогично, ограничивается гомоморфизмом группы , где обозначает группу единиц . Фактически и являются функторами из категории коммутативных колец в . Определитель группы , обозначаемый , является гомоморфизмом группы ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle f:R\to S}$ ${\displaystyle n\times n}$ ${\displaystyle {\text{GL}}_{n}(R)}$ ${\displaystyle {\text{GL}}_{n}(S)}$ ${\displaystyle {\text{GL}}_{n}(f)}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f^{*}:R^{*}\to S^{*}}$ ${\displaystyle R^{*}}$ ${\displaystyle R}$ ${\displaystyle {\text{GL}}_{n}}$ ${\displaystyle *}$ ${\displaystyle {\textbf {CRing}}}$ ${\displaystyle {\textbf {Grp}}}$ ${\displaystyle {\text{GL}}_{n}(R)}$ ${\displaystyle {\text{det}}_{R}}$

${\displaystyle {\mbox{det}}_{R}\colon {\mbox{GL}}_{n}(R)\to R^{*}}$

что естественно в : поскольку определитель определяется одной и той же формулой для каждого кольца, имеет место. Это делает определитель естественным преобразованием из в . ${\displaystyle R}$ ${\displaystyle f^{*}\circ {\text{det}}_{R}={\text{det}}_{S}\circ {\text{GL}}_{n}(f)}$ ${\displaystyle {\text{GL}}_{n}}$ ${\displaystyle *}$

Двойной двойник векторного пространства

Если задан эндофунктор, то есть функтор, который отображает категорию в эту же категорию, то происходит естественное преобразование тождественного функтора в этот функтор с компонентами . ${\displaystyle F}$ ${\displaystyle \alpha }$ ${\displaystyle \alpha _{C}=F(C)}$

Например, если поле , то для каждого векторного пространства над мы имеем «естественное» инъективное линейное отображение из векторного пространства в его двойное двойное поле . Эти отображения «естественны» в следующем смысле: двойная двойственная операция является функтором, а отображения — компонентами естественного преобразования от тождественного функтора к двойному двойственному функтору. ${\displaystyle K}$ ${\displaystyle V}$ ${\displaystyle K}$ ${\displaystyle V\to V^{**}}$

Конечное исчисление

Для каждой абелевой группы набор функций от целых чисел до базового набора формирует абелеву группу при поточечном добавлении. (Вот стандартный функтор забвения .) Учитывая морфизм , отображение , заданное левой композицией с элементами первого, само по себе является гомоморфизмом абелевых групп; таким образом мы получаем функтор . Конечно-разностный оператор, переводящий каждую функцию в, представляет собой отображение из в себя, и совокупность таких отображений дает естественное преобразование . ${\displaystyle G}$ ${\displaystyle {\text{Hom}}_{\textbf {Set}}(\mathbb {Z} ,U(G))}$ ${\displaystyle G}$ ${\displaystyle V_{\mathbb {Z} }(G)}$ ${\displaystyle U}$ ${\displaystyle U:{\textbf {Ab}}\to {\textbf {Set}}}$ ${\displaystyle {\textbf {Ab}}}$ ${\displaystyle \varphi :G\to G'}$ ${\displaystyle V_{\mathbb {Z} }(\varphi ):V_{\mathbb {Z} }(G)\to V_{\mathbb {Z} }(G')}$ ${\displaystyle \varphi }$ ${\displaystyle V_{\mathbb {Z} }:{\textbf {Ab}}\to {\textbf {Ab}}}$ ${\displaystyle \Delta _{G}}$ ${\displaystyle f:\mathbb {Z} \to U(G)}$ ${\displaystyle \Delta (f):n\mapsto f(n+1)-f(n)}$ ${\displaystyle V_{\mathbb {Z} }(G)}$ ${\displaystyle \Delta }$ ${\displaystyle \Delta :V_{\mathbb {Z} }\to V_{\mathbb {Z} }}$

Присоединение Тензор-хом

Рассмотрим категорию ${\displaystyle {\textbf {Ab}}}$ абелевых групп и групповых гомоморфизмов. Для всех абелевых групп и мы имеем групповой изоморфизм ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Z}$

${\displaystyle {\text{Hom}}(X\otimes Y,Z)\to {\text{Hom}}(X,{\text{Hom}}(Y,Z))}$.

Эти изоморфизмы «естественны» в том смысле, что они определяют естественное преобразование между двумя задействованными функторами . (Здесь «op» — категория , противоположная , не путать с тривиальным функтором противоположной группы  !) ${\displaystyle {\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}^{\text{op}}\times {\textbf {Ab}}\to {\textbf {Ab}}}$ ${\displaystyle {\textbf {Ab}}}$ ${\displaystyle {\textbf {Ab}}}$

Формально это соединение тензор-хом и является архетипическим примером пары сопряженных функторов . Естественные преобразования часто возникают в сочетании с присоединенными функторами, и действительно, присоединенные функторы определяются некоторым естественным изоморфизмом. Кроме того, каждая пара сопряженных функторов снабжена двумя естественными преобразованиями (обычно не изоморфизмами), называемыми единицей и коюнитом .

Неестественный изоморфизм

Понятие естественного преобразования является категориальным и утверждает (неформально), что конкретное отображение между функторами может быть выполнено последовательно во всей категории. Неформально, конкретное отображение (особенно изоморфизм) между отдельными объектами (не целыми категориями) называется «естественным изоморфизмом», что неявно означает, что оно фактически определено для всей категории и определяет естественное преобразование функторов; формализация этой интуиции стала мотивирующим фактором в развитии теории категорий. И наоборот, конкретное отображение между конкретными объектами можно назвать неестественным изоморфизмом (или «этот изоморфизм не является естественным»), если отображение не может быть расширено до естественного преобразования во всей категории. Учитывая объект , функтор (приняв для простоты первый функтор за единицу) и доказательство неестественности изоморфизма легче всего показать, задав автоморфизм , который не коммутирует с этим изоморфизмом (так что ). Более строго, если кто-то желает доказать, что и не являются естественно изоморфными, без ссылки на конкретный изоморфизм, для этого необходимо показать, что для любого изоморфизма существует такой, с которым он не коммутирует; в некоторых случаях один автоморфизм работает для всех возможных изоморфизмов, тогда как в других случаях нужно показать, как построить разные автоморфизмы для каждого изоморфизма. Карты категорий играют решающую роль: любое инфраестественное преобразование является естественным, если, например, единственными картами являются карта идентичности. ${\displaystyle X,}$ ${\displaystyle G}$ ${\displaystyle \eta \colon X\to G(X),}$ ${\displaystyle A\colon X\to X}$ ${\displaystyle \eta \circ A\neq G(A)\circ \eta }$ ${\displaystyle X}$ ${\displaystyle G(X)}$ ${\displaystyle \eta }$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \eta }$ ${\displaystyle A_{\eta }}$

Это похоже (но более категорично) на концепции теории групп или теории модулей, где данное разложение объекта в прямую сумму «не естественно» или, скорее, «не уникально», поскольку существуют автоморфизмы, которые не сохраняют прямую сумму. разложение суммы - см., например, Структурную теорему для конечно порожденных модулей в области главных идеалов § Уникальность .

Некоторые авторы различают обозначения, используя для естественного изоморфизма и для неестественного изоморфизма, сохраняя равенство (обычно равенство отображений). ${\displaystyle \cong }$ ${\displaystyle \approx }$ ${\displaystyle =}$

Пример: фундаментальная группа тора

В качестве примера различия между функториальным утверждением и отдельными объектами рассмотрим гомотопические группы пространства произведений, в частности фундаментальную группу тора.

Гомотопические группы пространства продукта естественным образом являются продуктом гомотопических групп компонентов с изоморфизмом, заданным проекцией на два фактора, в основном потому, что отображения в пространство продукта являются в точности произведениями отображений на компоненты - это функториал заявление. ${\displaystyle \pi _{n}((X,x_{0})\times (Y,y_{0}))\cong \pi _{n}((X,x_{0}))\times \pi _{n}((Y,y_{0})),}$

Однако тор (который абстрактно является произведением двух окружностей) имеет фундаментальную группу, изоморфную , но расщепление не является естественным. Обратите внимание на использование , и : ^[a] ${\displaystyle Z^{2}}$ ${\displaystyle \pi _{1}(T,t_{0})\approx \mathbf {Z} \times \mathbf {Z} }$ ${\displaystyle \approx }$ ${\displaystyle \cong }$ ${\displaystyle =}$

${\displaystyle \pi _{1}(T,t_{0})\approx \pi _{1}(S^{1},x_{0})\times \pi _{1}(S^{1},y_{0})\cong \mathbf {Z} \times \mathbf {Z} =\mathbf {Z} ^{2}.}$

Этот абстрактный изоморфизм с произведением не является естественным, поскольку некоторые изоморфизмы не сохраняют произведение: самогомеоморфизм (мыслимый как фактор-пространство ) заданный (геометрически поворот Дена вокруг одной из порождающих кривых) действует как этот матрица на (она входит в общую линейную группу обратимых целочисленных матриц), которая не сохраняет разложение как произведение, поскольку она не диагональна. Однако если тор дан как произведение (что эквивалентно разложению пространства), то расщепление группы следует из общего утверждения, сделанного ранее. В категориальном плане соответствующей категорией (сохраняющей структуру пространства продукта) являются «карты пространств продукта, а именно пара карт между соответствующими компонентами». ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle R^{2}/\mathbb {Z} ^{2}}$ ${\displaystyle \left({\begin{smallmatrix}1&1\\0&1\end{smallmatrix}}\right)}$ ${\displaystyle \mathbb {Z} ^{2}}$ ${\displaystyle {\text{GL}}(\mathbb {Z} ,2)}$ ${\displaystyle (T,t_{0})=(S^{1},x_{0})\times (S^{1},y_{0})}$

Естественность является категоричным понятием и требует очень точного определения того, какие именно данные даны: тор как пространство, которое оказывается продуктом (в категории пространств и непрерывных отображений), отличается от тора, представленного как продукт (в категории пространств и непрерывных отображений). категория произведений двух пространств и непрерывные отображения между соответствующими компонентами).

Пример: двойственное конечномерному векторному пространству.

Каждое конечномерное векторное пространство изоморфно своему двойственному пространству, но между этими двумя пространствами может существовать множество различных изоморфизмов. В общем случае не существует естественного изоморфизма между конечномерным векторным пространством и двойственным к нему пространством. ^[1] Однако родственные категории (с дополнительной структурой и ограничениями на карты) имеют естественный изоморфизм, как описано ниже.

Двойственное пространство конечномерного векторного пространства снова является конечномерным векторным пространством той же размерности, и, таким образом, они изоморфны, поскольку размерность является единственным инвариантом конечномерных векторных пространств над данным полем. Однако в отсутствие дополнительных ограничений (например, требования, чтобы карты сохраняли выбранный базис) отображение пространства в двойственное ему не является уникальным, и, следовательно, такой изоморфизм требует выбора и не является «естественным». В категории конечномерных векторных пространств и линейных отображений можно определить инфраестественный изоморфизм векторных пространств к их двойственным, выбрав изоморфизм для каждого пространства (скажем, выбрав базис для каждого векторного пространства и взяв соответствующий изоморфизм), но это не будет определять естественную трансформацию. Интуитивно это происходит потому, что это требует выбора, строго потому, что любой такой выбор изоморфизмов не будет коммутировать, скажем, с нулевым отображением; подробное обсуждение см. (Mac Lane & Birkhoff 1999, §VI.4).

Начиная с конечномерных векторных пространств (как объектов), а также тождественных и двойственных функторов, можно определить естественный изоморфизм, но для этого необходимо сначала добавить дополнительную структуру, а затем ограничить карты от «всех линейных карт» до «линейных карт, которые соблюдают это состав". Явно, для каждого векторного пространства требуется, чтобы оно содержало данные изоморфизма его двойственному пространству . Другими словами, в качестве объектов возьмем векторные пространства с невырожденной билинейной формой . Это определяет инфраестественный изоморфизм (изоморфизм для каждого объекта). Затем ограничиваются отображения только теми отображениями, которые коммутируют с изоморфизмами: или, другими словами, сохраняют билинейную форму: . (Эти карты определяют натурализатор изоморфизмов.) Полученная категория с объектами, конечномерными векторными пространствами с невырожденной билинейной формой, и линейными преобразованиями отображений, соблюдающими билинейную форму, по построению имеет естественный изоморфизм от единицы к двойственной форме. (каждое пространство имеет изоморфизм своему двойственному пространству, и отображения в категории должны коммутировать). С этой точки зрения эта конструкция (добавление преобразований для каждого объекта, ограничение коммутации карт с ними) является совершенно общей и не зависит от каких-либо конкретных свойств векторных пространств. ${\displaystyle \eta _{V}\colon V\to V^{*}}$ ${\displaystyle b_{V}\colon V\times V\to K}$ ${\displaystyle T\colon V\to U}$ ${\displaystyle T^{*}(\eta _{U}(T(v)))=\eta _{V}(v)}$ ${\displaystyle b_{U}(T(v),T(w))=b_{V}(v,w)}$

В этой категории (конечномерные векторные пространства с невырожденной билинейной формой, линейные преобразования карт, соблюдающие билинейную форму) двойственное отображение между векторными пространствами можно идентифицировать как транспонирование . Часто по причинам геометрического интереса это специализировано на подкатегорию, требуя, чтобы невырожденные билинейные формы имели дополнительные свойства, такие как симметричность ( ортогональные матрицы ), симметричность и положительно определенная ( пространство внутреннего продукта ), симметричная полуторалинейная ( эрмитово пространство ), кососимметричное и полностью изотропное ( симплектическое векторное пространство ) и т. д. – во всех этих категориях векторное пространство естественно отождествляется со своим двойственным, по невырожденной билинейной форме.

Операции с естественными преобразованиями

Горизонтальная и вертикальная композиция природных преобразований

Вертикальная композиция

Если и являются естественными преобразованиями между функторами , то мы можем скомпоновать их, чтобы получить естественное преобразование . Это делается покомпонентно: ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \epsilon :G\Rightarrow H}$ ${\displaystyle F,G,H:C\to D}$ ${\displaystyle \epsilon \circ \eta :F\Rightarrow H}$

${\displaystyle (\epsilon \circ \eta )_{X}=\epsilon _{X}\circ \eta _{X}}$.

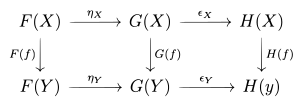
Эта вертикальная композиция естественных преобразований ассоциативна и имеет тождество и позволяет рассматривать саму совокупность всех функторов как категорию (см. ниже в разделе «Категории функторов»). Тождественное естественное преобразование на функторе имеет компоненты . ^[2] ${\displaystyle C\to D}$ ${\displaystyle \mathrm {id} _{F}}$ ${\displaystyle F}$ ${\displaystyle (\mathrm {id} _{F})_{X}=\mathrm {id} _{F(X)}}$

Для , . ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \mathrm {id} _{G}\circ \eta =\eta =\eta \circ \mathrm {id} _{F}}$

Горизонтальная композиция

Если — естественное преобразование между функторами и — естественное преобразование между функторами , то композиция функторов допускает композицию естественных преобразований с компонентами ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle F,G:C\to D}$ ${\displaystyle \epsilon :J\Rightarrow K}$ ${\displaystyle J,K:D\to E}$ ${\displaystyle \epsilon *\eta :J\circ F\Rightarrow K\circ G}$

${\displaystyle (\epsilon *\eta )_{X}=\epsilon _{G(X)}\circ J(\eta _{X})=K(\eta _{X})\circ \epsilon _{F(X)}}$.

Используя усы (см. ниже), мы можем написать

${\displaystyle (\epsilon *\eta )_{X}=(\epsilon G)_{X}\circ (J\eta )_{X}=(K\eta )_{X}\circ (\epsilon F)_{X}}$,

следовательно

${\displaystyle \epsilon *\eta =\epsilon G\circ J\eta =K\eta \circ \epsilon F}$.

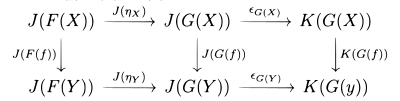
Эта горизонтальная композиция естественных преобразований также ассоциативна с идентичностью. Это тождество является тождественным естественным преобразованием тождественного функтора , т.е. естественным преобразованием, которое связывает с каждым объектом его тождественный морфизм : для объекта в категории , . ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle (\mathrm {id} _{\mathrm {id} _{C}})_{X}=\mathrm {id} _{\mathrm {id} _{C}(X)}=\mathrm {id} _{X}}$

Для с , . ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle F,G:C\to D}$ ${\displaystyle \mathrm {id} _{\mathrm {id} _{D}}*\eta =\eta =\eta *\mathrm {id} _{\mathrm {id} _{C}}}$

Поскольку тождественные функторы и являются функторами, тождество горизонтальной композиции является также тождеством вертикальной композиции, но не наоборот. ^[3] ${\displaystyle \mathrm {id} _{C}}$ ${\displaystyle \mathrm {id} _{D}}$

бакенбарды

Усы — это внешняя бинарная операция между функтором и естественным преобразованием. ^{[4] [5]}

Если – естественное преобразование между функторами и – другой функтор, то мы можем сформировать естественное преобразование, определив ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle F,G:C\to D}$ ${\displaystyle H:D\to E}$ ${\displaystyle H\eta :H\circ F\Rightarrow H\circ G}$

${\displaystyle (H\eta )_{X}=H(\eta _{X})}$.

Если, с другой стороны , это функтор, естественное преобразование определяется формулой ${\displaystyle K:B\to C}$ ${\displaystyle \eta K:F\circ K\Rightarrow G\circ K}$

${\displaystyle (\eta K)_{X}=\eta _{K(X)}}$.

Это также горизонтальная композиция, в которой одним из естественных преобразований является естественная трансформация идентичности:

${\displaystyle H\eta =\mathrm {id} _{H}*\eta }$и . ${\displaystyle \eta K=\eta *\mathrm {id} _{K}}$

Обратите внимание, что (соответственно ) обычно не является левой (соответственно правой) идентичностью горизонтальной композиции ( и вообще), за исключением случаев, когда (соответственно ) является тождественным функтором категории (соответственно ). ${\displaystyle \mathrm {id} _{H}}$ ${\displaystyle \mathrm {id} _{K}}$ ${\displaystyle *}$ ${\displaystyle H\eta \neq \eta }$ ${\displaystyle \eta K\neq \eta }$ ${\displaystyle H}$ ${\displaystyle K}$ ${\displaystyle D}$ ${\displaystyle C}$

Закон об обмене

Эти две операции связаны тождеством, которое заменяет вертикальную композицию горизонтальной композицией: если у нас есть четыре естественных преобразования, как показано на изображении справа, то выполняется следующее тождество: ${\displaystyle \alpha ,\alpha ',\beta ,\beta '}$

${\displaystyle (\beta '\circ \alpha ')*(\beta \circ \alpha )=(\beta '*\beta )\circ (\alpha '*\alpha )}$.

Вертикальные и горизонтальные композиции также связаны естественными трансформациями идентичности:

для и , . ^[6] ${\displaystyle F:C\to D}$ ${\displaystyle G:D\to E}$ ${\displaystyle \mathrm {id} _{G}*\mathrm {id} _{F}=\mathrm {id} _{G\circ F}}$

Поскольку усы представляют собой горизонтальную композицию с тождеством, закон обмена сразу дает компактные формулы горизонтальной композиции без необходимости анализа компонентов и коммутативной диаграммы: ${\displaystyle \eta :F\Rightarrow G}$ ${\displaystyle \epsilon :J\Rightarrow K}$

${\displaystyle {\begin{aligned}\epsilon *\eta &=(\epsilon \circ \mathrm {id} _{J})*(\mathrm {id} _{G}\circ \eta )=(\epsilon *\mathrm {id} _{G})\circ (\mathrm {id} _{J}*\eta )=\epsilon G\circ J\eta \\&=(\mathrm {id} _{K}\circ \epsilon )*(\eta \circ \mathrm {id} _{F})=(\mathrm {id} _{K}*\eta )\circ (\epsilon *\mathrm {id} _{F})=K\eta \circ \epsilon F\end{aligned}}}$.

Категории функторов

Если это любая категория и небольшая категория , мы можем сформировать категорию функторов , имеющую в качестве объектов все функторы из до и морфизмы - естественные преобразования между этими функторами. Это образует категорию, поскольку для любого функтора существует тождественное естественное преобразование (которое присваивает каждому объекту тождественный морфизм на ), а композиция двух естественных преобразований («вертикальная композиция» выше) снова является естественным преобразованием. ${\displaystyle C}$ ${\displaystyle I}$ ${\displaystyle C^{I}}$ ${\displaystyle I}$ ${\displaystyle C}$ ${\displaystyle F}$ ${\displaystyle 1_{F}:F\to F}$ ${\displaystyle X}$ ${\displaystyle F(X)}$

Изоморфизмы в являются в точности естественными изоморфизмами. То есть естественное преобразование является естественным изоморфизмом тогда и только тогда, когда существует естественное преобразование такое, что и . ${\displaystyle C^{I}}$ ${\displaystyle \eta :F\to G}$ ${\displaystyle \epsilon :G\to F}$ ${\displaystyle \eta \epsilon =1_{G}}$ ${\displaystyle \epsilon \eta =1_{F}}$

Категория функтора особенно полезна, если она возникает из ориентированного графа . Например, если категория ориентированного графа • → • , то имеет в качестве объектов морфизмы , а морфизм между и в является парой морфизмов и в таких, что «квадрат коммутирует», т.е. ${\displaystyle C^{I}}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle C^{I}}$ ${\displaystyle C}$ ${\displaystyle \phi :U\to V}$ ${\displaystyle \psi :X\to Y}$ ${\displaystyle C^{I}}$ ${\displaystyle f:U\to X}$ ${\displaystyle g:V\to Y}$ ${\displaystyle C}$ ${\displaystyle \psi \circ f=g\circ \phi }$

В более общем смысле можно построить 2-категорию , чья ${\displaystyle {\textbf {Cat}}}$

• 0-ячейки (объекты) — это небольшие категории,
• 1-клетки (стрелки) между двумя объектами и являются функторами от до , ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle C}$ ${\displaystyle D}$
• 2-ячейки между двумя 1-ячейками (функторами) и являются естественными преобразованиями из в . ${\displaystyle F:C\to D}$ ${\displaystyle G:C\to D}$ ${\displaystyle F}$ ${\displaystyle G}$

Горизонтальные и вертикальные композиции представляют собой композиции между естественными преобразованиями, описанными ранее. Тогда категория функтора является просто hom-категорией в этой категории (оставляя в стороне вопросы малости). ${\displaystyle C^{I}}$

Больше примеров

Каждый предел и копредел служат примером простого естественного преобразования, поскольку конус представляет собой естественное преобразование с диагональным функтором в качестве области определения. Действительно, если пределы и копределы определяются непосредственно в терминах их универсального свойства , они являются универсальными морфизмами в категории функтора.

Лемма Йонеды

Если — объект локально малой категории , то присваивание определяет ковариантный функтор . Этот функтор называется представимым (в более общем плане представимый функтор — это любой функтор, естественно изоморфный этому функтору при соответствующем выборе ). Естественные преобразования представимого функтора в произвольный функтор вполне известны и легко описываются; таково содержание леммы Йонеды . ${\displaystyle X}$ ${\displaystyle C}$ ${\displaystyle Y\mapsto {\text{Hom}}_{C}(X,Y)}$ ${\displaystyle F_{X}:C\to {\textbf {Set}}}$ ${\displaystyle X}$ ${\displaystyle F:C\to {\textbf {Set}}}$

Исторические заметки

Говорят, что Сондерс Мак Лейн , один из основателей теории категорий, заметил: «Я изобрел категории не для изучения функторов; я изобрел их для изучения естественных преобразований». ^[7] Как изучение групп не является полным без изучения гомоморфизмов , так и изучение категорий не является полным без изучения функторов . Причина комментария Мак Лейна в том, что изучение функторов само по себе не является полным без изучения естественных преобразований.

Контекстом замечания Мак Лейна была аксиоматическая теория гомологии . Можно показать, что различные способы построения гомологии совпадают: например, в случае симплициального комплекса группы, определенные непосредственно, будут изоморфны группам сингулярной теории. Что невозможно легко выразить без языка естественных преобразований, так это то, как группы гомологии совместимы с морфизмами между объектами и как две эквивалентные теории гомологии не только имеют одни и те же группы гомологии, но также и одни и те же морфизмы между этими группами.

Смотрите также

• Математический портал

• Сверхъестественная трансформация
• Универсальная собственность
• Теория высших категорий

Примечания

1. Z ⁿ можно определить как n -кратное произведение Z или как произведение Z ^{n  − 1} и Z , которые являются слегка разными множествами (хотя их можно естественным образом идентифицировать, что будет обозначено как ≅). Здесь мы зафиксировали определения, и в любом случае они совпадают при n  = 2.

Рекомендации

1. (Мак Лейн и Биркгоф 1999, §VI.4)
2. «Естественное преобразование идентичности в nLab» .
3. «Естественные преобразования». 7 апреля 2015 г.
4. "Определение: Усы - ProofWiki" .
5. "Усы в nLab" .
6. https://arxiv.org/pdf/1612.09375v1.pdf, с. 38
7. (Мак Лейн 1998, §I.4)

• Мак Лейн, Сондерс (1998), Категории для работающего математика , Тексты для выпускников по математике 5 (2-е изд.), Springer-Verlag, стр. 16, ISBN 0-387-98403-8
• Мак Лейн, Сондерс ; Биркгоф, Гарретт (1999), Алгебра (3-е изд.), AMS Chelsea Publishing, ISBN 0-8218-1646-2.
• Аводи, Стив (2010). Теория категорий . Оксфорд, Нью-Йорк: Издательство Оксфордского университета. п. 156. ИСБН 978-0199237180.
• Лейн, Сондерс (1992). Пучки в геометрии и логике: первое введение в теорию топоса . Нью-Йорк: Springer-Verlag. п. 13. ISBN 0387977104.

Внешние ссылки

• nLab, вики-проект по математике, физике и философии с упором на n -категориальную точку зрения.
• Дж. Адамек, Х. Херрлих, Г. Стрекер, Абстрактные и конкретные категории – радость кошек
• Стэнфордская энциклопедия философии : «Теория категорий» Жан-Пьера Маркиза. Обширная библиография.
• Баэз, Джон, 1996, «Повесть о n-категориях». Неофициальное введение в более высокие категории.