Закон Рэлея-Джинса

Приближение спектральной яркости абсолютно черного тела

Сравнение закона Рэлея–Джинса с приближением Вина и законом Планка для тела с температурой 5800 К.

В физике закон Рэлея -Джинса является приближением к спектральной яркости электромагнитного излучения как функции длины волны от черного тела при заданной температуре посредством классических аргументов. Для длины волны λ это где - спектральная яркость (мощность, излучаемая на единицу излучающей площади, на стерадиан , на единицу длины волны), - скорость света , - постоянная Больцмана , а - температура в кельвинах . Для частоты выражение вместо этого $${\displaystyle B_{\lambda }(T)={\frac {2ck_{\text{B}}T}{\lambda ^{4}}},}$$ ${\displaystyle B_{\lambda }}$ ${\displaystyle c}$ ${\displaystyle k_{\text{B}}}$ ${\displaystyle T}$ ${\displaystyle \nu }$ $${\displaystyle B_{\nu }(T)={\frac {2\nu ^{2}k_{\text{B}}T}{c^{2}}}.}$$

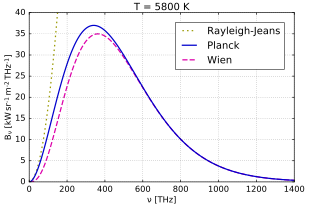
Закон Рэлея-Джинса согласуется с экспериментальными результатами на больших длинах волн (низкие частоты), но сильно расходится на коротких длинах волн (высокие частоты). Это несоответствие между наблюдениями и предсказаниями классической физики обычно известно как ультрафиолетовая катастрофа . ^{[1] [2]} Закон Планка , который дает правильное излучение на всех частотах, имеет закон Рэлея-Джинса в качестве своего низкочастотного предела.

Историческое развитие

В 1900 году британский физик лорд Рэлей вывел зависимость λ ⁻⁴ закона Рэлея–Джинса на основе классических физических аргументов, опираясь на теорему о равнораспределении . Этот закон предсказывал выход энергии, который расходится к бесконечности , когда длина волны стремится к нулю (когда частота стремится к бесконечности). Измерения спектрального излучения реальных черных тел показали, что излучение согласуется с расчетом Рэлея на низких частотах, но расходится на высоких частотах, достигая максимума и затем падая с частотой, поэтому полная излучаемая энергия конечна. Рэлей осознал нефизическое поведение своей формулы на высоких частотах и ​​ввел специальное ограничение, чтобы исправить его, но экспериментаторы обнаружили, что его ограничение не согласуется с данными. ^{[1] [3]} Хендрик Лоренц также представил вывод зависимости от длины волны в 1903 году. Более полные выводы, которые включали константу пропорциональности, были представлены в 1905 году Рэлеем и сэром Джеймсом Джинсом и независимо Альбертом Эйнштейном . ^[3] Рэлей считал, что это несоответствие можно разрешить, если теорема о равнораспределении окажется недействительной для высокочастотных колебаний, в то время как Джинс утверждал, что основной причиной является отсутствие теплового равновесия между материей и светоносным эфиром . ^[3]

Рэлей опубликовал свой первый вывод частотной зависимости в июне 1900 года. Планк открыл кривую, теперь известную как закон Планка, в октябре того же года и представил ее в декабре. ^[3] Первоначальное намерение Планка состояло в том, чтобы найти удовлетворительный вывод выражения Вина для кривой излучения черного тела, который точно описывал бы данные на высоких частотах. Планк нашел первоначальный вывод Вина неадекватным и разработал свой собственный. Затем, узнав, что самые последние экспериментальные результаты не согласуются с его предсказаниями для низких частот, Планк пересмотрел свои вычисления, получив то, что теперь называется законом Планка. ^[4]

Сравнение с законом Планка

В 1900 году Макс Планк эмпирически получил выражение для излучения черного тела, выраженное через длину волны λ = c / ν ( закон Планка ): где h — постоянная Планка , а k _B — постоянная Больцмана . Закон Планка не страдает от ультрафиолетовой катастрофы и хорошо согласуется с экспериментальными данными, но его полное значение (которое в конечном итоге привело к квантовой теории) было оценено только несколько лет спустя. С тех пор в пределе высоких температур или больших длин волн член в экспоненте становится малым, и экспонента хорошо аппроксимируется членом первого порядка полинома Тейлора : $${\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}},}$$ $${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots ,}$$ $${\displaystyle e^{\frac {hc}{\lambda k_{\text{B}}T}}\approx 1+{\frac {hc}{\lambda k_{\text{B}}T}}.}$$

Так $${\displaystyle {\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {1}{\frac {hc}{\lambda k_{\text{B}}T}}}={\frac {\lambda k_{\text{B}}T}{hc}}.}$$

Это приводит к формуле Планка для черного тела , которая сводится к классическому выражению Рэлея–Джинса. $${\displaystyle B_{\lambda }(T)={\frac {2ck_{\text{B}}T}{\lambda ^{4}}},}$$

Тот же аргумент можно применить к излучению черного тела, выраженному в терминах частоты ν = c / λ . В пределе малых частот, то есть , ${\displaystyle h\nu \ll k_{\text{B}}T}$ $${\displaystyle B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {2h\nu ^{3}}{c^{2}}}\cdot {\frac {k_{\text{B}}T}{h\nu }}={\frac {2\nu ^{2}k_{\mathrm {B} }T}{c^{2}}}.}$$

Последнее выражение представляет собой закон Рэлея–Джинса в пределе малых частот.

Согласованность выражений, зависящих от частоты и длины волны

При сравнении частотно- и длинноволновых зависимостей закона Рэлея-Джинса важно помнить, что и Обратите внимание, что эти два выражения имеют разные единицы измерения, поскольку шаг длины волны не эквивалентен шагу частоты. Поэтому, даже после подстановки значения , поскольку имеет единицы энергии, излучаемой в единицу времени на единицу площади излучающей поверхности, на единицу телесного угла, на единицу длины волны , тогда как имеет единицы энергии, излучаемой в единицу времени на единицу площади излучающей поверхности, на единицу телесного угла, на единицу частоты . Чтобы быть последовательными, мы должны использовать равенство , где обе стороны теперь имеют единицы мощности (энергии, излучаемой в единицу времени) на единицу площади излучающей поверхности, на единицу телесного угла. $${\displaystyle {\frac {dP}{d\lambda }}=B_{\lambda }(T)}$$ $${\displaystyle {\frac {dP}{d\nu }}=B_{\nu }(T).}$$ ${\displaystyle d\lambda }$ ${\displaystyle d\nu }$ $${\displaystyle B_{\lambda }(T)\neq B_{\nu }(T),}$$ ${\displaystyle \lambda =c/\nu }$ ${\displaystyle B_{\lambda }(T)}$ ${\displaystyle B_{\nu }(T)}$ $${\displaystyle B_{\lambda }\,d\lambda =dP=B_{\nu }\,d\nu ,}$$

Исходя из закона Рэлея-Джинса в терминах длины волны, получаем, что Это приводит к $${\displaystyle B_{\lambda }(T)=B_{\nu }(T){\frac {d\nu }{d\lambda }},}$$ $${\displaystyle {\frac {d\nu }{d\lambda }}={\frac {d}{d\lambda }}\left({\frac {c}{\lambda }}\right)=-{\frac {c}{\lambda ^{2}}}.}$$ $${\displaystyle B_{\lambda }(T)={\frac {2k_{\text{B}}T\left({\frac {c}{\lambda }}\right)^{2}}{c^{2}}}\times {\frac {c}{\lambda ^{2}}}={\frac {2ck_{\text{B}}T}{\lambda ^{4}}}.}$$

Другие формы закона Рэлея-Джинса

В зависимости от приложения функция Планка может быть выражена в 3 различных формах. Первая включает энергию, излучаемую в единицу времени на единицу площади излучающей поверхности, на единицу телесного угла, на спектральную единицу. В этой форме функция Планка и связанные с ней пределы Рэлея-Джинса задаются как или $${\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {2ck_{\text{B}}T}{\lambda ^{4}}}}$$ $${\displaystyle B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {2k_{\text{B}}T\nu ^{2}}{c^{2}}}.}$$

Альтернативно, закон Планка может быть записан как выражение для излучаемой мощности, интегрированной по всем телесным углам. В этой форме функция Планка и связанные с ней пределы Рэлея-Джинса задаются как или ${\displaystyle I(\nu ,T)=\pi B_{\nu }(T)}$ $${\displaystyle I(\lambda ,T)={\frac {2\pi hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {2\pi ck_{\text{B}}T}{\lambda ^{4}}}}$$ $${\displaystyle I(\nu ,T)={\frac {2\pi h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {2\pi k_{\text{B}}T\nu ^{2}}{c^{2}}}.}$$

В других случаях закон Планка записывается как для энергии на единицу объема (плотность энергии). В этой форме функция Планка и связанные с ней пределы Рэлея-Джинса задаются как или ${\textstyle u(\nu ,T)={\frac {4\pi }{c}}B_{\nu }(T)}$ $${\displaystyle u(\lambda ,T)={\frac {8\pi hc}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\text{B}}T}}-1}}\approx {\frac {8\pi k_{\text{B}}T}{\lambda ^{4}}}}$$ $${\displaystyle u(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{e^{\frac {h\nu }{k_{\text{B}}T}}-1}}\approx {\frac {8\pi k_{\text{B}}T\nu ^{2}}{c^{3}}}.}$$

Смотрите также

• Закон Стефана-Больцмана
• Закон смещения Вина
• приближение Вина
• Уравнение Сакумы–Хаттори

Ссылки

1. Kutner, Mark L. (2003). Астрономия: Физическая перспектива. Cambridge University Press. стр. 15. ISBN 0-521-52927-1.
2. Рыбицки; Лайтман (2004). Радиационные процессы в астрофизике . Wiley. стр. 20–28. ISBN 0-471-82759-2.
3. Pais, A. (1979-10-01). "Эйнштейн и квантовая теория". Reviews of Modern Physics . 51 (4): 863–914. Bibcode : 1979RvMP...51..863P. doi : 10.1103/RevModPhys.51.863. ISSN  0034-6861.
4. Краг, Х. (2000). «Макс Планк: неохотный революционер». Physics World . 13 (12): 31–36. doi :10.1088/2058-7058/13/12/34.

Внешние ссылки

• Вывод закона Рэлея-Джинса
• Вывод мод волны в кубе