Закон Снеллиуса

Формула для углов преломления

Преломление света на границе двух сред с разными показателями преломления , при этом n ₂ > n _1. Поскольку во второй среде скорость меньше (v ₂ < v ₁ ), угол преломления θ ₂ меньше угла падения θ ₁ ; то есть луч в среде с большим показателем преломления находится ближе к нормали.

Закон Снеллиуса (также известный как закон Снеллиуса–Декарта , закон Ибн-Саля , ^[1] и закон преломления ) — это формула, используемая для описания соотношения между углами падения и преломления , когда речь идет о световых или других волнах, проходящих через границу между двумя различными изотропными средами , такими как вода, стекло или воздух. В оптике закон используется при трассировке лучей для вычисления углов падения или преломления, а в экспериментальной оптике — для нахождения показателя преломления материала. Закон также выполняется в метаматериалах , которые позволяют свету изгибаться «назад» под отрицательным углом преломления с отрицательным показателем преломления .

Закон гласит, что для данной пары сред отношение синусов угла падения ( ) и угла преломления ( ) равно показателю преломления второй среды относительно первой ( ), который равен отношению показателей преломления ( ) двух сред или, что эквивалентно, отношению фазовых скоростей ( ) в двух средах. ^[2] ${\displaystyle \theta _{1}}$ ${\displaystyle \theta _{2}}$ ${\displaystyle n_{21}}$ ${\displaystyle {\tfrac {n_{2}}{n_{1}}}}$ ${\displaystyle {\tfrac {v_{1}}{v_{2}}}}$

${\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}=n_{21}={\frac {n_{2}}{n_{1}}}={\frac {v_{1}}{v_{2}}}}$

Закон следует из принципа наименьшего времени Ферма , который, в свою очередь, следует из распространения света в виде волн.

История

Репродукция страницы рукописи Ибн Сахля , демонстрирующей его открытие закона преломления.

Птолемей в Александрии , Египет, ^[3] нашел соотношение, касающееся углов преломления, но оно было неточным для углов, которые не были малыми. Птолемей был уверен, что он нашел точный эмпирический закон, частично в результате небольшого изменения своих данных, чтобы соответствовать теории (см.: смещение подтверждения ). ^[4]

Взгляд на историю «Закона синусов» в 1837 году ^[5]

Закон в конечном итоге был назван в честь Снеллиуса , хотя впервые он был открыт персидским ученым Ибн Сахлем при дворе в Багдаде в 984 году. ^{[6] [7] [8]} В рукописи «О зажигательных зеркалах и линзах » Сахль использовал закон для получения форм линз, которые фокусируют свет без геометрической аберрации . ^[9]

Альхазен в своей «Книге оптики» (1021) был близок к повторному открытию закона преломления, но не сделал этого шага. ^[10]

Закон был заново открыт Томасом Харриотом в 1602 году ^[11] , который, однако, не опубликовал свои результаты, хотя он переписывался с Кеплером по этому поводу. В 1621 году голландский астроном Виллеброрд Снеллиус (1580–1626) — Снелл — вывел математически эквивалентную форму, которая осталась неопубликованной при его жизни. Рене Декарт независимо вывел закон, используя эвристические аргументы сохранения импульса в терминах синусов в своем эссе 1637 года «Диоптрика» , и использовал его для решения ряда оптических задач. Отвергнув решение Декарта, Пьер де Ферма пришел к тому же решению, основанному исключительно на его принципе наименьшего времени . Декарт предположил, что скорость света бесконечна, однако при выводе закона Снеллиуса он также предположил, что чем плотнее среда, тем больше скорость света. Ферма поддерживал противоположные предположения, то есть, что скорость света конечна, и его вывод зависел от того, что скорость света меньше в более плотной среде. ^{[12] [13]} Вывод Ферма также использовал его изобретение равенства , математическую процедуру, эквивалентную дифференциальному исчислению, для нахождения максимумов, минимумов и касательных. ^{[14] [15]}

В своей влиятельной математической книге «Геометрия» Декарт решает задачу, над которой работали Аполлоний Пергский и Папп Александрийский . Даны n прямых L и точка P(L) на каждой прямой, найдите геометрическое место точек Q, такое, что длины отрезков QP(L) удовлетворяют определенным условиям. Например, когда n = 4, даны прямые a, b, c и d и точка A на a, B на b и т. д., найдите геометрическое место точек Q, такое, что произведение QA*QB равно произведению QC*QD. Когда не все прямые параллельны, Папп показал, что геометрические места являются коническими, но когда Декарт рассматривал большие n, он получал кубические и более высокие степени кривых. Чтобы показать, что кубические кривые интересны, он показал, что они естественным образом возникли в оптике из закона Снеллиуса. ^[16]

Согласно Дейкстерхёйсу, ^[17] «В De natura lucis et proprietate (1662) Исаак Фоссиус сказал, что Декарт видел статью Снеллиуса и придумал свое собственное доказательство. Теперь мы знаем, что это обвинение незаслуженно, но с тех пор оно принималось много раз». И Ферма, и Гюйгенс повторяли это обвинение в том, что Декарт скопировал Снеллиуса. На французском языке закон Снеллиуса иногда называют «la loi de Descartes» или чаще « loi de Snell-Descartes ».

Строительство Христиана Гюйгенса

В своем «Трактате о свете» 1678 года Христиан Гюйгенс показал, как закон синусов Снеллиуса можно объяснить или вывести из волновой природы света, используя то, что мы стали называть принципом Гюйгенса-Френеля .

С развитием современной оптической и электромагнитной теории древний закон Снеллиуса был выведен на новый уровень. В 1962 году Николас Бломберген показал, что на границе нелинейной среды закон Снеллиуса следует записать в общем виде. ^[18] В 2008 и 2011 годах также было продемонстрировано, что плазмонные метаповерхности изменяют направления отражения и преломления светового луча. ^{[19] [20]}

Объяснение

Закон Снеллиуса на стене в Лейдене

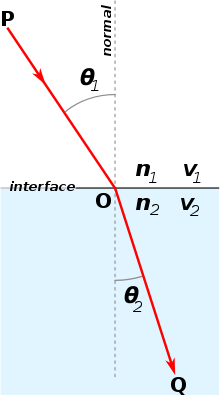
Закон Снеллиуса используется для определения направления световых лучей через преломляющие среды с различными показателями преломления. Показатели преломления среды, обозначенные , и т. д., используются для представления коэффициента, на который уменьшается скорость светового луча при прохождении через преломляющую среду, такую ​​как стекло или вода, по сравнению с его скоростью в вакууме. ${\displaystyle n_{1}}$ ${\displaystyle n_{2}}$

При прохождении света через границу между средами, в зависимости от относительных показателей преломления двух сред, свет будет преломляться либо на меньший угол, либо на больший. Эти углы измеряются относительно нормальной линии , представленной перпендикулярно границе. В случае света, перемещающегося из воздуха в воду, свет будет преломляться в направлении нормальной линии, поскольку свет замедляется в воде; свет, перемещающийся из воды в воздух, будет преломляться в сторону от нормальной линии.

Преломление между двумя поверхностями также называют обратимым, поскольку, если бы все условия были идентичны, углы были бы такими же для света, распространяющегося в противоположном направлении.

Закон Снеллиуса обычно справедлив только для изотропных или зеркальных сред (таких как стекло ). В анизотропных средах, таких как некоторые кристаллы , двойное лучепреломление может расщепить преломленный луч на два луча: обыкновенный или o -луч, который следует закону Снеллиуса, и другой необыкновенный или e -луч, который может не быть копланарным с падающим лучом.

Когда свет или другая волна являются монохроматическими, то есть имеют одну частоту, закон Снеллиуса можно также выразить через отношение длин волн в двух средах : ${\displaystyle \lambda _{1}}$ ${\displaystyle \lambda _{2}}$

${\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {\lambda _{1}}{\lambda _{2}}}}$

Выводы и формулы

Волновые фронты от точечного источника в контексте закона Снеллиуса. Область под серой линией имеет более высокий показатель преломления и пропорционально более низкую скорость света , чем область над ней.

Закон Снеллиуса можно вывести различными способами.

Вывод из принципа Ферма

Закон Снеллиуса можно вывести из принципа Ферма , который гласит, что свет проходит путь, который занимает наименьшее время. Взяв производную от оптической длины пути , можно найти стационарную точку , которая дает путь, пройденный светом. (Существуют ситуации, когда свет нарушает принцип Ферма, не проходя путь с наименьшим временем, как при отражении в (сферическом) зеркале.) В классической аналогии область с меньшим показателем преломления заменяется пляжем, область с большим показателем преломления — морем, и самый быстрый способ для спасателя на пляже добраться до тонущего в море человека — бежать по пути, который следует закону Снеллиуса.

Свет из среды 1, точки Q, попадает в среду 2, происходит преломление, и, наконец, свет достигает точки P.

Как показано на рисунке справа, предположим, что показатели преломления среды 1 и среды 2 равны и соответственно. Свет входит в среду 2 из среды 1 через точку O. ${\displaystyle n_{1}}$ ${\displaystyle n_{2}}$

${\displaystyle \theta _{1}}$- угол падения, - угол преломления относительно нормали. ${\displaystyle \theta _{2}}$

Фазовые скорости света в среде 1 и среде 2 равны

${\displaystyle v_{1}=c/n_{1}}$и

${\displaystyle v_{2}=c/n_{2}}$соответственно.

${\displaystyle c}$ скорость света в вакууме.

Пусть T — время, необходимое свету для прохождения пути из точки Q через точку O в точку P.

${\displaystyle T={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+(l-x)^{2}}}{v_{2}}}={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+l^{2}-2lx+x^{2}}}{v_{2}}}}$

где a, b, l и x обозначены на правом рисунке, причем x — изменяющийся параметр.

Чтобы минимизировать это, можно дифференцировать:

${\displaystyle {\frac {dT}{dx}}={\frac {x}{v_{1}{\sqrt {x^{2}+a^{2}}}}}+{\frac {-(l-x)}{v_{2}{\sqrt {(l-x)^{2}+b^{2}}}}}=0}$(стационарная точка)

Обратите внимание, что ${\displaystyle {\frac {x}{\sqrt {x^{2}+a^{2}}}}=\sin \theta _{1}}$

и ${\displaystyle {\frac {l-x}{\sqrt {(l-x)^{2}+b^{2}}}}=\sin \theta _{2}}$

Поэтому,

${\displaystyle {\frac {dT}{dx}}={\frac {\sin \theta _{1}}{v_{1}}}-{\frac {\sin \theta _{2}}{v_{2}}}=0}$

${\displaystyle {\frac {\sin \theta _{1}}{v_{1}}}={\frac {\sin \theta _{2}}{v_{2}}}}$

${\displaystyle {\frac {n_{1}\sin \theta _{1}}{c}}={\frac {n_{2}\sin \theta _{2}}{c}}}$

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}}$

Вывод из принципа Гюйгенса

В качестве альтернативы закон Снеллиуса можно вывести с использованием интерференции всех возможных путей световой волны от источника до наблюдателя — это приводит к деструктивной интерференции везде, за исключением экстремумов фазы (где интерференция конструктивна), которые становятся фактическими путями.

Вывод из уравнений Максвелла

Другой способ вывода закона Снеллиуса заключается в применении общих граничных условий уравнений Максвелла для электромагнитного излучения и индукции .

Вывод из закона сохранения энергии и импульса

Еще один способ вывода закона Снеллиуса основан на соображениях трансляционной симметрии. ^[21] Например, однородная поверхность, перпендикулярная направлению z, не может изменить поперечный импульс. Поскольку вектор распространения пропорционален импульсу фотона, поперечное направление распространения должно оставаться одинаковым в обеих областях. Предположим без потери общности плоскость падения в плоскости . Используя хорошо известную зависимость волнового числа от показателя преломления среды, мы немедленно выводим закон Снеллиуса. ${\displaystyle {\vec {k}}}$ ${\displaystyle (k_{x},k_{y},0)}$ ${\displaystyle z,x}$ ${\displaystyle k_{x{\text{Region}}_{1}}=k_{x{\text{Region}}_{2}}}$

${\displaystyle k_{x{\text{Region}}_{1}}=k_{x{\text{Region}}_{2}}\,}$

${\displaystyle n_{1}k_{0}\sin \theta _{1}=n_{2}k_{0}\sin \theta _{2}\,}$

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\,}$

где — волновое число в вакууме. Хотя ни одна поверхность не является по-настоящему однородной в атомном масштабе, полная трансляционная симметрия является прекрасным приближением, когда область однородна в масштабе длины волны света. ${\displaystyle k_{0}={\frac {2\pi }{\lambda _{0}}}={\frac {\omega }{c}}}$

Векторная форма

Имея нормализованный вектор света (направленный от источника света к поверхности) и нормализованный вектор нормали плоскости , можно вычислить нормализованные отраженные и преломленные лучи через косинусы угла падения и угла преломления , без явного использования значений синуса или каких-либо тригонометрических функций или углов: ^[22] ${\displaystyle {\vec {l}}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle \theta _{1}}$ ${\displaystyle \theta _{2}}$

${\displaystyle \cos \theta _{1}=-{\vec {n}}\cdot {\vec {l}}}$

Примечание: должно быть положительным, что и будет, если — нормальный вектор, указывающий от поверхности в сторону, откуда падает свет, область с индексом . Если отрицательно, то указывает в сторону без света, поэтому начните заново, заменив его на отрицательный. ${\displaystyle \cos \theta _{1}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle n_{1}}$ ${\displaystyle \cos \theta _{1}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle {\vec {n}}}$

${\displaystyle {\vec {v}}_{\mathrm {reflect} }={\vec {l}}+2\cos \theta _{1}{\vec {n}}}$

Этот отраженный вектор направления указывает обратно на ту сторону поверхности, откуда пришел свет.

Теперь применим закон Снеллиуса к отношению синусов, чтобы вывести формулу для вектора направления преломленного луча:

${\displaystyle \sin \theta _{2}=\left({\frac {n_{1}}{n_{2}}}\right)\sin \theta _{1}=\left({\frac {n_{1}}{n_{2}}}\right){\sqrt {1-\left(\cos \theta _{1}\right)^{2}}}}$

${\displaystyle \cos \theta _{2}={\sqrt {1-(\sin \theta _{2})^{2}}}={\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\left(1-\left(\cos \theta _{1}\right)^{2}\right)}}}$

${\displaystyle {\vec {v}}_{\mathrm {refract} }=\left({\frac {n_{1}}{n_{2}}}\right){\vec {l}}+\left({\frac {n_{1}}{n_{2}}}\cos \theta _{1}-\cos \theta _{2}\right){\vec {n}}}$

Формула может показаться проще с точки зрения переименованных простых значений и избегания любого появления имен тригонометрических функций или имен углов: ${\displaystyle r=n_{1}/n_{2}}$ ${\displaystyle c=-{\vec {n}}\cdot {\vec {l}}}$

${\displaystyle {\vec {v}}_{\mathrm {refract} }=r{\vec {l}}+\left(rc-{\sqrt {1-r^{2}\left(1-c^{2}\right)}}\right){\vec {n}}}$

Пример:

${\displaystyle {\vec {l}}=\{0.707107,-0.707107\},~{\vec {n}}=\{0,1\},~r={\frac {n_{1}}{n_{2}}}=0.9}$

${\displaystyle c=\cos \theta _{1}=0.707107,~{\sqrt {1-r^{2}\left(1-c^{2}\right)}}=\cos \theta _{2}=0.771362}$

${\displaystyle {\vec {v}}_{\mathrm {reflect} }=\{0.707107,0.707107\},~{\vec {v}}_{\mathrm {refract} }=\{0.636396,-0.771362\}}$

Значения косинуса можно сохранить и использовать в уравнениях Френеля для расчета интенсивности результирующих лучей.

Полное внутреннее отражение обозначается отрицательным подкоренным выражением в уравнении для , что может произойти только для лучей, пересекающих менее плотную среду ( ). ${\displaystyle \cos \theta _{2}}$ ${\displaystyle n_{2}<n_{1}}$

Полное внутреннее отражение и критический угол

Демонстрация отсутствия преломления при углах, больших критического угла

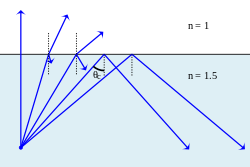
Когда свет распространяется из среды с более высоким показателем преломления в среду с более низким показателем преломления, закон Снеллиуса, по-видимому, требует в некоторых случаях (когда угол падения достаточно велик), чтобы синус угла преломления был больше единицы. Это, конечно, невозможно, и свет в таких случаях полностью отражается границей, явление, известное как полное внутреннее отражение . Наибольший возможный угол падения, который все еще приводит к преломленному лучу, называется критическим углом ; в этом случае преломленный луч распространяется вдоль границы между двумя средами.

Преломление света на границе раздела двух сред

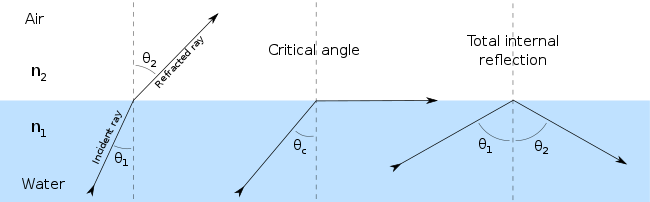
Например, рассмотрим луч света, движущийся из воды в воздух с углом падения 50°. Показатели преломления воды и воздуха приблизительно равны 1,333 и 1 соответственно, поэтому закон Снеллиуса дает нам соотношение

${\displaystyle \sin \theta _{2}={\frac {n_{1}}{n_{2}}}\sin \theta _{1}={\frac {1.333}{1}}\cdot \sin \left(50^{\circ }\right)=1.333\cdot 0.766=1.021,}$

что невозможно удовлетворить. Критический угол θ _крит — это значение θ ₁ , для которого θ ₂ равен 90°:

${\displaystyle \theta _{\text{crit}}=\arcsin \left({\frac {n_{2}}{n_{1}}}\sin \theta _{2}\right)=\arcsin {\frac {n_{2}}{n_{1}}}=48.6^{\circ }.}$

Дисперсия

Во многих средах распространения волн скорость волны изменяется в зависимости от частоты или длины волны; это справедливо для распространения света в большинстве прозрачных веществ, кроме вакуума. Эти среды называются дисперсионными. В результате углы, определяемые законом Снеллиуса, также зависят от частоты или длины волны, так что луч смешанных длин волн, такой как белый свет, будет распространяться или рассеиваться. Такое рассеивание света в стекле или воде лежит в основе происхождения радуг и других оптических явлений , в которых разные длины волн проявляются как разные цвета.

В оптических приборах дисперсия приводит к хроматической аберрации ; размытости, зависящей от цвета, которая иногда является эффектом, ограничивающим разрешение. Это было особенно актуально в рефракционных телескопах до изобретения ахроматических объективов.

Среды с потерями, поглощающие или проводящие

В проводящей среде диэлектрическая проницаемость и показатель преломления являются комплексными величинами. Следовательно, таковыми являются угол преломления и волновой вектор. Это означает, что, в то время как поверхности постоянной действительной фазы являются плоскостями, нормали которых составляют угол, равный углу преломления с нормалью к интерфейсу, поверхности постоянной амплитуды, напротив, являются плоскостями, параллельными самому интерфейсу. Поскольку эти две плоскости в общем случае не совпадают друг с другом, волна называется неоднородной. ^[23] Преломленная волна экспоненциально затухает, причем показатель пропорционален мнимой составляющей показателя преломления. ^{[24] [25]}

Смотрите также

• Кривая брахистохроны  – Самый быстрый спуск по кривой без трения для простого доказательства Якоба Бернулли
• Вариационное исчисление  – Дифференциальное исчисление на функциональных пространствах
• Расчет затухания радиоволн в атмосфере
• Затухающая волна  – тип поля, в котором чистый поток электромагнитной энергии равен нулю.Pages displaying short descriptions of redirect targets
• Гамильтонова оптика
• Список показателей преломления
• Уравнение интерферометрии N-щели
• Отражение (физика)  – «отражение» волн от границы раздела.
• Окно Снеллиуса  – Подводное явление, обусловленное законом Снеллиуса.
• Показатель преломления в зависимости от длины волны света  – Эмпирическая связь между показателем преломления и длиной волны

Ссылки

1. * Будриуа, Аззедин; Рашед, Рошди; Лакшминараянан, Васудеван (2017-08-15). Наука, основанная на свете: технологии и устойчивое развитие, наследие Ибн аль-Хайтама. CRC Press. стр. 207. ISBN 978-1-351-65112-7.
   * Яо, X. Стив; Чэнь, Сяоцзюнь (Джеймс) (2022). Измерение и управление поляризацией в волоконно-оптических системах связи и датчиках. John Wiley & Sons. стр. 4. ISBN 978-1-119-75850-1.
   * Вольф, КБ; Кроцш, Г (1995-01-01). «Геометрия и динамика в преломляющих системах». European Journal of Physics . 16 (1): 14–20. Bibcode : 1995EJPh...16...14W. doi : 10.1088/0143-0807/16/1/003. ISSN  0143-0807.
   * Вольф, Курт Бернардо (2004-07-21). Геометрическая оптика на фазовом пространстве. Springer Science & Business Media. ISBN 978-3-540-22039-8.
2. Борн и Вольф (1959). Принципы оптики . Нью-Йорк, Нью-Йорк: Pergamon Press INC. стр. 37.
3. Дэвид Майкл Харланд (2007). " Кассини у Сатурна: результаты Гюйгенса ". стр. 1. ISBN 0-387-26129-X 
4. "Птолемей (ок. 100-ок. 170)". Мир научной биографии Эрика Вайнштейна .
5. Уильям Уэвелл, История индуктивной науки с древнейших времен до наших дней , Лондон: Джон Х. Паркер, 1837.
6. Пападопулос, Атанас (2017). «Рошди Рашед, историк греческой и арабской математики». HAL Open Science . стр. 12. hal-01653436.
7. Мурад Згал; Хамид-Эддин Буали; Зохра Бен Лахдар; Хабиб Хамам. «Первые шаги в изучении оптики: работы Ибн Сахля, Аль-Хайтама и Янга по преломлению как типичные примеры» (PDF) . Р. Рашед приписал Ибн Сахлю открытие закона преломления [23], обычно называемого законом Снеллиуса, а также законом Снеллиуса и Декарта.
8. Смит, А. Марк (2015). От зрения к свету: переход от древней к современной оптике. Издательство Чикагского университета. стр. 178. ISBN 978-0-226-17476-1.
9. Рашед, Рошди (1990). «Пионер в анакластике: Ибн Сахл о сжигании зеркал и линз». Isis . 81 (3): 464–491. doi :10.1086/355456. S2CID  144361526.^{[ спорный – обсудить ] [ требуется разъяснение ]}
10. AI Sabra (1981), Теории света от Декарта до Ньютона , Cambridge University Press . ( ср. Pavlos Mihas, Использование истории в разработке идей преломления, линз и радуги, стр. 5, Университет Демокрита, Фракия , Греция .)
11. Кван, А.; Дадли, Дж.; Ланц, Э. (2002). «Кто на самом деле открыл закон Снеллиуса?». Physics World . 15 (4): 64. doi :10.1088/2058-7058/15/4/44.
12. Флориан Каджори , История физики в ее элементарных разделах: включая эволюцию физических лабораторий (1922)
13. Фердинанд Розенбергер, Geschichte der Physik (1882), часть. II, стр.114
14. Карл Бенджамин Бойер , Радуга: от мифа к математике (1959)
15. Флориан Каджори , «Кто был первым изобретателем исчисления» The American Mathematical Monthly (1919) Vol.26
16. Геометрия Рене Декарта (Dover Books on Mathematics) Рене Декарта, Дэвида Юджина Смита и Марсии Л. Лэтэм (1 июня 1954 г.).
17. Дейкстерхейс, Фокко Ян (2004). Линзы и волны: Христиан Гюйгенс и математическая наука оптика в семнадцатом веке. Спрингер. ISBN 1-4020-2697-8.
18. Bloembergen, N.; Pershan, PS (1962). "Световые волны на границе нелинейных сред" (PDF) . Physical Review . 128 (2): 606. Bibcode :1962PhRv..128..606B. doi :10.1103/PhysRev.128.606. hdl :1874/7432. Архивировано (PDF) из оригинала 2022-10-09.
19. Xu, T.; et al. (2008). "Плазмонный дефлектор". Opt. Express . 16 (7): 4753–9. Bibcode : 2008OExpr..16.4753X. doi : 10.1364/oe.16.004753 . PMID  18542573.
20. Юй, Нанфан; Дженевет, Патрис; Кац, Михаил А.; Айета, Франческо; Тетьен, Жан-Филипп; Капассо, Федерико; Габурро, Зено (октябрь 2011 г.). «Распространение света с фазовыми разрывами: обобщенные законы отражения и преломления». Science . 334 (6054): 333–7. Bibcode :2011Sci...334..333Y. doi : 10.1126/science.1210713 . PMID  21885733. S2CID  10156200.
21. Joannopoulos, John D; Johnson, SG; Winn, JN; Meade, RD (2008). Фотонные кристаллы: Формирование потока света (2-е изд.). Princeton NJ: Princeton University Press. стр. 31. ISBN 978-0-691-12456-8.
22. Гласснер, Эндрю С. (1989). Введение в трассировку лучей. Морган Кауфманн. ISBN 0-12-286160-4.
23. Борн и Вольф, раздел 13.2, «Преломление и отражение на металлической поверхности»
24. Хехт, Оптика , раздел 4.8, Оптические свойства металлов.
25. SJ Orfanidis, Электромагнитные волны и антенны , раздел 7.9, Наклонное падение на среду с потерями, [1] Архивировано 30 июля 2020 г. на Wayback Machine

Внешние ссылки

• Закон Ибн Сахля и Снелла Архивировано 2016-10-23 в Wayback Machine
• Открытие закона преломления
• Закон преломления Снеллиуса (волновые фронты) Тодда Роуленда, проект Wolfram Demonstrations
• Закон Снелла на стене в центре Лейдена. Архивировано 27.04.2018 на Wayback Machine.
• Эффект береговой линии