Метод оплаты имиджа

Методика расчета классической электростатики

Метод зарядов изображений (также известный как метод изображений и метод зеркальных зарядов ) — основной инструмент решения задач в электростатике . Название происходит от замены некоторых элементов в исходной компоновке мнимыми зарядами, что повторяет граничные условия задачи (см. Граничные условия Дирихле или Краевые условия Неймана ).

Справедливость метода изображений зарядов опирается на следствие теоремы единственности , которая утверждает, что электрический потенциал в объеме V однозначно определяется, если заданы как плотность заряда во всей области, так и значение электрического потенциала на всех границах. . Альтернативно, применение этого следствия к дифференциальной форме закона Гаусса показывает, что в объеме V, окруженном проводниками и содержащем заданную плотность заряда ρ , электрическое поле однозначно определяется, если задан общий заряд на каждом проводнике. Обладая знаниями либо об электрическом потенциале, либо об электрическом поле и соответствующих граничных условиях, мы можем заменить рассматриваемое нами распределение заряда на конфигурацию, которую легче анализировать, при условии, что она удовлетворяет уравнению Пуассона в интересующей области и предполагает правильные значения на границах. ^[1]

Отражение в проводящей плоскости

Поле положительного заряда над плоской проводящей поверхностью, найденное методом изображений.

Метод изображений электрического дипольного момента в проводящей плоскости

Начисление баллов

Простейшим примером метода изображения заряда является точечный заряд с зарядом q , расположенный над бесконечной заземленной (т.е.: ) проводящей пластиной в плоскости xy . Чтобы упростить эту задачу, мы можем заменить пластинку эквипотенциала зарядом − q , расположенным в точке . Такое расположение будет создавать одно и то же электрическое поле в любой точке (т. е. над проводящей пластиной) и удовлетворяет граничному условию, согласно которому потенциал вдоль пластины должен быть равен нулю. Эта ситуация эквивалентна исходной схеме, поэтому теперь силу, действующую на реальный заряд, можно рассчитать с помощью закона Кулона между двумя точечными зарядами. ^[2] ${\displaystyle (0,0,a)}$ ${\displaystyle V=0}$ ${\displaystyle (0,0,-a)}$ ${\displaystyle z>0}$

Потенциал в любой точке пространства, обусловленный этими двумя точечными зарядами + q в + a и - q в - a на оси z , задается в цилиндрических координатах как

${\displaystyle V\left(\rho ,\varphi ,z\right)={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+\left(z-a\right)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+\left(z+a\right)^{2}}}}\right)\,}$

Таким образом, поверхностная плотность заряда на заземленной плоскости определяется выражением

${\displaystyle \sigma =-\varepsilon _{0}\left.{\frac {\partial V}{\partial z}}\right|_{z=0}={\frac {-qa}{2\pi \left(\rho ^{2}+a^{2}\right)^{3/2}}}}$

Кроме того, полный заряд, индуцированный на проводящей плоскости, будет интегралом от плотности заряда по всей плоскости, поэтому:

${\displaystyle {\begin{aligned}Q_{t}&=\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\theta \\[6pt]&={\frac {-qa}{2\pi }}\int _{0}^{2\pi }d\theta \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\right)^{3/2}}}\\[6pt]&=-q\end{aligned}}}$

Полный заряд, индуцированный на плоскости, оказывается просто − q . Это можно видеть и из закона Гаусса , если учесть, что дипольное поле убывает в кубе расстояния на больших расстояниях, и поэтому полный поток поля через бесконечно большую сферу обращается в нуль.

Поскольку электрические поля удовлетворяют принципу суперпозиции , проводящая плоскость под несколькими точечными зарядами может быть заменена зеркальными изображениями каждого из зарядов по отдельности, без каких-либо других модификаций.

Электрические дипольные моменты

Изображение электрического дипольного момента p at над бесконечной заземленной проводящей плоскостью в плоскости xy представляет собой дипольный момент at равной величины и направления, повернутый по азимуту на π. То есть дипольный момент с декартовой составляющей будет иметь в образе дипольный момент . На диполь действует сила в направлении z , определяемая выражением ${\displaystyle (0,0,a)}$ ${\displaystyle (0,0,-a)}$ ${\displaystyle (p\sin \theta \cos \phi ,p\sin \theta \sin \phi ,p\cos \theta )}$ ${\displaystyle (-p\sin \theta \cos \phi ,-p\sin \theta \sin \phi ,p\cos \theta )}$

${\displaystyle F=-{\frac {1}{4\pi \varepsilon _{0}}}{\frac {3p^{2}}{16a^{4}}}\left(1+\cos ^{2}\theta \right)}$

и крутящий момент в плоскости, перпендикулярной диполю и проводящей плоскости,

${\displaystyle \tau =-{\frac {1}{4\pi \varepsilon _{0}}}{\frac {p^{2}}{16a^{3}}}\sin 2\theta }$

Отражение в плоской границе раздела диэлектриков

Подобно проводящей плоскости, можно рассмотреть случай плоской границы раздела двух различных диэлектрических сред. Если точечный заряд поместить в диэлектрик, имеющий диэлектрическую проницаемость , то на границе раздела (с диэлектриком, имеющим диэлектрическую проницаемость ) образуется связанный поляризационный заряд. Можно показать, что результирующее электрическое поле внутри диэлектрика, содержащего частицу, изменяется таким образом, что его можно описать изображением заряда внутри другого диэлектрика. Однако внутри другого диэлектрика заряд изображения отсутствует. ^[3] ${\displaystyle q}$ ${\displaystyle \epsilon _{1}}$ ${\displaystyle \epsilon _{2}}$

В отличие от металла, заряд изображения не является точно противоположным реальному заряду: . Он может даже не иметь того же знака, если заряд помещен внутри более прочного диэлектрического материала (заряды отталкиваются от областей с более низкой диэлектрической проницаемостью). Это видно из формулы. ${\displaystyle q'}$ ${\textstyle q'={\frac {\varepsilon _{1}-\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}}q}$

Отражение в проводящей сфере

Схема , иллюстрирующая метод изображения для уравнения Лапласа для сферы радиуса R. Зеленая точка — это заряд q, лежащий внутри сферы на расстоянии p от начала координат, красная точка — изображение этой точки, имеющей заряд − qR / p , лежащей вне сферы на расстоянии R ² / p от начала координат. источник. Потенциал, создаваемый двумя зарядами, на поверхности сферы равен нулю.

Линии поля вне заземленной сферы для заряда, находящегося вне сферы.

Некоторые поверхности требуют бесконечной серии зарядов точечного изображения.

Начисление баллов

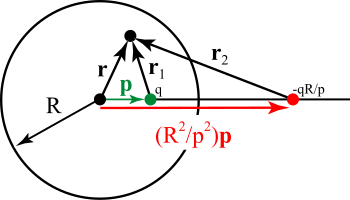
Метод изображений можно применить и к сфере. ^[4] Фактически случай изображений зарядов на плоскости является частным случаем случая изображений на сфере. Обращаясь к рисунку, мы хотим найти потенциал внутри заземленной сферы радиуса R с центром в начале координат, обусловленный точечным зарядом внутри сферы в заданном положении (В противоположном случае потенциал вне сферы из-за заряда снаружи сфере метод применяется аналогично). На рисунке это обозначено зеленой точкой. Пусть q — точечный заряд этой точки. Изображение этого заряда относительно заземленной сферы показано красным цветом. Он имеет заряд q ′ = −qR / p и лежит на линии, соединяющей центр сферы и внутренний заряд в позиции вектора . Видно, что потенциал в точке, заданной радиусом-вектором, обусловленный только обоими зарядами, определяется суммой потенциалов: ${\displaystyle \mathbf {p} }$ ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$ ${\displaystyle \mathbf {r} }$

${\displaystyle 4\pi \varepsilon _{0}V(\mathbf {r} )={\frac {q}{|\mathbf {r} _{1}|}}+{\frac {(-qR/p)}{|\mathbf {r} _{2}|}}={\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}+{\frac {(-qR/p)}{\sqrt {r^{2}+{\frac {R^{4}}{p^{2}}}-{\frac {2R^{2}}{p^{2}}}\mathbf {r} \cdot \mathbf {p} }}}}$

Умножение самого правого выражения дает:

${\displaystyle V(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\left[{\frac {q}{\sqrt {r^{2}+p^{2}-2\mathbf {r} \cdot \mathbf {p} }}}-{\frac {q}{\sqrt {{\frac {r^{2}p^{2}}{R^{2}}}+R^{2}-2\mathbf {r} \cdot \mathbf {p} }}}\right]}$

и видно, что на поверхности сферы (т. е. когда r = R ) потенциал исчезает. Таким образом, потенциал внутри сферы определяется приведенным выше выражением для потенциала двух зарядов. Этот потенциал не будет действовать вне сферы, поскольку заряд изображения на самом деле не существует, а скорее «заменяет» поверхностные плотности заряда, индуцированные на сфере внутренним зарядом при . Потенциал вне заземленной сферы будет определяться только распределением заряда вне сферы и не будет зависеть от распределения заряда внутри сферы. Если мы предположим для простоты (без ограничения общности), что внутренний заряд лежит на оси z, то плотность индуцированного заряда будет просто функцией полярного угла θ и определяется выражением: ${\displaystyle \mathbf {p} }$

${\displaystyle \sigma (\theta )=\varepsilon _{0}\left.{\frac {\partial V}{\partial r}}\right|_{r=R}={\frac {-q\left(R^{2}-p^{2}\right)}{4\pi R\left(R^{2}+p^{2}-2pR\cos \theta \right)^{3/2}}}}$

Полный заряд сферы можно найти путем интегрирования по всем углам:

${\displaystyle Q_{t}=\int _{0}^{\pi }d\theta \int _{0}^{2\pi }d\phi \,\,\sigma (\theta )R^{2}\sin \theta =-q}$

Заметим, что этим методом решается и обратная задача. Если у нас есть заряд q в векторной позиции вне заземленной сферы радиуса R , потенциал вне сферы определяется суммой потенциалов заряда и его образа заряда внутри сферы. Как и в первом случае, заряд изображения будет иметь заряд − qR / p и находиться в позиции вектора . Потенциал внутри сферы будет зависеть только от истинного распределения заряда внутри сферы. В отличие от первого случая интеграл будет иметь значение − qR / p . ${\displaystyle \mathbf {p} }$ ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$

Электрические дипольные моменты

Изображение электрического точечного диполя немного сложнее. Если диполь изображен как два больших заряда, разделенных небольшим расстоянием, то в изображении диполя будут изменены не только заряды с помощью описанной выше процедуры, но и расстояние между ними. Следуя описанной выше процедуре, обнаруживается, что диполь с дипольным моментом в позиции вектора , лежащей внутри сферы радиуса R, будет иметь изображение, расположенное в позиции вектора (т. е. то же самое, что и для простого заряда), и будет иметь простой заряд: ${\displaystyle M}$ ${\displaystyle \mathbf {p} }$ ${\displaystyle \left(R^{2}/p^{2}\right)\mathbf {p} }$

${\displaystyle q'={\frac {R\mathbf {p} \cdot \mathbf {M} }{p^{3}}}}$

и дипольный момент:

${\displaystyle \mathbf {M} '=\left({\frac {R}{p}}\right)^{3}\left[-\mathbf {M} +{\frac {2\mathbf {p} (\mathbf {p} \cdot \mathbf {M} )}{p^{2}}}\right]}$

Метод инверсии

Метод изображений сферы непосредственно приводит к методу инверсии. ^[5] Если мы имеем гармоническую функцию положения где – сферические координаты положения, то образ этой гармонической функции в сфере радиуса R относительно начала координат будет иметь вид ${\displaystyle \Phi (r,\theta ,\phi )}$ ${\displaystyle r,\theta ,\phi }$

${\displaystyle \Phi '(r,\theta ,\phi )={\frac {R}{r}}\,\Phi {\left({\frac {R^{2}}{r}},\theta ,\phi \right)}}$

Если потенциал возникает из набора зарядов определенной величины в определенных позициях , то потенциал изображения будет результатом серии зарядов определенной величины в определенных позициях . Отсюда следует, что если потенциал возникает из-за плотности заряда , то потенциал изображения будет результатом плотности заряда . ${\displaystyle \Phi }$ ${\displaystyle q_{i}}$ ${\displaystyle (r_{i},\theta _{i},\phi _{i})}$ ${\displaystyle Rq_{i}/r_{i}}$ ${\displaystyle (R^{2}/r_{i},\theta _{i},\phi _{i})}$ ${\displaystyle \Phi }$ ${\displaystyle \rho (r,\theta ,\phi )}$ ${\displaystyle \rho '(r,\theta ,\phi )=(R/r)\rho (R^{2}/r,\theta ,\phi )}$

Смотрите также

• Преобразование Кельвина
• Закон Кулона
• Теорема о дивергенции
• Поток
• Гауссова поверхность
• Принцип отражения Шварца
• Теорема единственности уравнения Пуассона
• Изображение антенны
• Принцип поверхностной эквивалентности

Рекомендации

Примечания

1. Гриффитс, Дэвид Дж. (2013). Введение в электродинамику (4-е изд.) . Пирсон . п. 121. ИСБН 978-0-321-85656-2.
2. Джинсы 1908, с. 186
3. Джексон 1962, с. 111
4. Тихонов, Андрей Н .; Самарский, Александр А. (1963). Уравнения математической физики. Нью-Йорк: Dover Publications . п. 354. ИСБН 0-486-66422-8.
5. Джексон 1962, с. 35

Источники

• Джексон, Джон Д. (1962). Классическая электродинамика. Джон Уайли и сыновья .
• Джинсы, Джеймс Х. (1908). Математическая теория электричества и магнетизма. Издательство Кембриджского университета .

дальнейшее чтение

• Фейнман, Ричард ; Лейтон, Роберт Б .; Сэндс, Мэтью (1989). Фейнмановские лекции по физике , главным образом по электромагнетизму и материи . Аддисон-Уэсли . ISBN 0-201-51003-0.
• Ландау, Лев Д. ; Лифшиц Евгений Михайлович ; Питаевский, Лев П. (1960). Электродинамика непрерывных сред, 2-е издание . Лондон: Эльзевир . ISBN 978-0-7506-2634-7.
• Перселл, Эдвард М. Курс физики Беркли, Том 2: Электричество и магнетизм (2-е изд.) . МакГроу-Хилл .