Правильный икосаэдр

Многогранник с 20 правильными треугольными гранями.

В геометрии правильный икосаэдр ^[1] (или просто икосаэдр ) — это выпуклый многогранник , который можно построить из пятиугольной антипризмы , прикрепив к каждой из его пятиугольных граней две пятиугольные пирамиды с правильными гранями или поместив точки на куб. Получившийся многогранник имеет 20 равносторонних треугольников в качестве граней, 30 ребер и 12 вершин. Это пример Платонова тела и дельтаэдра . Икосаэдрический граф представляет собой скелет правильного икосаэдра.

Многие многогранники построены из правильного икосаэдра. Например, большая часть многогранника Кеплера-Пуансо построена путем огранки . Некоторые из тел Джонсона можно построить, удалив пятиугольные пирамиды. Правильный икосаэдр имеет множество отношений с другими платоновыми телами, одним из которых является правильный додекаэдр как его двойственный многогранник , и он имеет историческую подоплеку сравнительного измерения. Он также имеет много связей с другими многогранниками .

Строительство

Правильный икосаэдр можно построить, как и другие гироудлиненные бипирамиды , начав с пятиугольной антипризмы , прикрепив к каждой из ее граней две пятиугольные пирамиды с правильными гранями . Эти пирамиды закрывают пятиугольные грани, заменяя их пятью равносторонними треугольниками , так что полученный многогранник имеет 20 равносторонних треугольников в качестве граней. ^[2] Этот процесс построения известен как гироудлинение , поэтому полученный многогранник также называют гировытянутой пятиугольной бипирамидой . ^{[ нужна цитата ]} .

Три взаимно перпендикулярных прямоугольника золотого сечения , ребра которых соединяют углы, образуют правильный икосаэдр.

Другой способ его построить — поставить две точки на каждой поверхности куба. На каждой грани нарисуйте отрезок между серединами двух противоположных ребер и найдите две точки на расстоянии золотого сечения от каждой средней точки. Эти двенадцать вершин описывают три взаимно перпендикулярные плоскости, между которыми проведены ребра. ^[3] Из-за приведенных выше конструкций правильный икосаэдр является платоновым телом , семейством многогранников с правильными гранями . Многогранник, гранями которого являются только равносторонние треугольники, называется дельтаэдром . Существует всего восемь различных выпуклых дельтаэдров, один из которых — правильный икосаэдр. ^[4]

Одна из возможных систем декартовых координат для вершин правильного икосаэдра, дающая длину ребра 2, следующая:

$${\displaystyle \left(0,\pm 1,\pm \varphi \right),\left(\pm 1,\pm \varphi ,0\right),\left(\pm \varphi ,0,\pm 1\right),}$$

золотое сечение^[5] ${\displaystyle \varphi =(1+{\sqrt {5}})/2}$

Характеристики

Измерение

3D модель правильного икосаэдра.

Внутренняя сфера выпуклого многогранника — это сфера внутри многогранника, касающаяся каждой его грани. Описанная сфера выпуклого многогранника — это сфера, содержащая многогранник и касающаяся каждого ребра. Средняя сфера выпуклого многогранника — это сфера, касающаяся каждого его ребра. Следовательно, учитывая, что длина ребра правильного икосаэдра, радиус внутренней сферы (внутренний радиус) , радиус описанной сферы (циркулярный радиус) и радиус средней сферы (мидрадиус) составляют соответственно: ^[6] ${\displaystyle a}$ ${\displaystyle r_{I}}$ ${\displaystyle r_{C}}$ ${\displaystyle r_{M}}$

$${\displaystyle r_{I}={\frac {\varphi ^{2}a}{2{\sqrt {3}}}}\approx 0.756a,\qquad r_{C}={\frac {\sqrt {\varphi ^{2}+1}}{2}}a\approx 0.951a,\qquad r_{M}={\frac {\varphi }{2}}a\approx 1.618a.}$$

Площадь поверхности многогранника равна сумме каждой его грани. Следовательно, площадь поверхности правильных икосаэдров в двадцать раз больше площади равностороннего треугольника. Объем правильного икосаэдра получается путем вычисления объема всех пирамид с учетом оснований треугольных граней и высоты с расстоянием от центроида треугольной грани до центра внутри правильного икосаэдра, радиуса описанной окружности правильного икосаэдра. ^[7] ${\displaystyle A}$ ${\displaystyle V}$

$${\displaystyle A=5{\sqrt {3}}a^{2}\approx 8.660a^{2},\qquad V={\frac {5\varphi ^{2}}{6}}a^{3}\approx 2.182a^{3}.}$$

ГеройПаппФибоначчи . ^[8] Аполлоний Пергский^[9]золотое сечение^[10][11]

Двугранный угол правильного икосаэдра можно вычислить, сложив угол пятиугольных пирамид с правильными гранями и пятиугольной антипризмы. Двугранный угол пятиугольной антипризмы и пятиугольной пирамиды между двумя соседними треугольными гранями составляет приблизительно . Двугранный угол пятиугольной антипризмы между пятиугольниками и треугольниками равен , а двугранный угол пятиугольной пирамиды между теми же гранями равен . Следовательно, для правильного икосаэдра двугранный угол между двумя соседними треугольниками на ребре, где прикреплены пятиугольная пирамида и пятиугольная антипризма, равен . ^[12] ${\displaystyle 138.2^{\circ }}$ ${\displaystyle 100.8^{\circ }}$ ${\displaystyle 37.4^{\circ }}$ ${\displaystyle 37.4^{\circ }+100.8^{\circ }=138.2^{\circ }}$

Симметрия

Полная икосаэдрическая симметрия имеет 15 зеркальных плоскостей (которые выглядят как большие голубые круги на этой сфере), встречающихся под порядковыми углами, разделяющих сферу на 120 фундаментальных треугольных областей . Есть 6 осей 5-го порядка (синие), 10 осей 3-го порядка (красные) и 15 осей 2-го порядка (пурпурные). Вершины правильного икосаэдра существуют в точках оси вращения 5-го порядка. ${\displaystyle \pi /5,\pi /3,\pi /2}$

Группа вращательной симметрии правильного икосаэдра изоморфна знакопеременной группе из пяти букв. Эта неабелева простая группа — единственная нетривиальная нормальная подгруппа симметрической группы из пяти букв. Поскольку группа Галуа общего уравнения пятой степени изоморфна симметрической группе из пяти букв, а эта нормальная подгруппа проста и неабелева, общее уравнение пятой степени не имеет решения в радикалах. Доказательство теоремы Абеля-Руффини использует этот простой факт, и Феликс Кляйн написал книгу, в которой использовалась теория икосаэдральных симметрий для получения аналитического решения общего уравнения пятой степени. ^[13]

Полная группа симметрии икосаэдра (включая отражения) известна как полная группа икосаэдра . Он изоморфен произведению группы вращательной симметрии и группы размера два, которая генерируется отражением через центр икосаэдра. ${\displaystyle C_{2}}$

Икосаэдрический граф

Икосаэдрический граф

Все графы Платона , включая икосаэдрические графы , являются многогранными графами . Это означает, что это плоские графы , графы, которые можно нарисовать на плоскости, не пересекая ее ребер; и они 3-вершинно связны , что означает, что удаление любых двух его вершин оставляет связный подграф. Согласно теореме Стейница , икосаэдрический граф, наделенный этими до сих пор свойствами, представляет собой скелет правильного икосаэдра. ^[14]

Икосаэдрический граф является гамильтоновым , что означает, что любая вершина, проходящая через другую, попадает на велосипедную дорожку ровно один раз. ^[15]

Связанные многогранники

В других Платоновых телах

Помимо сравнения размеров правильного икосаэдра и правильного додекаэдра, они двойственны друг другу. Икосаэдр можно вписать в додекаэдр, поместив его вершины в центры граней додекаэдра, и наоборот. ^[16]

Икосаэдр можно вписать в октаэдр , поместив его 12 вершин на 12 ребер октаэдра так, чтобы они делили каждое ребро на два золотых сечения . Поскольку золотые сечения неравны, существует пять различных способов сделать это последовательно, поэтому в каждый октаэдр можно вписать пять непересекающихся икосаэдров. ^[17]

Икосаэдр с длиной ребра можно вписать в куб с единичной длиной ребра, разместив шесть его ребер (3 ортогональные противоположные пары) на квадратных гранях куба, с центром в центрах граней и параллельно или перпендикулярно краям квадрата. ^[18] Поскольку ребер икосаэдра в пять раз больше, чем граней куба, существует пять способов сделать это последовательно, поэтому в каждый куб можно вписать пять непересекающихся икосаэдров. Длины ребер куба и вписанного икосаэдра находятся в золотом сечении . ^[19] ${\textstyle {\frac {1}{\varphi }}\approx 0.618}$

Звездчатость

Икосаэдр имеет большое количество звездочек . Коксетер и др. (1938) заявили, что для правильного икосаэдра было идентифицировано 59 звездочек. Первая форма — это сам икосаэдр. Один из них — правильный многогранник Кеплера–Пуансо . Три из них являются правильными составными многогранниками . ^[20]

Огранки

Большой додекаэдр , малый звездчатый додекаэдр и большой икосаэдр .

Малый звездчатый додекаэдр , большой додекаэдр и большой икосаэдр — это три грани правильного икосаэдра. Они имеют одинаковое расположение вершин . Все они имеют 30 ребер. Правильный икосаэдр и большой додекаэдр имеют одинаковое расположение ребер , но различаются гранями (треугольники и пятиугольники), как и малый звездчатый додекаэдр и большой икосаэдр (пентаграммы и треугольники).

Уменьшение

Тела Джонсона — это многогранники, все грани которых правильные, но не однородные. Это означает, что они не включают в себя архимедовы тела , каталонские тела , призмы и антипризмы . Некоторые из них построены с использованием удаления части правильного икосаэдра — процесса, известного как уменьшение . Это гироудлиненная пятиугольная пирамида , метабидиуменьшённый икосаэдр и трёхуменьшенный икосаэдр , которые удаляют одну, две и три пятиугольные пирамиды из икосаэдра соответственно. ^[21] У аналогичного рассеченного правильного икосаэдра две соседние вершины уменьшены, оставив две трапециевидные грани, а у бифастигия удалены 2 противоположных набора вершин и 4 трапециевидные грани.

Отношения с 600-клеточным и другими 4-многогранниками

Икосаэдр — это размерный аналог 600-ячеечного , правильного 4-мерного многогранника . 600-ячеечная имеет икосаэдрические сечения двух размеров, и каждая из ее 120 вершин представляет собой икосаэдрическую пирамиду ; икосаэдр — это вершина 600-ячеистой фигуры .

Ячейка с единичным радиусом 600 имеет тетраэдрические ячейки с длиной ребра , 20 из которых встречаются в каждой вершине, образуя икосаэдрическую пирамиду ( 4-пирамиду с икосаэдром в основании). Таким образом, 600-ячейка содержит 120 икосаэдров с длиной ребра . Ячейка с 600 ячейками также содержит кубы с единичной длиной ребра и октаэдры с единичной длиной ребра в качестве внутренних элементов , образованных ее хордами с единичной длиной . В 120-ячеечном единичном радиусе (еще один правильный 4-многогранник, который является одновременно двойственным 600-ячеечному и составным из 5 600-ячеечных) мы находим все три вида вписанных икосаэдров (в додекаэдре, в октаэдре, и в кубе). ${\textstyle {\frac {1}{\varphi }}\approx 0.618}$ ${\textstyle {\frac {1}{\varphi }}\approx 0.618}$

Полуправильный 4-многогранник, курносый 24-клеточный , имеет икосаэдрические ячейки.

Отношения с другими однородными многогранниками

Как уже упоминалось выше, правильный икосаэдр уникален среди платоновых тел , поскольку имеет двугранный угол примерно . Таким образом, подобно тому, как шестиугольники имеют углы не менее 120° и не могут использоваться в качестве граней выпуклого правильного многогранника, поскольку такая конструкция не удовлетворяет требованию, чтобы в вершине сходились хотя бы три грани и оставляли положительный дефект для складывания в В трех измерениях икосаэдры не могут использоваться в качестве ячеек выпуклого правильного многогранника , так как, аналогично, по крайней мере три ячейки должны пересекаться на ребре и оставлять положительный дефект для свертывания в четырех измерениях (вообще для выпуклого многогранника в n измерениях при по крайней мере три грани должны встретиться на вершине и оставить положительный дефект для сворачивания в n -пространстве). Однако в сочетании с подходящими ячейками, имеющими меньшие двугранные углы, икосаэдры можно использовать в качестве ячеек в полуправильных многогранниках (например, курносый 24-клеточный ), точно так же, как шестиугольники можно использовать в качестве граней в полуправильных многогранниках (например, в усеченный икосаэдр ). Наконец, к невыпуклым многогранникам не предъявляются такие же строгие требования, как к выпуклым многогранникам, и икосаэдры действительно являются ячейками икосаэдрического 120-клеточного , одного из десяти невыпуклых правильных многогранников . ${\displaystyle 138.19^{\circ }}$

Существуют искажения икосаэдра, которые, хотя и не являются правильными, но, тем не менее, являются однородными по вершинам . Они инвариантны относительно тех же вращений , что и тетраэдр, и в некоторой степени аналогичны курносому кубу и курносому додекаэдру , включая некоторые формы, которые являются киральными , а некоторые имеют T _h -симметрию, т.е. имеют плоскости симметрии, отличные от тетраэдра.

Связь с 6-кубом и ромбическим триаконтаэдром

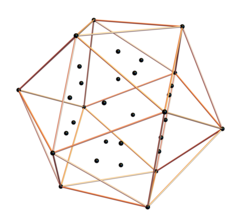
Икосаэдр можно спроецировать в 3D из 6D 6-демикуба , используя те же базисные векторы, которые образуют оболочку ромбического триаконтаэдра из 6-куба . Здесь показано, включая 20 внутренних вершин, которые не соединены 30 внешними ребрами оболочки стандартной длины 6D . Внутренние вершины образуют додекаэдр . ${\displaystyle {\sqrt {2}}}$

Используемые базисные векторы трехмерной проекции [u,v,w]:

$${\displaystyle {\begin{aligned}u&=(1,\varphi ,0,-1,\varphi ,0)\\v&=(\varphi ,0,1,\varphi ,0,-1)\\w&=(0,1,\varphi ,0,-1,\varphi )\\\end{aligned}}}$$

Приложения и его естественная форма

Игральные кости — это обычные объекты с разными многогранниками, один из них — правильный икосаэдр. Эти двадцатигранные игральные кости были найдены во многих древних временах. Одним из примеров являются игральные кости из «Птолемеев Египта», ^[22] которые позже были греческими буквами, начертанными на гранях в период Греции и Рима. ^[23] Другой пример был найден в сокровище Типу Султана , которое было сделано из золота и с цифрами, написанными на каждой стороне. ^[24] В некоторых ролевых играх , таких как Dungeons & Dragons , двадцатигранный кубик (обозначенный как d20 ) обычно используется для определения успеха или провала действия. Этот кубик имеет форму правильного икосаэдра. Он может быть пронумерован дважды от «0» до «9», и в этом виде он обычно служит десятигранным кубиком ( d10 ); большинство современных версий имеют маркировку от «1» до «20». ^[25] Scattergories — еще одна настольная игра, в которой игрок называет категории на карточке с заданным временем. Именование таких категорий изначально происходит по буквам, содержащимся в каждой двадцатигранной игральной кости. ^[26]

Правильный икосаэдр также может появляться во многих областях биологии. В вирусологии вирус герпеса имеет икосаэдрическую оболочку . Внешняя белковая оболочка ВИЧ заключена в правильный икосаэдр, как и головка типичного миовируса . ^[27] Несколько видов радиолярий, открытых Эрнстом Геккелем , описали свои раковины как различные правильные многогранники одинаковой формы; один из них — икосаэдры Циркогонии , скелет которых по форме напоминает правильный икосаэдр. ^[28]

Клозо - карбораны — химические соединения , форма которых очень близка к икосаэдру. Икосаэдрическое двойникование также встречается в кристаллах, особенно в наночастицах . Многие бориды и аллотропы бора содержат икосаэдр бора B ₁₂ в качестве основной структурной единицы.

Р. Бакминстер Фуллер и японский картограф Сёдзи Садао спроектировали карту мира в форме развернутого икосаэдра, названную проекцией Фуллера , максимальное искажение которой составляет всего 2%.

Примечания

1. См. произношение в Jones 2003: ( / ˌ aɪ k ɒ s ə ˈ h iː d r ən , - k ə -, - k oʊ -/ или / aɪ ˌ k ɒ s ə ˈ h iː d r ən / )
2. Сильвестр 2001, с. 140–141; Канди 1952 год.
3. Кромвель 1997, с. 70.
4. Шавинина 2013, с. 333; Канди 1952 год.
5. Стееб, Харди и Тански 2012, стр. 211.
6. Маклин 2007, с. 43–44; Коксетер 1973, Таблица I(i), стр. 292–293. См. столбец " ", где указаны обозначения Коксетера для среднего радиуса, также отметив, что Коксетер использует в качестве длины ребра (см. стр. 2). ${\displaystyle {}_{1}\!\mathrm {R} /\ell }$ ${\displaystyle {}_{1}\!\mathrm {R} }$ ${\displaystyle 2\ell }$
7. Маклин 2007, с. 43–44.
8. Герц-Фишлер 2013, с. 138–140.
9. Симмонс 2007, с. 50.
10. Саттон 2002, с. 55.
11. Числовые значения объемов вписанных Платоновых тел можно найти в Buker & Eggleton 1969.
12. Джонсон 1966, см. таблицу II, строка 4; Маклин 2007, с. 43–44.
13. Кляйн 1884. См. Симметрию икосаэдра: связанные геометрии для дальнейшей истории и связанные симметрии семи и одиннадцати букв.
14. Бикл 2020, с. 147.
15. Хопкинс 2004.
16. Херрманн и Салли 2013, с. 257.
17. Коксетер и др. 1938, с. 4; «Как тетраэдр можно вписать в куб, так и куб можно вписать в додекаэдр. Взаимно-поступательным движением это приводит к октаэдру, описанному вокруг икосаэдра. Каждая из двенадцати вершин икосаэдра делит ребро октаэдра согласно к " золотому сечению ". Учитывая икосаэдр, описанный октаэдр может быть выбран пятью способами, давая соединение пяти октаэдров , которое подпадает под наше определение звездчатого икосаэдра . (Обратное соединение пяти кубов, вершины которых принадлежат додекаэдр — это звездчатый триаконтаэдр .) Другой звездчатый икосаэдр можно сразу же вывести, превратив каждый октаэдр в звездчатую октангулу , образуя таким образом соединение десяти тетраэдров . Кроме того, мы можем выбрать по одному тетраэдру из каждой звездчатой ​​октангулы, чтобы получить соединение из пяти тетраэдров , который по-прежнему обладает всей вращательной симметрией икосаэдра (т.е. икосаэдрической группы ), хотя и потерял отражения.Отражая эту фигуру в любой плоскости симметрии икосаэдра, мы получаем дополнительный набор из пяти тетраэдров. Эти два набора из пяти тетраэдров энантиоморфны, то есть не конгруэнтны напрямую, а связаны, как пара обуви. [Такая] фигура, не имеющая плоскости симметрии (так что она энантиоморфна своему зеркальному изображению), называется киральной ».
18. Боровик 2006, стр. 8–9, §5. Как нарисовать икосаэдр на доске.
19. И наоборот, длина ребра куба, вписанного в додекаэдр, находится в золотом пропорции к длине ребра додекаэдра. Ребра куба лежат в пятиугольных гранях додекаэдра как правильные диагонали пятиугольника , которые всегда находятся в золотом сечении к ребру правильного пятиугольника. Когда куб вписан в додекаэдр, а в куб вписан икосаэдр, то додекаэдр и икосаэдр, не имеющие общих вершин, имеют одинаковую длину ребра.
20. Коксетер и др. 1938, с. 8–26.
21. Берман 1971.
22. Смит 1958, с. 295.
23. Минас-Нерпель 2007.
24. Кромвель 1997, с. 4.
25. "Кости подземелий и драконов" . gmdice.com . Проверено 20 августа 2019 г.
26. Фланаган и Грегори 2015, с. 85.
27. Штраус и Штраус 2008, с. 35–62.
28. Геккель 1904; Кромвель 1997, с. 6.

Рекомендации

• Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329–352. дои : 10.1016/0016-0032(71)90071-8. МР  0290245.
• Бикл, Аллан (2020). Основы теории графов. Американское математическое общество . ISBN 9781470455491.
• Боровик, Александр (2006). «Теория Кокстера: когнитивные аспекты». В Дэвисе, Чендлер; Эллерс, Эрих (ред.). Наследие Кокстера. Провиденс, Род-Айленд: Американское математическое общество. стр. 17–43. ISBN 978-0821837221.
• Букер, МЫ; Эгглтон, РБ (1969). «Платоновы тела (Решение задачи E2053)». Американский математический ежемесячник . 76 (2): 192. дои : 10.2307/2317282. JSTOR  2317282.
• Коксетер, HSM (1973). «2.1 Правильные многогранники; 2.2 Взаимопоступательное движение». Правильные многогранники (3-е изд.). Дуврские публикации. стр. 16–17. ISBN 0-486-61480-8. МР  0370327.
• Коксетер, HSM ; дю Валь, Патрик ; Флатер, ХТ; Петри, Дж. Ф. (1938). Пятьдесят девять икосаэдров . Том. 6. Исследования Университета Торонто (математическая серия).
• Кромвель, Питер Р. (1997). Многогранники. Издательство Кембриджского университета . ISBN 978-0-521-55432-9.
• Канди, Х. Мартин (1952). «Дельтаэдры». Математический вестник . 36 (318): 263–266. дои : 10.2307/3608204. JSTOR  3608204. S2CID  250435684.
• Фланаган, Киран; Грегори, Дэн (2015). Эгоистичный, напуганный и глупый: перестаньте бороться с человеческой природой и повысьте свою производительность, вовлеченность и влияние. Джон Уайли и сыновья . ISBN 9780730312796.
• Геккель, Э. (1904). Kunstformen der Natur (на немецком языке).См. здесь онлайн-книгу.
• Херрманн, Дайан Л.; Салли, Пол Дж. (2013). Число, форма и симметрия: введение в теорию чисел, геометрию и теорию групп. ЦРК Пресс. ISBN 978-1-4665-5464-1.
• Герц-Фишлер, Роджер (2013). Математическая история золотого числа. Публикации Курьера Дувра. ISBN 9780486152325.
• Хопкинс, Брайан (2004). «Гамильтоновы пути на платоновых графах». Международный журнал математики и математических наук . 2004 (30): 1613–1616. дои : 10.1155/S0161171204307118.{{cite journal}}: CS1 maint: unflagged free DOI (link)
• Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями». Канадский математический журнал . 18 : 169–200. doi : 10.4153/cjm-1966-021-8. МР  0185507. Збл  0132.14603.
• Джонс, Дэниел (2003) [1917]. Роуч, Питер; Хартманн, Джеймс; Сеттер, Джейн (ред.). Словарь английского произношения . Кембридж: Издательство Кембриджского университета. ISBN 3-12-539683-2.
• Кляйн, Феликс (1888). Лекции по икосаэдру и решению уравнений пятой степени. Курьерская корпорация. ISBN 978-0-486-49528-6, Дуврское издание{{cite book}}: CS1 maint: postscript (link), перевод с Кляйна, Феликса (1884). Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade. Тойбнер.
• Маклин, Кеннет Дж. М. (2007). Геометрический анализ платоновых тел и других полуправильных многогранников . Любящая исцеляющая пресса. ISBN 978-1-932690-99-6.
• Минас-Нерпель, Мартина (2007). «Демотический вписанный икосаэдр из оазиса Дахле». Журнал египетской археологии . 93 : 137–148. дои : 10.1177/030751330709300107. JSTOR  40345834.
• Шавинина, Лариса В. (2013). Международный справочник Routledge по инновационному образованию . Рутледж. ISBN 978-0-203-38714-6.
• Сильвестр, Джон Р. (2001). Геометрия: древняя и современная . Издательство Оксфордского университета.
• Симмонс, Джордж Ф. (2007). Gems исчисления: краткие жизни и памятная математика . Математическая ассоциация Америки. ISBN 9780883855614.
• Смит, Дэвид Э. (1958). История математики. Том. 2. Дуврские публикации. ISBN 0-486-20430-8.
• Штайнмиц, Николь Ф.; Манчестер, Марианна (2011). Вирусные наночастицы: инструменты для материаловедения и биомедицины . Пан Стэнфордское издательство. ISBN 978-981-4267-94-6.
• Штраус, Джеймс Х.; Штраус, Эллен Г. (2008). «Строение вирусов». Вирусы и болезни человека . Эльзевир. дои : 10.1016/b978-0-12-373741-0.50005-2. ISBN 9780123737410. S2CID  80803624.
• Саттон, Дауд (2002). Платоновые и архимедовы тела. Деревянные книги. Издательство Блумсбери США. ISBN 9780802713865.
• Стееб, Вилли-Ханс; Харди, Йорик; Танский, Игорь (2012). Проблемы и решения для групп, групп Ли, алгебр Ли с приложениями. Мировое научное издательство. ISBN 9789813104112.</ref>

Внешние ссылки

• Клитцинг, Ричард. «3D выпуклые однородные многогранники x3o5o – ike».
• Хартли, Майкл. «Математические игры доктора Майка для детей».
• К.Дж.М. Маклин, Геометрический анализ пяти платоновых тел и других полуправильных многогранников
• Многогранники виртуальной реальности Энциклопедия многогранников
• Tulane.edu Обсуждение вирусной структуры и икосаэдра
• Многогранники оригами – модели, сделанные с помощью модульного оригами.
• Видео икосаэдрической зеркальной скульптуры
• [1] Принцип вирусной архитектуры