Тангенциальный четырехугольник

Многоугольник, все четыре стороны которого касаются окружности

Описанный четырехугольник с вписанной окружностью

В евклидовой геометрии касательный четырёхугольник ( иногда просто касательный четырёхугольник ) или описанный четырёхугольник — это выпуклый четырёхугольник , все стороны которого могут касаться одной окружности внутри четырёхугольника. Эта окружность называется вписанной окружностью четырёхугольника или его вписанной окружностью, её центр — инцентр , а её радиус называется вписанным радиусом . Поскольку эти четырёхугольники можно нарисовать окружающими или описывающими их вписанные окружности, их также называют описанными четырёхугольниками , описанными четырёхугольниками и описанными четырёхугольниками . ^[1] Касательные четырёхугольники являются частным случаем касательных многоугольников .

Другие, менее часто используемые названия для этого класса четырёхугольников — вписываемый четырёхугольник , вписываемый четырёхугольник , вписанный четырёхугольник , вписанный четырёхугольник и со-вписанный четырёхугольник . ^{[1] [2]} Из-за риска путаницы с четырёхугольником, имеющим описанную окружность, который называется вписанным четырёхугольником или вписанным четырёхугольником, предпочтительнее не использовать ни одно из последних пяти названий. ^[1]

Все треугольники могут иметь вписанную окружность, но не все четырехугольники могут. Примером четырехугольника, который не может быть касательным, является неквадратный прямоугольник . В характеристиках раздела ниже указано, каким необходимым и достаточным условиям должен удовлетворять четырехугольник, чтобы иметь вписанную окружность.

Особые случаи

Примерами касательных четырехугольников являются воздушные змеи , которые включают ромбы , которые в свою очередь включают квадраты . Воздушные змеи — это в точности касательные четырехугольники, которые также являются ортодиагональными . ^[3] Прямой воздушный змей — это воздушный змей с описанной окружностью . Если четырехугольник является одновременно касательным и вписанным , он называется бицентрическим четырехугольником , а если он одновременно касательный и трапеция , он называется касательной трапецией .

Характеристика

В касательном четырехугольнике четыре биссектрисы пересекаются в центре вписанной окружности. Наоборот, выпуклый четырехугольник, в котором четыре биссектрисы пересекаются в одной точке, должен быть касательным, а общая точка — инцентром. ^[4]

Согласно теореме Пито , две пары противоположных сторон в описанном четырехугольнике в сумме дают одну и ту же общую длину, которая равна полупериметру s четырехугольника :

${\displaystyle a+c=b+d={\frac {a+b+c+d}{2}}=s.}$

Наоборот, выпуклый четырехугольник, в котором a + c = b + d, должен быть касательным. ^{[1] : стр.65  [4]}

Если противоположные стороны выпуклого четырехугольника ABCD (не являющегося трапецией ) пересекаются в точках E и F , то он является касательным тогда и только тогда, когда выполняется одно из следующих условий ^[4]:

${\displaystyle \displaystyle BE+BF=DE+DF}$

или

${\displaystyle \displaystyle AE-EC=AF-FC:}$

Другим необходимым и достаточным условием является то, что выпуклый четырехугольник ABCD является касательным тогда и только тогда, когда вписанные окружности двух треугольников ABC и ADC касаются друг друга. [ ^{1] : стр.66}

Характеристика углов, образованных диагональю BD и четырьмя сторонами четырехугольника ABCD, принадлежит Иосифеску. В 1954 году он доказал, что выпуклый четырехугольник имеет вписанную окружность тогда и только тогда, когда ^[5]

${\displaystyle \tan {\frac {\angle ABD}{2}}\cdot \tan {\frac {\angle BDC}{2}}=\tan {\frac {\angle ADB}{2}}\cdot \tan {\frac {\angle DBC}{2}}.}$

Описанный четырехугольник (синего цвета) с вписанной окружностью (пунктирная линия) и четырьмя внешними касательными окружностями (красного цвета), каждая из которых касается данной стороны и продолжений смежных сторон.

Далее, выпуклый четырехугольник с последовательными сторонами a , b , c , d является касательным тогда и только тогда, когда

${\displaystyle R_{a}R_{c}=R_{b}R_{d}}$

где R _a , R _b , R _c , R _d — радиусы окружностей, внешне касающихся сторон a , b , c , d соответственно, и расширения двух смежных сторон для каждой стороны. ^{[6] : стр.72}

Известно еще несколько характеристик четырех подтреугольников, образованных диагоналями.

Точки контакта и длины касательных

Касательный четырехугольник (синий) и его контактный четырехугольник (зеленый), соединяющий четыре точки контакта между вписанной окружностью и сторонами. Также показаны хорды касания, соединяющие противоположные точки контакта (красные) и длины касательных на сторонах

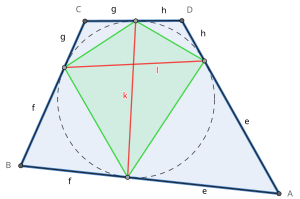
Вписанная окружность касается каждой стороны в одной точке контакта . Эти четыре точки определяют новый четырехугольник внутри исходного четырехугольника: четырехугольник контакта, который является вписанным, поскольку он вписан во вписанную окружность исходного четырехугольника.

Восемь касательных длин ( e , f , g , h на рисунке справа) касательного четырехугольника — это отрезки прямых от вершины до точек соприкосновения. Из каждой вершины выходят две конгруэнтные касательные длины.

Две хорды касания ( k и l на рисунке) касательного четырехугольника — это отрезки, соединяющие точки касания на противоположных сторонах. Они также являются диагоналями контактного четырехугольника.

Область

Нетригонометрические формулы

Площадь K описанного четырехугольника определяется по формуле

${\displaystyle \displaystyle K=r\cdot s,}$

где s — полупериметр , а r — вписанный радиус . Другая формула — ^[7]

${\displaystyle \displaystyle K={\tfrac {1}{2}}{\sqrt {p^{2}q^{2}-(ac-bd)^{2}}}}$

что дает площадь через диагонали p , q и стороны a , b , c , d описанного четырехугольника.

Площадь также может быть выражена через четыре длины касательных. Если это e , f , g , h , то касательный четырехугольник имеет площадь ^[3]

${\displaystyle \displaystyle K={\sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}}.}$

Кроме того, площадь описанного четырехугольника может быть выражена через стороны a, b, c, d и последовательные длины касательных e, f, g, h следующим образом ^{[3] : стр.128}

${\displaystyle K={\sqrt {abcd-(eg-fh)^{2}}}.}$

Поскольку eg = fh тогда и только тогда, когда описанный четырехугольник также является вписанным и, следовательно, бицентрическим, ^[8] это показывает, что максимальная площадь имеет место тогда и только тогда, когда описанный четырехугольник является бицентрическим. ${\displaystyle {\sqrt {abcd}}}$

Тригонометрические формулы

Тригонометрическая формула для площади через стороны a , b , c , d и два противолежащих угла: ^{[7] [9] [10] [11} ]

${\displaystyle \displaystyle K={\sqrt {abcd}}\sin {\frac {A+C}{2}}={\sqrt {abcd}}\sin {\frac {B+D}{2}}.}$

Для заданных длин сторон площадь максимальна , когда четырехугольник также является вписанным и, следовательно, бицентрическим четырехугольником . Тогда, поскольку противолежащие углы являются дополнительными углами . Это можно доказать другим способом, используя исчисление . ^[12] ${\displaystyle K={\sqrt {abcd}}}$

Другая формула для площади описанного четырехугольника ABCD , которая включает два противолежащих угла, выглядит следующим образом ^{[10] : стр.19}

${\displaystyle K=\left(IA\cdot IC+IB\cdot ID\right)\sin {\frac {A+C}{2}}}$

где I — инцентр.

Фактически, площадь можно выразить через две смежные стороны и два противолежащих угла как ^[7]

${\displaystyle K=ab\sin {\frac {B}{2}}\csc {\frac {D}{2}}\sin {\frac {B+D}{2}}.}$

Еще одна формула площади — ^[7]

${\displaystyle K={\tfrac {1}{2}}|(ac-bd)\tan {\theta }|,}$

где θ — один из углов между диагоналями. Эту формулу нельзя использовать, когда касательный четырехугольник — воздушный змей, поскольку тогда θ равен 90° и функция касательной не определена.

Неравенства

Как косвенно отмечено выше, площадь описанного четырехугольника со сторонами a , b , c , d удовлетворяет условию

${\displaystyle K\leq {\sqrt {abcd}}}$

с равенством тогда и только тогда, когда это вписанно-описанный четырёхугольник .

По данным Т.А. Ивановой (1976 г.), полупериметр s описанного четырехугольника удовлетворяет уравнению

${\displaystyle s\geq 4r}$

где r — вписанный радиус. Равенство имеет место тогда и только тогда, когда четырехугольник является квадратом . [ ^13] Это означает, что для площади K = rs имеет место неравенство

${\displaystyle K\geq 4r^{2}}$

с равенством тогда и только тогда, когда описанный четырехугольник является квадратом.

Свойства раздела

Тангенциальный четырехугольник с радиусом вписанной окружности r

Четыре отрезка между центром вписанной окружности и точками, где она касается четырехугольника, делят четырехугольник на четыре прямоугольных змея .

Если линия пересекает касательный четырехугольник на два многоугольника с равными площадями и равными периметрами , то эта линия проходит через инцентр . ^[4]

Внутренний радиус

Радиус вписанной окружности в тангенциальном четырехугольнике с последовательными сторонами a , b , c , d определяется по формуле ^[7]

${\displaystyle r={\frac {K}{s}}={\frac {K}{a+c}}={\frac {K}{b+d}}}$

где K — площадь четырехугольника, а s — его полупериметр. Для описанного четырехугольника с заданными сторонами радиус вписанной окружности максимален , когда четырехугольник также является вписанным (и, следовательно, вписанно-описанным ).

В терминах длин касательных вписанная окружность имеет радиус ^{[8] : Лемма2  [14]}

${\displaystyle \displaystyle r={\sqrt {\frac {efg+fgh+ghe+hef}{e+f+g+h}}}.}$

Радиус вписанной окружности также может быть выражен через расстояния от инцентра I до вершин тангенциального четырехугольника ABCD . Если u = AI , v = BI , x = CI и y = DI , то

${\displaystyle r=2{\sqrt {\frac {(\sigma -uvx)(\sigma -vxy)(\sigma -xyu)(\sigma -yuv)}{uvxy(uv+xy)(ux+vy)(uy+vx)}}}}$

где . ^[15] ${\displaystyle \sigma ={\tfrac {1}{2}}(uvx+vxy+xyu+yuv)}$

Если вписанные окружности треугольников ABC , BCD , CDA , DAB имеют радиусы соответственно, то радиус вписанной окружности описанного четырехугольника ABCD определяется по формуле ${\displaystyle r_{1},r_{2},r_{3},r_{4}}$

${\displaystyle r={\frac {G+{\sqrt {G^{2}-4r_{1}r_{2}r_{3}r_{4}(r_{1}r_{3}+r_{2}r_{4})}}}{2(r_{1}r_{3}+r_{2}r_{4})}}}$

где . ^[16] ${\displaystyle G=r_{1}r_{2}r_{3}+r_{2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{1}r_{2}}$

Формулы угла

Если e , f , g и h — длины касательных из вершин A , B , C и D соответственно до точек, где вписанная окружность касается сторон описанного четырехугольника ABCD , то углы четырехугольника можно вычислить из ^[3]

${\displaystyle \sin {\frac {A}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(e+f)(e+g)(e+h)}}},}$

${\displaystyle \sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(f+e)(f+g)(f+h)}}},}$

${\displaystyle \sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(g+e)(g+f)(g+h)}}},}$

${\displaystyle \sin {\frac {D}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(h+e)(h+f)(h+g)}}}.}$

Угол между касательными хордами k и l определяется по формуле ^[3]

${\displaystyle \sin {\varphi }={\sqrt {\frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+h)(h+e)}}}.}$

Диагонали

Если e , f , g и h — длины касательных от точек A , B , C и D соответственно до точек, где вписанная окружность касается сторон описанного четырехугольника ABCD , то длины диагоналей p = AC и q = BD равны ^{[8] : Лемма3}

${\displaystyle \displaystyle p={\sqrt {{\frac {e+g}{f+h}}{\Big (}(e+g)(f+h)+4fh{\Big )}}},}$

${\displaystyle \displaystyle q={\sqrt {{\frac {f+h}{e+g}}{\Big (}(e+g)(f+h)+4eg{\Big )}}}.}$

Аккорды касания

Если e , f , g и h — длины касательных окружностей четырехугольника, то длины хорд касания равны ^[3]

${\displaystyle \displaystyle k={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+f)(g+h)(e+g)(f+h)}}},}$

${\displaystyle \displaystyle l={\frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+h)(f+g)(e+g)(f+h)}}}}$

где касательная хорда длины k соединяет стороны длиной a = e + f и c = g + h , а касательная хорда длины l соединяет стороны длиной b = f + g и d = h + e . Квадрат отношения касательных хорд удовлетворяет ^[3]

${\displaystyle {\frac {k^{2}}{l^{2}}}={\frac {bd}{ac}}.}$

Две касательные хорды

• перпендикулярны тогда и только тогда , когда тангенциальный четырехугольник также имеет описанную окружность (он является бицентрическим ). ^{[3] : стр.124}
• имеют одинаковую длину тогда и только тогда, когда касательный четырехугольник является воздушным змеем . ^{[17] : стр.166}

Хорда касания между сторонами AB и CD в описанном четырехугольнике ABCD длиннее, чем хорда между сторонами BC и DA тогда и только тогда, когда бимедиана между сторонами AB и CD короче, чем хорда между сторонами BC и DA . ^{[18] : стр.162}

Если касательный четырехугольник ABCD имеет точки касания W на AB и Y на CD , и если касательная хорда WY пересекает диагональ BD в точке M , то отношение длин касательных равно отношению отрезков диагонали BD . ^[19] ${\displaystyle {\tfrac {BW}{DY}}}$ ${\displaystyle {\tfrac {BM}{DM}}}$

Коллинеарные точки

_{Построение линии Ньютона (красного цвета) описанного} четырехугольника (синего цвета), показывающее совмещение инцентров I , середин диагоналей M1 и M2 и середины M3 отрезка JK (зеленого цвета) _, соединяющего пересечение противолежащих сторон.

Если M ₁ и M ₂ являются серединами диагоналей AC и BD соответственно в описанном четырехугольнике ABCD с центром вписанной окружности I , и если пары противоположных сторон пересекаются в точках J и K , а M ₃ является серединой JK , то точки M ₃ , M ₁ , I и M ₂ лежат на одной прямой . ^{[4] : стр.42} Прямая, содержащая их, является линией Ньютона четырехугольника.

Если продолжения противоположных сторон в касательном четырехугольнике пересекаются в точках J и K , а продолжения противоположных сторон в его контактном четырехугольнике пересекаются в точках L и M , то четыре точки J , L , K и M лежат на одной прямой. ^{[20] : Cor.3}

Описанный четырехугольник разбит на четыре треугольника, встречающиеся в его инцентре I , их ортоцентры (фиолетовые) и точка пересечения диагоналей P (зеленые) лежат на одной прямой.

Если вписанная окружность касается сторон AB , BC , CD , DA в точках _T1 , T2 , T3 , T4 соответственно , и если N1 , _N2 , N3 , N4 являются изотомически сопряженными точками _этих точек относительно соответствующих сторон (то есть AT1 = BN1 _{и так} далее _{) ,} то точка Нагеля касательного четырехугольника определяется как пересечение прямых N1N3 _и N2N4 . _{Обе эти} прямые _делят периметр четырехугольника на две равные части. Что еще более важно, точка Нагеля _N , _« центроид площади» G и инцентр I лежат на одной прямой в этом порядке, и _NG = 2GI . Эта линия называется линией Нагеля касательного четырехугольника. ^[21]

В описанном четырехугольнике ABCD с центром вписанной окружности I и диагоналями, пересекающимися в точке P , пусть H _X , H _Y , H _Z , H _W будут ортоцентрами треугольников AIB , BIC , CID , DIA . Тогда точки P , H _X , H _Y , H _Z , H _W лежат на одной прямой. ^{[10] : с.28}

Конкурентные и перпендикулярные линии

Две диагонали и две касательные хорды являются параллельными . ^{[11] [10] : стр.11} Один из способов увидеть это — как предельный случай теоремы Брианшона , которая гласит, что шестиугольник, все стороны которого касаются одного конического сечения , имеет три диагонали, которые пересекаются в точке. Из касательного четырехугольника можно образовать шестиугольник с двумя углами 180°, поместив две новые вершины в две противоположные точки касания; все шесть сторон этого шестиугольника лежат на прямых, касательных к вписанной окружности, так что его диагонали пересекаются в точке. Но две из этих диагоналей совпадают с диагоналями касательного четырехугольника, а третья диагональ шестиугольника является прямой, проходящей через две противоположные точки касания. Повторение этого же аргумента с двумя другими точками касания завершает доказательство результата.

Если продолжения противоположных сторон в касательном четырехугольнике пересекаются в точках J и K , а диагонали пересекаются в точке P , то JK перпендикулярна продолжению IP , где I — инцентр. ^{[20] : Cor.4}

Инцентр

Центр вписанной окружности описанного четырехугольника лежит на его линии Ньютона (которая соединяет середины диагоналей). ^{[22] : Теор. 3}

Отношение двух противоположных сторон в описанном четырехугольнике можно выразить через расстояния между центром вписанной окружности I и вершинами согласно ^{[10] : стр.15}

${\displaystyle {\frac {AB}{CD}}={\frac {IA\cdot IB}{IC\cdot ID}},\quad \quad {\frac {BC}{DA}}={\frac {IB\cdot IC}{ID\cdot IA}}.}$

Произведение двух смежных сторон в описанном четырехугольнике ABCD с центром вписанной окружности I удовлетворяет ^[23]

${\displaystyle AB\cdot BC=IB^{2}+{\frac {IA\cdot IB\cdot IC}{ID}}.}$

Если I — инцентр описанного четырехугольника ABCD , то ^{[10] : стр.16}

${\displaystyle IA\cdot IC+IB\cdot ID={\sqrt {AB\cdot BC\cdot CD\cdot DA}}.}$

Центр вписанной окружности I в описанном четырехугольнике ABCD совпадает с «центром тяжести вершины» четырехугольника тогда и только тогда, когда ^{[10] : стр.22}

${\displaystyle IA\cdot IC=IB\cdot ID.}$

Если M _p и M _q являются серединами диагоналей AC и BD соответственно в описанном четырехугольнике ABCD с центром вписанной окружности I , то ^{[10] : стр.19  [24]}

${\displaystyle {\frac {IM_{p}}{IM_{q}}}={\frac {IA\cdot IC}{IB\cdot ID}}={\frac {e+g}{f+h}}}$

где e , f , g и h — длины касательных в точках A , B , C и D соответственно. Объединяя первое равенство с предыдущим свойством, «вершинный центроид» тангенциального четырехугольника совпадает с инцентром тогда и только тогда, когда инцентр является серединой отрезка, соединяющего середины диагоналей.

Если четырехзвенная связь выполнена в форме касательного четырехугольника, то она останется касательной независимо от того, как сгибается связь, при условии, что четырехугольник остается выпуклым. ^{[25] [26]} (Так, например, если квадрат деформируется в ромб, он остается касательным, хотя и к меньшей вписанной окружности). Если одна сторона удерживается в фиксированном положении, то при сгибании четырехугольника вписанный центр описывает окружность радиуса, где a, b, c, d — стороны в последовательности, а s — полупериметр. ${\displaystyle {\sqrt {abcd}}/s}$

Характеристика в четырех подтреугольниках

Характеристика Чао и Симеонова в терминах радиусов окружностей внутри каждого из четырех треугольников

В неперекрывающихся треугольниках APB , BPC , CPD , DPA, образованных диагоналями выпуклого четырехугольника ABCD , где диагонали пересекаются в точке P , имеются следующие характеристики описанных четырехугольников.

Пусть r ₁ , r ₂ , r ₃ и r ₄ обозначают радиусы вписанных окружностей в четырех треугольниках APB , BPC , CPD и DPA соответственно. Чао и Симеонов доказали, что четырехугольник является касательным тогда и только тогда, когда ^[27]

${\displaystyle {\frac {1}{r_{1}}}+{\frac {1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1}{r_{4}}}.}$

Эта характеристика была доказана пятью годами ранее Вайнштейном. ^{[17] : с.169  [28]} В решении его задачи похожая характеристика была дана Васильевым и Сендеровым. Если h ₁ , h ₂ , h ₃ и h ₄ обозначают высоты в тех же четырех треугольниках (от диагонального пересечения до сторон четырехугольника), то четырехугольник является касательным тогда и только тогда, когда ^{[5] [28]}

${\displaystyle {\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1}{h_{4}}}.}$

Другая похожая характеристика касается вневписанных радиусов r _a , r _b , r _c и r _d в тех же четырех треугольниках (четыре вневписанные окружности касаются одной стороны четырехугольника и продолжений его диагоналей). Четырехугольник является вписанным тогда и только тогда, когда ^{[1] : стр.70}

${\displaystyle {\frac {1}{r_{a}}}+{\frac {1}{r_{c}}}={\frac {1}{r_{b}}}+{\frac {1}{r_{d}}}.}$

Если R ₁ , R ₂ , R ₃ и R ₄ обозначают радиусы описанных окружностей треугольников APB , BPC , CPD и DPA соответственно, то четырехугольник ABCD является касательным тогда и только тогда, когда ^{[29] : стр. 23–24}

${\displaystyle R_{1}+R_{3}=R_{2}+R_{4}.}$

В 1996 году Вайнштейн, вероятно, был первым, кто доказал еще одну прекрасную характеристику касательных четырехугольников, которая позже появилась в нескольких журналах и на веб-сайтах. ^{[1] : стр. 72–73} В ней говорится, что когда выпуклый четырехугольник разделен на четыре неперекрывающихся треугольника его двумя диагоналями, то вписанные центры четырех треугольников являются конциклическими тогда и только тогда, когда четырехугольник является касательным. Фактически, вписанные центры образуют ортодиагональный вписанный четырехугольник . ^{[1] : стр. 74} Связанный результат заключается в том, что вписанные окружности можно заменить на вневписанные окружности тех же треугольников (касательные к сторонам четырехугольника и продолжениям его диагоналей). Таким образом, выпуклый четырехугольник является касательным тогда и только тогда, когда центры вневписанных окружностей в этих четырех вневписанных окружностях являются вершинами вписанного четырехугольника . ^{[1] : стр. 73}

Выпуклый четырехугольник ABCD с диагоналями, пересекающимися в точке P , является касательным тогда и только тогда _, когда четыре центра вневписанных окружностей в треугольниках APB , BPC , CPD и DPA _, лежащие напротив вершин B и D, являются концентрическими. ^{[1] : стр. 79} Если Ra , Rb , Rc и Rd являются радиусами вневписанных окружностей в треугольниках _APB , BPC , CPD и DPA соответственно напротив вершин B и D , то еще одно условие состоит в том, что четырехугольник является касательным тогда и только тогда, когда _[ ^{1] : стр. 80}

${\displaystyle {\frac {1}{R_{a}}}+{\frac {1}{R_{c}}}={\frac {1}{R_{b}}}+{\frac {1}{R_{d}}}.}$

Далее, выпуклый четырехугольник ABCD с диагоналями, пересекающимися в точке P, является касательным тогда и только тогда, когда ^[5]

${\displaystyle {\frac {a}{\triangle (APB)}}+{\frac {c}{\triangle (CPD)}}={\frac {b}{\triangle (BPC)}}+{\frac {d}{\triangle (DPA)}}}$

где ∆( APB ) — площадь треугольника APB .

Обозначим отрезки, на которые диагональное пересечение P делит диагональ AC , как AP = p ₁ и PC = p ₂ , и аналогично P делит диагональ BD на отрезки BP = q ₁ и PD = q ₂ . Тогда четырехугольник является касательным тогда и только тогда, когда верно одно из следующих равенств: ^[30]

${\displaystyle ap_{2}q_{2}+cp_{1}q_{1}=bp_{1}q_{2}+dp_{2}q_{1}}$

или ^{[1] : стр. 74}

${\displaystyle {\frac {(p_{1}+q_{1}-a)(p_{2}+q_{2}-c)}{(p_{1}+q_{1}+a)(p_{2}+q_{2}+c)}}={\frac {(p_{2}+q_{1}-b)(p_{1}+q_{2}-d)}{(p_{2}+q_{1}+b)(p_{1}+q_{2}+d)}}}$

или ^{[1] : стр. 77}

${\displaystyle {\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c-p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_{2}+q_{1})(d-p_{1}+q_{2})}}.}$

Условия, при которых тангенциальный четырехугольник является другим типом четырехугольника

Ромб

Описанный четырехугольник является ромбом тогда и только тогда, когда его противолежащие углы равны. ^[31]

Летающий змей

Описанный четырехугольник является воздушным змеем тогда и только тогда, когда выполняется хотя бы одно из следующих условий: ^[17]

• Площадь равна половине произведения диагоналей .
• Диагонали перпендикулярны .
• Два отрезка, соединяющие противоположные точки касания, имеют одинаковую длину.
• Одна пара противоположных касательных имеет равные длины.
• Бимедианные линии имеют одинаковую длину.
• Произведения противоположных сторон равны.
• Центр вписанной окружности лежит на диагонали, которая является осью симметрии.

Бицентрический четырехугольник

Вписанно-описанная окружность четырехугольника ABCD : контактный четырехугольник (розовый) является ортодиагональным.

Если вписанная окружность касается сторон AB , BC , CD , DA в точках W , X , Y , Z соответственно, то описанный четырехугольник ABCD также является вписанным (и, следовательно, бицентрическим ) тогда и только тогда, когда выполняется любое из следующих условий: ^{[2] [3] : стр.124  [20]}

• WY перпендикулярна XZ
• ${\displaystyle AW\cdot CY=BW\cdot DY}$
• ${\displaystyle {\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}}$

Первое из этих трех означает, что контактный четырехугольник WXYZ является ортодиагональным четырехугольником .

Описанный четырехугольник является бицентрическим тогда и только тогда, когда его радиус вписанной окружности больше, чем у любого другого описанного четырехугольника, имеющего ту же последовательность длин сторон. ^{[32] : стр.392–393}

Тангенциальная трапеция

Если вписанная окружность касается сторон AB и CD в точках W и Y соответственно, то описанный четырехугольник ABCD также является трапецией с параллельными сторонами AB и CD тогда и только тогда, когда ^{[33] : Теор. 2}

${\displaystyle AW\cdot DY=BW\cdot CY}$

и AD и BC являются параллельными сторонами трапеции тогда и только тогда, когда

${\displaystyle AW\cdot BW=CY\cdot DY.}$

Смотрите также

• Описанная окружность
• Экс-тангенциальный четырехугольник
• Тангенциальный треугольник
• Касательный многоугольник

Ссылки

1. Йозефссон, Мартин (2011), «Больше характеристик касательных четырехугольников» (PDF) , Forum Geometricorum , 11 : 65–82.
2. Брайант, Виктор; Дункан, Джон (2010), «Колеса внутри колес», The Mathematical Gazette , 94 (ноябрь): 502–505.
3. Йозефссон, Мартин (2010), «Вычисления, касающиеся длин касательных и хорд касательных касательного четырехугольника» (PDF) , Forum Geometricorum , 10 : 119–130.
4. Андрееску, Титу; Энеску, Богдан (2006), Сокровища математической олимпиады , Биркхойзер, стр. 64–68..
5. Minculete, Nicusor (2009), «Характеристики тангенциального четырехугольника» (PDF) , Forum Geometricorum , 9 : 113–118.
6. Йозефссон, Мартин (2012), «Подобные метрические характеристики касательных и экстангенциальных четырехугольников» (PDF) , Forum Geometricorum , 12 : 63–77
7. Дарелл, CV; Робсон, A. (2003), Продвинутая тригонометрия , переиздание Dover, стр. 28–30.
8. Hajja, Mowaffaq (2008), «Условие того, что описанный четырехугольник является вписанным» (PDF) , Forum Geometricorum , 8 : 103–106.
9. Сиддонс, AW; Хьюз, RT (1929), Тригонометрия , Cambridge Univ. Press, стр. 203.
10. Гринберг, Дарий, Повторное рассмотрение описанных четырехугольников, 2008
11. Yiu, Paul, Евклидова геометрия , [1], 1998, стр. 156–157.
12. Хойт, Джон П. (1986), «Максимизация площади трапеции», American Mathematical Monthly , 93 (1): 54–56, doi :10.2307/2322549.
13. Пост в Art of Problem Solving, 2012
14. Хойт, Джон П. (1984), «Quickies, Q694», Mathematics Magazine , 57 (4): 239, 242.
15. Йозефссон, Мартин (2010), «О радиусе вписанной окружности касательного четырехугольника» (PDF) , Forum Geometricorum , 10 : 27–34.
16. Богомольный, Александр (2016), Отношение вписанных радиусов в вписываемом четырехугольнике, Cut-the-knot , [2].
17. Josefsson, Martin (2011), «Когда тангенциальный четырехугольник является воздушным змеем?» (PDF) , Forum Geometricorum , 11 : 165–174.
18. Йозефссон, Мартин (2011), «Площадь бицентрического четырехугольника» (PDF) , Forum Geometricorum , 11 : 155–164.
19. Гутьеррес, Антонио, «Описанный четырехугольник, диагональ, хорда, пропорция», [3], доступ 09.04.2012.
20. Йозефссон, Мартин (2010), «Характеристики бицентрических четырехугольников» (PDF) , Forum Geometricorum , 10 : 165–173.
21. Мякишев, Алексей (2006), «О двух замечательных прямых, связанных с четырехугольником» (PDF) , Forum Geometricorum , 6 : 289–295.
22. Дергиадес, Николаос; Христодулу, Димитрис М. (2017), «Два инцентра произвольного выпуклого четырехугольника» (PDF) , Forum Geometricorum , 17 : 245–254.
23. Андреску, Титу; Фэн, Зумин (2005), 103 задачи по тригонометрии из подготовки команды США IMO , Биркхойзер, стр. 176–177.
24. "Определите отношение OM/ON", пост на Art of Problem Solving, 2011
25. Бартон, Хелен (1926), «О круге, прикрепленном к разборному четырехстержневому брусу», American Mathematical Monthly , 33 (9): 462–465, doi :10.2307/2299611, JSTOR  2299611.
26. Богомольный, Александр, «Когда четырехугольник можно описать?», Интерактивный математический сборник и головоломки , [4].
27. Чао, У Вэй; Симеонов, Пламен (2000), «Когда в четырехугольники вписаны окружности (решение задачи 10698)», American Mathematical Monthly , 107 (7): 657–658, doi :10.2307/2589133.
28. Вайнштейн, И.; Васильев Н.; Сендеров В. (1995), "(Решение задачи) М1495", Квант (6): 27–28.
29. Йозефссон, Мартин (2012), «Характеристики ортодиагональных четырехугольников» (PDF) , Forum Geometricorum , 12 : 13–25.
30. Хоэн, Ларри (2011), «Новая формула, касающаяся диагоналей и сторон четырехугольника» (PDF) , Forum Geometricorum , 11 : 211–212.
31. Де Вильерс, Майкл (2011), «Равноугольные вписанные и равносторонние описанные многоугольники», Mathematical Gazette , 95 (март): 102–107.
32. Гесс, Альбрехт (2014), «Об окружности, содержащей инцентры касательных четырехугольников» (PDF) , Forum Geometricorum , 14 : 389–396.
33. Йозефссон, Мартин (2014), «Повторный взгляд на диагональный треугольник» (PDF) , Forum Geometricorum , 14 : 381–385.

Внешние ссылки

• Вайсштейн, Эрик В. , «Тангенциальный четырехугольник», MathWorld