В астрофизике горизонт событий — это граница, за которой события не могут повлиять на наблюдателя. Термин был введен Вольфгангом Риндлером в 1950-х годах. [1]
В 1784 году Джон Мичелл предположил, что гравитация может быть достаточно сильной вблизи массивных компактных объектов, которые даже свет не может покинуть. [2] В то время доминировали ньютоновская теория гравитации и так называемая корпускулярная теория света . В этих теориях, если скорость выхода гравитационного воздействия массивного объекта превышает скорость света , то свет, возникающий внутри или из него, может временно покинуть его, но вернется. В 1958 году Дэвид Финкельштейн использовал общую теорию относительности , чтобы ввести более строгое определение локального горизонта событий черной дыры как границы, за которой события любого рода не могут повлиять на внешнего наблюдателя, что привело к парадоксам информации и брандмауэра , поощряя переосмысление концепции локальных горизонтов событий и понятия черных дыр. Впоследствии было разработано несколько теорий, некоторые с горизонтами событий, а некоторые без них. Один из ведущих разработчиков теорий, описывающих черные дыры, Стивен Хокинг , предложил использовать кажущийся горизонт вместо горизонта событий, заявив: «Гравитационный коллапс создает кажущиеся горизонты, но не горизонты событий». В конце концов он пришел к выводу, что «отсутствие горизонтов событий означает, что черных дыр не существует — в смысле режимов, из которых свет не может уйти в бесконечность ». [3] [4]
Любой объект, приближающийся к горизонту со стороны наблюдателя, кажется замедляющимся, никогда не пересекая горизонт. [5] Из-за гравитационного красного смещения его изображение краснеет со временем по мере того, как объект приближается к горизонту. [6]
В расширяющейся Вселенной скорость расширения достигает — и даже превышает — скорости света, не давая сигналам перемещаться в некоторые регионы. Космический горизонт событий — это реальный горизонт событий, поскольку он влияет на все виды сигналов, включая гравитационные волны , которые распространяются со скоростью света.
Более конкретные типы горизонтов включают связанные, но различные абсолютные и кажущиеся горизонты, обнаруженные вокруг черной дыры. Другие различные типы включают:

В космологии горизонт событий наблюдаемой Вселенной — это наибольшее сопутствующее расстояние , с которого свет, испускаемый сейчас, может достичь наблюдателя в будущем. Это отличается от концепции горизонта частиц , которая представляет собой наибольшее сопутствующее расстояние, с которого свет, испускаемый в прошлом, может достичь наблюдателя в данный момент времени. Для событий, которые происходят за пределами этого расстояния, свет не имел достаточно времени, чтобы достичь нашего местоположения, даже если он был испущен в то время, когда Вселенная началась. Эволюция горизонта частиц со временем зависит от характера расширения Вселенной . Если расширение имеет определенные характеристики, части Вселенной никогда не будут наблюдаемыми, независимо от того, как долго наблюдатель ждет, пока свет из этих областей достигнет. Граница, за которой события никогда не могут быть обнаружены, — это горизонт событий, и он представляет собой максимальную протяженность горизонта частиц.
Критерий определения того, существует ли горизонт частиц для Вселенной, следующий. Определим сопутствующее расстояние d p как
В этом уравнении a — масштабный коэффициент , c — скорость света , а t 0 — возраст Вселенной. Если d p → ∞ (т. е. точки произвольно настолько далеки, насколько это возможно наблюдать), то горизонт событий не существует. Если d p ≠ ∞ , то горизонт присутствует.
Примерами космологических моделей без горизонта событий являются вселенные, в которых доминирует материя или излучение . Примером космологической модели с горизонтом событий является вселенная, в которой доминирует космологическая постоянная ( вселенная де Ситтера ).
Расчет скоростей космологических событий и горизонтов частиц был дан в статье по космологической модели FLRW , которая аппроксимирует Вселенную как состоящую из невзаимодействующих компонентов, каждый из которых является идеальной жидкостью . [7] [8]
Если частица движется с постоянной скоростью в нерасширяющейся Вселенной, свободной от гравитационных полей, любое событие, которое происходит в этой Вселенной, в конечном итоге будет наблюдаться частицей, потому что передние световые конусы от этих событий пересекают мировую линию частицы . С другой стороны, если частица ускоряется, в некоторых ситуациях световые конусы от некоторых событий никогда не пересекают мировую линию частицы. При этих условиях в (ускоряющейся) системе отсчета частицы присутствует кажущийся горизонт , представляющий границу, за которой события ненаблюдаемы.
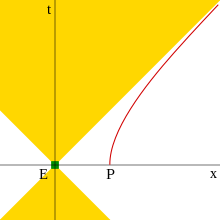
Например, это происходит с равномерно ускоренной частицей. Пространственно-временная диаграмма этой ситуации показана на рисунке справа. По мере ускорения частицы она приближается, но никогда не достигает скорости света относительно ее исходной системы отсчета. На пространственно-временной диаграмме ее путь представляет собой гиперболу , которая асимптотически приближается к 45-градусной линии (пути светового луча). Событие, край светового конуса которого является этой асимптотой или находится дальше этой асимптоты, никогда не может наблюдаться ускоряющейся частицей. В системе отсчета частицы за ней имеется граница, из-под которой не могут выйти никакие сигналы (кажущийся горизонт). Расстояние до этой границы определяется как , где a — постоянное собственное ускорение частицы.
Хотя приближения к такому типу ситуаций могут возникать в реальном мире [ требуется ссылка ] (например, в ускорителях частиц ), истинный горизонт событий никогда не присутствует, поскольку для этого требуется, чтобы частица ускорялась бесконечно (что требует произвольно большого количества энергии и произвольно большого аппарата).
В случае горизонта, воспринимаемого равномерно ускоряющимся наблюдателем в пустом пространстве, горизонт кажется остающимся на фиксированном расстоянии от наблюдателя независимо от того, как движется его окружение. Изменение ускорения наблюдателя может привести к тому, что горизонт будет казаться движущимся с течением времени или может предотвратить существование горизонта событий, в зависимости от выбранной функции ускорения. Наблюдатель никогда не касается горизонта и никогда не проходит место, где он, как кажется, находится.
В случае горизонта, воспринимаемого обитателем вселенной де Ситтера , горизонт всегда кажется находящимся на фиксированном расстоянии для неускоряющегося наблюдателя. Он никогда не соприкасается с ним, даже ускоряющимся наблюдателем.
Один из самых известных примеров горизонта событий вытекает из описания общей теорией относительности черной дыры, небесного объекта, настолько плотного, что никакая близлежащая материя или излучение не могут вырваться из ее гравитационного поля . Часто это описывается как граница, в пределах которой скорость убегания черной дыры больше скорости света . Однако более подробное описание заключается в том, что в пределах этого горизонта все светоподобные пути (пути, по которым может идти свет) (и, следовательно, все пути в передних световых конусах частиц в пределах горизонта) искривляются так, чтобы падать дальше в дыру. Как только частица оказывается внутри горизонта, движение в дыру так же неизбежно, как и движение вперед во времени — независимо от того, в каком направлении движется частица — и может рассматриваться как эквивалент этого, в зависимости от используемой системы координат пространства-времени. [10] [9] [11] [12]
Поверхность на радиусе Шварцшильда действует как горизонт событий в невращающемся теле, которое помещается внутри этого радиуса (хотя вращающаяся черная дыра действует немного иначе). Радиус Шварцшильда объекта пропорционален его массе. Теоретически, любое количество материи станет черной дырой, если сжать ее в пространство, которое помещается внутри соответствующего радиуса Шварцшильда. Для массы Солнца этот радиус составляет приблизительно 3 километра (1,9 мили); для Земли — около 9 миллиметров (0,35 дюйма). На практике, однако, ни Земля, ни Солнце не обладают необходимой массой (и, следовательно, необходимой гравитационной силой) для преодоления давления вырождения электронов и нейтронов . Минимальная масса, необходимая для коллапса звезды за пределами этих давлений, — это предел Толмена–Оппенгеймера–Волкова , который составляет приблизительно три массы Солнца.
Согласно фундаментальным моделям гравитационного коллапса, [13] горизонт событий формируется до сингулярности черной дыры. Если бы все звезды Млечного Пути постепенно стягивались к галактическому центру, сохраняя при этом пропорциональные расстояния друг от друга, они все попали бы в свой общий радиус Шварцшильда задолго до того, как их заставят столкнуться. [4] До коллапса в далеком будущем наблюдатели в галактике, окруженной горизонтом событий, продолжали бы жить обычной жизнью.
Горизонты событий черных дыр широко распространены, хотя и ошибочны. Распространенным, хотя и ошибочным, является представление о том, что черные дыры «всасывают» материал в своем окружении, тогда как на самом деле они не более способны искать материал для потребления, чем любой другой гравитационный аттрактор. Как и любая масса во Вселенной, материя должна попасть в ее гравитационную область действия, чтобы существовала возможность захвата или объединения с любой другой массой. Столь же распространенной является идея о том, что можно наблюдать падение материи в черную дыру. Это невозможно. Астрономы могут обнаружить только аккреционные диски вокруг черных дыр, где материал движется с такой скоростью, что трение создает высокоэнергетическое излучение, которое можно обнаружить (аналогично, часть материи из этих аккреционных дисков выталкивается вдоль оси вращения черной дыры, создавая видимые струи, когда эти потоки взаимодействуют с материей, такой как межзвездный газ, или когда они случайно направлены прямо на Землю). Более того, удаленный наблюдатель никогда не увидит, как что-то достигает горизонта. Вместо этого, по мере приближения к дыре, будет казаться, что объект движется все медленнее, а излучаемый им свет будет все больше и больше смещаться в красную область.
Топологически горизонт событий определяется из причинной структуры как прошлый нулевой конус будущей конформной времениподобной бесконечности. Горизонт событий черной дыры является телеологическим по своей природе, что означает, что он определяется будущими причинами. [14] [15] [16] Точнее, нужно знать всю историю Вселенной и весь путь в бесконечное будущее, чтобы определить наличие горизонта событий, что невозможно для квазилокальных наблюдателей (даже в принципе). [17] [18] Другими словами, не существует эксперимента и/или измерения, которые можно было бы выполнить в конечной области пространства-времени и в конечном временном интервале, которые бы дали ответ на вопрос, существует ли горизонт событий. Из-за чисто теоретической природы горизонта событий движущийся объект не обязательно испытывает странные эффекты и фактически проходит через вычисленную границу за конечное количество своего собственного времени . [19]
Заблуждение относительно горизонтов событий, особенно горизонтов событий черных дыр , заключается в том, что они представляют собой неизменную поверхность, которая уничтожает приближающиеся к ним объекты. На практике все горизонты событий кажутся находящимися на некотором расстоянии от любого наблюдателя, и объекты, отправленные к горизонту событий, никогда не пересекают его с точки зрения отправляющего наблюдателя (поскольку световой конус события, пересекающего горизонт, никогда не пересекает мировую линию наблюдателя ). Попытка заставить объект вблизи горизонта оставаться неподвижным относительно наблюдателя требует приложения силы, величина которой неограниченно возрастает (становясь бесконечной) по мере его приближения.
В случае горизонта вокруг черной дыры все наблюдатели, неподвижные относительно удаленного объекта, согласятся, где находится горизонт. Хотя это, кажется, позволяет наблюдателю, опущенному к отверстию на веревке (или стержне), соприкоснуться с горизонтом, на практике это невозможно. Правильное расстояние до горизонта конечно, [20] поэтому длина необходимой веревки также будет конечной, но если веревку опускать медленно (так, чтобы каждая точка на веревке находилась приблизительно в состоянии покоя в координатах Шварцшильда ), правильное ускорение ( сила тяжести ), испытываемое точками на веревке все ближе и ближе к горизонту, будет стремиться к бесконечности, поэтому веревка разорвется. Если веревку опускать быстро (возможно, даже в свободном падении ), то действительно наблюдатель внизу веревки может коснуться и даже пересечь горизонт событий. Но как только это произойдет, невозможно вытащить нижнюю часть веревки обратно из горизонта событий, поскольку, если веревку натянуть, силы вдоль веревки неограниченно возрастают по мере приближения к горизонту событий, и в какой-то момент веревка должна порваться. При этом разрыв должен произойти не на горизонте событий, а в точке, где его может наблюдать второй наблюдатель.
Предполагая, что возможный видимый горизонт находится далеко внутри горизонта событий или его нет, наблюдатели, пересекающие горизонт событий черной дыры, на самом деле не увидят и не почувствуют, что в этот момент происходит что-то особенное. С точки зрения визуального восприятия, наблюдатели, которые попадают в дыру, воспринимают возможный видимый горизонт как черную непроницаемую область, окружающую сингулярность. [21] Другие объекты, которые вошли в область горизонта по тому же радиальному пути, но в более раннее время, будут казаться ниже наблюдателя до тех пор, пока они не войдут внутрь видимого горизонта, и они смогут обмениваться сообщениями. Увеличение приливных сил также является локально заметным эффектом, как функция массы черной дыры. В реалистичных звездных черных дырах спагеттификация происходит рано: приливные силы разрывают материалы задолго до горизонта событий. Однако в сверхмассивных черных дырах , которые находятся в центрах галактик, спагеттификация происходит внутри горизонта событий. Человек-астронавт выживет при падении через горизонт событий только в черной дыре с массой приблизительно в 10 000 масс Солнца или больше. [22]
Космический горизонт событий обычно принимается как реальный горизонт событий, тогда как описание локального горизонта событий черной дыры, данное общей теорией относительности, оказывается неполным и противоречивым. [3] [4] Когда условия, при которых возникают локальные горизонты событий, моделируются с использованием более полной картины того, как работает Вселенная, которая включает как теорию относительности, так и квантовую механику , ожидается, что локальные горизонты событий будут иметь свойства, отличающиеся от тех, которые предсказываются с использованием только общей теории относительности.
В настоящее время ожидается, что механизм излучения Хокинга , что основное воздействие квантовых эффектов заключается в том, что горизонты событий обладают температурой и, таким образом, испускают излучение. Для черных дыр это проявляется как излучение Хокинга , а более широкий вопрос о том, как черная дыра обладает температурой, является частью темы термодинамики черных дыр . Для ускоряющихся частиц это проявляется как эффект Унру , который заставляет пространство вокруг частицы казаться заполненным материей и излучением.
Согласно спорной гипотезе о существовании защитной стены черной дыры , вещество, падающее в черную дыру, будет сожжено дотла высокоэнергетической «защитной стеной» на горизонте событий.
Альтернативой является принцип дополнительности , согласно которому в карте дальнего наблюдателя падающая материя термализуется на горизонте и переизлучается как излучение Хокинга, в то время как в карте падающего наблюдателя материя продолжает нетронутой проходить через внутреннюю область и разрушается в сингулярности. Эта гипотеза не нарушает теорему о неклонировании, поскольку существует единственная копия информации согласно любому данному наблюдателю. Комплементарность черных дыр фактически предполагается законами масштабирования струн, приближающихся к горизонту событий, предполагая, что в карте Шварцшильда они растягиваются, чтобы покрыть горизонт и термализуются в мембрану толщиной с длину Планка .
Полное описание локальных горизонтов событий, создаваемых гравитацией, как ожидается, как минимум потребует теории квантовой гравитации . Одной из таких теорий-кандидатов является М-теория . Другой такой теорией-кандидатом является петлевая квантовая гравитация .