Масштаб (карта)

Отношение расстояния на карте к соответствующему расстоянию на местности

Графическая или линейчатая шкала. На карте также обычно указывается ее масштаб в цифрах («1:50 000», например, означает, что один см на карте представляет 50 000 см реального пространства, что составляет 500 метров).

Линейчатая шкала с номинальным масштабом, выраженным как «1:600 ​​000», то есть 1 см на карте соответствует 600 000  см = 6  км на земле. ^[а]

Масштаб карты – это отношение расстояния на карте к соответствующему расстоянию на местности . Эта простая концепция усложняется кривизной поверхности Земли , из-за которой масштаб карты меняется. Из-за этого различия концепция масштаба приобретает смысл в двух разных смыслах.

Первый способ – это соотношение размеров образующего шара к размерам Земли. Генерирующий глобус — это концептуальная модель, до которой сжимается Земля и на основе которой проецируется карта . Отношение размера Земли к размеру образующего земного шара называется номинальным масштабом (также называемым главным масштабом или репрезентативной дробью ). На многих картах указан номинальный масштаб и может даже отображаться линейчатая шкала (иногда называемая просто «масштабом») для его обозначения.

Вторая отдельная концепция масштаба применима к изменению масштаба карты. Это отношение масштаба отображаемой точки к номинальному масштабу. В данном случае «масштаб» означает масштабный коэффициент (также называемый точечной шкалой или конкретной шкалой ).

Если область карты достаточно мала, чтобы игнорировать кривизну Земли, например, в плане города, то в качестве масштаба можно использовать одно значение, не вызывая ошибок измерений. На картах, охватывающих большие территории или всю Землю, масштаб карты может быть менее полезным или даже бесполезным для измерения расстояний. Картографическая проекция играет решающую роль в понимании того, как масштаб меняется на карте. ^{[1] [2]} Когда масштаб заметно меняется, это можно учитывать как масштабный коэффициент. Индикатриса Тиссо часто используется для иллюстрации изменения точечного масштаба на карте.

История

Основы количественного масштабирования карт восходят к древнему Китаю с текстовыми свидетельствами того, что идея масштабирования карт была понята во втором веке до нашей эры. Древние китайские геодезисты и картографы располагали обширными техническими ресурсами, используемыми для создания карт, таких как счетные стержни , плотничьи угольники , отвесы , компасы для рисования окружностей и визирные трубки для измерения наклона. На системы отсчета, постулирующие зарождающуюся систему координат для определения мест, намекали древние китайские астрономы, разделившие небо на различные сектора или лунные ложи. ^[3]

Китайский картограф и географ Пэй Сю периода Троецарствия создал набор карт большой площади, нарисованных в масштабе. Он разработал набор принципов, в которых подчеркивалась важность последовательного масштабирования, измерений направления и корректировки измерений площади местности, которая была нанесена на карту. ^[3]

Терминология

Представление масштаба

Масштабы карты могут быть выражены словами (лексический масштаб), соотношением или дробью. Примеры:

«от одного сантиметра до ста метров» или 1:10 000 или 1/10 000

«один дюйм на одну милю» или 1:63 360 или 1/63 360

«от одного сантиметра до тысячи километров» или 1:100 000 000 или 1/100 000 000. (Обычно соотношение сокращается до 1:100M)

Линейчатая шкала и лексическая шкала

В дополнение к вышесказанному многие карты имеют одну или несколько (графических) линейчатых шкал . Например, некоторые современные британские карты имеют три шкалы: по одной для километров, миль и морских миль.

Лексический масштаб на языке, известном пользователю, может быть легче визуализировать, чем пропорцию: если масштаб составляет от дюйма до двух миль и пользователь карты может видеть на карте две деревни, находящиеся на расстоянии примерно двух дюймов друг от друга, то это легко сделать. чтобы выяснить, что деревни находятся на земле примерно в четырех милях друг от друга.

Лексическая шкала может вызвать проблемы , если она выражена на языке, который пользователь не понимает, или в устаревших или плохо определенных единицах. Например, масштаб от одного дюйма до фарлонга (1:7920) будет понятен многим пожилым людям в странах, где раньше в школах преподавали имперские единицы измерения . Но масштаб одного пуса к одной лиге может составлять около 1:144 000, в зависимости от выбора картографом множества возможных определений лиги, и лишь меньшинство современных пользователей знакомо с используемыми единицами измерения.

Крупномасштабный, средний масштаб, мелкий масштаб

Контраст пространственного масштаба .

Мелкомасштабная карта охватывает большие регионы, такие как карты мира , континенты или крупные страны. Другими словами, они показывают большие площади земли на небольшом пространстве. Их называют мелкомасштабными, поскольку репрезентативная фракция относительно невелика.

На крупномасштабных картах более подробно показаны меньшие территории, например, на картах округов или планах городов. Такие карты называются крупномасштабными, поскольку репрезентативная фракция относительно велика. Например, план города, представляющий собой крупномасштабную карту, может иметь масштаб 1:10 000, тогда как карта мира, представляющая собой карту мелкого масштаба, может иметь масштаб 1:100 000 000.

В следующей таблице описаны типичные диапазоны этих шкал, но ее не следует считать авторитетной, поскольку не существует стандарта:

Термины иногда используются в абсолютном смысле таблицы, а иногда - в относительном. Например, картограф, чья работа связана исключительно с крупномасштабными картами (как указано в таблице выше), может называть карту масштаба 1:500 000 мелкомасштабной.

В английском языке слово крупномасштабный часто используется в значении «обширный». Однако, как объяснялось выше, картографы используют термин «крупномасштабный» для обозначения менее обширных карт – тех, на которых показана меньшая территория. Карты, показывающие обширную территорию, являются картами «мелкого масштаба». Это может стать причиной путаницы.

Вариант масштаба

Картографирование больших территорий вызывает заметные искажения, поскольку существенно выравнивает искривленную поверхность Земли. То, как распределяются искажения, зависит от картографической проекции . Масштаб карты варьируется , и указанный масштаб карты является лишь приблизительным. Подробно это обсуждается ниже.

Крупномасштабные карты с пренебрежением кривизной

Область, в которой Землю можно считать плоской, зависит от точности геодезических измерений . Если измерять только с точностью до метра, то кривизну Земли невозможно обнаружить на меридиональном расстоянии около 100 километров (62 мили) и на линии восток-запад около 80 км (на широте 45 градусов). При съемке с точностью до 1 миллиметра (0,039 дюйма) кривизна не обнаруживается на меридиональном расстоянии около 10 км и на линии восток-запад около 8 км. ^[4] Таким образом, план Нью-Йорка с точностью до одного метра или план строительной площадки с точностью до одного миллиметра удовлетворяют вышеуказанным условиям пренебрежения кривизной. Их можно обрабатывать с помощью плоской съемки и картировать с помощью масштабных чертежей, на которых любые две точки, находящиеся на одном и том же расстоянии на чертеже, находятся на одинаковом расстоянии на земле. Истинные наземные расстояния рассчитываются путем измерения расстояния на карте и последующего умножения на обратную дробь масштаба или, что то же самое, простого использования разделителей для переноса расстояния между точками на карте в линейчатый масштаб на карте.

Точечная шкала (или конкретная шкала)

Как доказано Теоремой Гаусса Egregium , сферу (или эллипсоид) нельзя спроецировать на плоскость без искажения. Обычно это иллюстрируют невозможностью разгладить апельсиновую корку на плоской поверхности, не порвав и не деформировав ее. Единственное истинное представление сферы в постоянном масштабе — это другая сфера, например глобус .

Учитывая ограниченный практический размер глобусов, мы должны использовать карты для детального картографирования. Карты требуют проекций. Проекция подразумевает искажение: постоянное разделение на карте не соответствует постоянному разделению на земле. Хотя на карте может отображаться графический линейчатый масштаб, этот масштаб необходимо использовать с пониманием того, что он будет точным только на некоторых линиях карты. (Это обсуждается далее в примерах в следующих разделах.)

Пусть P — точка широты и долготы на сфере (или эллипсоиде ). Пусть Q — соседняя точка, а — угол между элементом PQ и меридианом в точке P: этот угол является азимутальным углом элемента PQ. Пусть P' и Q' — соответствующие точки проекции. Угол между направлением P'Q' и проекцией меридиана является пеленгом . В общем . Комментарий: это точное различие между азимутом (на поверхности Земли) и пеленгом (на карте) не наблюдается повсеместно, многие авторы используют эти термины почти как синонимы. ${\displaystyle \varphi }$ ${\displaystyle \lambda }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \alpha \neq \beta }$

Определение: масштаб точек в точке P представляет собой отношение двух расстояний P'Q' и PQ в пределе, когда Q приближается к P. Мы запишем это как

${\displaystyle \mu (\lambda ,\,\varphi ,\,\alpha )=\lim _{Q\to P}{\frac {P'Q'}{PQ}},}$

где обозначение указывает, что точечная шкала является функцией положения P, а также направления элемента PQ.

Определение: если P и Q лежат на одном меридиане , то масштаб меридиана обозначается . ${\displaystyle (\alpha =0)}$ ${\displaystyle h(\lambda ,\,\varphi )}$

Определение: если P и Q лежат на одной параллели , параллельный масштаб обозначается . ${\displaystyle (\alpha =\pi /2)}$ ${\displaystyle k(\lambda ,\,\varphi )}$

Определение: если масштаб точки зависит только от положения, а не от направления, мы говорим, что она изотропна , и условно обозначаем ее значение в любом направлении параллельным масштабным коэффициентом . ${\displaystyle k(\lambda ,\varphi )}$

Определение: Картографическая проекция называется конформной , если угол между парой линий, пересекающихся в точке P, равен углу между проецируемыми линиями в проецируемой точке P' для всех пар линий, пересекающихся в точке P. Конформная карта имеет изотропный масштабный коэффициент. И наоборот, изотропные масштабные коэффициенты по карте подразумевают конформную проекцию.

Изотропия масштаба подразумевает, что мелкие элементы растягиваются одинаково во все стороны, то есть форма маленького элемента сохраняется. Это свойство ортоморфизма (от греческого «правильная форма»). Квалификация «маленький» означает, что при некоторой заданной точности измерения не может быть обнаружено никаких изменений масштабного коэффициента элемента. Поскольку конформные проекции имеют изотропный масштабный коэффициент, их также называют ортоморфными проекциями . Например, проекция Меркатора является конформной, поскольку она построена с учетом сохранения углов, а ее масштабный коэффициент изотропен и зависит только от широты: Меркатор действительно сохраняет форму в небольших областях.

Определение: в конформной проекции с изотропным масштабом точки, имеющие одинаковое значение масштаба, могут быть соединены, образуя линии изошкалы . Они не наносятся на карты для конечных пользователей, но присутствуют во многих стандартных текстах. (См. Снайдер ^[1], стр. 203–206.)

Репрезентативная фракция (RF) или основная шкала

При составлении уравнений любой проекции используются два соглашения. Например, равноугольную цилиндрическую проекцию можно записать как

картографы:        ${\displaystyle x=a\lambda }$       ${\displaystyle y=a\varphi }$

математики:       ${\displaystyle x=\lambda }$       ${\displaystyle y=\varphi }$

Здесь мы примем первое из этих соглашений (вслед за использованием в обзорах Снайдера). Очевидно, что приведенные выше уравнения проекции определяют положение огромного цилиндра, обернутого вокруг Земли, а затем развернутого. Мы говорим, что эти координаты определяют карту проекции , которую необходимо логически отличать от реальных напечатанных (или просмотренных) карт. Если определение точечного масштаба в предыдущем разделе дано в терминах карты проекции, то мы можем ожидать, что масштабные коэффициенты будут близки к единице. Для нормальных касательных цилиндрических проекций масштаб вдоль экватора равен k = 1, и, как правило, масштаб изменяется по мере удаления от экватора. Анализ масштаба на карте проекции — это исследование изменения k от его истинного значения, равного единице.

Настоящие печатные карты создаются на основе карты проекции с использованием постоянного масштаба, обозначаемого соотношением, например 1:100M (для карт всего мира) или 1:10000 (например, для планов городов). Чтобы избежать путаницы при использовании слова «масштаб», эта постоянная доля масштаба называется репрезентативной фракцией (RF) напечатанной карты, и ее следует идентифицировать с соотношением, напечатанным на карте. Фактические координаты напечатанной карты для равнопрямоугольной цилиндрической проекции:

распечатанная карта:        ${\displaystyle x=(RF)a\lambda }$       ${\displaystyle y=(RF)a\varphi }$

Это соглашение позволяет четко различать внутреннее масштабирование проекции и масштабирование уменьшения.

С этого момента мы игнорируем РФ и работаем с картой проекции.

Визуализация точечной шкалы: индикатриса Тиссо.

Трипельная проекция Винкеля с индикатрисой деформации Тиссо.

Рассмотрим небольшой круг на поверхности Земли с центром в точке P по широте и долготе . Поскольку масштаб точки меняется в зависимости от положения и направления, проекция круга на проекцию будет искажена. Тиссо доказал, что, пока искажение не слишком велико, на проекции круг станет эллипсом. В общем, размер, форма и ориентация эллипса будут меняться в зависимости от проекции. Наложение этих эллипсов искажения на картографическую проекцию передает способ изменения точечного масштаба на карте. Эллипс искажения известен как индикатриса Тиссо . Показанный здесь пример представляет собой трипельную проекцию Винкеля , стандартную проекцию для карт мира, созданную Национальным географическим обществом . Минимальное искажение приходится на центральный меридиан на широте 30 градусов (север и юг). (Другие примеры ^{[5] [6]} ). ${\displaystyle \varphi }$ ${\displaystyle \lambda }$

Точечная шкала для нормальных цилиндрических проекций сферы

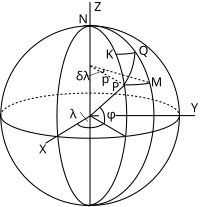
Ключом к количественному пониманию масштаба является рассмотрение бесконечно малого элемента на сфере. На рисунке показаны точки P на широте и долготе сферы. Точка Q находится на широте и долготе . Линии PK и MQ представляют собой дуги меридианов длиной где – радиус сферы и измеряется в радианах. Линии PM и KQ представляют собой дуги параллельных окружностей длиной с в радианах. При выводе точечного свойства проекции в точку P достаточно взять бесконечно малый элемент поверхности PMQK: в пределе Q, приближающегося к P, такой элемент стремится к бесконечно малому плоскому прямоугольнику. ${\displaystyle \varphi }$ ${\displaystyle \lambda }$ ${\displaystyle \varphi +\delta \varphi }$ ${\displaystyle \lambda +\delta \lambda }$ ${\displaystyle a\,\delta \varphi }$ ${\displaystyle a}$ ${\displaystyle \varphi }$ ${\displaystyle (a\cos \varphi )\delta \lambda }$ ${\displaystyle \lambda }$

Бесконечно малые элементы на сфере и нормальная цилиндрическая проекция.

Нормальные цилиндрические проекции сферы имеют и равны только функции широты. Следовательно, бесконечно малый элемент PMQK на сфере проецируется в бесконечно малый элемент P'M'Q'K', который представляет собой точный прямоугольник с основанием и высотой  . Сравнивая элементы на сфере и проекции, мы можем сразу вывести выражения для масштабных коэффициентов на параллелях и меридианах. (Рассмотрение масштаба в общем направлении можно найти ниже.) ${\displaystyle x=a\lambda }$ ${\displaystyle y}$ ${\displaystyle \delta x=a\,\delta \lambda }$ ${\displaystyle \delta y}$

параллельный масштабный коэффициент   ${\displaystyle \quad k\;=\;{\dfrac {\delta x}{a\cos \varphi \,\delta \lambda \,}}=\,\sec \varphi \qquad \qquad {}}$

масштабный коэффициент меридиана  ${\displaystyle \quad h\;=\;{\dfrac {\delta y}{a\,\delta \varphi \,}}={\dfrac {y'(\varphi )}{a}}}$

Обратите внимание, что параллельный масштабный коэффициент не зависит от определения, поэтому он одинаков для всех нормальных цилиндрических проекций. Полезно отметить, что ${\displaystyle k=\sec \varphi }$ ${\displaystyle y(\varphi )}$

на широте 30 градусов параллельный масштаб равен ${\displaystyle k=\sec 30^{\circ }=2/{\sqrt {3}}=1.15}$

на широте 45 градусов параллельный масштаб равен ${\displaystyle k=\sec 45^{\circ }={\sqrt {2}}=1.414}$

на широте 60 градусов параллельный масштаб равен ${\displaystyle k=\sec 60^{\circ }=2}$

на широте 80 градусов параллельный масштаб равен ${\displaystyle k=\sec 80^{\circ }=5.76}$

на широте 85 градусов параллельный масштаб равен ${\displaystyle k=\sec 85^{\circ }=11.5}$

Следующие примеры иллюстрируют три нормальные цилиндрические проекции, и в каждом случае изменение масштаба в зависимости от положения и направления иллюстрируется использованием индикатрисы Тиссо .

Три примера нормальной цилиндрической проекции

Равноугольная проекция

Эквидистантная проекция с индикатрисой деформации Тиссо.

Равноугольная проекция , ^{[1] [2] [4],} также известная как Plate Carrée (по-французски «плоский квадрат») или (несколько вводит в заблуждение) эквидистантная проекция, определяется формулой

${\displaystyle x=a\lambda ,}$   ${\displaystyle y=a\varphi ,}$

где - радиус сферы, - долгота от центрального меридиана проекции (здесь взятый за гринвичский меридиан в точке ) и - широта. Обратите внимание, что и выражены в радианах (полученные путем умножения градусной меры на коэффициент /180). Долгота находится в диапазоне , а широта — в диапазоне . ${\displaystyle a}$ ${\displaystyle \lambda }$ ${\displaystyle \lambda =0}$ ${\displaystyle \varphi }$ ${\displaystyle \lambda }$ ${\displaystyle \varphi }$ ${\displaystyle \pi }$ ${\displaystyle \lambda }$ ${\displaystyle [-\pi ,\pi ]}$ ${\displaystyle \varphi }$ ${\displaystyle [-\pi /2,\pi /2]}$

Поскольку в предыдущем разделе дано ${\displaystyle y'(\varphi )=1}$

параллельный масштаб,  ${\displaystyle \quad k\;=\;{\dfrac {\delta x}{a\cos \varphi \,\delta \lambda \,}}=\,\sec \varphi \qquad \qquad {}}$

меридианная шкала ${\displaystyle \quad h\;=\;{\dfrac {\delta y}{a\,\delta \varphi \,}}=\,1}$

Расчет масштаба точек в произвольном направлении см. в приложении.

На рисунке показана индикатриса Тиссо для этой проекции. На экваторе h=k=1 и круговые элементы неискажены в проекции. На более высоких широтах круги искажаются в эллипс, образуемый растяжением только в параллельном направлении: в меридиональном направлении искажений нет. Отношение большой оси к малой равно . Очевидно, что площадь эллипса увеличится во столько же раз. ${\displaystyle \sec \varphi }$

Полезно рассмотреть возможность использования линейчатых шкал, которые могут появиться в печатной версии этой проекции. На экваторе масштаб верен (k = 1), так что умножение его длины на печатной карте на обратную величину RF (или основного масштаба) дает фактическую длину окружности Земли. Линейчатая шкала на карте также отображается в истинном масштабе, поэтому перенос расстояния между двумя точками на экваторе на линейчатую шкалу даст правильное расстояние между этими точками. То же самое происходит и с меридианами. На параллели, отличной от экватора, масштаб такой, что когда мы переносим расстояние от параллели на линейную шкалу, мы должны разделить расстояние на линейчатой ​​шкале на этот коэффициент, чтобы получить расстояние между точками при измерении вдоль параллели (что не является истинное расстояние по большому кругу ). На линии с азимутом, скажем, 45 градусов ( ) масштаб постоянно меняется в зависимости от широты, и перенос разделения вдоль линии на линейчатую шкалу не дает какого-либо простого способа определения расстояния, связанного с истинным расстоянием. (Но см. дополнение). Даже если бы можно было определить расстояние вдоль этой линии постоянного плоского угла, его актуальность сомнительна, поскольку такая линия в проекции соответствует сложной кривой на сфере. По этим причинам линейчатые масштабы на картах мелкого масштаба следует использовать с особой осторожностью. ${\displaystyle \sec \varphi }$ ${\displaystyle \beta =45^{\circ }}$

Проекция Меркатора

Проекция Меркатора с индикатрисой деформации Тиссо . (Искажение неограниченно увеличивается на более высоких широтах)

Проекция Меркатора отображает сферу в прямоугольник (бесконечной протяженности в -направлении ) с помощью уравнений ^{[1] [2] [4]} ${\displaystyle y}$

${\displaystyle x=a\lambda \,}$

${\displaystyle y=a\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right]}$

где a и такие же, как в предыдущем примере. Поскольку масштабные коэффициенты: ${\displaystyle \lambda \,}$ ${\displaystyle \varphi \,}$ ${\displaystyle y'(\varphi )=a\sec \varphi }$

параллельный масштаб      ${\displaystyle k\;=\;{\dfrac {\delta x}{a\cos \varphi \,\delta \lambda \,}}=\,\sec \varphi .}$

меридианная шкала    ${\displaystyle h\;=\;{\dfrac {\delta y}{a\,\delta \varphi \,}}=\,\sec \varphi .}$

В математическом приложении показано, что масштаб точки в произвольном направлении также равен , поэтому масштаб является изотропным (одинаковым во всех направлениях), его величина увеличивается с широтой как . На диаграмме Тиссо каждый бесконечно малый круглый элемент сохраняет свою форму, но с увеличением широты увеличивается все больше и больше. ${\displaystyle \sec \varphi }$ ${\displaystyle \sec \varphi }$

Равновеликая проекция Ламберта

Нормальная цилиндрическая равновеликая проекция Ламберта с индикатрисой деформации Тиссо.

Равновеликая проекция Ламберта отображает сферу в конечный прямоугольник с помощью уравнений ^{[1] [2] [4]}

${\displaystyle x=a\lambda \qquad \qquad y=a\sin \varphi }$

где a и такие же, как в предыдущем примере. Поскольку масштабные коэффициенты ${\displaystyle \lambda }$ ${\displaystyle \varphi }$ ${\displaystyle y'(\varphi )=\cos \varphi }$

параллельный масштаб       ${\displaystyle \quad k\;=\;{\dfrac {\delta x}{a\cos \varphi \,\delta \lambda \,}}=\,\sec \varphi \qquad \qquad {}}$

меридианная шкала    ${\displaystyle \quad h\;=\;{\dfrac {\delta y}{a\,\delta \varphi \,}}=\,\cos \varphi }$

Расчет масштаба точки в произвольном направлении приведен ниже.

Вертикальный и горизонтальный масштабы теперь компенсируют друг друга (hk=1), а на диаграмме Тиссо каждый бесконечно малый круговой элемент искажается в эллипс той же площади , что и неискаженные круги на экваторе.

Графики масштабных коэффициентов

На графике показано изменение масштабных коэффициентов для трех приведенных выше примеров. На верхнем графике показана функция изотропного масштаба Меркатора: масштаб параллели такой же, как масштаб меридиана. На других графиках показан масштабный коэффициент меридиана для равноугольной проекции (h=1) и для равновеликой проекции Ламберта. Эти последние две проекции имеют параллельный масштаб, идентичный масштабу графика Меркатора. Что касается Ламберта, обратите внимание, что параллельный масштаб (как Меркатор A) увеличивается с широтой, а масштаб меридиана (C) уменьшается с широтой таким образом, что hk = 1, гарантируя сохранение площади.

Изменение масштаба проекции Меркатора

Шкала точек Меркатора равна единице на экваторе, поскольку она такова, что вспомогательный цилиндр, использованный в ее конструкции, расположен по касательной к Земле на экваторе. По этой причине обычную проекцию следует называть касательной . Масштаб меняется в зависимости от широты как . Поскольку по мере приближения к полюсам карта Меркатора стремится к бесконечности, на высоких широтах она сильно искажается, и по этой причине проекция совершенно не подходит для карт мира (если только мы не обсуждаем навигацию и румбические линии ). Однако на широте около 25 градусов значение составляет около 1,1, поэтому точность Меркатора составляет не более 10% в полосе шириной 50 градусов с центром на экваторе. Более узкие полосы лучше: полоса шириной 16 градусов (с центром на экваторе) имеет точность с точностью до 1% или 1 части из 100. ${\displaystyle k=\sec \varphi }$ ${\displaystyle \sec \varphi }$ ${\displaystyle \sec \varphi }$

Стандартным критерием хороших крупномасштабных карт является то, что точность должна быть в пределах 4 частей на 10 000, или 0,04%, что соответствует . Так как достигает этого значения в градусах (см. рисунок ниже, красная линия). Таким образом, касательная проекция Меркатора имеет высокую точность в пределах полосы шириной 3,24 градуса с центром на экваторе. Это соответствует расстоянию с севера на юг около 360 км (220 миль). Внутри этой полосы Меркатор очень хорош, очень точен и сохраняет форму, поскольку он конформен (сохраняет угол). Эти наблюдения побудили к разработке поперечных проекций Меркатора, в которых меридиан рассматривается «как экватор» проекции, так что мы получаем точную карту в пределах узкого расстояния от этого меридиана. Такие карты хороши для стран, ориентированных почти с севера на юг (например, Великобритания ), и набор из 60 таких карт используется для Универсального поперечного Меркатора (UTM) . Обратите внимание, что в обеих этих проекциях (основанных на различных эллипсоидах) уравнения преобразования x и y и выражение для масштабного коэффициента являются сложными функциями как широты, так и долготы. ${\displaystyle k=1.0004}$ ${\displaystyle \sec \varphi }$ ${\displaystyle \varphi =1.62}$

Изменение масштаба вблизи экватора для касательной (красный) и секущей (зеленый) проекций Меркатора.

Секущие, или модифицированные, проекции

Сравнение касательных и секущих цилиндрических, конических и азимутальных проекций карты со стандартными параллелями, показанными красным цветом.

Основная идея секущей проекции заключается в том, что сфера проецируется на цилиндр, который пересекает сферу по двум параллелям, скажем, на север и юг. Очевидно, что масштаб теперь верен на этих широтах, тогда как параллели ниже этих широт сжимаются проекцией, и их (параллельный) масштабный коэффициент должен быть меньше единицы. В результате отклонение шкалы от единицы уменьшается в более широком диапазоне широт. ${\displaystyle \varphi _{1}}$

Например, одна из возможных секущих проекций Меркатора определяется формулой

${\displaystyle x=0.9996a\lambda \qquad \qquad y=0.9996a\ln \left(\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right).}$

Числовые множители не меняют форму проекции, но это означает, что изменяются масштабные коэффициенты:

секущая шкала Меркатора,    ${\displaystyle \quad k\;=0.9996\sec \varphi .}$

Таким образом

• масштаб по экватору — 0,9996,
• масштаб k  = 1 на широте, заданной выражениемwhere так что градусы, ${\displaystyle \varphi _{1}}$ ${\displaystyle \sec \varphi _{1}=1/0.9996=1.00004}$ ${\displaystyle \varphi _{1}=1.62}$
• k=1,0004 на широте, заданной формулой «для каких градусов». Следовательно, проекция имеет точность 0,04% на более широкую полосу 4,58 градуса (по сравнению с 3,24 градуса для касательной формы). ${\displaystyle \varphi _{2}}$ ${\displaystyle \sec \varphi _{2}=1.0004/0.9996=1.0008}$ ${\displaystyle \varphi _{2}=2.29}$ ${\displaystyle 1<k<1.0004}$

Это иллюстрируется нижней (зеленой) кривой на рисунке предыдущего раздела.

Такие узкие зоны высокой точности используются в проекциях UTM и британской OSGB, которые представляют собой секущие поперечные проекции Меркатора на эллипсоиде со шкалой по постоянному центральному меридиану в . Изомасштабные линии представляют собой слегка изогнутые линии примерно в 180 км к востоку и западу от центрального меридиана. Максимальное значение масштабного коэффициента составляет 1,001 для UTM и 1,0007 для OSGB. ${\displaystyle k_{0}=0.9996}$ ${\displaystyle k=1}$

Линии единичного масштаба на широте (север и юг), где цилиндрическая поверхность проекции пересекает сферу, являются стандартными параллелями секущей проекции. ${\displaystyle \varphi _{1}}$

Хотя узкая полоса важна для высокоточного картографирования в большом масштабе, для карт мира используются стандартные параллели с гораздо более широким интервалом для управления изменением масштаба. Примеры: ${\displaystyle |k-1|<0.0004}$

• Берманн со стандартными параллелями на 30N, 30S.
• Галл равной площади со стандартными параллелями на 45N, 45S.

Вариант масштаба для равновеликих проекций Ламберта (зеленый) и Галла (красный).

Масштабные графики для последнего показаны ниже в сравнении с масштабными коэффициентами равной площади Ламберта. В последнем случае экватор представляет собой единую стандартную параллель, а масштаб параллели увеличивается от k=1, чтобы компенсировать уменьшение масштаба меридиана. Для Галла параллельный масштаб уменьшен на экваторе (до k=0,707), тогда как масштаб меридиана увеличен (до k=1,414). Это приводит к грубому искажению формы в проекции Галла-Питерса. (На земном шаре длина Африки примерно равна ее ширине). Обратите внимание, что меридианный и параллельный масштабы равны единице на стандартных параллелях.

Математическое приложение

Бесконечно малые элементы на сфере и нормальная цилиндрическая проекция.

Для нормальных цилиндрических проекций геометрия бесконечно малых элементов дает

${\displaystyle {\text{(a)}}\quad \tan \alpha ={\frac {a\cos \varphi \,\delta \lambda }{a\,\delta \varphi }},}$

${\displaystyle {\text{(b)}}\quad \tan \beta ={\frac {\delta x}{\delta y}}={\frac {a\,\delta \lambda }{\delta y}}.}$

Связь между углами и равна ${\displaystyle \beta }$ ${\displaystyle \alpha }$

${\displaystyle {\text{(c)}}\quad \tan \beta ={\frac {a\sec \varphi }{y'(\varphi )}}\tan \alpha .\,}$

Для проекции Меркатора : углы сохраняются. (Неудивительно, поскольку это соотношение используется для вывода Меркатора). Для эквидистантной проекции и проекции Ламберта мы имеем соответственно соотношение между и зависит от широты  . Обозначим масштаб точки в точке P, когда бесконечно малый элемент PQ образует угол с меридианом, через. Он определяется соотношением расстояний: ${\displaystyle y'(\varphi )=a\sec \varphi }$ ${\displaystyle \alpha =\beta }$ ${\displaystyle y'(\varphi )=a}$ ${\displaystyle y'(\varphi )=a\cos \varphi }$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \varphi }$ ${\displaystyle \alpha \,}$ ${\displaystyle \mu _{\alpha }.}$

${\displaystyle \mu _{\alpha }=\lim _{Q\to P}{\frac {P'Q'}{PQ}}=\lim _{Q\to P}{\frac {\sqrt {\delta x^{2}+\delta y^{2}}}{\sqrt {a^{2}\,\delta \varphi ^{2}+a^{2}\cos ^{2}\varphi \,\delta \lambda ^{2}}}}.}$

Установка и замена и из уравнений (a) и (b) соответственно дает ${\displaystyle \delta x=a\,\delta \lambda }$ ${\displaystyle \delta \varphi }$ ${\displaystyle \delta y}$

${\displaystyle \mu _{\alpha }(\varphi )=\sec \varphi \left[{\frac {\sin \alpha }{\sin \beta }}\right].}$

Для проекций, отличных от Меркатора, мы должны сначала выполнить расчеты с использованием уравнения (c), прежде чем мы сможем найти . Например, равнопрямоугольная проекция такова, что ${\displaystyle \beta }$ ${\displaystyle \alpha }$ ${\displaystyle \varphi }$ ${\displaystyle \mu _{\alpha }}$ ${\displaystyle y'=a}$

${\displaystyle \tan \beta =\sec \varphi \tan \alpha .\,}$

Если мы рассмотрим линию постоянного наклона на проекции, то соответствующее значение и масштабный коэффициент вдоль линии являются сложными функциями . Не существует простого способа перенести общее конечное разделение на линейчатую шкалу и получить значимые результаты. ${\displaystyle \beta }$ ${\displaystyle \alpha }$ ${\displaystyle \varphi }$

Символ соотношения

Хотя двоеточие часто используется для выражения отношений, в Юникоде можно использовать символ, специфичный для отношений, слегка приподнятый: U+ 2236 ∶ RATIO ( ∶ ).

Смотрите также

• Географическое расстояние
• Масштаб (аналитический инструмент)
• Масштаб (соотношение)
• Масштабирование (геометрия)
• Пространственный масштаб
• О точности в науке

Примечания

1. Текст «1 см = 6 км» является неправильным обозначением знака равенства ; строго, 1  см = 0,00001  км, согласно определению метрических префиксов .

Рекомендации

1. Снайдер, Джон П. (1987). Картографические проекции - Рабочее руководство. Профессиональный документ Геологической службы США 1395 . Типография правительства США, Вашингтон, округ КолумбияЭтот документ можно скачать со страниц Геологической службы США. Он дает полную информацию о большинстве прогнозов вместе с вводными разделами, но не выводит ни один из прогнозов из основных принципов. Вывод всех формул для проекций Меркатора можно найти в книге «Проекции Меркатора» .
2. Выравнивание Земли: две тысячи лет картографических проекций , Джон П. Снайдер, 1993, стр. 5-8, ISBN 0-226-76747-7 . Это обзор практически всех известных прогнозов с древности до 1993 года. 
3. Селин, Хелейн (2008). Энциклопедия истории науки, техники и медицины в незападных культурах . Спрингер (опубликовано 17 марта 2008 г.). п. 567. ИСБН 978-1402049606.
4. Осборн, Питер (2013), Проекции Меркатора , doi : 10.5281/zenodo.35392. (Дополнения: файлы Maxima, коды и рисунки Latex) {{citation}}: Внешняя ссылка |postscript=( помощь )CS1 maint: postscript (link)
5. Примеры индикатрисы Тиссо. Некоторые иллюстрации Tissot Indicatrix применимы к различным проекциям, отличным от обычных цилиндрических.
6. Дополнительные примеры индикатрисы Тиссо на Wikimedia Commons.