Вращательная спектроскопия

Спектроскопия квантованных вращательных состояний газов

Часть вращательного спектра трифториодометана , CF
₃I . ^{[примечания 1]} Каждый вращательный переход обозначен квантовыми числами J конечного и начального состояний и в значительной степени расщепляется эффектами ядерного квадрупольного взаимодействия с ядром ¹²⁷ I.

Вращательная спектроскопия занимается измерением энергий переходов между квантованными вращательными состояниями молекул в газовой фазе . Вращательный спектр ( спектральная плотность мощности в зависимости от частоты вращения ) полярных молекул может быть измерен в поглощении или излучении с помощью микроволновой спектроскопии ^[1] или с помощью дальней инфракрасной спектроскопии. Вращательные спектры неполярных молекул не могут быть обнаружены этими методами, но могут быть обнаружены и измерены с помощью спектроскопии Рамана . Вращательную спектроскопию иногда называют чистой вращательной спектроскопией, чтобы отличить ее от вращательно-колебательной спектроскопии, где изменения вращательной энергии происходят вместе с изменениями колебательной энергии, а также от ровибронной спектроскопии (или просто вибронной спектроскопии ), где изменения вращательной, колебательной и электронной энергии происходят одновременно.

Для вращательной спектроскопии молекулы классифицируются в соответствии с симметрией на сферические волчки, линейные молекулы и симметричные волчки; аналитические выражения могут быть выведены для терминов вращательной энергии этих молекул. Аналитические выражения могут быть выведены для четвертой категории, асимметричной волчки, для вращательных уровней до J=3, но более высокие уровни энергии необходимо определять с помощью численных методов. Вращательные энергии выводятся теоретически, рассматривая молекулы как жесткие роторы , а затем применяя дополнительные члены для учета центробежного искажения , тонкой структуры , сверхтонкой структуры и кориолисовой связи . Подгонка спектров к теоретическим выражениям дает численные значения угловых моментов инерции , из которых в благоприятных случаях могут быть выведены очень точные значения длин и углов молекулярных связей. В присутствии электростатического поля происходит расщепление Штарка , которое позволяет определять молекулярные электрические дипольные моменты .

Важным применением вращательной спектроскопии является исследование химического состава межзвездной среды с помощью радиотелескопов .

Приложения

Вращательная спектроскопия в первую очередь использовалась для исследования фундаментальных аспектов молекулярной физики. Это уникальный точный инструмент для определения молекулярной структуры в молекулах газовой фазы. Он может быть использован для установления барьеров для внутреннего вращения, например, связанного с вращением CH
₃группа относительно C
₆ЧАС
₄Группа Cl в хлортолуоле ( C
₇ЧАС
₇Cl ). ^[2] Когда можно наблюдать тонкую или сверхтонкую структуру, этот метод также дает информацию об электронных структурах молекул. Большая часть современного понимания природы слабых молекулярных взаимодействий, таких как связи Ван-дер-Ваальса , водорода и галогенов, была установлена ​​с помощью вращательной спектроскопии. В связи с радиоастрономией этот метод играет ключевую роль в исследовании химического состава межзвездной среды . Микроволновые переходы измеряются в лаборатории и сопоставляются с излучением межзвездной среды с помощью радиотелескопа . NH3была первой стабильной многоатомной молекулой, идентифицированной в межзвездной среде . ^[3] Измерение оксида хлора ^[4] важно для химии атмосферы . Текущие проекты в области астрохимии включают как лабораторную микроволновую спектроскопию, так и наблюдения, проводимые с использованием современных радиотелескопов, таких как Atacama Large Millimeter/submillimeter Array (ALMA). ^[5]

Обзор

Молекула в газовой фазе может свободно вращаться относительно набора взаимно ортогональных осей фиксированной ориентации в пространстве, центрированных на центре масс молекулы. Свободное вращение невозможно для молекул в жидкой или твердой фазах из-за наличия межмолекулярных сил . Вращение вокруг каждой уникальной оси связано с набором квантованных уровней энергии, зависящих от момента инерции относительно этой оси и квантового числа. Таким образом, для линейных молекул уровни энергии описываются одним моментом инерции и одним квантовым числом, , которое определяет величину вращательного углового момента. ${\displaystyle J}$

Для нелинейных молекул, которые являются симметричными роторами (или симметричными волчками - см. следующий раздел), существуют два момента инерции, а энергия также зависит от второго вращательного квантового числа, , которое определяет векторную составляющую вращательного углового момента вдоль главной оси симметрии . ^[6] Анализ спектроскопических данных с помощью выражений, подробно описанных ниже, приводит к количественному определению значения(й) момента(ов) инерции. Из этих точных значений молекулярной структуры и размеров могут быть получены. ${\displaystyle K}$

Для линейной молекулы анализ вращательного спектра дает значения для вращательной постоянной ^{[примечания 2]} и момента инерции молекулы, и, зная атомные массы, может быть использован для непосредственного определения длины связи . Для двухатомных молекул этот процесс прост. Для линейных молекул с более чем двумя атомами необходимо измерить спектры двух или более изотопологов , таких как ¹⁶ O ¹² C ³² S и ¹⁶ O ¹² C ³⁴ S. Это позволяет составить и решить набор одновременных уравнений для длин связей ). ^{[примечания 3]} Длина связи, полученная таким образом, немного отличается от равновесной длины связи. Это связано с тем, что в основном колебательном состоянии, к которому относятся вращательные состояния, имеется нулевая энергия , тогда как равновесная длина связи находится в минимуме на кривой потенциальной энергии. Соотношение между вращательными постоянными задается выражением

${\displaystyle B_{v}=B-\alpha \left(v+{\frac {1}{2}}\right)}$

где v — колебательное квантовое число, а α — константа взаимодействия колебания и вращения, которую можно вычислить, если найти значения B для двух различных колебательных состояний. ^[7]

Для других молекул, если спектры могут быть разрешены и отдельные переходы, назначенные как длинам связей , так и углам связей, могут быть выведены. Когда это невозможно, как в случае большинства асимметричных вершин, все, что можно сделать, это подогнать спектры к трем моментам инерции, рассчитанным из предполагаемой молекулярной структуры. Изменяя молекулярную структуру, можно улучшить соответствие, что даст качественную оценку структуры. Изотопное замещение бесценно при использовании этого подхода к определению молекулярной структуры.

Классификация молекулярных роторов

В квантовой механике свободное вращение молекулы квантуется , так что энергия вращения и момент импульса могут принимать только определенные фиксированные значения, которые просто связаны с моментом инерции , , молекулы. Для любой молекулы существует три момента инерции: , и около трех взаимно ортогональных осей A , B , и C с началом в центре масс системы. Общее соглашение, используемое в этой статье, заключается в определении осей таким образом, что , с осью, соответствующей наименьшему моменту инерции. Некоторые авторы, однако, определяют ось как ось вращения молекулы наивысшего порядка. ${\displaystyle I}$ ${\displaystyle I_{A}}$ ${\displaystyle I_{B}}$ ${\displaystyle I_{C}}$ ${\displaystyle I_{A}\leq I_{B}\leq I_{C}}$ ${\displaystyle A}$ ${\displaystyle A}$

Конкретный рисунок энергетических уровней (и, следовательно, переходов во вращательном спектре) для молекулы определяется ее симметрией. Удобный способ рассмотреть молекулы — разделить их на четыре различных класса, основанных на симметрии их структуры. Это

Сферические верхушки (сферические роторы)

Все три момента инерции равны друг другу: . Примерами сферических волчков являются тетрамер фосфора ( P ${\displaystyle I_{A}=I_{B}=I_{C}}$4) , четыреххлористый углерод ( CCl
₄) и другие тетрагалогениды, метан ( CH
₄) , силан, ( SiH
₄) , гексафторид серы ( SF
₆) и другие гексагалогениды. Все молекулы принадлежат к кубическим точечным группам T _d или O _h .

Линейные молекулы

Для линейной молекулы моменты инерции связаны соотношением . Для большинства целей можно принять равным нулю. Примерами линейных молекул являются дикислород ( O ${\displaystyle I_{A}\ll I_{B}=I_{C}}$ ${\displaystyle I_{A}}$2) , диазот ( N
₂) , оксид углерода (CO) , гидроксильный радикал (OH) , диоксид углерода (CO ₂ ) , цианистый водород (HCN) , карбонилсульфид (OCS) , ацетилен (этин (HC≡CH) и дигалогенэтины. Эти молекулы принадлежат к точечным группам C _∞v или D _∞h .

Симметричные волчки (симметричные роторы)

Симметричный волчок — это молекула, в которой два момента инерции одинаковы, или . По определению симметричный волчок должен иметь ось вращения 3-го или более высокого порядка . Для удобства спектроскописты делят молекулы на два класса симметричных волчков: сплющенные симметричные волчки (в форме блюдца или диска) с и вытянутые симметричные волчки (в форме регбийного мяча или сигары) с . Спектры выглядят довольно по-разному и мгновенно распознаются. Примерами симметричных волчков являются ${\displaystyle I_{A}=I_{B}}$ ${\displaystyle I_{B}=I_{C}}$ ${\displaystyle I_{A}=I_{B}<I_{C}}$ ${\displaystyle I_{A}<I_{B}=I_{C}}$

сплющенный

Бензол, С
₆ЧАС
₆; аммиак, NH
₃; тетрафторид ксенона, XeF
₄

Вытянутый

Хлорметан, CH
₃Cl , пропин, CH
₃С≡СН

В качестве подробного примера, аммиак имеет момент инерции I _C = 4,4128 × 10−47 ^кг м ² относительно оси вращения 3-го порядка и моменты I _A = I _B = 2,8059 × 10−47 ^кг м ² относительно любой оси, перпендикулярной оси C _3. Поскольку уникальный момент инерции больше двух других, молекула представляет собой сплющенный симметричный волчок. ^[8]

Асимметричные вершины (асимметричные роторы)

Три момента инерции имеют разные значения. Примерами малых молекул, которые являются асимметричными вершинами, являются вода, H
₂O и диоксид азота, NO
₂ось симметрии которой высшего порядка является осью вращения 2-го порядка. Большинство крупных молекул являются асимметричными вершинами.

Правила отбора

Микроволновый и дальний инфракрасный спектры

Переходы между вращательными состояниями можно наблюдать в молекулах с постоянным электрическим дипольным моментом . ^{[9] [примечания 4]} Следствием этого правила является то, что для центросимметричных линейных молекул, таких как N, не может наблюдаться микроволновый спектр.
₂( динозот ) или HCCH ( этин ), которые неполярны. Тетраэдрические молекулы, такие как CH
₄( метан ), который имеет как нулевой дипольный момент, так и изотропную поляризуемость, не имел бы чисто вращательного спектра, если бы не эффект центробежного искажения; когда молекула вращается вокруг оси симметрии 3-го порядка, создается небольшой дипольный момент, что позволяет наблюдать слабый вращательный спектр с помощью микроволновой спектроскопии. ^[10]

При симметричных вершинах правило отбора для электрических дипольно-разрешенных чистых вращательных переходов Δ K = 0 , Δ J = ±1 . Поскольку эти переходы обусловлены поглощением (или испусканием) одного фотона со спином единица, сохранение углового момента подразумевает, что молекулярный угловой момент может измениться максимум на одну единицу. ^[11] Более того, квантовое число K ограничено значениями между + J и - J включительно . ^[12]

Рамановские спектры

Для спектров Рамана молекулы претерпевают переходы, в которых падающий фотон поглощается, а другой рассеянный фотон испускается. Общее правило отбора для разрешения такого перехода заключается в том, что молекулярная поляризуемость должна быть анизотропной , что означает, что она не одинакова во всех направлениях. ^[13] Поляризуемость — это трехмерный тензор , который можно представить в виде эллипсоида. Эллипсоид поляризуемости сферических молекул на самом деле сферический, поэтому эти молекулы не показывают вращательного спектра Рамана. Для всех других молекул можно наблюдать как стоксовы , так и антистоксовы линии ^{[примечания 5]} , и они имеют схожую интенсивность из-за того, что многие вращательные состояния термически заселены. Правило отбора для линейных молекул — ΔJ = 0, ±2. Причина значений ±2 заключается в том, что поляризуемость дважды возвращается к одному и тому же значению во время вращения. ^[14] Значение ΔJ = 0 соответствует не молекулярному переходу, а скорее рэлеевскому рассеянию , при котором падающий фотон просто меняет направление. ^[15]

Правило отбора для молекул с симметричным верхом:

ΔК = 0

Если К = 0, то ΔJ = ±2

Если К ≠ 0, то ΔJ = 0, ±1, ±2

Переходы с Δ J = +1 относятся к серии R , тогда как переходы с Δ J = +2 относятся к серии S. ^[15] Поскольку рамановские переходы включают два фотона, молекулярный угловой момент может измениться на две единицы.

Единицы

Единицы, используемые для вращательных констант, зависят от типа измерения. Для инфракрасных спектров в шкале волновых чисел ( ) единицей обычно является обратный сантиметр , записываемый как см ⁻¹ , что буквально означает количество волн в одном сантиметре или обратную величину длины волны в сантиметрах ( ). С другой стороны, для микроволновых спектров в шкале частот ( ) единицей обычно является гигагерц . Связь между этими двумя единицами выводится из выражения ${\displaystyle {\tilde {\nu }}}$ ${\displaystyle {\tilde {\nu }}=1/\lambda }$ ${\displaystyle \nu }$

${\displaystyle \nu \cdot \lambda =c,}$

где ν - частота , λ - длина волны , а c - скорость света . Отсюда следует, что

${\displaystyle {\tilde {\nu }}/{\text{cm}}^{-1}={\frac {1}{\lambda /{\text{cm}}}}={\frac {\nu /{\text{s}}^{-1}}{c/\left({\text{cm}}\cdot \mathrm {s} ^{-1}\right)}}={\frac {\nu /{\text{s}}^{-1}}{2.99792458\times 10^{10}}}.}$

Поскольку 1 ГГц = 10 ⁹ Гц, числовое преобразование можно выразить как

${\displaystyle {\tilde {\nu }}/{\text{cm}}^{-1}\approx {\frac {\nu /{\text{GHz}}}{30}}.}$

Влияние вибрации на вращение

Заселение колебательно-возбужденных состояний следует распределению Больцмана , поэтому низкочастотные колебательные состояния заметно заселены даже при комнатных температурах. Поскольку момент инерции выше, когда колебание возбуждено, вращательные константы ( B ) уменьшаются. Следовательно, частоты вращения в каждом колебательном состоянии отличаются друг от друга. Это может привести к появлению «спутниковых» линий во вращательном спектре. Примером может служить цианодиацетилен , H−C≡C−C≡C−C≡N. ^[16]

Далее, существует фиктивная сила , связь Кориолиса , между колебательным движением ядер во вращающейся (неинерциальной) системе отсчета. Однако, пока колебательное квантовое число не меняется (т. е. молекула находится только в одном состоянии колебания), влияние вибрации на вращение неважно, поскольку время для вибрации намного короче времени, необходимого для вращения. Связь Кориолиса часто также пренебрежимо мала, если интересуют только низкие колебательные и вращательные квантовые числа.

Влияние вращения на колебательные спектры

Исторически теория уровней вращательной энергии была разработана для учета наблюдений спектров колебания-вращения газов в инфракрасной спектроскопии , которая использовалась до того, как микроволновая спектроскопия стала практической. В первом приближении вращение и вибрация могут рассматриваться как разделимые , поэтому энергия вращения добавляется к энергии вибрации. Например, уровни вращательной энергии для линейных молекул (в приближении жесткого ротора) имеют вид

${\displaystyle E_{\text{rot}}=hcBJ(J+1).}$

В этом приближении колебательно-вращательные волновые числа переходов равны

${\displaystyle {\tilde {\nu }}={\tilde {\nu }}_{\text{vib}}+B''J''(J''+1)-B'J'(J'+1),}$

где и являются вращательными константами для верхнего и нижнего колебательного состояния соответственно, в то время как и являются вращательными квантовыми числами верхнего и нижнего уровней. В действительности, это выражение должно быть изменено для эффектов ангармоничности колебаний, для центробежного искажения и для связи Кориолиса. ^[17] ${\displaystyle B''}$ ${\displaystyle B'}$ ${\displaystyle J''}$ ${\displaystyle J'}$

Для так называемой ветви R спектра, так что происходит одновременное возбуждение как вибрации, так и вращения. Для ветви P , так что квант вращательной энергии теряется, в то время как квант колебательной энергии приобретается. Чисто колебательный переход, , дает начало ветви Q спектра. Из-за термической заселенности вращательных состояний ветвь P немного менее интенсивна, чем ветвь R. ${\displaystyle J'=J''+1}$ ${\displaystyle J'=J''-1}$ ${\displaystyle \Delta J=0}$

Константы вращения, полученные с помощью инфракрасных измерений, хорошо согласуются с константами, полученными с помощью микроволновой спектроскопии, при этом последняя обычно обеспечивает большую точность.

Структура вращательных спектров

Сферическая вершина

Сферические волчки не имеют чистого дипольного момента. Чистый вращательный спектр не может быть обнаружен с помощью абсорбционной или эмиссионной спектроскопии, поскольку не существует постоянного дипольного момента, вращение которого может быть ускорено электрическим полем падающего фотона. Кроме того, поляризуемость изотропна, поэтому чистые вращательные переходы также не могут быть обнаружены с помощью рамановской спектроскопии. Тем не менее, вращательные константы могут быть получены с помощью вращательно-колебательной спектроскопии . Это происходит, когда молекула полярна в колебательно-возбужденном состоянии. Например, молекула метана представляет собой сферический волчок, но асимметричная полоса растяжения CH показывает вращательную тонкую структуру в инфракрасном спектре, проиллюстрированную вращательно-колебательной связью . Этот спектр также интересен, поскольку он демонстрирует явные доказательства связи Кориолиса в асимметричной структуре полосы.

Линейные молекулы

Уровни энергии и положения линий, рассчитанные в приближении жесткого ротора

Жесткий ротор является хорошей отправной точкой для построения модели вращающейся молекулы. Предполагается, что атомы-компоненты являются точечными массами , соединенными жесткими связями. Линейная молекула лежит на одной оси, и каждый атом движется по поверхности сферы вокруг центра масс. Две степени свободы вращения соответствуют сферическим координатам θ и φ, которые описывают направление молекулярной оси, а квантовое состояние определяется двумя квантовыми числами J и M. J определяет величину вращательного момента импульса, а M — его компоненту относительно оси, фиксированной в пространстве, такой как внешнее электрическое или магнитное поле. При отсутствии внешних полей энергия зависит только от J. В модели жесткого ротора уровни вращательной энергии F (J) молекулы можно выразить как,

${\displaystyle F\left(J\right)=BJ\left(J+1\right)\qquad J=0,1,2,...}$

где - вращательная постоянная молекулы и связана с моментом инерции молекулы. В линейной молекуле момент инерции относительно оси, перпендикулярной молекулярной оси, является уникальным, то есть, , поэтому ${\displaystyle B}$ ${\displaystyle I_{B}=I_{C},I_{A}=0}$

${\displaystyle B={h \over {8\pi ^{2}cI_{B}}}={h \over {8\pi ^{2}cI_{C}}}}$

Для двухатомной молекулы

${\displaystyle I={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}d^{2}}$

где m ₁ и m ₂ — массы атомов, а d — расстояние между ними.

Правила отбора диктуют, что во время испускания или поглощения вращательное квантовое число должно измениться на единицу, т. е . Таким образом, расположение линий во вращательном спектре будет определяться выражением ${\displaystyle \Delta J=J^{\prime }-J^{\prime \prime }=\pm 1}$

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime }}=F\left(J^{\prime }\right)-F\left(J^{\prime \prime }\right)=2B\left(J^{\prime \prime }+1\right)\qquad J^{\prime \prime }=0,1,2,...}$

где обозначает нижний уровень, а обозначает верхний уровень, участвующий в переходе. ${\displaystyle J^{\prime \prime }}$ ${\displaystyle J^{\prime }}$

Диаграмма иллюстрирует вращательные переходы, которые подчиняются правилу отбора =1. Пунктирные линии показывают, как эти переходы отображаются на особенности, которые можно наблюдать экспериментально. Соседние переходы разделены 2 B в наблюдаемом спектре. Единицы частоты или волнового числа также могут использоваться для оси x этого графика. ${\displaystyle \Delta J}$ ${\displaystyle J^{\prime \prime }{\leftarrow }J^{\prime }}$

Интенсивность вращательных линий

Заселенности вращательных уровней с Bhc / kT = 0,05. J — квантовое число нижнего вращательного состояния.

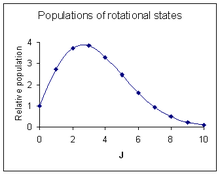
Вероятность перехода является наиболее важным фактором, влияющим на интенсивность наблюдаемой вращательной линии. Эта вероятность пропорциональна населению начального состояния, вовлеченного в переход. Население вращательного состояния зависит от двух факторов. Число молекул в возбужденном состоянии с квантовым числом J относительно числа молекул в основном состоянии, N _J / N _{0 ,} определяется распределением Больцмана как

${\displaystyle {\frac {N_{J}}{N_{0}}}=e^{-{\frac {E_{J}}{kT}}}=e^{-{\frac {BhcJ(J+1)}{kT}}}}$,

где k — постоянная Больцмана , а T — абсолютная температура . Этот фактор уменьшается с ростом J. Второй фактор — вырождение вращательного состояния, равное 2J + 1. Этот фактор увеличивается с ростом J. Объединяя два фактора ^[18]

${\displaystyle {\text{population}}\propto (2J+1)e^{-{\frac {E_{J}}{kT}}}}$

Максимальная относительная интенсивность наблюдается при ^{[19] [примечания 6]}

${\displaystyle J={\sqrt {\frac {kT}{2hcB}}}-{\frac {1}{2}}}$

На диаграмме справа показана картина интенсивности, примерно соответствующая спектру над ней.

Центробежное искажение

Когда молекула вращается, центробежная сила раздвигает атомы. В результате момент инерции молекулы увеличивается, тем самым уменьшая значение , когда оно вычисляется с использованием выражения для жесткого ротора. Чтобы учесть это, к уровням вращательной энергии двухатомной молекулы добавляется поправочный член центробежного искажения. ^[20] ${\displaystyle B}$

${\displaystyle F\left(J\right)=BJ\left(J+1\right)-DJ^{2}\left(J+1\right)^{2}\qquad J=0,1,2,...}$

где - константа центробежного искажения. ${\displaystyle D}$

Поэтому положение линий для вращательного режима меняется на

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime }}=2B\left(J^{\prime \prime }+1\right)-4D\left(J^{\prime \prime }+1\right)^{3}\qquad J^{\prime \prime }=0,1,2,...}$

В результате расстояние между линиями не является постоянным, как в приближении жесткого ротора, а уменьшается с увеличением вращательного квантового числа.

Предположение, лежащее в основе этих выражений, заключается в том, что молекулярная вибрация следует простому гармоническому движению . В гармоническом приближении центробежная постоянная может быть выведена как ${\displaystyle D}$

${\displaystyle D={\frac {h^{3}}{32\pi ^{4}I^{2}r^{2}kc}}}$

где k — константа колебательной силы . Связь между и ${\displaystyle B}$ ${\displaystyle D}$

${\displaystyle D={\frac {4B^{3}}{{\tilde {\omega }}^{2}}}}$

где - частота гармонических колебаний, следует. Если необходимо учесть ангармоничность, то к выражениям для уровней энергии и положений линий следует добавить члены в более высоких степенях J. ^[20] Яркий пример касается вращательного спектра фтористого водорода , который был подобран к членам до [J(J+1)] ⁵ . ^[21] ${\displaystyle {\tilde {\omega }}}$

Кислород

Электрический дипольный момент молекулы дикислорода, O
₂равен нулю, но молекула является парамагнитной с двумя неспаренными электронами, так что существуют магнитно-дипольные разрешенные переходы, которые можно наблюдать с помощью микроволновой спектроскопии. Спин единичного электрона имеет три пространственные ориентации относительно заданного вектора вращательного момента молекулы, K, так что каждый вращательный уровень расщепляется на три состояния, J = K + 1, K и K - 1, каждое состояние J этого так называемого триплета p-типа возникает из-за различной ориентации спина относительно вращательного движения молекулы. Разница энергий между последовательными членами J в любом из этих триплетов составляет около 2 см ⁻¹ (60 ГГц), за единственным исключением разницы J = 1←0, которая составляет около 4 см ⁻¹ . Правила отбора для магнитно-дипольных переходов допускают переходы между последовательными членами триплета (ΔJ = ±1), так что для каждого значения квантового числа вращательного момента K существует два разрешенных перехода. Ядро ¹⁶ O имеет нулевой ядерный спиновый угловой момент, поэтому соображения симметрии требуют, чтобы K имел только нечетные значения. ^{[22] [23]}

Симметричный верх

Для симметричных роторов квантовое число J связано с полным угловым моментом молекулы. Для заданного значения J существует 2 J +1-кратное вырождение с квантовым числом M , принимающим значения + J ...0 ... - J . Третье квантовое число K связано с вращением вокруг главной оси вращения молекулы. При отсутствии внешнего электрического поля энергия вращения симметричного волчка является функцией только J и K, и в приближении жесткого ротора энергия каждого вращательного состояния определяется выражением

${\displaystyle F\left(J,K\right)=BJ\left(J+1\right)+\left(A-B\right)K^{2}\qquad J=0,1,2,\ldots \quad {\mbox{and}}\quad K=+J,\ldots ,0,\ldots ,-J}$

где и для вытянутой симметричной волчковой молекулы или для сплющенной молекулы. ${\displaystyle B={h \over {8\pi ^{2}cI_{B}}}}$ ${\displaystyle A={h \over {8\pi ^{2}cI_{A}}}}$ ${\displaystyle A={h \over {8\pi ^{2}cI_{C}}}}$

Это дает волновые числа перехода как

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime },K}=F\left(J^{\prime },K\right)-F\left(J^{\prime \prime },K\right)=2B\left(J^{\prime \prime }+1\right)\qquad J^{\prime \prime }=0,1,2,...}$

что то же самое, что и в случае линейной молекулы. ^[24] С поправкой первого порядка на центробежное искажение волновые числа перехода становятся

${\displaystyle {\tilde {\nu }}_{J^{\prime }\leftrightarrow J^{\prime \prime },K}=F\left(J^{\prime },K\right)-F\left(J^{\prime \prime },K\right)=2\left(B-2D_{JK}K^{2}\right)\left(J^{\prime \prime }+1\right)-4D_{J}\left(J^{\prime \prime }+1\right)^{3}\qquad J^{\prime \prime }=0,1,2,...}$

Член в D _JK устраняет вырождение, присутствующее в приближении жесткого ротора, с различными значениями K. ^[25]

Асимметричный верх

Спектр чистого вращения атмосферного водяного пара, измеренный на Мауна-Кеа (от 33 см ⁻¹ до 100 см ⁻¹ )

Квантовое число J относится к полному угловому моменту, как и прежде. Поскольку есть три независимых момента инерции, есть два других независимых квантовых числа, которые следует рассмотреть, но значения терминов для асимметричного ротора не могут быть получены в замкнутой форме. Они получаются путем индивидуальной матричной диагонализации для каждого значения J. Формулы доступны для молекул, форма которых приближается к форме симметричного волчка. ^[26]

Молекула воды является важным примером асимметричного волчка. Она имеет интенсивный спектр чистого вращения в дальней инфракрасной области, ниже примерно 200 см ⁻¹ . По этой причине спектрометры дальней инфракрасной области должны быть освобождены от атмосферного водяного пара либо путем продувки сухим газом, либо путем вакуумирования. Спектр был подробно проанализирован. ^[27]

Квадрупольное расщепление

Когда ядро ​​имеет спиновое квантовое число I больше 1/2, оно имеет квадрупольный момент. В этом случае связь ядерного спинового углового момента с вращательным угловым моментом вызывает расщепление уровней вращательной энергии. Если квантовое число J вращательного уровня больше I , образуются 2 уровня I + 1 ; но если J меньше I , образуются 2 уровня J + 1. Эффект представляет собой один из типов сверхтонкого расщепления . Например, при ¹⁴ N ( I = 1 ) в HCN все уровни с J > 0 расщепляются на 3. Энергии подуровней пропорциональны ядерному квадрупольному моменту и являются функцией F и J. где F = J + I , J + I − 1, …, | J − I | . Таким образом, наблюдение ядерного квадрупольного расщепления позволяет определить величину ядерного квадрупольного момента. ^[28] Это альтернативный метод использования ядерной квадрупольной резонансной спектроскопии. Правило отбора для вращательных переходов становится ^[29]

${\displaystyle \Delta J=\pm 1,\Delta F=0,\pm 1}$

Эффекты Штарка и Зеемана

В присутствии статического внешнего электрического поля вырождение 2 J + 1 каждого вращательного состояния частично снимается, пример эффекта Штарка . Например, в линейных молекулах каждый уровень энергии расщепляется на J + 1 компонент. Степень расщепления зависит от квадрата напряженности электрического поля и квадрата дипольного момента молекулы. ^[30] В принципе это дает возможность определить значение молекулярного дипольного момента с высокой точностью. Примерами являются карбонилсульфид , OCS, с μ = 0,71521 ± 0,00020 дебая . Однако, поскольку расщепление зависит от μ ² , ориентация диполя должна быть выведена из квантово-механических соображений. ^[31]

Аналогичное снятие вырождения произойдет, если парамагнитную молекулу поместить в магнитное поле, пример эффекта Зеемана . Большинство видов, которые можно наблюдать в газообразном состоянии, являются диамагнитными . Исключения составляют молекулы с нечетными электронами, такие как оксид азота , NO, диоксид азота , NO
₂, некоторые оксиды хлора и гидроксильный радикал . Эффект Зеемана наблюдался с дикислородом , O
₂^[32]

Вращательная Рамановская спектроскопия

Молекулярные вращательные переходы также можно наблюдать с помощью спектроскопии комбинационного рассеяния . Вращательные переходы разрешены комбинационным рассеянием для любой молекулы с анизотропной поляризуемостью , которая включает все молекулы, за исключением сферических вершин. Это означает, что вращательные переходы молекул без постоянного дипольного момента, которые нельзя наблюдать при поглощении или испускании, можно наблюдать с помощью рассеяния в спектроскопии комбинационного рассеяния. Спектры комбинационного рассеяния очень высокого разрешения можно получить, адаптировав инфракрасный спектрометр с преобразованием Фурье . Примером может служить спектр¹⁵
Н
₂. Он показывает эффект ядерного спина, приводящий к изменению интенсивности в соотношении 3:1 в соседних линиях. Из данных была выведена длина связи 109,9985 ± 0,0010 пм. ^[33]

Инструменты и методы

Подавляющее большинство современных спектрометров используют смесь коммерчески доступных и заказных компонентов, которые пользователи интегрируют в соответствии со своими конкретными потребностями. Приборы можно широко классифицировать в соответствии с их общими принципами работы. Хотя вращательные переходы можно обнаружить в очень широкой области электромагнитного спектра , существуют фундаментальные физические ограничения на рабочую полосу пропускания компонентов прибора. Часто непрактично и дорого переключаться на измерения в совершенно другой области частот. Приборы и принципы работы, описанные ниже, в целом подходят для экспериментов по микроволновой спектроскопии, проводимых на частотах от 6 до 24 ГГц.

Ячейки поглощения и модуляция Штарка

Микроволновый спектрометр может быть наиболее просто сконструирован с использованием источника микроволнового излучения, ячейки поглощения, в которую может быть введен образец газа, и детектора, такого как супергетеродинный приемник . Спектр может быть получен путем сканирования частоты источника при обнаружении интенсивности прошедшего излучения. Простая секция волновода может служить ячейкой поглощения. Важная вариация метода, в котором переменный ток подается через электроды внутри ячейки поглощения, приводит к модуляции частот вращательных переходов. Это называется модуляцией Штарка и позволяет использовать фазочувствительные методы обнаружения, предлагающие улучшенную чувствительность. Абсорбционная спектроскопия позволяет изучать образцы, которые термодинамически стабильны при комнатной температуре. Первое исследование микроволнового спектра молекулы ( NH
₃) был выполнен Клитоном и Уильямсом в 1934 году. ^[34] Последующие эксперименты использовали мощные источники микроволн, такие как клистрон , многие из которых были разработаны для радаров во время Второй мировой войны . Количество экспериментов в области микроволновой спектроскопии резко возросло сразу после войны. К 1948 году Уолтер Горди смог подготовить обзор результатов, содержащихся примерно в 100 научных работах. ^[35] Коммерческие версии ^[36] микроволнового абсорбционного спектрометра были разработаны Hewlett-Packard в 1970-х годах и когда-то широко использовались для фундаментальных исследований. Большинство исследовательских лабораторий теперь используют либо спектрометры Балле- Флигара , либо микроволновые спектрометры с преобразованием Фурье с чирпированным импульсом (FTMW).

Фурье-преобразование микроволновой спектроскопии (FTMW)

Теоретическая структура ^[37], лежащая в основе спектроскопии FTMW, аналогична той, которая используется для описания спектроскопии FT-NMR . Поведение развивающейся системы описывается оптическими уравнениями Блоха . Во-первых, короткий (обычно длительностью 0-3 микросекунды) микроволновый импульс вводится в резонанс с вращательным переходом. Те молекулы, которые поглощают энергию из этого импульса, заставляют вращаться когерентно в фазе с падающим излучением. За дезактивацией импульса поляризации следует микроволновое излучение, которое сопровождает декогеренцию молекулярного ансамбля. Этот спад свободной индукции происходит в масштабе времени 1-100 микросекунд в зависимости от настроек прибора. После пионерской работы Дике и его коллег в 1950-х годах ^[38] первый спектрометр FTMW был построен Эккерсом и Флайгаром в 1975 году. ^[39]

FTMW-спектрометр Балле – Флайгара

Балле, Кэмпбелл, Кинан и Флайгар продемонстрировали, что метод FTMW может применяться в «ячейке свободного пространства», включающей вакуумированную камеру, содержащую полость Фабри-Перо . ^[40] Этот метод позволяет исследовать образец всего через миллисекунды после того, как он быстро охлаждается всего до нескольких кельвинов в горловине расширяющейся газовой струи. Это было революционное достижение, поскольку (i) охлаждение молекул до низких температур концентрирует имеющуюся популяцию на самых низких уровнях вращательной энергии. В сочетании с преимуществами, предоставляемыми использованием полости Фабри-Перо, это принесло значительное повышение чувствительности и разрешения спектрометров наряду с уменьшением сложности наблюдаемых спектров; (ii) стало возможным изолировать и изучать молекулы, которые очень слабо связаны, поскольку для них недостаточно энергии, чтобы подвергнуться фрагментации или химической реакции при таких низких температурах. Уильям Клемперер был пионером в использовании этого инструмента для исследования слабосвязанных взаимодействий. В то время как полость Фабри-Перо спектрометра Balle-Flygare FTMW обычно может быть настроена на резонанс на любой частоте от 6 до 18 ГГц, полоса пропускания отдельных измерений ограничена примерно 1 МГц. Анимация иллюстрирует работу этого инструмента, который в настоящее время является наиболее широко используемым инструментом для микроволновой спектроскопии. ^[41]

Спектрометр с чирпированным импульсом FTMW

Отметив, что цифровые преобразователи и связанные с ними электронные технологии значительно продвинулись с момента появления FTMW-спектроскопии, Б. Х. Пейт из Университета Вирджинии ^[42] спроектировал спектрометр ^[43] , который сохраняет многие преимущества спектрометра Balle-Flygare FT-MW, в то же время внедряя инновации в (i) использовании высокоскоростного (>4 Гвыб/с) генератора произвольных сигналов для генерации «чирпированного» микроволнового поляризационного импульса, который распространяется до 12 ГГц по частоте менее чем за микросекунду, и (ii) использовании высокоскоростного (>40 Гвыб/с) осциллографа для оцифровки и преобразования Фурье распада молекулярной свободной индукции. Результатом является прибор, который позволяет изучать слабосвязанные молекулы, но который способен использовать полосу пропускания измерений (12 ГГц), которая значительно расширена по сравнению со спектрометром Balle-Flygare FTMW. Модифицированные версии оригинального спектрометра CP-FTMW были созданы рядом групп в Соединенных Штатах, Канаде и Европе. ^{[44] [45]} Прибор обеспечивает широкополосную возможность, которая в значительной степени дополняет высокую чувствительность и разрешение, предлагаемые конструкцией Балле-Флигара.

Примечания

1. Спектр измерялся в течение нескольких часов с помощью микроволнового спектрометра с преобразованием Фурье и чирпированным импульсом в Университете Бристоля.
2. В этой статье используется соглашение молекулярных спектроскопистов о выражении вращательной постоянной в см ⁻¹ . Поэтому в этой статье соответствует статье о жестком роторе. ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle {\bar {B}}=B/hc}$
3. Для симметричного волчка значения 2 моментов инерции могут быть использованы для получения 2 молекулярных параметров. Значения от каждого дополнительного изотополога предоставляют информацию для еще одного молекулярного параметра. Для асимметричных волчков один изотополог предоставляет информацию для максимум 3 молекулярных параметров.
4. Такие переходы называются электрическими дипольно-разрешенными переходами. Другие переходы, включающие квадруполи, октуполи, гексадекаполи и т. д., также могут быть разрешены, но спектральная интенсивность намного меньше, поэтому эти переходы трудно наблюдать. Магнитно-дипольно-разрешенные переходы могут происходить в парамагнитных молекулах, таких как дикислород , O
   ₂и оксид азота , NO
5. В Рамановской спектроскопии энергии фотонов для стоксового и антистоксового рассеяния соответственно меньше и больше энергии падающего фотона. См. диаграмму уровней энергии в Рамановской спектроскопии .
6. Это значение J соответствует максимуму популяции, рассматриваемой как непрерывная функция J. Однако, поскольку допускаются только целые значения J, максимальная интенсивность линии наблюдается для соседнего целого значения J.

Ссылки

1. Горди, В. (1970). А. Вайсбергер (ред.). Микроволновые молекулярные спектры в технике органической химии . Т. IX. Нью-Йорк: Interscience.
2. Nair, KPR; Demaison, J.; Wlodarczak, G.; Merke, I. (236). «Вращательный спектр миллиметровых волн и внутреннее вращение в о-хлортолуоле». Журнал молекулярной спектроскопии . 237 (2): 137–142. Bibcode : 2006JMoSp.237..137N. doi : 10.1016/j.jms.2006.03.011.
3. Чунг, AC; Ранк, DM; Таунс, CH; Торнтон, DD и Уэлч, WJ (1968). «Обнаружение NH
   ₃молекул в межзвездной среде по их спектрам микроволнового излучения». Physical Review Letters . 21 (25): 1701–5. Bibcode : 1968PhRvL..21.1701C. doi : 10.1103/PhysRevLett.21.1701.
4. Рико, П.; Барон, П.; де Ла Ноэ, Ж. (2004). «Оценка качества наземных микроволновых измерений оксида хлора, озона и диоксида азота с помощью радиометра NDSC на плато де Бюр». Ann. Geophys . 22 (6): 1903–15. Bibcode : 2004AnGeo..22.1903R. doi : 10.5194/angeo-22-1903-2004 .
5. "Астрохимия в Вирджинии" . Получено 2 декабря 2012 г.
6. Аткинс и де Паула 2006, с. 444
7. Банвелл и Маккэш 1994, стр. 99
8. Значения момента инерции из Atkins & de Paula 2006, стр. 445
9. Холлас 1996, стр. 95
10. Холлас 1996, стр. 104 показывает часть наблюдаемого вращательного спектра силана
11. Аткинс и де Паула 2006, с. 447
12. Банвелл и Маккэш 1994, стр. 49
13. Холлас 1996, стр. 111
14. Аткинс и де Паула 2006, стр. 474–5.
15. Banwell & McCash 1994, Раздел 4.2, стр. 105, Чистые вращательные спектры комбинационного рассеяния
16. Alexander, AJ; Kroto, HW; Walton, DRM (1967). «Микроволновый спектр, структура замещения и дипольный момент цианобутадиина». J. Mol. Spectrosc . 62 (2): 175–180. Bibcode : 1976JMoSp..62..175A. doi : 10.1016/0022-2852(76)90347-7.Иллюстрировано в Hollas 1996, с. 97
17. Банвелл и Маккэш 1994, стр. 63.
18. Банвелл и Маккэш 1994, стр. 40
19. Аткинс и де Паула 2006, с. 449
20. Banwell & McCash 1994, стр. 45
21. Jennings, DA; Evenson, KM; Zink, LR; Demuynck, C.; Destombes, JL; Lemoine, B; Johns, JWC (апрель 1987 г.). «Высокоразрешающая спектроскопия HF от 40 до 1100 см ⁻¹ : высокоточные вращательные константы». Журнал молекулярной спектроскопии . 122 (2): 477–480. Bibcode : 1987JMoSp.122..477J. doi : 10.1016/0022-2852(87)90021-X.pdf
22. Strandberg, MWP; Meng, CY; Ingersoll, JG (1949). "Спектр поглощения микроволн кислородом". Phys. Rev. 75 ( 10): 1524–8. Bibcode :1949PhRv...75.1524S. doi :10.1103/PhysRev.75.1524.pdf
23. Крупение, Пол Х. (1972). "Спектр молекулярного кислорода" (PDF) . Журнал физических и химических справочных данных . 1 (2): 423–534. Bibcode : 1972JPCRD...1..423K. doi : 10.1063/1.3253101.
24. Холлас 1996, стр. 101
25. Холлас 1996, стр. 102 показывает влияние H на микроволновый спектр
    ₃SiNCS .
26. Холлас 1996, стр. 103
27. Холл, Ричард Т.; Доулинг, Джером М. (1967). «Чистый вращательный спектр водяного пара». J. Chem. Phys . 47 (7): 2454–61. Bibcode : 1967JChPh..47.2454H. doi : 10.1063/1.1703330.Холл, Ричард Т.; Доулинг, Джером М. (1971). "Erratum: Pure Rotational Spectrum of Water Vapor". J. Chem. Phys . 54 (11): 4968. Bibcode :1971JChPh..54.4968H. doi : 10.1063/1.1674785 .
28. Симмонс, Джеймс У.; Андерсон, Уоллес Э.; Горди, Уолтер (1950). «Микроволновый спектр и молекулярные константы цианида водорода». Phys. Rev. 77 ( 1): 77–79. Bibcode : 1950PhRv...77...77S. doi : 10.1103/PhysRev.77.77.
29. Чанг, Рэймонд (1971). Основные принципы спектроскопии . McGraw-Hill.стр.139
30. Холлас 1996, стр. 102 дает уравнения для двухатомных молекул и симметричных волчков
31. Холлас 1996, стр. 102
32. Burkhalter, James H.; Roy S. Anderson; William V. Smith; Walter Gordy (1950). «Тонкая структура спектра поглощения микроволн кислородом». Phys. Rev. 79 ( 4): 651–5. Bibcode : 1950PhRv...79..651B. doi : 10.1103/PhysRev.79.651.
33. Холлас 1996, стр. 113, иллюстрирует спектр¹⁵
    Н
    ₂получено с использованием излучения 476,5 нм аргонового ионного лазера .
34. Cleeton, CE; Williams, NH (1934). «Электромагнитные волны длиной 1,1 см и спектр поглощения аммиака». Physical Review . 45 (4): 234–7. Bibcode : 1934PhRv...45..234C. doi : 10.1103/PhysRev.45.234.
35. Горди, В. (1948). «Микроволновая спектроскопия». Reviews of Modern Physics . 20 (4): 668–717. Bibcode : 1948RvMP...20..668G. doi : 10.1103/RevModPhys.20.668.
36. «Июнь 1971 г., Hewlett-Packard Journal» (PDF) .
37. Швендеманн, Р. Х. (1978). «Переходные эффекты в микроволновой спектроскопии». Annu. Rev. Phys. Chem . 29 : 537–558. Bibcode :1978ARPC...29..537S. doi :10.1146/annurev.pc.29.100178.002541.
38. Дикке, Р. Х.; Ромер, Р. Х. (1955). «Импульсные методы в микроволновой спектроскопии». Rev. Sci. Instrum . 26 (10): 915–928. Bibcode : 1955RScI...26..915D. doi : 10.1063/1.1715156.
39. Ekkers, J.; Flygare, WH (1976). "Импульсный микроволновый Фурье-спектрометр". Rev. Sci. Instrum . 47 (4): 448–454. Bibcode : 1976RScI...47..448E. doi : 10.1063/1.1134647.
40. Balle, TJ; Campbell, EJ; Keenan, MR; Flygare, WH (1980). «Новый метод наблюдения вращательных спектров слабых молекулярных комплексов: KrHCl». J. Chem. Phys . 72 (2): 922–932. Bibcode :1980JChPh..72..922B. doi :10.1063/1.439210.
41. Джагер, В. «Анимация спектрометра Balle-Flygare FTMW».
42. "Веб-страница исследовательской группы BH Pate, кафедра химии, Университет Вирджинии".
43. Браун, GG; Дайан, BC; Дугласс, KO; Гейер, SM; Пейт, BH (2006). «Вращательный спектр эпифторгидрина, измеренный с помощью микроволновой спектроскопии Фурье с чирпированным импульсом». J. Mol. Spectrosc . 238 (2): 200–212. Bibcode : 2006JMoSp.238..200B. doi : 10.1016/j.jms.2006.05.003.
44. Grubbs, GS; Dewberry, CT; Etchison, KC; Kerr, KE; Cooke, SA (2007). "Поиск ускоренного корректного интенсивности Фурье-преобразующего микроволнового спектрометра с источником импульсной лазерной абляции". Rev. Sci. Instrum . 78 (9): 096106–096106–3. Bibcode : 2007RScI...78i6106G. doi : 10.1063/1.2786022. PMID  17902981.
45. Wilcox, DS; Hotopp, KM; Dian, BC (2011). «Двумерная микроволновая спектроскопия с преобразованием Фурье с чирпированным импульсом». J. Phys. Chem. A. 115 ( 32): 8895–8905. Bibcode : 2011JPCA..115.8895W. doi : 10.1021/jp2043202. PMID  21728367.

Библиография

• Аткинс, П. В.; де Паула, Дж. (2006). «Молекулярная спектроскопия: Раздел: Спектры чистого вращения». Физическая химия (8-е изд.). Oxford University Press. С. 431–469. ISBN 0198700725.
• Банвелл, Колин Н.; Маккэш, Элейн М. (1994). Основы молекулярной спектроскопии (4-е изд.). McGraw-Hill. ISBN 0-07-707976-0.
• Браун, Джон М.; Каррингтон, Алан (2003). Вращательная спектроскопия двухатомной молекулы. Cambridge University Press. ISBN 0-521-53078-4.
• Холлас, М.Дж. (1996). Современная спектроскопия (3-е изд.). Wiley. ISBN 0471965227.
• Kroto, HW (2003). Молекулярная вращательная спектроскопия . Довер. ISBN 0-486-49540-X.
• МакКуорри, Дональд А. (2008). Квантовая химия. Книги по университетской науке. ISBN 978-1-891389-50-4.
• Таунс, Чарльз Х .; Шавлов, Артур Л. (1975). Микроволновая спектроскопия. Дувр. ISBN 978-0-486-61798-5.
• Ковач, Иштван (1969). Вращательная структура в спектрах двухатомных молекул . Адам Хильгер. ISBN 0852741421.
• Wollrab, James E. (1967). Вращательные спектры и молекулярная структура. Academic Press. ISBN 148319485X.

Внешние ссылки

• симулятор инфракрасных газовых спектров
• Статья в журнале Hyperphysics о вращательном спектре
• Список исследовательских групп по микроволновой спектроскопии по всему миру