Молекулярная симметрия

Симметрия молекул химических соединений

Элементы симметрии формальдегида . C ₂ — ось вращения двойного порядка. σ _v и σ _v ' — две неэквивалентные плоскости отражения.

В химии молекулярная симметрия описывает симметрию, присутствующую в молекулах , и классификацию этих молекул в соответствии с их симметрией. Молекулярная симметрия является фундаментальной концепцией в химии, поскольку ее можно использовать для предсказания или объяснения многих химических свойств молекулы , таких как наличие или отсутствие у нее дипольного момента , а также ее разрешенных спектроскопических переходов . Для этого необходимо использовать теорию групп . Это включает в себя классификацию состояний молекулы с использованием неприводимых представлений из таблицы характеров группы симметрии молекулы. Симметрия полезна при изучении молекулярных орбиталей с приложениями к методу Хюккеля , теории лигандного поля и правилам Вудворда-Хоффмана . Во многих университетских учебниках по физической химии , квантовой химии , спектроскопии и неорганической химии обсуждается симметрия. ^{[1] [2] [3] [4] [5]} Другая структура в более широком масштабе — это использование кристаллических систем для описания кристаллографической симметрии в объемных материалах.

Существует множество методов определения симметрии данной молекулы, включая рентгеновскую кристаллографию и различные формы спектроскопии . Спектроскопическая нотация основана на соображениях симметрии.

Концепции симметрии точечной группы

Элементы

Симметрия точечной группы молекулы определяется наличием или отсутствием 5 типов элементов симметрии .

• Ось симметрии : ось, вокруг которой вращение на приводит к тому, что молекула становится неотличимой от оригинала. Это также называется n -кратной осью вращения и сокращенно обозначается как C _n . Примерами являются ось C ₂ в воде и ось C ₃ в аммиаке . Молекула может иметь более одной оси симметрии; та, у которой n больше, называется главной осью и по соглашению совпадает с осью z в ​​декартовой системе координат . ${\displaystyle {\tfrac {360^{\circ }}{n}}}$
• Плоскость симметрии : плоскость отражения, через которую создается идентичная копия исходной молекулы. Ее также называют зеркальной плоскостью и сокращают до σ (сигма = греч. «s», от немецкого «Spiegel», что означает зеркало). ^[6] У воды их две: одна в плоскости самой молекулы и одна перпендикулярная ей. Плоскость симметрии , параллельная главной оси, называется вертикальной (σ _v ), а другая перпендикулярная ей — горизонтальной (σ _h ). Существует третий тип плоскости симметрии: если вертикальная плоскость симметрии дополнительно делит пополам угол между двумя осями вращения 2-го порядка, перпендикулярными главной оси, плоскость называется двугранной (σ _d ). Плоскость симметрии также можно определить по ее декартовой ориентации, например, (xz) или (yz).
• Центр симметрии или центр инверсии , сокращенно i . Молекула имеет центр симметрии, когда для любого атома в молекуле существует идентичный атом диаметрально противоположно этому центру на равном расстоянии от него. Другими словами, молекула имеет центр симметрии, когда точки (x,y,z) и (−x,−y,−z) молекулы всегда выглядят идентичными. Например, если в некоторой точке (x,y,z) находится атом кислорода, то в точке (−x,−y,−z) также должен быть атом кислорода. В самом центре инверсии может быть или не быть атом. Центр инверсии является особым случаем наличия оси вращения-отражения вокруг угла 180°, проходящей через центр. Примерами являются тетрафторид ксенона (квадратная плоская молекула), где центр инверсии находится на атоме Xe, и бензол ( C
  ₆ЧАС
  ₆), где центр инверсии находится в центре кольца.
• Ось вращения-отражения : ось, вокруг которой вращение на , за которым следует отражение в плоскости, перпендикулярной ей, оставляет молекулу неизменной. Также называется n -кратной несобственной осью вращения , сокращенно S _n . Примеры присутствуют в тетраэдрическом тетрафториде кремния с тремя осями S ₄ и в шахматной конформации этана с одной осью S ₆ . Ось S ₁ соответствует зеркальной плоскости σ , а ось S ₂ является центром инверсии i . Молекула, не имеющая оси S _n для любого значения n , является хиральной молекулой . ${\displaystyle {\tfrac {360^{\circ }}{n}}}$
• Тождественность , сокращенно E , от немецкого 'Einheit', что означает единство. ^[7] Этот элемент симметрии просто не состоит из изменений: каждая молекула имеет этот элемент симметрии, который эквивалентен собственному вращению C _1. Он должен быть включен в список элементов симметрии, чтобы они образовали математическую группу , определение которой требует включения элемента тождества. Он так называется, потому что он аналогичен умножению на единицу (единство). ^[8]

Точечные группы и их операции симметрии

Операции

XeF ₄ , с квадратной плоской геометрией, имеет 1 ось C _{4 и 4 оси} C _{2 ,} ортогональные к C ₄ . Эти пять осей плюс плоскость зеркала, перпендикулярная оси C _{4 ,} определяют группу симметрии D _4h молекулы.

Пять элементов симметрии связаны с пятью типами операций симметрии , которые оставляют геометрию молекулы неотличимой от исходной геометрии. Иногда их отличают от элементов симметрии с помощью каретки или циркумфлекса . Таким образом, Ĉ _n — это вращение молекулы вокруг оси, а Ê — операция тождества. Элемент симметрии может иметь более одной связанной с ним операции симметрии. Например, ось C ₄ квадратной молекулы тетрафторида ксенона (XeF ₄ ) связана с двумя вращениями Ĉ ₄ в противоположных направлениях (90° и 270°), вращением Ĉ ₂ (180°) и Ĉ ₁ (0° или 360°). Поскольку Ĉ ₁ эквивалентно Ê , Ŝ ₁ — σ и Ŝ ₂ — î , все операции симметрии можно классифицировать как правильные или неправильные вращения.

Для линейных молекул вращение по часовой стрелке или против часовой стрелки вокруг молекулярной оси на любой угол Φ является операцией симметрии.

Операции вращения-отражения для октаэдрической симметрии

Неправильное вращение S ₄

Группы симметрии

Группы

Операции симметрии молекулы (или другого объекта) образуют группу . В математике группа — это набор с бинарной операцией , которая удовлетворяет четырем свойствам, перечисленным ниже.

В группе симметрии элементами группы являются операции симметрии (а не элементы симметрии), а бинарная комбинация состоит из применения сначала одной операции симметрии, а затем другой. Примером может служить последовательность вращения C ₄ вокруг оси z и отражения в плоскости xy, обозначаемая σ(xy) C ₄ . По соглашению порядок операций — справа налево.

Группа симметрии подчиняется определяющим свойствам любой группы.

1. свойство закрытия :
   Для каждой пары элементов x и y в G произведение x * y также принадлежит G.
   (в символах, для любых двух элементов x , y ∈ G , x * y также принадлежит G ).
   Это означает, что группа замкнута , так что объединение двух элементов не дает новых элементов. Операции симметрии обладают этим свойством, поскольку последовательность из двух операций создаст третье состояние, неотличимое от второго и, следовательно, от первого, так что чистый эффект на молекулу все еще является операцией симметрии. Это можно проиллюстрировать с помощью таблицы. Например, с точечной группой C ₃ существует три операции симметрии: поворот на 120°, C ₃ , поворот на 240°, C ₃ ² и поворот на 360°, что эквивалентно тождеству, E .

   

   Вкладка умножения точечной группы C2v

2. Эта таблица также иллюстрирует следующие свойства
3. Ассоциативное свойство :
   Для каждого x , y и z в G оба выражения ( x * y )* z и x *( y * z ) дают один и тот же элемент в G .
   (в символах ( x * y )* z = x *( y * z ) для любых x , y и z ∈ G )
4. существование свойства идентичности :
   В G должен быть элемент (например, e ), такой что произведение любого элемента G на e не приводит к изменению элемента.
   (в символах x * e = e * x = x для каждого x ∈ G )
5. существование обратного элемента :
   Для каждого элемента x в G должен существовать элемент y в G, такой что произведение x и y является единичным элементом e .
   (в символах для каждого x ∈ G существует y ∈ G такой, что x * y = y * x = e для каждого x ∈ G )

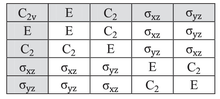
Порядок группы — это количество элементов в группе. Для групп малых порядков свойства группы можно легко проверить, рассмотрев ее таблицу состава, таблицу, строки и столбцы которой соответствуют элементам группы, а записи — их произведениям.

Точечные группы и группы перестановок-инверсий

Блок-схема определения точечной группы молекулы

Последовательное применение (или композиция ) одной или нескольких операций симметрии молекулы имеет эффект, эквивалентный эффекту некоторой отдельной операции симметрии молекулы. Например, вращение C ₂ , за которым следует отражение σ _v , рассматривается как операция симметрии σ _v ': σ _v * C ₂ = σ _v '. («Операция A , за которой следует B для образования C » записывается как BA = C ). ^[8] Более того, набор всех операций симметрии (включая эту операцию композиции) подчиняется всем свойствам группы, приведенным выше. Так что ( S , * ) — это группа, где S — набор всех операций симметрии некоторой молекулы, а * обозначает композицию (повторное применение) операций симметрии.

Эта группа называется точечной группой этой молекулы, потому что набор операций симметрии оставляет по крайней мере одну точку фиксированной (хотя для некоторых симметрий вся ось или вся плоскость остаются фиксированными). Другими словами, точечная группа — это группа, которая суммирует все операции симметрии, которые имеют все молекулы в этой категории. ^[8] Симметрия кристалла, напротив, описывается пространственной группой операций симметрии, которая включает в себя трансляции в пространстве.

Можно определить операции симметрии точечной группы для конкретной молекулы, рассмотрев геометрическую симметрию ее молекулярной модели. Однако, когда используется точечная группа для классификации молекулярных состояний, операции в ней не должны интерпретироваться таким же образом. Вместо этого операции интерпретируются как вращение и/или отражение вибронных (колебательно-электронных) координат, и эти операции коммутируют с вибронным гамильтонианом. Они являются «операциями симметрии» для этого вибронного гамильтониана. Точечная группа используется для классификации по симметрии вибронных собственных состояний жесткой молекулы. Симметричная классификация вращательных уровней, собственных состояний полного (вращение-колебание-электронный) гамильтониана, может быть достигнута с помощью использования соответствующей группы перестановок-инверсий, как введено Лонге-Хиггинсом . ^[9]

Примеры точечных групп

Назначение каждой молекуле точечной группы классифицирует молекулы по категориям со схожими свойствами симметрии. Например, PCl ₃ , POF ₃ , XeO ₃ и NH ₃ все имеют идентичные операции симметрии. ^[10] Все они могут подвергаться операции тождества E , двум различным операциям вращения C ₃ и трем различным отражениям плоскости σ _v без изменения своей идентичности, поэтому они помещаются в одну точечную группу C _3v , с порядком 6. ^[8] Аналогично, вода (H ₂ O) и сероводород (H ₂ S) также имеют идентичные операции симметрии. Они обе подвергаются операции тождества E , одному вращению C ₂ и двум отражениям σ _v без изменения своей идентичности, поэтому они обе помещаются в одну точечную группу C _2v , с порядком 4. ^[11] Эта система классификации помогает ученым более эффективно изучать молекулы, поскольку химически связанные молекулы в одной и той же точечной группе, как правило, демонстрируют схожие схемы связей, диаграммы молекулярных связей и спектроскопические свойства. ^[8] Симметрия точечной группы описывает симметрию молекулы, зафиксированной в ее равновесной конфигурации в определенном электронном состоянии. Она не допускает туннелирования между минимумами или изменения формы, которые могут возникнуть из-за эффектов центробежного искажения молекулярного вращения.

Группы общих точек

В следующей таблице перечислены многие точечные группы , применимые к молекулам, помеченные с использованием обозначения Шёнфлиса , которое распространено в химии и молекулярной спектроскопии. Описания включают общие формы молекул, которые можно объяснить с помощью модели VSEPR . В каждой строке описания и примеры не имеют более высоких симметрий, что означает, что названная точечная группа охватывает все точечные симметрии.

Представления

Набор матриц , которые умножаются друг на друга способом, имитирующим таблицу умножения элементов группы, называется представлением группы . Например, для точечной группы C _2v следующие три матрицы являются частью представления группы:

${\displaystyle \underbrace {\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{C_{2}}\times \underbrace {\begin{bmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{\sigma _{\text{v}}}=\underbrace {\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}} _{\sigma '_{\text{v}}}}$

Хотя существует бесконечное число таких представлений, неприводимые представления (или "irreps") группы — это все, что нужно, поскольку все другие представления группы можно описать как прямую сумму неприводимых представлений. Кроме того, неприводимые представления — это те матричные представления, в которых матрицы находятся в своей наиболее диагональной форме, возможной.

Операции симметрии матрицы преобразования

Таблицы символов

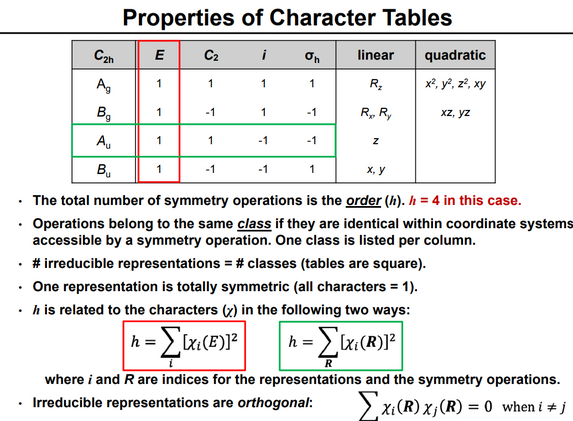
Для любой группы ее таблица характеров дает табуляцию (для классов группы) характеров (суммы диагональных элементов) матриц всех неприводимых представлений группы. Поскольку число неприводимых представлений равно числу классов, таблица характеров является квадратной.

Представления маркируются в соответствии с рядом соглашений:

• А, когда вращение вокруг главной оси симметрично
• B, когда вращение вокруг главной оси асимметрично
• E и T — дважды и трижды вырожденные представления соответственно.
• когда точечная группа имеет центр инверсии, нижний индекс g ( нем . gerade или even) сигнализирует об отсутствии изменения знака, а нижний индекс u ( ungerade или uneven) — об изменении знака относительно инверсии.
• с точечными группами C _∞v и D _∞h символы заимствованы из описания момента импульса : Σ , Π , Δ .

Таблицы также фиксируют информацию о том, как декартовы базисные векторы, вращения вокруг них и квадратичные функции от них преобразуются операциями симметрии группы, отмечая, какое неприводимое представление преобразуется таким же образом. Эти указания традиционно находятся в правой части таблиц. Эта информация полезна, поскольку химически важные орбитали (в частности, p- и d- орбитали) имеют те же симметрии, что и эти сущности.

Таблица характеров для _{точечной группы симметрии} C2v приведена ниже:

Рассмотрим пример воды (H ₂ O), которая имеет симметрию C _2v , описанную выше. Орбиталь 2 p _x кислорода имеет симметрию B ₁ , как в четвертой строке таблицы символов выше, с x в шестом столбце). Она ориентирована перпендикулярно плоскости молекулы и меняет знак с помощью операций C ₂ и σ _v '(yz), но остается неизменной с двумя другими операциями (очевидно, символ для операции тождества всегда +1). Таким образом, набор символов этой орбитали равен {1, −1, 1, −1}, что соответствует неприводимому представлению B ₁ . Аналогично, орбиталь 2 p _z имеет симметрию неприводимого представления A ₁ ( т. е .: ни одна из операций симметрии не изменяет ее), 2 p _y B ₂ и орбиталь 3 d _xy A ₂ . Эти и другие назначения отмечены в двух крайних правых столбцах таблицы.

Свойства таблицы символов

Историческая справка

Ганс Бете использовал символы операций с точечными группами в своем исследовании теории поля лигандов в 1929 году, а Юджин Вигнер использовал теорию групп для объяснения правил отбора атомной спектроскопии . ^[14] Первые таблицы символов были составлены Ласло Тиссой (1933) в связи с колебательными спектрами. Роберт Малликен был первым, кто опубликовал таблицы символов на английском языке (1933), а Э. Брайт Уилсон использовал их в 1934 году для предсказания симметрии колебательных нормальных мод . ^[15] Все описанные выше групповые операции и символы для самих кристаллографических точечных групп были впервые опубликованы Артуром Шенфлисом в 1891 году, но группы были применены другими исследователями к внешней морфологии кристаллов гораздо раньше в 19 веке. Полный набор из 32 кристаллографических точечных групп был опубликован в 1936 году Розенталем и Мерфи ^[16]

Симметрия колебательных мод

Каждый нормальный режим молекулярного колебания имеет симметрию, которая образует основу для одного неприводимого представления молекулярной группы симметрии. ^[17] Например, молекула воды имеет три нормальных режима колебания: симметричное растяжение, в котором две длины связей OH изменяются в фазе друг с другом, асимметричное растяжение, в котором они изменяются в противофазе, и изгиб, в котором изменяется угол связи. Молекулярная симметрия воды - C _2v с четырьмя неприводимыми представлениями A ₁ , A ₂ , B ₁ и B ₂ . Симметричные режимы растяжения и изгиба имеют симметрию A ₁ , в то время как асимметричный режим имеет симметрию B ₂ . Общая симметрия трех колебательных режимов, таким образом, Γ _vib = 2A ₁ + B ₂ . ^{[17] [18]}

Колебательные моды аммиака

Молекулярная симметрия аммиака (NH ₃ ) - C _3v , с операциями симметрии E, C ₃ и σ _v . ^[6] Для атомов N = 4 число колебательных мод для нелинейной молекулы составляет 3N-6 = 6 из-за относительного движения атома азота и трех атомов водорода. Все три атома водорода движутся симметрично вдоль связей NH, либо в направлении атома азота, либо от него. Этот режим известен как симметричное растяжение (v₁) и отражает симметрию в растяжении связи NH. Из трех колебательных мод этот имеет самую высокую частоту . ^[19]

Молекула аммиака ^[20]

В колебании изгиба (ν₂) атом азота остается на оси симметрии, в то время как три атома водорода движутся в разных направлениях друг от друга, что приводит к изменению углов связи. Атомы водорода движутся подобно зонтику, поэтому этот режим часто называют «режимом зонтика». ^[21]

Существует также режим асимметричного растяжения (ν₃), при котором один атом водорода приближается к атому азота, а два других водорода удаляются.

Общее число степеней свободы для каждого вида симметрии (или неприводимое представление ) может быть определено. Аммиак имеет четыре атома, и каждый атом связан с тремя векторными компонентами . Группа симметрии C _3v для NH ₃ имеет три вида симметрии A ₁ , A ₂ и E. Моды колебаний включают колебательные, вращательные и трансляционные моды.

Общее число мод = 3A ₁ + A ₂ + 4E. Всего 12 мод, поскольку каждая E соответствует 2 вырожденным модам (при одинаковой энергии).

Вращательные моды = A ₂ + E (3 моды)

Трансляционные моды = A ₁ + E

Колебательные моды = Общее количество мод - Вращательные моды - Поступательные моды = 3A ₁ + A ₂ + 4E - A ₂ - E - A ₁ - E = 2A ₁ + 2E (6 мод).

Еще примеры колебательной симметрии

• W(CO) ₆ имеет октаэдрическую геометрию. Неприводимое представление для валентного колебания CO — A _1g + E _g + T _1u . Из них только T _1u активен в ИК-диапазоне.
• B ₂ H ₆ ( диборан ) имеет молекулярную симметрию D _2h . Конечные валентные колебания BH, которые активны в ИК-спектре, — это B _2u и B _3u .

Диборан

• Fac -Mo(CO) ₃ (CH ₃ CH ₂ CN) ₃ имеет геометрию C _3v . Неприводимое представление для валентного колебания CO - A ₁ + E. Оба из них активны в ИК-диапазоне.

Симметрия молекулярных орбиталей

Каждая молекулярная орбиталь также имеет симметрию одного неприводимого представления. Например, этилен (C ₂ H ₄ ) имеет группу симметрии D _2h , а его наивысшая занятая молекулярная орбиталь ( HOMO ) является связующей pi-орбиталью, которая образует основу для его неприводимого представления B _1u . ^[22]

Молекулярное вращение и молекулярная нежесткость

Как обсуждалось выше в разделе Точечные группы и группы перестановки-инверсии, точечные группы полезны для классификации колебательных и электронных состояний жестких молекул (иногда называемых полужесткими молекулами), которые испытывают только небольшие колебания вокруг одной равновесной геометрии. Лонге-Хиггинс ввел более общий тип группы симметрии ^[9], подходящий не только для классификации колебательных и электронных состояний жестких молекул, но и для классификации их вращательных и ядерных спиновых состояний. Кроме того, такие группы могут быть использованы для классификации состояний нежестких (или флюксионных ) молекул, которые туннелируют между эквивалентными геометриями ^[23] и для учета искажающих эффектов молекулярного вращения. Эти группы известны как группы перестановки-инверсии , потому что операции симметрии в них являются энергетически возможными перестановками идентичных ядер или инверсией относительно центра масс ( операция четности ) или комбинацией этих двух. ^{[9] [24]}

Примеров молекулярной нежесткости предостаточно. Например, этан (C ₂ H ₆ ) имеет три эквивалентные ступенчатые конформации . Туннелирование между конформациями происходит при обычных температурах за счет внутреннего вращения одной метильной группы относительно другой. Это не вращение всей молекулы вокруг оси C ₃ , хотя каждая конформация имеет симметрию D _3d , как в таблице выше. Аналогично, аммиак (NH ₃ ) имеет две эквивалентные пирамидальные ( C _3v ) конформации, которые взаимопревращаются в процессе, известном как инверсия азота .

Кроме того, молекулы метана (CH ₄ ) и H ₃ ⁺ имеют высокосимметричные равновесные структуры с симметриями точечной группы T _d и D _3h соответственно; у них отсутствуют постоянные электрические дипольные моменты, но они имеют очень слабые спектры чистого вращения из-за вращательного центробежного искажения. ^{[25] [26]}

Иногда необходимо рассматривать вместе электронные состояния, имеющие различные симметрии точечной группы в равновесии. Например, в своем основном (N) электронном состоянии молекула этилена C ₂ H ₄ имеет симметрию точечной группы D _2h , тогда как в возбужденном (V) состоянии она имеет симметрию D _2d . Чтобы рассматривать эти два состояния вместе, необходимо разрешить кручение и использовать двойную группу группы перестановок-инверсий G ₁₆ . ^[27]

Смотрите также

• Четность (физика) § Молекулы
• Неприводимое представление § Приложения в теоретической физике и химии
• Правила Вудворда-Хоффмана § Диаграммы корреляции
• Тактильность § Тактильность и текучесть
• Таблица символов
• Кристаллографическая точечная группа
• Точечные группы в трех измерениях
• Симметрия двухатомных молекул
• Симметрия в квантовой механике

Ссылки

1. Квантовая химия , 3-е изд. Джон П. Лоу, Кирк Петерсон ISBN  0-12-457551-X
2. Физическая химия: молекулярный подход Дональда А. Маккуорри, Джона Д. Саймона ISBN 0-935702-99-7 
3. Химическая связь , 2-е изд. Дж. Н. Мюррелл, SFA Kettle, ISBN Дж. М. Теддера 0-471-90760-X 
4. Физическая химия , 8-е изд. PW Atkins и J. de Paula, WH Freeman, 2006 ISBN 0-7167-8759-8 , гл.12 
5. GL Miessler и DA Tarr Неорганическая химия , 2-е изд. Pearson, Prentice Hall, 1998 ISBN 0-13-841891-8 , гл.4. 
6. "Операции симметрии и таблицы символов". Университет Эксетера . 2001. Получено 29 мая 2018 г.
7. ЛЕО Ergebnisse für "einheit"
8. Пфеннинг, Брайан (2015). Принципы неорганической химии . John Wiley & Sons. ISBN 9781118859025.
9. Longuet-Higgins, HC (1963). "Группы симметрии нежестких молекул". Молекулярная физика . 6 (5): 445–460. Bibcode :1963MolPh...6..445L. doi : 10.1080/00268976300100501 .
10. Пфенниг, Брайан (30 марта 2015 г.). Принципы неорганической химии . Wiley. стр. 191. ISBN 978-1-118-85910-0.
11. Мисслер, Гэри (2004). Неорганическая химия . Пирсон. ISBN 9780321811059.
12. Мисслер, Гэри Л.; Тарр, Дональд А. (1999). "Таблицы символов (все, кроме D7h)". Неорганическая химия (2-е изд.). Prentice-Hall. стр. 621–630. ISBN 0-13-841891-8.
13. Housecroft, CE; Sharpe, AG (2008). Неорганическая химия (3-е изд.). Prentice Hall. стр. 111–112. ISBN 978-0-13-175553-6.
14. Теория групп и ее применение к квантовой механике атомных спектров , Э. П. Вигнер, Academic Press Inc. (1959)
15. Исправление двух давних ошибок в таблицах характеров симметрии точечной группы Рэндалл Б. Руберс J. Chem. Educ. 2007, 84, 1882. Аннотация
16. Розенталь, Дженни Э.; Мерфи, GM (1936). «Теория групп и колебания многоатомных молекул». Rev. Mod. Phys . 8 (4): 317–346. Bibcode : 1936RvMP....8..317R. doi : 10.1103/RevModPhys.8.317.
17. Harris, Daniel C.; Bertolucci, Michael D. (1978). "3". Симметрия и спектроскопия . Oxford University Press. стр. 138–142. ISBN 0-19-502001-4. Каждая нормальная мода колебаний будет формировать базисный набор для неприводимого представления точечной группы молекулы.
18. GL Miessler и DA Tarr Неорганическая химия , 2-е изд. Pearson, Prentice Hall, 1998 ISBN 0-13-841891-8 , стр.97-100. 
19. "Колебательные моды аммиака". www.chem.purdue.edu . Получено 2024-04-13 .
20. Гринвуд, НН; Эрншоу, А. (1997)   Химия элементов (2-е изд.), Оксфорд: Баттерворт-Хайнеманн, стр. 423   ISBN 0-7506-3365-4 
21. "Режим Umbrella - Большая химическая энциклопедия". chempedia.info . Получено 2024-04-13 .
22. Харрис, Дэниел С.; Бертолуччи, Майкл Д. (1978). "4". Симметрия и спектроскопия . Oxford University Press. стр. 278. ISBN 0-19-502001-4.
23. Bone, RGA; et al. (1991). «Переходные состояния из молекулярных групп симметрии: Анализ нежесткого ацетиленового тримера». Молекулярная физика . 72 (1): 33–73. Bibcode :1991MolPh..72...33B. doi :10.1080/00268979100100021.
24. Шнелл, М. (2010). «Понимание спектров высокого разрешения нежестких молекул с использованием теории групп». ChemPhysChem . 11 (4): 750–780. doi :10.1002/cphc.200900760.
25. Уотсон, Дж. К. Г. (1971). «Запрещенные вращательные спектры многоатомных молекул». Журнал молекулярной спектроскопии . 40 (3): 546–544. Bibcode : 1971JMoSp..40..536W. doi : 10.1016/0022-2852(71)90255-4.
26. Oldani, M.; et al. (1985). "Чистые вращательные спектры метана и метана-d4 в основном колебательном состоянии, наблюдаемые методом микроволновой Фурье-спектроскопии". Журнал молекулярной спектроскопии . 110 (1): 93–105. Bibcode : 1985JMoSp.110...93O. doi : 10.1016/0022-2852(85)90215-2.
27. Уотсон, Дж. К. Г. и др. (1996). «Теория нечетных крутильных переходов в спектре комбинационного рассеяния этилена с резонансом V−N». J Chem Phys . 105 (4): 1348. Bibcode :1996JChPh.105.1348W. doi : 10.1063/1.472001 .

Внешние ссылки

• Симметрия точечной группы @ Ньюкаслский университет
• Молекулярная симметрия @ Имперский колледж Лондона
• Таблицы симметрии молекулярных точечных групп
• Таблицы характеров для точечных групп по химии
• Молекулярная симметрия онлайн @ Открытый университет Израиля
• Интернет-курс лекций по молекулярной симметрии @ Bergische Universitaet
• ДЕКОР – Симметрия @ Кембриджский центр кристаллографических данных