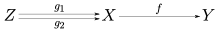
В контексте абстрактной алгебры или универсальной алгебры мономорфизм — это инъективный гомоморфизм . Мономорфизм из X в Y часто обозначается обозначением .
В более общем контексте теории категорий мономорфизм (также называемый моническим морфизмом или моно ) — это левосократимый морфизм . То есть, стрелка f : X → Y такая, что для всех объектов Z и всех морфизмов g 1 , g 2 : Z → X ,
Мономорфизмы являются категориальным обобщением инъективных функций (также называемых «функциями один к одному»); в некоторых категориях понятия совпадают, но мономорфизмы являются более общими, как в примерах ниже.
В условиях частично упорядоченных множеств пересечения идемпотентны : пересечение чего-либо с самим собой является самим собой. Мономорфизмы обобщают это свойство на произвольные категории. Морфизм является мономорфизмом, если он идемпотентен относительно пулбэков .
Категориально -двойственный мономорфизму является эпиморфизмом , то есть мономорфизм в категории C является эпиморфизмом в двойственной категории C op . Каждое сечение является мономорфизмом, а каждая ретракция является эпиморфизмом.
Левообратимые морфизмы обязательно являются моническими: если l является левым обратным для f (то есть l является морфизмом и ), то f является моническим, так как
Левообратимый морфизм называется расщепленным моно или секцией .
Однако мономорфизм не обязан быть левообратимым. Например, в категории Group всех групп и групповых гомоморфизмов среди них, если H является подгруппой G , то включение f : H → G всегда является мономорфизмом; но f имеет левообратный в категории тогда и только тогда, когда H имеет нормальное дополнение в G .
Морфизм f : X → Y является моническим тогда и только тогда, когда индуцированное отображение f ∗ : Hom( Z , X ) → Hom( Z , Y ) , определенное соотношением f ∗ ( h ) = f ∘ h для всех морфизмов h : Z → X , является инъективным для всех объектов Z .
Каждый морфизм в конкретной категории, базовая функция которой инъективна, является мономорфизмом; другими словами, если морфизмы на самом деле являются функциями между множествами, то любой морфизм, который является функцией один к одному, обязательно будет мономорфизмом в категорическом смысле. В категории множеств обратное также верно, поэтому мономорфизмы являются в точности инъективными морфизмами. Обратное также верно в большинстве естественно встречающихся категорий алгебр из-за существования свободного объекта на одном генераторе. В частности, это верно в категориях всех групп, всех колец и в любой абелевой категории .
Однако в общем случае неверно, что все мономорфизмы должны быть инъективными в других категориях; то есть существуют настройки, в которых морфизмы являются функциями между множествами, но может быть функция, которая не является инъективной и все же является мономорфизмом в категориальном смысле. Например, в категории Div делимых (абелевых) групп и групповых гомоморфизмов между ними существуют мономорфизмы, которые не являются инъективными: рассмотрим, например, фактор-отображение q : Q → Q / Z , где Q — рациональные числа по сложению, Z — целые числа (также рассматриваемые как группа по сложению), а Q / Z — соответствующая фактор-группа. Это не инъективное отображение , так как , например , каждое целое число отображается в 0. Тем не менее , это мономорфизм в этой категории. Это следует из импликации q ∘ h = 0 ⇒ h = 0 , которую мы сейчас докажем. Если h : G → Q , где G — некоторая делимая группа, и q ∘ h = 0 , то h ( x ) ∈ Z , ∀ x ∈ G . Теперь зафиксируем некоторый x ∈ G . Без потери общности можно предположить, что h ( x ) ≥ 0 (иначе вместо этого выбрать − x ). Тогда, положив n = h ( x ) + 1 , поскольку G — делимая группа, существует некоторый y ∈ G такой, что x = ny , поэтому h ( x ) = n h ( y ) . Из этого и 0 ≤ h ( x ) < h ( x ) + 1 = n следует, что
Так как h ( y ) ∈ Z , то h ( y ) = 0 , и таким образом h ( x ) = 0 = h (− x ) ∀ x ∈ G . Это говорит о том, что h = 0 , как и требовалось.
Чтобы перейти от этого следствия к тому факту, что q является мономорфизмом, предположим, что q ∘ f = q ∘ g для некоторых морфизмов f , g : G → Q , где G — некоторая делимая группа. Тогда q ∘ ( f − g ) = 0 , где ( f − g ) : x ↦ f ( x ) − g ( x ) . (Поскольку ( f − g )(0) = 0 , а ( f − g )( x + y ) = ( f − g )( x ) + ( f − g )( y ) , то отсюда следует, что ( f − g ) ∈ Hom( G , Q ) ) ). Из только что доказанного следствия следует, что q ∘ ( f − g ) = 0 ⇒ f − g = 0 ⇔ ∀ x ∈ G , f ( x ) = g ( x ) ⇔ f = g . Следовательно, q является мономорфизмом, как и утверждается.
Существуют также полезные концепции регулярного мономорфизма , экстремального мономорфизма , непосредственного мономорфизма , сильного мономорфизма и расщепляемого мономорфизма .
Сопутствующие термины мономорфизм и эпиморфизм были первоначально введены Николя Бурбаки ; Бурбаки использует мономорфизм как сокращение для инъективной функции. Ранние теоретики категорий считали, что правильным обобщением инъективности на контекст категорий было свойство отмены, приведенное выше. Хотя это не совсем верно для монических отображений, это очень близко, поэтому это вызвало мало проблем, в отличие от случая эпиморфизмов. Сондерс Маклейн попытался провести различие между тем, что он называл мономорфизмами , которые были отображениями в конкретной категории, чьи базовые отображения множеств были инъективными, и моническими отображениями , которые являются мономорфизмами в категориальном смысле этого слова. Это различие так и не вошло в общее употребление.
Другое название мономорфизма — расширение , хотя оно имеет и другие применения.