Необходимость и достаточность

В логике и математике необходимость и достаточность — это термины, используемые для описания условной или импликационной связи между двумя утверждениями . Например, в условном утверждении : «Если $P,$ то $Q$ », $Q$ необходимо для $P$ , потому что истинность Q гарантируется истинностью $P.$ (Эквивалентно, невозможно иметь $P$ без $Q$ , или ложность $Q$ гарантирует ложность $P.$ ) ^[1] Аналогично, P $достаточно$ для Q $,$ потому что $истинность$ P всегда подразумевает, что $Q$ $истинно$ , но ложность $P не всегда подразумевает$ , что $Q$ не истинно. ^[2]

В общем, необходимое условие — это одно (возможно, одно из нескольких условий), которое должно присутствовать для того, чтобы произошло другое условие, в то время как достаточное условие — это то, которое производит указанное условие. ^[3] Утверждение, что утверждение является «необходимым и достаточным» условием другого, означает, что первое утверждение истинно тогда и только тогда, когда последнее истинно. То есть, два утверждения должны быть либо одновременно истинными, либо одновременно ложными. ^[4]^[5]^[6]

В обычном английском языке (также естественном языке ) «necessary» и «sufficient» указывают на отношения между условиями или положениями дел, а не на утверждения. Например, быть мужчиной — необходимое условие для того, чтобы быть братом, но недостаточное, в то время как быть мужчиной-сиблингом — необходимое и достаточное условие для того, чтобы быть братом. Любое условное утверждение состоит по крайней мере из одного достаточного условия и по крайней мере из одного необходимого условия.

В аналитике данных необходимость и достаточность могут относиться к разным причинно-следственным логикам ^[7] , где анализ необходимых условий и качественный сравнительный анализ могут использоваться в качестве аналитических методов для изучения необходимости и достаточности условий для конкретного интересующего результата.

Определения

В условном утверждении «если S , то N » выражение, представленное S , называется антецедентом , а выражение, представленное N , называется консеквентом . Это условное утверждение может быть записано несколькими эквивалентными способами, такими как « N если S », « S только если N », « S подразумевает N », « N подразумевается S », $S \to N$ , $S \Rightarrow N$ и « N всякий раз, когда S ». ^[8]

В приведенной выше ситуации «N всякий раз, когда S», N называется необходимым условием для S. На обычном языке это эквивалентно утверждению, что если условное утверждение является истинным утверждением, то консеквент N должен быть истинным — если S должно быть истинным (см. третий столбец « таблицы истинности » непосредственно ниже). Другими словами, антецедент S не может быть истинным без того, чтобы N было истинным. Например, для того, чтобы кого-то звали Сократ , необходимо, чтобы этого кого-то звали . Аналогично, для того, чтобы люди жили, необходимо, чтобы у них был воздух. ^[9]

Можно также сказать, что S является достаточным условием для N (снова обратитесь к третьему столбцу таблицы истинности, расположенной ниже). Если условное утверждение истинно, то если S истинно, N должно быть истинным; тогда как если условное утверждение истинно и N истинно, то S может быть истинным или ложным. В общих чертах, «истинность S гарантирует истинность N ». ^[9] Например, продолжая предыдущий пример, можно сказать, что знание того, что кого-то зовут Сократ , достаточно для того, чтобы знать, что у кого-то есть Имя .

Необходимое и достаточное условие требует, чтобы оба импликации и (последняя из которых также может быть записана как ) были выполнены. Первая импликация предполагает, что S является достаточным условием для N , в то время как вторая импликация предполагает, что S является необходимым условием для N . Это выражается как « S необходимо и достаточно для N », « S тогда и только тогда, когда N », или . $S\Стрелка вправо N$ $N\Стрелка вправо S$ $S\Leftarrow N$ $S\Leftrightarrow N$

Необходимость

Утверждение, что Q необходимо для P, в разговорной речи эквивалентно выражению « P не может быть истинным, если Q не является истинным» или «если Q ложно, то P ложно». ^[9]^[1]Противоположным образом , это то же самое, что и «всякий раз, когда P истинно, то и Q истинно ».

Логическое отношение между P и Q выражается как «если P , то Q » и обозначается как « P ⇒ Q » ( P подразумевает Q ). Его также можно выразить как « P только если Q », « Q , если P », « Q всякий раз, когда P » и « Q, когда P ». Например, в математической прозе часто встречаются несколько необходимых условий, которые, взятые вместе, составляют достаточное условие (т. е. индивидуально необходимое и совместно достаточное ^[9] ), как показано в примере 5.

Пример 1

Чтобы было верно, что «Джон — холостяк», необходимо, чтобы было верно и то, что он

неженатый,
мужской,
взрослый,

поскольку утверждение «Джон — холостяк» подразумевает, что у Джона есть каждый из этих трех дополнительных предикатов .

Пример 2: Для целых чисел, больших двух, для того, чтобы быть простым, необходимо быть нечетным, поскольку два — единственное целое число, которое является и четным, и простым.

Пример 3: Рассмотрим гром, звук, вызванный молнией. Говорят, что гром необходим для молнии, так как молния никогда не случается без грома. Всякий раз, когда есть молния, есть и гром. Гром не вызывает молнию (так как молния вызывает гром), но поскольку молния всегда сопровождается громом, мы говорим, что гром необходим для молнии. (То есть, в своем формальном смысле, необходимость не подразумевает причинности.)

Пример 4: Для работы в Сенате США необходимо быть не моложе 30 лет. Если вам меньше 30 лет, то вы не можете быть сенатором. То есть, если вы сенатор, то вам должно быть не менее 30 лет.

Пример 5: В алгебре для некоторого множества S вместе с операцией для формирования группы необходимо, чтобы было ассоциативно . Также необходимо, чтобы S включало специальный элемент e такой, что для каждого x в S , имеет место случай, когда e x и x e оба равны x . Также необходимо, чтобы для каждого x в S существовал соответствующий элемент x″ , такой, что и x x″ и x″ x равны специальному элементу e . Ни одно из этих трех необходимых условий само по себе не является достаточным, но их соединение достаточно. $\звезда$ $\звезда$ $\звезда$ $\звезда$ $\звезда$ $\звезда$

Достаточность

Если P достаточно для Q , то знание того, что P истинно, является достаточным основанием для заключения, что Q истинно; однако знание того, что P ложно, не удовлетворяет минимальной потребности для заключения, что Q ложно.

Логическое отношение, как и прежде, выражается как «если P , то Q » или « P ⇒ Q ». Это также может быть выражено как « P только если Q », « P подразумевает Q » или несколькими другими вариантами. Может быть так, что несколько достаточных условий, взятые вместе, образуют единое необходимое условие (т. е. индивидуально достаточное и совместно необходимое), как показано в примере 5.

Пример 1: «Джон — король» подразумевает, что Джон — мужчина. Поэтому знание того, что Джон — король, достаточно для знания того, что он — мужчина.

Пример 2: Для того чтобы число было четным, достаточно (но не необходимо) делиться на 4, но для того, чтобы оно было четным, достаточно и необходимо делиться на 2.

Пример 3: Наличие грома является достаточным условием для возникновения молнии в том смысле, что слышание грома и однозначное распознавание его как такового позволяет сделать вывод о том, что произошла молния.

Пример 4: Если Конгресс США принимает законопроект, подписание законопроекта президентом достаточно, чтобы сделать его законом. Обратите внимание, что случай, когда президент не подписал законопроект, например, посредством использования президентского вето , не означает, что законопроект не стал законом (например, он все еще мог стать законом через отмену Конгрессом ).

Пример 5: То, что центр игральной карты должен быть отмечен одной большой пикой (♠), достаточно для того, чтобы карта была тузом. Три других достаточных условия заключаются в том, что центр карты должен быть отмечен одной бубной (♦), червой (♥) или трефой (♣). Ни одно из этих условий не является необходимым для того, чтобы карта была тузом, но их дизъюнкция необходима, поскольку ни одна карта не может быть тузом, не выполнив хотя бы (фактически, точно) одно из этих условий.

Соотношение между необходимостью и достаточностью

Условие может быть либо необходимым, либо достаточным, не будучи другим. Например, быть млекопитающим ( N ) необходимо, но недостаточно для того, чтобы быть человеком ( S ), а то, что число рационально ( S ), достаточно, но не необходимо для того, чтобы быть действительным числом ( N ) (поскольку существуют действительные числа, которые не являются рациональными). $x$ $x$

Условие может быть как необходимым, так и достаточным. Например, в настоящее время «сегодня 4 июля » является необходимым и достаточным условием для «сегодня День независимости в Соединенных Штатах » . Аналогично, необходимым и достаточным условием обратимости матрицы M является то, что M имеет ненулевой определитель .

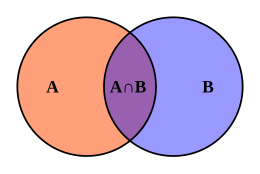
Математически говоря, необходимость и достаточность дуальны друг другу. Для любых утверждений S и N утверждение, что « N необходимо для S », эквивалентно утверждению, что « S достаточно для N ». Другой аспект этой дуальности заключается в том, что, как показано выше, конъюнкции (с использованием «и») необходимых условий могут достигать достаточности, в то время как дизъюнкции (с использованием «или») достаточных условий могут достигать необходимости. Для третьего аспекта отождествите каждый математический предикат N с множеством T ( N ) объектов, событий или утверждений, для которых N истинно ; тогда утверждение необходимости N для S эквивалентно утверждению, что T ( N ) является надмножеством T ( S ), в то время как утверждение достаточности S для N эквивалентно утверждению, что T ( S ) является подмножеством T ( N ).

Говоря психологически, необходимость и достаточность являются ключевыми аспектами классического взгляда на понятия. Согласно классической теории понятий, то, как человеческий разум представляет категорию X, порождает набор индивидуально необходимых условий, которые определяют X. Вместе эти индивидуально необходимые условия достаточны, чтобы быть X. ^[10] Это контрастирует с вероятностной теорией понятий, которая утверждает, что ни одна определяющая черта не является необходимой или достаточной, а категории напоминают структуру генеалогического древа.

Одновременная необходимость и достаточность

Сказать, что P необходимо и достаточно для Q, значит сказать две вещи:

что P необходимо для Q , , и что P достаточно для Q , . $P\Leftarrow Q$ $P\Стрелка вправо Q$
эквивалентно, это можно понимать так, что P и Q необходимы для друг друга, что также можно сформулировать так, что каждое из них достаточно для другого или подразумевает его. $P\Стрелка вправо Q\land Q\Стрелка вправо P$

Можно суммировать любой, а значит и все, из этих случаев утверждением « P тогда и только тогда, когда Q », которое обозначается как , тогда как случаи говорят нам, что идентично . $P\Leftrightarrow Q$ $P\Leftrightarrow Q$ $P\Стрелка вправо Q\land Q\Стрелка вправо P$

Например, в теории графов граф G называется двудольным, если возможно назначить каждой его вершине черный или белый цвет таким образом, чтобы каждое ребро графа G имело одну конечную точку каждого цвета. И для того, чтобы любой граф был двудольным, необходимым и достаточным условием является то, чтобы он не содержал циклов нечетной длины . Таким образом, обнаружение того, имеет ли граф какие-либо нечетные циклы, говорит нам о том, является ли он двудольным, и наоборот. Философ ^[11] мог бы охарактеризовать это положение дел следующим образом: «Хотя концепции двудольности и отсутствия нечетных циклов различаются по содержанию , они имеют одинаковое расширение . ^[12]

В математике теоремы часто формулируются в форме: « P истинно тогда и только тогда, когда Q истинно».

Потому что, как объяснялось в предыдущем разделе, необходимость одного для другого эквивалентна достаточности другого для первого, например, эквивалентно тому , что если P необходимо и достаточно для Q , то Q необходимо и достаточно для P. Мы можем записать и сказать, что утверждения « P истинно тогда и только тогда, когда Q истинно» и « Q истинно тогда и только тогда, когда P истинно» эквивалентны. $P\Leftarrow Q$ $Q\Стрелка вправо P$ $P\Leftrightarrow Q\equiv Q\Leftrightarrow P$

Смотрите также

Ссылки

^ ab "[M06] Необходимость и достаточность". philosophy.hku.hk . Получено 2019-12-02 .
^ Блох, Итан Д. (2011). Доказательства и основы: Первый курс абстрактной математики . Springer. С. 8–9. ISBN 978-1-4419-7126-5.
^ Смешение необходимого (2019-05-15). «Смешение необходимого с достаточным условием». www.txstate.edu . Получено 2019-12-02 .
^ Бетц, Фредерик (2011). Управление наукой: Методология и организация исследований . Нью-Йорк: Springer. С. 247. ISBN 978-1-4419-7487-7.
^ Manktelow, KI (1999). Рассуждение и мышление . Восточный Сассекс, Великобритания: Psychology Press. ISBN 0-86377-708-2.
^ Аснина, Эрика; Осис, Янис и Янсоне, Аснате (2013). «Формальная спецификация топологических отношений». Базы данных и информационные системы VII . 249 (Базы данных и информационные системы VII): 175. doi :10.3233/978-1-61499-161-8-175.
^ Рихтер, Николь Франциска; Хауфф, Свен (2022-08-01). «Необходимые условия в международных бизнес-исследованиях — развитие области с новой точки зрения на причинность и анализ данных» (PDF) . Журнал мирового бизнеса . 57 (5): 101310. doi : 10.1016/j.jwb.2022.101310 . ISSN 1090-9516.
^ Девлин, Кит (2004), Множества, функции и логика / Введение в абстрактную математику (3-е изд.), Chapman & Hall, стр. 22–23, ISBN 978-1-58488-449-1
^ abcd "Концепция необходимых условий и достаточных условий". www.sfu.ca . Получено 2019-12-02 .
^ «Классическая теория понятий, | Интернет-энциклопедия философии».
^ Учебник Стэнфордского университета, 2006.
^ "Значения в этом смысле часто называются интенсионалами , а обозначаемые ими вещи — экстенсионалами . Контексты, в которых имеет значение только экстенсионал, естественно, называются экстенсиональными , тогда как контексты, в которых экстенсионала недостаточно, называются интенсиональными . Математика, как правило, экстенсиональна во всем". Учебник Стэнфордского университета, 2006.

Внешние ссылки

На Викискладе есть медиафайлы по теме «Необходимость и достаточность» .

Веб-руководство по критическому мышлению: необходимые и достаточные условия
Университет Саймона Фрейзера: Концепции с примерами