Ортогональные функции

Тип функции

В математике ортогональные функции принадлежат функциональному пространству , которое представляет собой векторное пространство , имеющее билинейную форму . Когда функциональное пространство имеет интервал в качестве области определения , билинейная форма может быть интегралом произведения функций на интервале:

${\displaystyle \langle f,g\rangle =\int {\overline {f(x)}}g(x)\,dx.}$

Функции и ортогональны , когда этот интеграл равен нулю, т.е. всякий раз, когда . Как и в случае с базисом векторов в конечномерном пространстве, ортогональные функции могут образовывать бесконечный базис функционального пространства. Концептуально приведенный выше интеграл является эквивалентом векторного скалярного произведения ; два вектора являются взаимно независимыми (ортогональными), если их скалярное произведение равно нулю. ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle \langle f,\,g\rangle =0}$ ${\displaystyle f\neq g}$

Предположим – последовательность ортогональных функций ненулевых L 2 -норм . Отсюда следует, что последовательность состоит из функций L ² -нормы один, образующих ортонормированную последовательность . Чтобы иметь определенную L ² -норму, интеграл должен быть ограниченным, что ограничивает функции суммируемостью с квадратом . ${\displaystyle \{f_{0},f_{1},\ldots \}}$ ${\textstyle \left\|f_{n}\right\|_{2}={\sqrt {\langle f_{n},f_{n}\rangle }}=\left(\int f_{n}^{2}\ dx\right)^{\frac {1}{2}}}$ ${\displaystyle \left\{f_{n}/\left\|f_{n}\right\|_{2}\right\}}$

Тригонометрические функции

Несколько наборов ортогональных функций стали стандартными базами для аппроксимации функций. Например, синусоидальные функции sin nx и sin mx ортогональны на интервале, когда n и m являются положительными целыми числами. Тогда ${\displaystyle x\in (-\pi ,\pi )}$ ${\displaystyle m\neq n}$

${\displaystyle 2\sin \left(mx\right)\sin \left(nx\right)=\cos \left(\left(m-n\right)x\right)-\cos \left(\left(m+n\right)x\right),}$

и интеграл от произведения двух синусоидальных функций обращается в нуль. ^[1] Вместе с косинусными функциями эти ортогональные функции могут быть собраны в тригонометрический полином для аппроксимации заданной функции на интервале ее рядом Фурье .

Полиномы

Если начать с мономиальной последовательности на интервале и применить процесс Грама – Шмидта , то можно получить полиномы Лежандра . Другой набор ортогональных полиномов — это связанные с ними полиномы Лежандра . ${\displaystyle \left\{1,x,x^{2},\dots \right\}}$ ${\displaystyle [-1,1]}$

При изучении ортогональных полиномов используются весовые функции , которые вставляются в билинейной форме: ${\displaystyle w(x)}$

${\displaystyle \langle f,g\rangle =\int w(x)f(x)g(x)\,dx.}$

Для полиномов Лагерра весовая функция равна . ${\displaystyle (0,\infty )}$ ${\displaystyle w(x)=e^{-x}}$

И физики, и теоретики вероятности используют полиномы Эрмита от , где весовая функция равна или . ${\displaystyle (-\infty ,\infty )}$ ${\displaystyle w(x)=e^{-x^{2}}}$ ${\displaystyle w(x)=e^{-x^{2}/2}}$

Chebyshev polynomials are defined on ${\displaystyle [-1,1]}$ and use weights ${\textstyle w(x)={\frac {1}{\sqrt {1-x^{2}}}}}$ or ${\textstyle w(x)={\sqrt {1-x^{2}}}}$.

Zernike polynomials are defined on the unit disk and have orthogonality of both radial and angular parts.

Binary-valued functions

Walsh functions and Haar wavelets are examples of orthogonal functions with discrete ranges.

Rational functions

Plot of the Chebyshev rational functions of order n=0,1,2,3 and 4 between x=0.01 and 100.

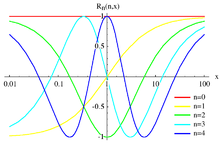
Legendre and Chebyshev polynomials provide orthogonal families for the interval [−1, 1] while occasionally orthogonal families are required on [0, ∞). In this case it is convenient to apply the Cayley transform first, to bring the argument into [−1, 1]. This procedure results in families of rational orthogonal functions called Legendre rational functions and Chebyshev rational functions.

In differential equations

Solutions of linear differential equations with boundary conditions can often be written as a weighted sum of orthogonal solution functions (a.k.a. eigenfunctions), leading to generalized Fourier series.

See also

• Eigenvalues and eigenvectors
• Hilbert space
• Karhunen–Loève theorem
• Lauricella's theorem
• Wannier function

References

1. Antoni Zygmund (1935) Trigonometrical Series, page 6, Mathematical Seminar, University of Warsaw

• George B. Arfken & Hans J. Weber (2005) Mathematical Methods for Physicists, 6th edition, chapter 10: Sturm-Liouville Theory — Orthogonal Functions, Academic Press.
• Price, Justin J. (1975). "Topics in orthogonal functions". American Mathematical Monthly. 82: 594–609. doi:10.2307/2319690.
• Giovanni Sansone (translated by Ainsley H. Diamond) (1959) Orthogonal Functions, Interscience Publishers.

External links

• Orthogonal Functions, on MathWorld.