В математике и физике вектор — это термин, который относится к величинам , которые не могут быть выражены одним числом ( скаляром ), или к элементам некоторых векторных пространств . Они должны быть выражены как величиной, так и направлением.
Исторически векторы были введены в геометрии и физике (обычно в механике ) для величин, имеющих как величину, так и направление, таких как перемещения , силы и скорости . Такие величины представлены геометрическими векторами так же, как расстояния , массы и время представлены действительными числами .
Термин вектор также используется в некоторых контекстах для кортежей , которые представляют собой конечные последовательности (чисел или других объектов) фиксированной длины.
Как геометрические векторы, так и кортежи можно складывать и масштабировать, и эти векторные операции привели к концепции векторного пространства, которое представляет собой множество, снабженное векторным сложением и скалярным умножением , которые удовлетворяют некоторым аксиомам, обобщающим основные свойства операций над указанными выше видами векторов. Векторные пространства, образованные геометрическими векторами, называются евклидовыми векторными пространствами , а векторные пространства, образованные кортежами, называются координатными векторными пространствами .
В математике рассматриваются многие векторные пространства, такие как поля расширения , полиномиальные кольца , алгебры и функциональные пространства . Термин вектор обычно не используется для элементов этих векторных пространств и обычно зарезервирован для геометрических векторов, кортежей и элементов неопределенных векторных пространств (например, при обсуждении общих свойств векторных пространств).

В математике , физике и технике евклидов вектор или просто вектор (иногда называемый геометрическим вектором [1] или пространственным вектором [2] ) — это геометрический объект, имеющий величину (или длину ) и направление . Евклидовы векторы можно складывать и масштабировать для формирования векторного пространства . Векторная величина — это векторнозначная физическая величина , включающая единицы измерения и, возможно, опору , сформулированная как направленный отрезок прямой . Вектор часто изображается графически в виде стрелки, соединяющей начальную точку A с конечной точкой B [3] и обозначается
Вектор — это то, что нужно для «переноса» точки A в точку B ; латинское слово vector означает «носитель». [4] Впервые он был использован астрономами 18 века, исследовавшими вращение планет вокруг Солнца. [5] Величина вектора — это расстояние между двумя точками, а направление относится к направлению смещения от A к B. Многие алгебраические операции над действительными числами, такие как сложение , вычитание , умножение и отрицание , имеют близкие аналоги для векторов, [6] операций, которые подчиняются знакомым алгебраическим законам коммутативности , ассоциативности и дистрибутивности . Эти операции и связанные с ними законы квалифицируют евклидовы векторы как пример более обобщенной концепции векторов, определяемых просто как элементы векторного пространства .
Векторы играют важную роль в физике : скорость и ускорение движущегося объекта, а также силы, действующие на него, можно описать с помощью векторов. [7] Многие другие физические величины можно с пользой рассматривать как векторы. Хотя большинство из них не представляют расстояния (за исключением, например, положения или смещения ), их величина и направление все равно могут быть представлены длиной и направлением стрелки. Математическое представление физического вектора зависит от системы координат , используемой для его описания. Другие вектороподобные объекты, которые описывают физические величины и преобразуются аналогичным образом при изменении системы координат, включают псевдовекторы и тензоры . [8]В естественных науках векторная величина (также известная как векторная физическая величина, физический вектор или просто вектор) — это векторная физическая величина . [9] [10] Обычно она формулируется как произведение единицы измерения и векторного числового значения ( безразмерного ), часто евклидова вектора с величиной и направлением . Например, вектор положения в физическом пространстве может быть выражен тремя декартовыми координатами с единицей СИ — метрами .
В физике и технике , особенно в механике , физический вектор может быть наделен дополнительной структурой по сравнению с геометрическим вектором. [11] Связанный вектор определяется как комбинация обычной векторной величины и точки приложения или точки действия . [9] [12] Связанные векторные величины формулируются как направленный отрезок прямой с определенной начальной точкой помимо величины и направления основного вектора. [9] [11] Например, сила на евклидовой плоскости имеет две декартовы компоненты в единицах СИ ньютонах и сопутствующий двумерный вектор положения в метрах, всего четыре числа на плоскости (и шесть в пространстве). [13] [14] [12] Более простым примером связанного вектора является вектор переноса из начальной точки в конечную точку; в этом случае связанный вектор представляет собой упорядоченную пару точек в одном и том же пространстве положений, причем все координаты имеют одинаковую размерность и единицу измерения (длину и метры). [15] [16] Скользящий вектор — это комбинация обычной векторной величины и линии приложения или линии действия , по которой векторная величина может быть перемещена (без поворотов). Свободный вектор — это векторная величина, имеющая неопределенную опору или область приложения; ее можно свободно перемещать без последствий; вектор смещения — это прототипический пример свободного вектора.
Помимо понятия единиц и поддержки, физические векторные величины могут также отличаться от евклидовых векторов с точки зрения метрики . Например, событие в пространстве-времени может быть представлено как позиционный четырехвектор с когерентной производной единицей метров: оно включает позиционный евклидов вектор и временной компонент, t ⋅ c 0 (включая скорость света ). В этом случае вместо евклидовой метрики принимается метрика Минковского .
Векторные величины являются обобщением скалярных величин и могут быть далее обобщены как тензорные величины . [16] Отдельные векторы могут быть упорядочены в последовательности во времени ( временной ряд ), например, векторы положения, дискретизирующие траекторию . Вектор может также быть результатом оценки в определенный момент непрерывной векторной функции (например, уравнения маятника ). В естественных науках термин «векторная величина» также охватывает векторные поля, определенные в двух- или трехмерной области пространства, например, скорость ветра над поверхностью Земли.
В качестве физических векторных величин допускаются также псевдовекторы и бивекторы .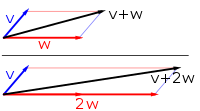
В математике и физике векторное пространство (также называемое линейным пространством) — это множество , элементы которого, часто называемые векторами , можно складывать и умножать («масштабировать») на числа, называемые скалярами . Операции сложения векторов и умножения скаляров должны удовлетворять определенным требованиям, называемым аксиомами вектора . Действительные векторные пространства и комплексные векторные пространства — это виды векторных пространств, основанные на различных видах скаляров: действительных числах и комплексных числах . Скаляры также могут быть, в более общем смысле, элементами любого поля .
Векторные пространства обобщают евклидовы векторы , которые позволяют моделировать физические величины (такие как силы и скорости ), которые имеют не только величину , но и направление . Концепция векторных пространств является фундаментальной для линейной алгебры , вместе с концепцией матриц , которая позволяет производить вычисления в векторных пространствах. Это обеспечивает краткий и синтетический способ манипулирования и изучения систем линейных уравнений .
Векторные пространства характеризуются своей размерностью , которая, грубо говоря, определяет число независимых направлений в пространстве. Это означает, что для двух векторных пространств над заданным полем и с одинаковой размерностью свойства, зависящие только от структуры векторного пространства, в точности одинаковы (технически векторные пространства изоморфны ) . Векторные пространства являются конечномерными, если их размерность является натуральным числом . В противном случае они являются бесконечномерными , а их размерность является бесконечным кардиналом . Конечномерные векторные пространства естественным образом встречаются в геометрии и смежных областях. Бесконечномерные векторные пространства встречаются во многих областях математики. Например, полиномиальные кольца являются счетно -бесконечномерными векторными пространствами, а многие функциональные пространства имеют мощность континуума в качестве размерности.
Многие векторные пространства, рассматриваемые в математике, также наделены другими структурами . Это случай алгебр , которые включают расширения полей , кольца полиномов, ассоциативные алгебры и алгебры Ли . Это также случай топологических векторных пространств , которые включают функциональные пространства, пространства скалярного произведения , нормированные пространства , гильбертовы пространства и банаховы пространства .Каждая алгебра над полем является векторным пространством, но элементы алгебры обычно не называются векторами. Однако в некоторых случаях их называют векторами , в основном по историческим причинам.
Набор кортежей из n действительных чисел имеет естественную структуру векторного пространства, определяемую покомпонентным сложением и скалярным умножением . Обычно эти кортежи называют векторами , даже в контекстах, где операции векторного пространства не применяются. В более общем смысле, когда некоторые данные могут быть естественным образом представлены векторами, их часто называют векторами, даже когда сложение и скалярное умножение векторов не являются допустимыми операциями для этих данных. [ оспаривается – обсудить ] Вот несколько примеров.
Исчисление служит основополагающим математическим инструментом в области векторов, предлагая структуру для анализа и манипулирования векторными величинами в различных научных дисциплинах, в частности, физике и инженерии . Векторнозначные функции, где выход является вектором, тщательно изучаются с помощью исчисления для получения существенной информации о движении в трехмерном пространстве. Вектор исчисления расширяет традиционные принципы исчисления на векторные поля, вводя такие операции, как градиент , дивергенция и ротор , которые находят применение в физических и инженерных контекстах. Линейные интегралы , имеющие решающее значение для вычисления работы вдоль пути в силовых полях, и поверхностные интегралы , используемые для определения величин, таких как поток , иллюстрируют практическую полезность исчисления в векторном анализе. Объемные интегралы , имеющие важное значение для вычислений, включающих скалярные или векторные поля в трехмерных областях, способствуют пониманию распределения массы , плотности заряда и скоростей потока жидкости. [ требуется ссылка ]
Векторным полем называется векторнозначная функция , которая, как правило, имеет область определения той же размерности (как многообразие ), что и ее область определения,