Дивергенция

Векторный оператор в векторном исчислении

Расхождение различных векторных полей. Расхождение векторов из точки ( x , y ) равно сумме частной производной по x компонента x и частной производной по y компонента y в этой точке: ${\displaystyle \nabla \!\cdot (\mathbf {V} (x,y))={\frac {\partial \,{V_{x}(x,y)}}{\partial {x}}}+{\frac {\partial \,{V_{y}(x,y)}}{\partial {y}}}}$

В векторном исчислении дивергенция — это векторный оператор , который действует на векторное поле , создавая скалярное поле, дающее количество источника векторного поля в каждой точке. Более технически, дивергенция представляет собой объемную плотность внешнего потока векторного поля из бесконечно малого объема вокруг заданной точки.

В качестве примера рассмотрим воздух, нагреваемый или охлаждаемый. Скорость воздуха в каждой точке определяет векторное поле. Пока воздух нагревается в некоторой области, он расширяется во всех направлениях, и, таким образом, поле скорости направлено наружу от этой области. Таким образом, дивергенция поля скорости в этой области будет иметь положительное значение. Пока воздух охлаждается и, таким образом, сжимается, дивергенция скорости имеет отрицательное значение.

Физическая интерпретация расхождения

В физических терминах дивергенция векторного поля — это степень, в которой поток векторного поля ведет себя как источник в данной точке. Это локальная мера его «исходящей» степени — степени, в которой из бесконечно малой области пространства выходит больше векторов поля, чем входит в нее. Точка, в которой поток исходит, имеет положительную дивергенцию и часто называется «источником» поля. Точка, в которой поток направлен внутрь, имеет отрицательную дивергенцию и часто называется «стоком» поля. Чем больше поток поля через малую поверхность, охватывающую данную точку, тем больше значение дивергенции в этой точке. Точка, в которой поток через охватывающую поверхность равен нулю, имеет нулевую дивергенцию.

Дивергенция векторного поля часто иллюстрируется с использованием простого примера поля скорости жидкости или газа. Движущийся газ имеет скорость , скорость и направление в каждой точке, которые можно представить вектором , поэтому скорость газа образует векторное поле . Если газ нагревается, он расширяется. Это вызовет чистое движение частиц газа наружу во всех направлениях. Любая замкнутая поверхность в газе будет заключать в себе газ, который расширяется, поэтому будет поток газа наружу через поверхность. Поэтому поле скорости будет иметь положительную дивергенцию везде. Аналогично, если газ охлаждается, он будет сжиматься. Будет больше места для частиц газа в любом объеме, поэтому внешнее давление жидкости вызовет чистый поток объема газа внутрь через любую замкнутую поверхность. Поэтому поле скорости имеет отрицательную дивергенцию везде. Напротив, в газе при постоянной температуре и давлении чистый поток газа из любой замкнутой поверхности равен нулю. Газ может двигаться, но объемная скорость газа, втекающего в любую замкнутую поверхность, должна быть равна объемной скорости вытекающего, поэтому чистый поток равен нулю. Таким образом, скорость газа имеет нулевую дивергенцию везде. Поле, которое имеет нулевую дивергенцию везде, называется соленоидальным .

Если газ нагревается только в одной точке или небольшой области, или вводится небольшая трубка, которая подает источник дополнительного газа в одну точку, газ там будет расширяться, выталкивая частицы жидкости вокруг себя наружу во всех направлениях. Это вызовет внешнее поле скорости по всему газу, центрированное на нагретой точке. Любая замкнутая поверхность, охватывающая нагретую точку, будет иметь поток частиц газа, выходящих из нее, поэтому в этой точке есть положительная дивергенция. Однако любая замкнутая поверхность, не охватывающая точку, будет иметь постоянную плотность газа внутри, поэтому столько же частиц жидкости входит в объем, сколько и выходит из него, поэтому чистый поток из объема равен нулю. Следовательно, дивергенция в любой другой точке равна нулю.

Определение

Дивергенция в точке x представляет собой предел отношения потока через поверхность S _i (красные стрелки) к объему для любой последовательности замкнутых областей V ₁ , V ₂ , V ₃ , …, охватывающих x , которая стремится к нулевому объему: ${\displaystyle \Phi }$ ${\displaystyle |V_{i}|}$
${\displaystyle \operatorname {div} \mathbf {F} =\lim _{|V_{i}|\to 0}{\frac {\Phi (S_{i})}{|V_{i}|}}}$

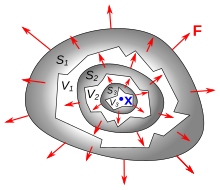
Дивергенция векторного поля F ( x ) в точке x ₀ определяется как предел отношения поверхностного интеграла F по замкнутой поверхности объема V , охватывающего x _{0 ,} к объему V , при сжатии V до нуля.

${\displaystyle \left.\operatorname {div} \mathbf {F} \right|_{\mathbf {x_{0}} }=\lim _{V\to 0}{\frac {1}{|V|}}}$ ${\displaystyle \scriptstyle S(V)}$ ${\displaystyle \mathbf {F} \cdot \mathbf {\hat {n}} \,dS}$

где | V | — объем V , S ( V ) — граница V , а — внешняя единичная нормаль к этой поверхности. Можно показать, что указанный выше предел всегда сходится к одному и тому же значению для любой последовательности объемов, которые содержат x ₀ и приближаются к нулевому объему. Результат, div F , является скалярной функцией x . ${\displaystyle \mathbf {\hat {n}} }$

Поскольку это определение не зависит от координат, оно показывает, что расхождение одинаково в любой системе координат . Однако оно нечасто используется на практике для вычисления расхождения; когда векторное поле задано в системе координат, определения координат ниже гораздо проще в использовании.

Векторное поле с нулевой дивергенцией повсюду называется соленоидальным — в этом случае любая замкнутая поверхность не имеет результирующего потока через себя.

Определение в координатах

Декартовы координаты

В трехмерных декартовых координатах дивергенция непрерывно дифференцируемого векторного поля определяется как скалярная -значная функция: ${\displaystyle \mathbf {F} =F_{x}\mathbf {i} +F_{y}\mathbf {j} +F_{z}\mathbf {k} }$

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} =\left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)\cdot (F_{x},F_{y},F_{z})={\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}.}$

Хотя результат выражен в координатах, он инвариантен относительно вращений , как предполагает физическая интерпретация. Это происходит потому, что след матрицы Якоби N -мерного векторного поля F в N -мерном пространстве инвариантен относительно любого обратимого линейного преобразования ^{[ необходимо разъяснение ]} .

Обычная нотация для дивергенции ∇ · F — это удобная мнемоника, где точка обозначает операцию, напоминающую скалярное произведение : берем компоненты оператора ∇ (см. del ), применяем их к соответствующим компонентам F и суммируем результаты. Поскольку применение оператора отличается от умножения компонентов, это считается злоупотреблением нотацией .

Цилиндрические координаты

Для вектора, выраженного в локальных цилиндрических координатах как

${\displaystyle \mathbf {F} =\mathbf {e} _{r}F_{r}+\mathbf {e} _{\theta }F_{\theta }+\mathbf {e} _{z}F_{z},}$

где e _a — единичный вектор в направлении a , дивергенция равна ^[1]

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(rF_{r}\right)+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}+{\frac {\partial F_{z}}{\partial z}}.}$

Использование локальных координат имеет решающее значение для действительности выражения. Если мы рассмотрим x как вектор положения и функции r ( x ) , θ ( x ) и z ( x ) , которые присваивают вектору соответствующую глобальную цилиндрическую координату, в общем случае , , и . В частности, если мы рассмотрим функцию тождества F ( x ) = x , мы найдем, что: ${\displaystyle r(\mathbf {F} (\mathbf {x} ))\neq F_{r}(\mathbf {x} )}$ ${\displaystyle \theta (\mathbf {F} (\mathbf {x} ))\neq F_{\theta }(\mathbf {x} )}$ ${\displaystyle z(\mathbf {F} (\mathbf {x} ))\neq F_{z}(\mathbf {x} )}$

${\displaystyle \theta (\mathbf {F} (\mathbf {x} ))=\theta \neq F_{\theta }(\mathbf {x} )=0}$.

Сферические координаты

В сферических координатах , где θ — угол с осью z , а φ — вращение вокруг оси z , а F снова записана в локальных единичных координатах, расхождение равно ^[2]

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}F_{r}\right)+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta \,F_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial F_{\varphi }}{\partial \varphi }}.}$

Тензорное поле

Пусть A — непрерывно дифференцируемое тензорное поле второго порядка, определяемое следующим образом:

${\displaystyle \mathbf {A} ={\begin{bmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{bmatrix}}}$

расхождение в декартовой системе координат является тензорным полем первого порядка ^[3] и может быть определено двумя способами: ^[4]

${\displaystyle \operatorname {div} (\mathbf {A} )={\cfrac {\partial A_{ik}}{\partial x_{k}}}~\mathbf {e} _{i}=A_{ik,k}~\mathbf {e} _{i}={\begin{bmatrix}{\dfrac {\partial A_{11}}{\partial x_{1}}}+{\dfrac {\partial A_{12}}{\partial x_{2}}}+{\dfrac {\partial A_{13}}{\partial x_{3}}}\\{\dfrac {\partial A_{21}}{\partial x_{1}}}+{\dfrac {\partial A_{22}}{\partial x_{2}}}+{\dfrac {\partial A_{23}}{\partial x_{3}}}\\{\dfrac {\partial A_{31}}{\partial x_{1}}}+{\dfrac {\partial A_{32}}{\partial x_{2}}}+{\dfrac {\partial A_{33}}{\partial x_{3}}}\end{bmatrix}}}$

и ^{[5] [6] [7]}

${\displaystyle \nabla \cdot \mathbf {A} ={\cfrac {\partial A_{ki}}{\partial x_{k}}}~\mathbf {e} _{i}=A_{ki,k}~\mathbf {e} _{i}={\begin{bmatrix}{\dfrac {\partial A_{11}}{\partial x_{1}}}+{\dfrac {\partial A_{21}}{\partial x_{2}}}+{\dfrac {\partial A_{31}}{\partial x_{3}}}\\{\dfrac {\partial A_{12}}{\partial x_{1}}}+{\dfrac {\partial A_{22}}{\partial x_{2}}}+{\dfrac {\partial A_{32}}{\partial x_{3}}}\\{\dfrac {\partial A_{13}}{\partial x_{1}}}+{\dfrac {\partial A_{23}}{\partial x_{2}}}+{\dfrac {\partial A_{33}}{\partial x_{3}}}\\\end{bmatrix}}}$

У нас есть

${\displaystyle \operatorname {div} (\mathbf {A^{T}} )=\nabla \cdot \mathbf {A} }$

Если тензор симметричен A _ij = A _ji , то . В связи с этим часто в литературе эти два определения (и символы div и ) используются взаимозаменяемо (особенно в уравнениях механики, где предполагается симметрия тензора). ${\displaystyle \operatorname {div} (\mathbf {A} )=\nabla \cdot \mathbf {A} }$ ${\displaystyle \nabla \cdot }$

Выражения в цилиндрических и сферических координатах приведены в статье del в цилиндрических и сферических координатах . ${\displaystyle \nabla \cdot \mathbf {A} }$

Общие координаты

Используя обозначения Эйнштейна, мы можем рассмотреть расхождение в общих координатах , которое мы записываем как x ¹ , …, x ⁱ , …, x ⁿ , где n — число измерений домена. Здесь верхний индекс относится к числу координат или компонента, поэтому x ² относится ко второму компоненту, а не к величине x в квадрате. Индексная переменная i используется для ссылки на произвольный компонент, такой как x ⁱ . Затем расхождение можно записать с помощью формулы Фосса- Вейля ^[8] как:

${\displaystyle \operatorname {div} (\mathbf {F} )={\frac {1}{\rho }}{\frac {\partial \left(\rho \,F^{i}\right)}{\partial x^{i}}},}$

где — локальный коэффициент элемента объема , а F ⁱ — компоненты относительно локального ненормализованного ковариантного базиса (иногда обозначаемого как ) . Обозначение Эйнштейна подразумевает суммирование по i , поскольку оно появляется как верхний, так и нижний индекс. ${\displaystyle \rho }$ ${\displaystyle \mathbf {F} =F^{i}\mathbf {e} _{i}}$ ${\displaystyle \mathbf {e} _{i}=\partial \mathbf {x} /\partial x^{i}}$

Коэффициент объема ρ является функцией положения, которая зависит от системы координат. В декартовых, цилиндрических и сферических координатах, используя те же соглашения, что и раньше, мы имеем ρ = 1 , ρ = r и ρ = r ² sin θ , соответственно. Объем также может быть выражен как , где g _ab — метрический тензор . Определитель появляется, потому что он обеспечивает соответствующее инвариантное определение объема, учитывая набор векторов. Поскольку определитель является скалярной величиной, которая не зависит от индексов, их можно опустить, записав . Абсолютное значение берется для того, чтобы обработать общий случай, когда определитель может быть отрицательным, например, в псевдоримановых пространствах. Причина для квадратного корня немного тонка: он эффективно избегает двойного счета при переходе от криволинейных к декартовым координатам и обратно. Объем (определитель) можно также понимать как якобиан преобразования из декартовых координат в криволинейные, что при n = 3 дает . ${\textstyle \rho ={\sqrt {\left|\det g_{ab}\right|}}}$ ${\textstyle \rho ={\sqrt {\left|\det g\right|}}}$ ${\textstyle \rho =\left|{\frac {\partial (x,y,z)}{\partial (x^{1},x^{2},x^{3})}}\right|}$

Некоторые соглашения предполагают, что все локальные базисные элементы должны быть нормализованы до единичной длины, как это было сделано в предыдущих разделах. Если мы запишем для нормализованного базиса и для компонентов F относительно него, то получим, что ${\displaystyle {\hat {\mathbf {e} }}_{i}}$ ${\displaystyle {\hat {F}}^{i}}$

${\displaystyle \mathbf {F} =F^{i}\mathbf {e} _{i}=F^{i}\|{\mathbf {e} _{i}}\|{\frac {\mathbf {e} _{i}}{\|\mathbf {e} _{i}\|}}=F^{i}{\sqrt {g_{ii}}}\,{\hat {\mathbf {e} }}_{i}={\hat {F}}^{i}{\hat {\mathbf {e} }}_{i},}$

используя одно из свойств метрического тензора. Расставив точки над обеими сторонами последнего равенства с контравариантным элементом , можно заключить, что . После подстановки формула становится: ${\displaystyle {\hat {\mathbf {e} }}^{i}}$ ${\textstyle F^{i}={\hat {F}}^{i}/{\sqrt {g_{ii}}}}$

${\displaystyle \operatorname {div} (\mathbf {F} )={\frac {1}{\rho }}{\frac {\partial \left({\frac {\rho }{\sqrt {g_{ii}}}}{\hat {F}}^{i}\right)}{\partial x^{i}}}={\frac {1}{\sqrt {\det g}}}{\frac {\partial \left({\sqrt {\frac {\det g}{g_{ii}}}}\,{\hat {F}}^{i}\right)}{\partial x^{i}}}.}$

Более подробное обсуждение см . в § В криволинейных координатах .

Характеристики

Следующие свойства могут быть выведены из обычных правил дифференцирования исчисления . Самое важное, что дивергенция является линейным оператором , т.е.

${\displaystyle \operatorname {div} (a\mathbf {F} +b\mathbf {G} )=a\operatorname {div} \mathbf {F} +b\operatorname {div} \mathbf {G} }$

для всех векторных полей F и G и всех действительных чисел a и b .

Существует правило произведения следующего типа: если φ — скалярная функция, а F — векторное поле, то

${\displaystyle \operatorname {div} (\varphi \mathbf {F} )=\operatorname {grad} \varphi \cdot \mathbf {F} +\varphi \operatorname {div} \mathbf {F} ,}$

или в более выразительной форме

${\displaystyle \nabla \cdot (\varphi \mathbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\varphi (\nabla \cdot \mathbf {F} ).}$

Другое правило для перекрестного произведения двух векторных полей F и G в трех измерениях включает ротор и выглядит следующим образом:

${\displaystyle \operatorname {div} (\mathbf {F} \times \mathbf {G} )=\operatorname {curl} \mathbf {F} \cdot \mathbf {G} -\mathbf {F} \cdot \operatorname {curl} \mathbf {G} ,}$

или

${\displaystyle \nabla \cdot (\mathbf {F} \times \mathbf {G} )=(\nabla \times \mathbf {F} )\cdot \mathbf {G} -\mathbf {F} \cdot (\nabla \times \mathbf {G} ).}$

Лапласиан скалярного поля — это дивергенция градиента поля :

${\displaystyle \operatorname {div} (\operatorname {grad} \varphi )=\Delta \varphi .}$

Дивергенция ротора любого векторного поля (в трех измерениях) равна нулю:

${\displaystyle \nabla \cdot (\nabla \times \mathbf {F} )=0.}$

Если векторное поле F с нулевой дивергенцией определено на шаре в R ³ , то существует некоторое векторное поле G на шаре с F = rot G . Для областей в R ³ топологически более сложных, чем эта, последнее утверждение может быть ложным (см. лемму Пуанкаре ). Степень несостоятельности утверждения, измеряемая гомологиями цепного комплекса

${\displaystyle \{{\text{scalar fields on }}U\}~{\overset {\operatorname {grad} }{\rightarrow }}~\{{\text{vector fields on }}U\}~{\overset {\operatorname {curl} }{\rightarrow }}~\{{\text{vector fields on }}U\}~{\overset {\operatorname {div} }{\rightarrow }}~\{{\text{scalar fields on }}U\}}$

служит хорошей количественной оценкой сложности базовой области U. Это начало и основные мотивы когомологий де Рама .

Теорема разложения

Можно показать, что любой стационарный поток v ( r ) , который дважды непрерывно дифференцируем в R ³ и исчезает достаточно быстро при | r | → ∞, может быть однозначно разложен на безвихревую часть E ( r ) и часть без источника B ( r ) . Более того, эти части явно определяются соответствующими плотностями источника (см. выше) и плотностями циркуляции (см. статью Curl ):

Для безвихревой части имеем

${\displaystyle \mathbf {E} =-\nabla \Phi (\mathbf {r} ),}$

с

${\displaystyle \Phi (\mathbf {r} )=\int _{\mathbb {R} ^{3}}\,d^{3}\mathbf {r} '\;{\frac {\operatorname {div} \mathbf {v} (\mathbf {r} ')}{4\pi \left|\mathbf {r} -\mathbf {r} '\right|}}.}$

Часть, свободную от источника, B , можно записать аналогичным образом: нужно только заменить скалярный потенциал Φ( r ) векторным потенциалом A ( r ) и члены −∇Φ на +∇ × A , а плотность источника div v на плотность циркуляции ∇ × v .

Эта «теорема разложения» является побочным продуктом стационарного случая электродинамики . Это частный случай более общего разложения Гельмгольца , которое работает также в измерениях больше трех.

В произвольных конечных измерениях

Дивергенция векторного поля может быть определена в любом конечном числе измерений. Если ${\displaystyle n}$

${\displaystyle \mathbf {F} =(F_{1},F_{2},\ldots F_{n}),}$

в евклидовой системе координат с координатами x ₁ , x ₂ , ..., x _n , определить

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial F_{1}}{\partial x_{1}}}+{\frac {\partial F_{2}}{\partial x_{2}}}+\cdots +{\frac {\partial F_{n}}{\partial x_{n}}}.}$

В одномерном случае F сводится к регулярной функции, а дивергенция сводится к производной.

Для любого n дивергенция является линейным оператором и удовлетворяет «правилу произведения»

${\displaystyle \nabla \cdot (\varphi \mathbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\varphi (\nabla \cdot \mathbf {F} )}$

для любой скалярной функции φ .

Отношение к внешней производной

Можно выразить дивергенцию как частный случай внешней производной , которая переводит 2-форму в 3-форму в R ³ . Определим текущую 2-форму как

${\displaystyle j=F_{1}\,dy\wedge dz+F_{2}\,dz\wedge dx+F_{3}\,dx\wedge dy.}$

Он измеряет количество «вещества», протекающего через поверхность за единицу времени в «жидкости вещества» с плотностью ρ = 1 dx ∧ dy ∧ dz, движущейся с локальной скоростью F. Его внешняя производная dj затем задается как

${\displaystyle dj=\left({\frac {\partial F_{1}}{\partial x}}+{\frac {\partial F_{2}}{\partial y}}+{\frac {\partial F_{3}}{\partial z}}\right)dx\wedge dy\wedge dz=(\nabla \cdot {\mathbf {F} })\rho }$

где — клиновое произведение . ${\displaystyle \wedge }$

Таким образом, дивергенция векторного поля F может быть выражена как:

${\displaystyle \nabla \cdot {\mathbf {F} }={\star }d{\star }{\big (}{\mathbf {F} }^{\flat }{\big )}.}$

Здесь верхний индекс ♭ — один из двух музыкальных изоморфизмов , а ⋆ — оператор звезды Ходжа . Когда дивергенция записана таким образом, оператор называется кодифференциалом . Работать с текущей 2-формой и внешней производной обычно проще, чем работать с векторным полем и дивергенцией, потому что в отличие от дивергенции внешняя производная коммутирует с изменением (криволинейной) системы координат. ${\displaystyle {\star }d{\star }}$

В криволинейных координатах

Соответствующее выражение более сложно в криволинейных координатах . Дивергенция векторного поля естественным образом распространяется на любое дифференцируемое многообразие размерности n , имеющее объемную форму (или плотность ) μ , например, риманово или лоренцево многообразие . Обобщая конструкцию двумерной формы для векторного поля на R ³ , на таком многообразии векторное поле X определяет ( n − 1) -форму j = i _X  μ, полученную сверткой X с μ . Дивергенция тогда является функцией, определяемой формулой

${\displaystyle dj=(\operatorname {div} X)\mu .}$

Расхождение можно определить через производную Ли как

${\displaystyle {\mathcal {L}}_{X}\mu =(\operatorname {div} X)\mu .}$

Это означает, что дивергенция измеряет скорость расширения единицы объема ( элемента объема ) по мере ее движения вместе с векторным полем.

На псевдоримановом многообразии дивергенция по объему может быть выражена через связность Леви-Чивиты ∇ :

${\displaystyle \operatorname {div} X=\nabla \cdot X={X^{a}}_{;a},}$

где второе выражение представляет собой свертку векторного поля, имеющего значение 1-формы ∇ X, с самим собой, а последнее выражение представляет собой традиционное координатное выражение из исчисления Риччи .

Эквивалентное выражение без использования связи:

${\displaystyle \operatorname {div} (X)={\frac {1}{\sqrt {\left|\det g\right|}}}\,\partial _{a}\left({\sqrt {\left|\det g\right|}}\,X^{a}\right),}$

где g — метрика и обозначает частную производную по координате x ^a . Квадратный корень (абсолютной величины определителя ) метрики появляется, потому что расхождение должно быть записано с правильной концепцией объема . В криволинейных координатах базисные векторы больше не являются ортонормальными; определитель кодирует правильное представление об объеме в этом случае. Он появляется дважды, здесь один раз, так что может быть преобразовано в «плоское пространство» (где координаты на самом деле ортонормальны), и еще раз, так что также преобразуется в «плоское пространство», так что, наконец, «обычная» расхождение может быть записано с «обычной» концепцией объема в плоском пространстве ( т. е. единичный объем, т. е. один, т. е. не записано). Квадратный корень появляется в знаменателе, потому что производная преобразуется противоположным образом ( контравариантно ) в вектор (который является ковариантным ). Эта идея перехода к «плоской системе координат», в которой локальные вычисления могут быть выполнены обычным способом, называется vielbein . Другой способ увидеть это — заметить, что расхождение — это замаскированный кодифференциал. То есть, расхождение соответствует выражению с дифференциалом и звездой Ходжа . Звезда Ходжа , по своей конструкции, заставляет объемную форму появляться во всех нужных местах. ${\displaystyle \partial _{a}}$ ${\displaystyle X^{a}}$ ${\displaystyle \partial _{a}}$ ${\displaystyle \star d\star }$ ${\displaystyle d}$ ${\displaystyle \star }$

Расхождение тензоров

Дивергенция может быть также обобщена на тензоры . В обозначениях Эйнштейна дивергенция контравариантного вектора F ^μ задается как

${\displaystyle \nabla \cdot \mathbf {F} =\nabla _{\mu }F^{\mu },}$

где ∇ _μ обозначает ковариантную производную . В этой общей постановке правильная формулировка дивергенции заключается в признании того, что это кодифференциал ; соответствующие свойства следуют отсюда.

Эквивалентно , некоторые авторы определяют дивергенцию смешанного тензора , используя музыкальный изоморфизм ♯ : если T является ( p , q ) -тензором ( p для контравариантного вектора и q для ковариантного), то мы определяем дивергенцию T как ( p , q − 1) -тензор

${\displaystyle (\operatorname {div} T)(Y_{1},\ldots ,Y_{q-1})={\operatorname {trace} }{\Big (}X\mapsto \sharp (\nabla T)(X,\cdot ,Y_{1},\ldots ,Y_{q-1}){\Big )};}$

то есть мы берем след по первым двум ковариантным индексам ковариантной производной. ^[a] Символ относится к музыкальному изоморфизму . ${\displaystyle \sharp }$

Смотрите также

• Завиток
• Del в цилиндрических и сферических координатах
• Теорема о дивергенции
• Градиент

Примечания

1. Выбор «первого» ковариантного индекса тензора является внутренним и зависит от порядка членов декартова произведения векторных пространств, на которых тензор задан как полилинейное отображение V × V × ... × V → R . Но столь же хорошо определенный выбор для расхождения может быть сделан с использованием других индексов. Следовательно, более естественно указать расхождение T относительно указанного индекса. Однако есть два важных особых случая , когда этот выбор по существу не имеет значения: с полностью симметричным контравариантным тензором, когда каждый выбор эквивалентен, и с полностью антисимметричным контравариантным тензором ( он же k -вектор), когда выбор влияет только на знак.

Цитаты

1. Цилиндрические координаты в Wolfram Mathworld
2. Сферические координаты в Wolfram Mathworld
3. Гуртин 1981, стр. 30.
4. "1.14 Тензорное исчисление I: Тензорные поля" (PDF) . Основы механики сплошных сред . Архивировано (PDF) из оригинала 2013-01-08.
5. Уильям М. Дин (2016). Введение в химическую инженерию механики жидкости. Cambridge University Press. стр. 133. ISBN 978-1-107-12377-9.
6. Тасос К. Папанастасиу; Георгиос К. Георгиу; Андреас Н. Александру (2000). Поток вязкой жидкости (PDF) . ЦРК Пресс. п. 66,68. ISBN 0-8493-1606-5. Архивировано (PDF) из оригинала 2020-02-20.
7. Адам Пауэлл (12 апреля 2010 г.). «Уравнения Навье-Стокса» (PDF) .
8. Гринфельд, Павел. "Формула Фосса-Вейля (ссылка на YouTube)". YouTube . Архивировано из оригинала 2021-12-11 . Получено 9 января 2018 .

Ссылки

• Брюэр, Джесс Х. (1999). "ДИВЕРГЕНЦИЯ векторного поля". musr.phas.ubc.ca . Архивировано из оригинала 2007-11-23 . Получено 2016-08-09 .
• Рудин, Уолтер (1976). Принципы математического анализа . McGraw-Hill. ISBN 0-07-054235-X.
• Эдвардс, CH (1994). Расширенное исчисление нескольких переменных . Минеола, Нью-Йорк: Довер. ISBN 0-486-68336-2.
• Гуртин, Мортон (1981). Введение в механику сплошной среды . Academic Press. ISBN 0-12-309750-9.
• Корн, Тереза ​​М.; Корн, Гранино Артур (январь 2000 г.). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора . Нью-Йорк: Dover Publications. стр. 157–160. ISBN 0-486-41147-8.

Внешние ссылки

• «Расхождение», Энциклопедия математики , EMS Press , 2001 [1994]
• Идея дивергенции векторного поля
• Академия Хана: Видеоурок «Расхождение»
• Сандерсон, Грант (21 июня 2018 г.). «Расхождение и завихрение: язык уравнений Максвелла, поток жидкости и многое другое». 3Blue1Brown . Архивировано из оригинала 2021-12-11 – через YouTube .