Частота среза

Граница частотной характеристики

Амплитудная передаточная функция полосового фильтра с нижней частотой среза 3 дБ f ₁ и верхней частотой среза 3 дБ f ₂

Диаграмма Боде (логарифмический график частотной характеристики ) любого фильтра нижних частот первого порядка с нормализованной частотой среза = 1 и полосой пропускания с единичным усилением (0 дБ). ${\displaystyle \omega }$

В физике и электротехнике частота среза , угловая частота или частота разрыва — это граница в частотной характеристике системы, при которой энергия, протекающая через систему, начинает уменьшаться ( ослабляться или отражаться), а не проходить через нее.

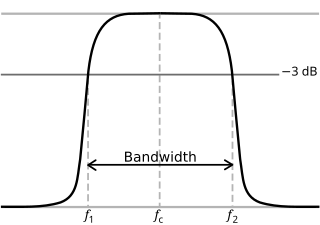
Обычно в электронных системах, таких как фильтры и каналы связи , частота среза применяется к краю в характеристике нижних частот , верхних частот , полосового фильтра или полосы задерживания — частота, характеризующая границу между полосой пропускания и полосой задерживания . Иногда ее принимают за точку в отклике фильтра, где встречаются переходная полоса и полоса пропускания, например, как определено точкой половинной мощности (частота, для которой выход схемы составляет приблизительно -3,01  дБ от номинального значения полосы пропускания). В качестве альтернативы, угловая частота полосы задерживания может быть указана как точка, где встречаются переходная полоса и полоса задерживания: частота, для которой затухание больше требуемого затухания полосы задерживания, которое, например, может составлять 30 дБ или 100 дБ.

В случае волновода или антенны граничные частоты соответствуют нижней и верхней граничным длинам волн .

Электроника

В электронике частота среза или угловая частота — это частота , выше или ниже которой выходная мощность схемы , такой как линия , усилитель или электронный фильтр, упала до заданной пропорции мощности в полосе пропускания . Чаще всего эта пропорция составляет половину мощности полосы пропускания, также называемую точкой 3  дБ , поскольку падение на 3 дБ соответствует примерно половине мощности. Как отношение напряжений это падение напряжения полосы пропускания. ^[1] Другие отношения, помимо точки 3 дБ, также могут быть важны, например, см. § Фильтры Чебышева ниже. Вдали от частоты среза в переходной полосе скорость увеличения затухания ( спад ) с логарифмом частоты асимптотически приближается к константе. Для сети первого порядка спад составляет −20 дБ на декаду (приблизительно −6 дБ на октаву .) ${\textstyle {\sqrt {1/2}}\ \approx \ 0.707}$

Пример однополюсной передаточной функции

Передаточная функция для простейшего фильтра нижних частот имеет один полюс при s = −1/ α . Величина этой функции в плоскости jω равна $${\displaystyle H(s)={\frac {1}{1+\alpha s}},}$$ $${\displaystyle \left|H(j\omega )\right|=\left|{\frac {1}{1+\alpha j\omega }}\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega ^{2}}}}.}$$

На отсечке $${\displaystyle \left|H(j\omega _{\mathrm {c} })\right|={\frac {1}{\sqrt {2}}}={\sqrt {\frac {1}{1+\alpha ^{2}\omega _{\mathrm {c} }^{2}}}}.}$$

Следовательно, частота среза определяется выражением $${\displaystyle \omega _{\mathrm {c} }={\frac {1}{\alpha }}.}$$

Где s — переменная s-плоскости , ω — угловая частота , а j — мнимая единица .

Фильтры Чебышева

Иногда другие соотношения более удобны, чем точка 3 дБ. Например, в случае фильтра Чебышева обычно определяют частоту среза как точку после последнего пика в частотной характеристике, в которой уровень упал до проектного значения пульсации полосы пропускания. Количество пульсации в этом классе фильтров может быть установлено разработчиком на любое желаемое значение, поэтому используемое соотношение может быть любым. ^[2]

Радиосвязь

В радиосвязи , связь по небесной волне представляет собой метод, при котором радиоволны передаются под углом в небо и отражаются обратно на Землю слоями заряженных частиц в ионосфере . В этом контексте термин частота отсечки относится к максимально используемой частоте , частоте, выше которой радиоволна не может отразиться от ионосферы под углом падения, необходимым для передачи между двумя указанными точками путем отражения от слоя.

Волноводы

Частота отсечки электромагнитного волновода — это самая низкая частота, при которой мода будет распространяться в нем. В волоконной оптике чаще всего рассматривают длину волны отсечки , максимальную длину волны , которая будет распространяться в оптическом волокне или волноводе . Частота отсечки находится с помощью характеристического уравнения уравнения Гельмгольца для электромагнитных волн, которое выводится из уравнения электромагнитной волны путем установки продольного волнового числа равным нулю и решения для частоты. Таким образом, любая возбуждающая частота ниже частоты отсечки будет затухать, а не распространяться. Следующий вывод предполагает отсутствие потерь на стенках. Значение c, скорость света , следует принимать за групповую скорость света в любом материале, заполняющем волновод.

Для прямоугольного волновода частота среза равна , где — номера мод для сторон прямоугольника длиной и соответственно. Для TE-мод (но не допускается), а для TM-мод . $${\displaystyle \omega _{c}=c{\sqrt {\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}}},}$$ ${\displaystyle m,n\geq 0}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle m,n\geq 0}$ ${\displaystyle m=n=0}$ ${\displaystyle m,n\geq 1}$

Частота отсечки моды TM ₀₁ (следующей по величине от доминирующей моды TE ₁₁ ) в волноводе круглого сечения (поперечно-магнитная мода без угловой зависимости и с наименьшей радиальной зависимостью) определяется выражением, где — радиус волновода, а — первый корень функции Бесселя первого рода порядка 1. $${\displaystyle \omega _{c}=c{\frac {\chi _{01}}{r}}=c{\frac {2.4048}{r}},}$$ ${\displaystyle r}$ ${\displaystyle \chi _{01}}$ ${\displaystyle J_{0}(r)}$

Частота среза доминирующей моды TE ₁₁ определяется по формуле ^[3] $${\displaystyle \omega _{c}=c{\frac {\chi _{11}}{r}}=c{\frac {1.8412}{r}}}$$

Однако частоту отсечки доминирующей моды можно снизить путем введения перегородки внутрь волновода круглого сечения. ^[4] Для одномодового оптического волокна длина волны отсечки — это длина волны, на которой нормализованная частота приблизительно равна 2,405.

Математический анализ

Отправной точкой является волновое уравнение (которое выводится из уравнений Максвелла ), которое становится уравнением Гельмгольца, если рассматривать только функции вида Подстановка и оценка производной по времени дает Функция здесь относится к любому полю (электрическому полю или магнитному полю), которое не имеет векторной составляющей в продольном направлении - "поперечному" полю. Свойством всех собственных мод электромагнитного волновода является то, что по крайней мере одно из двух полей является поперечным. Ось z определяется как проходящая вдоль оси волновода. $${\displaystyle \left(\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial {t}^{2}}}\right)\psi (\mathbf {r} ,t)=0,}$$ $${\displaystyle \psi (x,y,z,t)=\psi (x,y,z)e^{i\omega t}.}$$ $${\displaystyle \left(\nabla ^{2}+{\frac {\omega ^{2}}{c^{2}}}\right)\psi (x,y,z)=0.}$$ ${\displaystyle \psi }$

«Продольная» производная в лапласиане может быть дополнительно уменьшена путем рассмотрения только функций вида , где — продольное волновое число , в результате чего получается , где нижний индекс T указывает на двумерный поперечный лапласиан. Последний шаг зависит от геометрии волновода. Самая простая для решения геометрия — прямоугольный волновод. В этом случае остаток лапласиана можно вычислить до его характеристического уравнения, рассмотрев решения вида Таким образом, для прямоугольного волновода вычисляется лапласиан, и мы приходим к Поперечные волновые числа могут быть определены из граничных условий стоячей волны для прямоугольного сечения геометрии с размерами a и b : где n и m — два целых числа, представляющие определенную собственную моду. Выполняя окончательную замену, мы получаем , что является дисперсионным соотношением в прямоугольном волноводе. Частота отсечки — это критическая частота между распространением и затуханием, которая соответствует частоте, на которой продольное волновое число равно нулю. Это дается как Уравнения волн также справедливы ниже частоты отсечки, где продольное волновое число мнимо. В этом случае поле экспоненциально затухает вдоль оси волновода и волна, таким образом, является затухающей . $${\displaystyle \psi (x,y,z,t)=\psi (x,y)e^{i\left(\omega t-k_{z}z\right)},}$$ ${\displaystyle k_{z}}$ $${\displaystyle \left(\nabla _{T}^{2}-k_{z}^{2}+{\frac {\omega ^{2}}{c^{2}}}\right)\psi (x,y,z)=0,}$$ $${\displaystyle \psi (x,y,z,t)=\psi _{0}e^{i\left(\omega t-k_{z}z-k_{x}x-k_{y}y\right)}.}$$ $${\displaystyle {\frac {\omega ^{2}}{c^{2}}}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}$$ $${\displaystyle k_{x}={\frac {n\pi }{a}},}$$ $${\displaystyle k_{y}={\frac {m\pi }{b}},}$$ $${\displaystyle {\frac {\omega ^{2}}{c^{2}}}=\left({\frac {n\pi }{a}}\right)^{2}+\left({\frac {m\pi }{b}}\right)^{2}+k_{z}^{2},}$$ ${\displaystyle \omega _{c}}$ ${\displaystyle k_{z}}$ $${\displaystyle \omega _{c}=c{\sqrt {\left({\frac {n\pi }{a}}\right)^{2}+\left({\frac {m\pi }{b}}\right)^{2}}}}$$

Смотрите также

• Полная ширина на половине максимума
• Фильтр верхних частот
• эффект Миллера
• Пространственная частота отсечки (в оптических системах)
• Постоянная времени

Ссылки

1. Ван Валкенбург, Мэн (1974). Сетевой анализ (3-е изд.). стр. 383–384. ISBN 0-13-611095-9. Получено 22.06.2008 .
2. Матаи, Янг, Джонс Микроволновые фильтры, сети согласования импеданса и структуры связи , стр. 85-86, McGraw-Hill 1964.
3. Хантер, И.С. (2001). Теория и проектирование микроволновых фильтров. Институт инженеров-электриков. Лондон: Институт инженеров-электриков. стр. 214. ISBN 978-0-86341-253-0. OCLC  505848355.
4. Моди, Анудж Й.; Баланис, Константин А. (2016-03-01). «PEC-PMC Baffle Inside Circular Cross Section Waveguide for Reduction of Cut-Off Frequency». IEEE Microwave and Wireless Components Letters . 26 (3): 171–173. doi :10.1109/LMWC.2016.2524529. ISSN  1531-1309. S2CID  9594124.

•  В этой статье использованы материалы из общедоступного федерального стандарта 1037C. Администрация общих служб . Архивировано из оригинала 2022-01-22. (в поддержку MIL-STD-188 ).

Внешние ссылки

• Расчет центральной частоты с использованием среднего геометрического значения и сравнение со средним арифметическим решением
• Преобразование частоты среза fc и постоянной времени τ
• Математическое определение и информация о функциях Бесселя