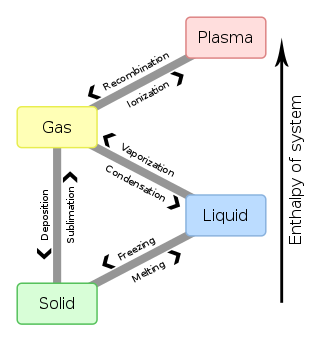
В физике , химии и других смежных областях, таких как биология, фазовый переход (или фазовое изменение ) — это физический процесс перехода из одного состояния среды в другое. Обычно этот термин используется для обозначения изменений между основными состояниями материи : твёрдым , жидким и газообразным , а в редких случаях — плазмой . Фаза термодинамической системы и состояния материи имеют однородные физические свойства . Во время фазового перехода данной среды некоторые свойства среды изменяются в результате изменения внешних условий, таких как температура или давление . Это может быть прерывистое изменение; например, жидкость может стать газом при нагревании до точки кипения , что приводит к резкому изменению объёма. Определение внешних условий, при которых происходит преобразование, определяет точку фазового перехода.

Фазовые переходы обычно относятся к тому, когда вещество переходит из одного из четырех состояний материи в другое. В точке фазового перехода для вещества, например, в точке кипения , две вовлеченные фазы — жидкость и пар — имеют одинаковую свободную энергию и, следовательно, с равной вероятностью могут существовать. Ниже точки кипения жидкость является более стабильным состоянием из двух, тогда как выше точки кипения более стабильной является газообразная форма.
Обычные переходы между твердой, жидкой и газообразной фазами одного компонента, обусловленные воздействием температуры и/или давления , указаны в следующей таблице:
Для одного компонента наиболее стабильная фаза при различных температурах и давлениях может быть показана на фазовой диаграмме . Такая диаграмма обычно изображает состояния в равновесии. Фазовый переход обычно происходит, когда давление или температура изменяются, и система переходит из одной области в другую, как вода превращается из жидкого в твердое состояние, как только температура падает ниже точки замерзания . В исключением из обычного случая, иногда возможно изменить состояние системы диабатически (в отличие от адиабатически ) таким образом, что она может пройти точку фазового перехода, не подвергаясь фазовому переходу. Результирующее состояние является метастабильным , т. е. менее стабильным, чем фаза, в которую произошел бы переход, но и не нестабильным. Это происходит , например, при перегреве и переохлаждении . Метастабильные состояния не отображаются на обычных фазовых диаграммах.
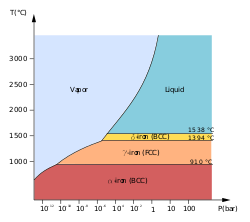
Фазовые переходы также могут происходить, когда твердое тело переходит в другую структуру без изменения своего химического состава. В элементах это известно как аллотропия , тогда как в соединениях это известно как полиморфизм . Изменение от одной кристаллической структуры к другой, от кристаллического твердого тела к аморфному твердому телу или от одной аморфной структуры к другой ( полиаморфы ) — все это примеры фазовых переходов из твердого тела в твердое тело.
Мартенситное превращение происходит как одно из многих фазовых превращений в углеродистой стали и выступает в качестве модели для сдвиговых фазовых превращений . Переходы порядок-беспорядок, такие как в альфа- титановых алюминидах . Как и в случае с состояниями вещества, существует также метастабильное равновесное фазовое превращение для структурных фазовых переходов. Метастабильный полиморф, который быстро образуется из-за более низкой поверхностной энергии, преобразуется в равновесную фазу при достаточном тепловом входе для преодоления энергетического барьера.

Фазовые переходы также могут описывать изменение между различными видами магнитного упорядочения . Наиболее известным является переход между ферромагнитной и парамагнитной фазами магнитных материалов, который происходит в так называемой точке Кюри . Другим примером является переход между по-разному упорядоченными, соразмерными или несоразмерными магнитными структурами, такими как в антимониде церия . Упрощенная, но очень полезная модель магнитных фазовых переходов предоставляется моделью Изинга
.JPG/440px-Binary_phase_diagram_of_NiTI_(phase_and_temperature).JPG)
Фазовые переходы, включающие растворы и смеси, более сложны, чем переходы, включающие одно соединение. В то время как химически чистые соединения демонстрируют единую температуру плавления между твердой и жидкой фазами, смеси могут либо иметь единую температуру плавления, известную как конгруэнтное плавление , либо иметь разные температуры ликвидуса и солидуса, что приводит к температурному интервалу, в котором твердое и жидкое состояния сосуществуют в равновесии. Это часто имеет место в твердых растворах , где два компонента являются изоструктурными.
Существует также ряд фазовых переходов, включающих три фазы: эвтектическое превращение, при котором двухкомпонентная однофазная жидкость охлаждается и превращается в две твердые фазы. Тот же процесс, но начинающийся с твердого тела вместо жидкости, называется эвтектоидным превращением. Перитектическое превращение, при котором двухкомпонентное однофазное твердое тело нагревается и превращается в твердую фазу и жидкую фазу. Перитектоидная реакция является перитектоидной реакцией, за исключением того, что в ней участвуют только твердые фазы. Монотектическая реакция состоит из изменения от жидкости к комбинации твердого тела и второй жидкости, где две жидкости демонстрируют разрыв смешиваемости . [1]
Разделение на несколько фаз может происходить посредством спинодального распада , при котором одна фаза охлаждается и разделяется на два различных состава.
Могут возникать неравновесные смеси, например, при пересыщении .

Другие фазовые изменения включают в себя:
Фазовые переходы происходят, когда термодинамическая свободная энергия системы неаналитична для некоторого выбора термодинамических переменных (ср. фазы ). Это состояние обычно возникает из-за взаимодействия большого числа частиц в системе и не проявляется в системах, которые являются малыми. Фазовые переходы могут происходить для нетермодинамических систем, где температура не является параметром. Примеры включают: квантовые фазовые переходы , динамические фазовые переходы и топологические (структурные) фазовые переходы. В этих типах систем другие параметры занимают место температуры. Например, вероятность связи заменяет температуру для перколяционных сетей.
Пауль Эренфест классифицировал фазовые переходы на основе поведения термодинамической свободной энергии как функции других термодинамических переменных. [5] Согласно этой схеме, фазовые переходы были помечены наименьшей производной свободной энергии, которая является разрывной при переходе. Фазовые переходы первого рода демонстрируют разрыв в первой производной свободной энергии по отношению к некоторой термодинамической переменной. [6] Различные переходы твердое тело/жидкость/газ классифицируются как переходы первого рода, поскольку они включают разрывное изменение плотности, которая является (обратной) первой производной свободной энергии по отношению к давлению. Фазовые переходы второго рода непрерывны по первой производной (параметр порядка, который является первой производной свободной энергии по отношению к внешнему полю, непрерывен через переход), но демонстрируют разрыв во второй производной свободной энергии. [6] К ним относятся ферромагнитный фазовый переход в таких материалах, как железо, где намагниченность , которая является первой производной свободной энергии по отношению к напряженности приложенного магнитного поля, непрерывно увеличивается от нуля по мере понижения температуры ниже температуры Кюри . Магнитная восприимчивость , вторая производная свободной энергии по полю, изменяется скачкообразно. Согласно схеме классификации Эренфеста, в принципе могут быть фазовые переходы третьего, четвертого и более высокого порядка. Например, фазовый переход Гросса–Виттена–Вадии в квантовой хромодинамике двумерной решетки является фазовым переходом третьего рода. [7] [8] Точки Кюри многих ферромагнетиков также являются переходом третьего рода, как показано их удельной теплотой, имеющей внезапное изменение наклона. [9] [10]
На практике обычно наблюдаются только фазовые переходы первого и второго рода. Фазовый переход второго рода некоторое время был спорным, так как, по-видимому, для точного соприкосновения требуются два листа свободной энергии Гиббса, что настолько маловероятно, что никогда не происходит на практике. Корнелис Гортер ответил на критику, указав, что поверхность свободной энергии Гиббса может иметь два листа с одной стороны, но только один лист с другой стороны, создавая раздвоенный вид. [11] ( [9] стр. 146--150)
Классификация Эренфеста неявно допускает непрерывные фазовые превращения, при которых характер связи материала изменяется, но нет разрыва в любой производной свободной энергии. Пример этого происходит на сверхкритических границах жидкость–газ .
Первым примером фазового перехода, который не вписывался в классификацию Эренфеста, было точное решение модели Изинга , открытое в 1944 году Ларсом Онзагером . Точная удельная теплота отличалась от более ранних приближений среднего поля , которые предсказывали, что она имеет простой разрыв при критической температуре. Вместо этого точная удельная теплота имела логарифмическую расходимость при критической температуре. [12] В последующие десятилетия классификация Эренфеста была заменена упрощенной схемой классификации, которая способна включать такие переходы.
В современной схеме классификации фазовые переходы делятся на две широкие категории, названные аналогично классам Эренфеста: [5]
Фазовые переходы первого рода — это переходы, в которых задействована скрытая теплота . Во время такого перехода система либо поглощает, либо выделяет фиксированное (и обычно большое) количество энергии на объем. Во время этого процесса температура системы будет оставаться постоянной по мере добавления тепла: система находится в «смешанно-фазовом режиме», в котором некоторые части системы завершили переход, а другие — нет. [13] [14]
Известными примерами являются таяние льда или кипение воды (вода не превращается мгновенно в пар , а образует турбулентную смесь жидкой воды и пузырьков пара). Йозеф Имри и Майкл Вортис показали, что замороженный беспорядок может расширить переход первого рода. То есть, превращение завершается в конечном диапазоне температур, но такие явления, как переохлаждение и перегрев, сохраняются, и гистерезис наблюдается при термическом циклировании. [15] [16] [17]
Фазовые переходы второго рода также называются«непрерывными фазовыми переходами». Они характеризуются расходящейся восприимчивостью, бесконечнойдлиной корреляцииистепеннымзатуханием корреляций вблизикритичности. Примерами фазовых переходов второго рода являютсяферромагнитныйпереход, сверхпроводящий переход (длясверхпроводника I типафазовый переход является переходом второго рода при нулевом внешнем поле, а длясверхпроводника II типафазовый переход является переходом второго рода как для переходов нормальное состояние–смешанное состояние, так и для переходов смешанное состояние–сверхпроводящее состояние) и сверхтекучийпереход. В отличие от вязкости, тепловое расширение и теплоемкость аморфных материалов показывают относительно внезапное изменение при температуре стеклования[18], что позволяет точно определять с помощьюизмерений дифференциальной сканирующей калориметрииЛев Ландаудалфеноменологическую теориюфазовых переходов второго рода.
Помимо изолированных, простых фазовых переходов, существуют линии перехода, а также мультикритические точки при изменении внешних параметров, таких как магнитное поле или состав.
Несколько переходов известны как фазовые переходы бесконечного порядка . Они непрерывны, но не нарушают симметрии. Самый известный пример — переход Костерлица–Таулесса в двумерной модели XY . Многие квантовые фазовые переходы , например, в двумерных электронных газах , принадлежат к этому классу.
Переход жидкость -стекло наблюдается во многих полимерах и других жидкостях, которые могут быть переохлаждены намного ниже точки плавления кристаллической фазы. Это нетипично в нескольких отношениях. Это не переход между термодинамическими основными состояниями: широко распространено мнение, что истинное основное состояние всегда кристаллическое. Стекло является закаленным состоянием беспорядка, и его энтропия, плотность и т. д. зависят от термической истории. Поэтому переход стекла является в первую очередь динамическим явлением: при охлаждении жидкости внутренние степени свободы последовательно выходят из равновесия. Некоторые теоретические методы предсказывают базовый фазовый переход в гипотетическом пределе бесконечно длинных времен релаксации. [19] [20] Никакие прямые экспериментальные доказательства не подтверждают существование этих переходов.
Переход первого рода с расширенным беспорядком происходит в конечном диапазоне температур, где доля низкотемпературной равновесной фазы растет от нуля до единицы (100%) по мере понижения температуры. Это непрерывное изменение сосуществующих фракций с температурой открыло интересные возможности. При охлаждении некоторые жидкости стеклообразуются в стекло, а не переходят в равновесную кристаллическую фазу. Это происходит, если скорость охлаждения превышает критическую скорость охлаждения, и объясняется тем, что молекулярные движения становятся настолько медленными, что молекулы не могут перестроиться в кристаллические положения. [21] Это замедление происходит ниже температуры стеклования T g , которая может зависеть от приложенного давления. [18] [22] Если переход застывания первого рода происходит в диапазоне температур, и T g попадает в этот диапазон, то существует интересная возможность того, что переход останавливается, когда он частичный и неполный. Распространение этих идей на магнитные переходы первого рода, останавливаемые при низких температурах, привело к наблюдению неполных магнитных переходов с сосуществованием двух магнитных фаз вплоть до самой низкой температуры. Впервые сообщено в случае перехода ферромагнетика в антиферромагнитный [23], такое постоянное сосуществование фаз теперь сообщается в различных магнитных переходах первого рода. К ним относятся манганитовые материалы с колоссальным магнитосопротивлением, [24] [25] магнитокалорические материалы, [26] материалы с магнитной памятью формы, [27] и другие материалы. [28] Интересной особенностью этих наблюдений T g , попадающих в температурный диапазон, в котором происходит переход, является то, что магнитный переход первого рода находится под влиянием магнитного поля, так же как структурный переход находится под влиянием давления. Относительная легкость, с которой можно контролировать магнитные поля, в отличие от давления, повышает вероятность того, что можно изучить взаимодействие между T g и T c исчерпывающим образом. Фазовое сосуществование в магнитных переходах первого рода затем позволит разрешить нерешенные вопросы в понимании стекол.
В любой системе, содержащей жидкую и газообразную фазы, существует особое сочетание давления и температуры, известное как критическая точка , в которой переход между жидкостью и газом становится переходом второго рода. Вблизи критической точки жидкость достаточно горячая и сжатая, так что различие между жидкой и газообразной фазами практически отсутствует. Это связано с явлением критической опалесценции , молочного вида жидкости из-за флуктуаций плотности на всех возможных длинах волн (включая длины волн видимого света).
Фазовые переходы часто включают процесс нарушения симметрии . Например, охлаждение жидкости в кристаллическое твердое тело нарушает непрерывную трансляционную симметрию : каждая точка в жидкости имеет те же свойства, но каждая точка в кристалле не имеет тех же свойств (если только точки не выбраны из узлов решетки кристаллической решетки). Как правило, высокотемпературная фаза содержит больше симметрий, чем низкотемпературная фаза из-за спонтанного нарушения симметрии , за исключением некоторых случайных симметрий (например, образование тяжелых виртуальных частиц , которое происходит только при низких температурах). [29]
Параметр порядка является мерой степени порядка на границах в системе фазового перехода; он обычно находится в диапазоне от нуля в одной фазе (обычно выше критической точки) до ненулевого значения в другой. [30] В критической точке восприимчивость параметра порядка обычно расходится.
Примером параметра порядка является чистая намагниченность в ферромагнитной системе, претерпевающей фазовый переход. Для переходов жидкость/газ параметром порядка является разность плотностей.
С теоретической точки зрения параметры порядка возникают из-за нарушения симметрии. Когда это происходит, необходимо ввести одну или несколько дополнительных переменных для описания состояния системы. Например, в ферромагнитной фазе необходимо указать чистую намагниченность , направление которой было выбрано спонтанно, когда система остыла ниже точки Кюри . Однако следует отметить, что параметры порядка также могут быть определены для переходов, не нарушающих симметрию. [ необходима цитата ]
Некоторые фазовые переходы, такие как сверхпроводящий и ферромагнитный, могут иметь параметры порядка для более чем одной степени свободы. В таких фазах параметр порядка может принимать форму комплексного числа, вектора или даже тензора, величина которого стремится к нулю при фазовом переходе. [ необходима цитата ]
Существуют также дуальные описания фазовых переходов в терминах параметров беспорядка. Они указывают на наличие линейных возбуждений, таких как вихревые или дефектные линии.
Фазовые переходы, нарушающие симметрию, играют важную роль в космологии . По мере расширения и охлаждения Вселенной вакуум претерпел ряд фазовых переходов, нарушающих симметрию. Например, электрослабый переход нарушил симметрию SU(2)×U(1) электрослабого поля в симметрию U(1) современного электромагнитного поля . Этот переход важен для объяснения асимметрии между количеством материи и антиматерии в современной Вселенной, согласно теории электрослабого бариогенезиса .
Прогрессивные фазовые переходы в расширяющейся Вселенной участвуют в развитии порядка во Вселенной, как показано в работах Эрика Чейссона [31] и Дэвида Лайзера . [32]
См. также теории относительного порядка и порядок и беспорядок .
Непрерывные фазовые переходы изучать легче, чем переходы первого рода, из-за отсутствия скрытой теплоты , и было обнаружено, что они обладают многими интересными свойствами. Явления, связанные с непрерывными фазовыми переходами, называются критическими явлениями из-за их связи с критическими точками.
Непрерывные фазовые переходы можно охарактеризовать параметрами, известными как критические показатели . Наиболее важным из них, возможно, является показатель, описывающий расхождение длины тепловой корреляции при приближении к переходу. Например, давайте рассмотрим поведение теплоемкости вблизи такого перехода. Мы изменяем температуру T системы, сохраняя все остальные термодинамические переменные фиксированными, и обнаруживаем, что переход происходит при некоторой критической температуре T c . Когда T близка к T c , теплоемкость C обычно имеет степенное поведение:
Теплоемкость аморфных материалов имеет такое поведение вблизи температуры стеклования, где универсальный критический показатель α = 0,59 [33]. Аналогичное поведение, но с показателем ν вместо α , применимо к длине корреляции.
Показатель ν положителен. Это отличается от α . Его фактическое значение зависит от типа рассматриваемого нами фазового перехода.
Критические показатели не обязательно одинаковы выше и ниже критической температуры. Когда непрерывная симметрия явно разбивается на дискретную симметрию нерелевантными (в смысле ренормгруппы) анизотропиями, то некоторые показатели (например , показатель восприимчивости) не идентичны. [34]
Для −1 < α < 0 теплоемкость имеет «излом» при температуре перехода. Это поведение жидкого гелия при лямбда-переходе из нормального состояния в сверхтекучее , для которого эксперименты показали α = −0,013 ± 0,003. По крайней мере один эксперимент был проведен в условиях невесомости на орбитальном спутнике, чтобы минимизировать разницу давлений в образце. [35] Это экспериментальное значение α согласуется с теоретическими предсказаниями, основанными на вариационной теории возмущений . [36]
При 0 < α < 1 теплоемкость расходится при температуре перехода (хотя, поскольку α < 1, энтальпия остается конечной). Примером такого поведения является 3D ферромагнитный фазовый переход. В трехмерной модели Изинга для одноосных магнетиков детальные теоретические исследования дали показатель степени α ≈ +0,110.
Некоторые модельные системы не подчиняются степенному закону поведения. Например, теория среднего поля предсказывает конечный разрыв теплоемкости при температуре перехода, а двумерная модель Изинга имеет логарифмическую расходимость. Однако эти системы являются предельными случаями и исключением из правила. Реальные фазовые переходы демонстрируют степенной закон поведения.
Несколько других критических показателей, β , γ , δ , ν , и η , определены, исследуя поведение степенного закона измеримой физической величины вблизи фазового перехода. Показатели связаны соотношениями масштабирования, такими как
Можно показать, что существуют только два независимых показателя степени, например, ν и η .
Примечательным фактом является то, что фазовые переходы, возникающие в различных системах, часто обладают одним и тем же набором критических показателей. Это явление известно как универсальность . Например, было обнаружено, что критические показатели в критической точке жидкость–газ не зависят от химического состава жидкости.
Что еще более впечатляюще, но понятно из вышесказанного, они точно соответствуют критическим показателям ферромагнитного фазового перехода в одноосных магнитах. Говорят, что такие системы находятся в одном классе универсальности. Универсальность — это предсказание теории ренормгруппы фазовых переходов, которая утверждает, что термодинамические свойства системы вблизи фазового перехода зависят только от небольшого числа характеристик, таких как размерность и симметрия, и нечувствительны к основным микроскопическим свойствам системы. Опять же, расхождение длины корреляции является существенным моментом.
Существуют также и другие критические явления; например, помимо статических функций существует также критическая динамика . Как следствие, при фазовом переходе можно наблюдать критическое замедление или ускорение . С предыдущим явлением связано также явление усиленных флуктуаций перед фазовым переходом, как следствие более низкой степени устойчивости начальной фазы системы. Большие статические классы универсальности непрерывного фазового перехода распадаются на меньшие динамические классы универсальности. В дополнение к критическим показателям существуют также универсальные соотношения для определенных статических или динамических функций магнитных полей и температурных разностей от критического значения. [ необходима цитата ]
Фазовые переходы играют много важных ролей в биологических системах. Примерами являются образование липидного бислоя , переход катушка-глобула в процессе сворачивания белка и плавления ДНК , жидкокристаллические переходы в процессе конденсации ДНК и кооперативное связывание лиганда с ДНК и белками с характером фазового перехода. [37]
В биологических мембранах фазовые переходы гель-жидкость-кристалл играют решающую роль в физиологическом функционировании биомембран. В гелевой фазе из-за низкой текучести жирно-ацильных цепей мембранных липидов мембранные белки имеют ограниченное движение и, таким образом, сдерживаются в выполнении своей физиологической роли. Растения критически зависят от фотосинтеза хлоропластных тилакоидных мембран , которые подвергаются воздействию низких температур окружающей среды. Тилакоидные мембраны сохраняют врожденную текучесть даже при относительно низких температурах из-за высокой степени жирно-ацильного беспорядка, допускаемого их высоким содержанием линоленовой кислоты , 18-углеродной цепи с 3-двойными связями. [38] Температура фазового перехода гель-жидкость биологических мембран может быть определена многими методами, включая калориметрию, флуоресценцию, спин-метку электронного парамагнитного резонанса и ЯМР путем регистрации измерений соответствующего параметра при ряде температур образца. Также был предложен простой метод его определения по интенсивностям линий ЯМР 13-C. [39]
Было высказано предположение, что некоторые биологические системы могут находиться вблизи критических точек. Примерами служат нейронные сети в сетчатке саламандры [40] , стаи птиц [41], сети экспрессии генов у дрозофилы [42] и сворачивание белков. [43] Однако неясно, могут ли альтернативные причины объяснить некоторые явления, подтверждающие аргументы в пользу критичности. [44] Также было высказано предположение, что биологические организмы обладают двумя ключевыми свойствами фазовых переходов: изменением макроскопического поведения и согласованностью системы в критической точке. [45] Фазовые переходы являются важной чертой двигательного поведения в биологических системах. [46] Спонтанные переходы походки [47] , а также вызванные усталостью отключения двигательных задач [48] демонстрируют типичное критическое поведение как указание на внезапное качественное изменение ранее стабильного двигательного поведенческого паттерна.
Характерной чертой фазовых переходов второго порядка является появление фракталов в некоторых свойствах без масштаба . Давно известно, что белковые глобулы формируются при взаимодействии с водой. Существует 20 аминокислот, которые образуют боковые группы на пептидных цепях белка, варьирующихся от гидрофильных до гидрофобных, заставляя первые располагаться вблизи поверхности глобулы, в то время как последние располагаются ближе к центру глобулы. Двадцать фракталов были обнаружены в связанных с растворителем областях поверхности > 5000 сегментов белка. [49] Существование этих фракталов доказывает, что белки функционируют вблизи критических точек фазовых переходов второго порядка.
В группах организмов, находящихся в состоянии стресса (при приближении к критическим переходам), корреляции имеют тенденцию к увеличению, в то же время, как и флуктуации. Этот эффект подтверждается многими экспериментами и наблюдениями за группами людей, мышей, деревьев и травянистых растений. [50]
Фазовые переходы, как предполагалось, происходят в социальных системах, рассматриваемых как динамические системы. Гипотеза, предложенная в 1990-х и 2000-х годах в контексте мира и вооруженного конфликта , заключается в том, что когда конфликт, который является ненасильственным, переходит в фазу вооруженного конфликта, это фазовый переход от латентной к явной фазе в динамической системе. [51] : 49
Для изучения различных эффектов применяются различные методы. Вот некоторые примеры:
{{cite book}}: CS1 maint: multiple names: authors list (link)![]() Медиа, связанные с изменениями фаз на Wikimedia Commons
Медиа, связанные с изменениями фаз на Wikimedia Commons