Деформация плит под нагрузкой
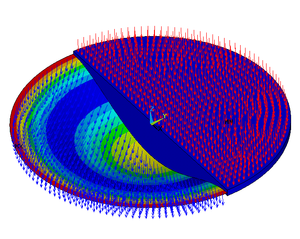
Изгиб круглой пластины, зажатой по краям, под действием поперечного давления. Левая половина пластины демонстрирует деформированную форму, а правая половина — недеформированную. Этот расчет был выполнен с помощью Ansys . Изгиб пластин , или изгиб пластины , — это прогиб пластины перпендикулярно плоскости пластины под действием внешних сил и моментов . Величину отклонения можно определить путем решения дифференциальных уравнений соответствующей теории пластин . По этим прогибам можно рассчитать напряжения в пластине. Когда напряжения известны, можно использовать теории разрушения, чтобы определить, выйдет ли пластина из строя при заданной нагрузке.
Изгиб пластин Кирхгофа-Лява. Силы и моменты на плоской пластине. Определения Для тонкой прямоугольной пластины толщиной , модуля Юнга и коэффициента Пуассона мы можем определить параметры через прогиб пластины . ЧАС {\displaystyle H} Э {\displaystyle E} ν {\displaystyle \nu } ш {\displaystyle ш}
Жесткость на изгиб определяется выражением
Д "=" Э ЧАС 3 12 ( 1 − ν 2 ) {\displaystyle D={\frac {EH^{3}}{12\left(1-\nu ^{2}\right)}}} Моменты Изгибающие моменты на единицу длины определяются выражением
М Икс "=" − Д ( ∂ 2 ш ∂ Икс 2 + ν ∂ 2 ш ∂ й 2 ) {\displaystyle M_{x}=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\frac {\partial ^{2}w} {\partial y^{2}}}\right)} М й "=" − Д ( ν ∂ 2 ш ∂ Икс 2 + ∂ 2 ш ∂ й 2 ) {\displaystyle M_{y}=-D\left(\nu {\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w} {\partial y^{2}}}\right)} Крутящий момент на единицу длины определяется выражением
М Икс й "=" − Д ( 1 − ν ) ∂ 2 ш ∂ Икс ∂ й {\displaystyle M_{xy}=-D\left(1-\nu \right){\frac {\partial ^{2}w}{\partial x\partial y}}} Силы Поперечные силы на единицу длины определяются выражением
вопрос Икс "=" − Д ∂ ∂ Икс ( ∂ 2 ш ∂ Икс 2 + ∂ 2 ш ∂ й 2 ) {\displaystyle Q_{x}=-D{\frac {\partial }{\partial x}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{ \frac {\partial ^{2}w}{\partial y^{2}}}\right)} вопрос й "=" − Д ∂ ∂ й ( ∂ 2 ш ∂ Икс 2 + ∂ 2 ш ∂ й 2 ) {\displaystyle Q_{y}=-D{\frac {\partial }{\partial y}}\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{ \frac {\partial ^{2}w}{\partial y^{2}}}\right)} Стрессы Изгибающие напряжения определяются выражением
σ Икс "=" − 12 Д я ЧАС 3 ( ∂ 2 ш ∂ Икс 2 + ν ∂ 2 ш ∂ й 2 ) {\displaystyle \sigma _{x}=-{\frac {12Dz}{H^{3}}}\left({\frac {\partial ^{2}w}{\partial x^{2}}} +\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\right)} σ й "=" − 12 Д я ЧАС 3 ( ν ∂ 2 ш ∂ Икс 2 + ∂ 2 ш ∂ й 2 ) {\displaystyle \sigma _{y}=-{\frac {12Dz}{H^{3}}}\left(\nu {\frac {\partial ^{2}w}{\partial x^{2} }}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right)} Напряжение сдвига определяется выражением
τ Икс й "=" − 12 Д я ЧАС 3 ( 1 − ν ) ∂ 2 ш ∂ Икс ∂ й {\displaystyle \tau _{xy}=- {\frac {12Dz}{H^{3}}}\left(1-\nu \right){\frac {\partial ^{2}w}{\partial х\частичный у}}} Штаммы Деформации изгиба для теории малого прогиба определяются выражением
ϵ Икс "=" ∂ ты ∂ Икс "=" − я ∂ 2 ш ∂ Икс 2 {\displaystyle \epsilon _{x}={\frac {\partial u}{\partial x}} = -z {\frac {\partial ^{2}w}{\partial x^{2}}}} ϵ й "=" ∂ в ∂ й "=" − я ∂ 2 ш ∂ й 2 {\displaystyle \epsilon _{y}={\frac {\partial v}{\partial y}} = -z {\frac {\partial ^{2}w}{\partial y^{2}}}} Сдвиговая деформация для теории малого прогиба определяется выражением
γ Икс й "=" ∂ ты ∂ й + ∂ в ∂ Икс "=" − 2 я ∂ 2 ш ∂ Икс ∂ й {\displaystyle \gamma _{xy}={\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}=-2z{\frac {\partial ^{2}w}{\partial x\partial y}}} В теории пластин с большим отклонением мы рассматриваем учет мембранных деформаций.
ϵ x = ∂ u ∂ x + 1 2 ( ∂ w ∂ x ) 2 {\displaystyle \epsilon _{x}={\frac {\partial u}{\partial x}}+{\frac {1}{2}}\left({\frac {\partial w}{\partial x}}\right)^{2}} ϵ y = ∂ v ∂ y + 1 2 ( ∂ w ∂ y ) 2 {\displaystyle \epsilon _{y}={\frac {\partial v}{\partial y}}+{\frac {1}{2}}\left({\frac {\partial w}{\partial y}}\right)^{2}} γ x y = ∂ u ∂ y + ∂ v ∂ x + ∂ w ∂ x ∂ w ∂ y {\displaystyle \gamma _{xy}={\frac {\partial u}{\partial y}}+{\frac {\partial v}{\partial x}}+{\frac {\partial w}{\partial x}}{\frac {\partial w}{\partial y}}} Прогибы Отклонения определяются выражением
u = − z ∂ w ∂ x {\displaystyle u=-z{\frac {\partial w}{\partial x}}} v = − z ∂ w ∂ y {\displaystyle v=-z{\frac {\partial w}{\partial y}}} Вывод В теории пластин Кирхгофа – Лява для пластин основными уравнениями являются [1]
N α β , α = 0 {\displaystyle N_{\alpha \beta ,\alpha }=0} и
M α β , α β − q = 0 {\displaystyle M_{\alpha \beta ,\alpha \beta }-q=0} В развернутом виде,
∂ N 11 ∂ x 1 + ∂ N 21 ∂ x 2 = 0 ; ∂ N 12 ∂ x 1 + ∂ N 22 ∂ x 2 = 0 {\displaystyle {\cfrac {\partial N_{11}}{\partial x_{1}}}+{\cfrac {\partial N_{21}}{\partial x_{2}}}=0~;~~{\cfrac {\partial N_{12}}{\partial x_{1}}}+{\cfrac {\partial N_{22}}{\partial x_{2}}}=0} и
∂ 2 M 11 ∂ x 1 2 + 2 ∂ 2 M 12 ∂ x 1 ∂ x 2 + ∂ 2 M 22 ∂ x 2 2 = q {\displaystyle {\cfrac {\partial ^{2}M_{11}}{\partial x_{1}^{2}}}+2{\cfrac {\partial ^{2}M_{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}M_{22}}{\partial x_{2}^{2}}}=q} где – приложенная поперечная нагрузка на единицу площади, толщина пластины – , напряжения – , а q ( x ) {\displaystyle q(x)} H = 2 h {\displaystyle H=2h} σ i j {\displaystyle \sigma _{ij}}
N α β := ∫ − h h σ α β d x 3 ; M α β := ∫ − h h x 3 σ α β d x 3 . {\displaystyle N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}~.} Величина имеет единицы силы на единицу длины. Величина имеет единицы момента на единицу длины. N {\displaystyle N} M {\displaystyle M}
Для изотропных однородных пластин с модулем Юнга и коэффициентом Пуассона эти уравнения сводятся к [2] E {\displaystyle E} ν {\displaystyle \nu }
∇ 2 ∇ 2 w = − q D ; D := 2 h 3 E 3 ( 1 − ν 2 ) = H 3 E 12 ( 1 − ν 2 ) {\displaystyle \nabla ^{2}\nabla ^{2}w=-{\cfrac {q}{D}}~;~~D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}={\cfrac {H^{3}E}{12(1-\nu ^{2})}}} где – прогиб средней поверхности пластины. w ( x 1 , x 2 ) {\displaystyle w(x_{1},x_{2})}
Малый прогиб тонких прямоугольных пластин. Это определяется уравнением пластины Жермена - Лагранжа .
∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = q D {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}} Это уравнение было впервые выведено Лагранжем в декабре 1811 года при исправлении работы Жермена, положившей начало теории.
Большой прогиб тонких прямоугольных пластин. Это определяется уравнениями пластины Фёппля – фон Кармана.
∂ 4 F ∂ x 4 + 2 ∂ 4 F ∂ x 2 ∂ y 2 + ∂ 4 F ∂ y 4 = E [ ( ∂ 2 w ∂ x ∂ y ) 2 − ∂ 2 w ∂ x 2 ∂ 2 w ∂ y 2 ] {\displaystyle {\cfrac {\partial ^{4}F}{\partial x^{4}}}+2{\cfrac {\partial ^{4}F}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}F}{\partial y^{4}}}=E\left[\left({\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\cfrac {\partial ^{2}w}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}\right]} ∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = q D + H D ( ∂ 2 F ∂ y 2 ∂ 2 w ∂ x 2 + ∂ 2 F ∂ x 2 ∂ 2 w ∂ y 2 − 2 ∂ 2 F ∂ x ∂ y ∂ 2 w ∂ x ∂ y ) {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}+{\cfrac {H}{D}}\left({\cfrac {\partial ^{2}F}{\partial y^{2}}}{\cfrac {\partial ^{2}w}{\partial x^{2}}}+{\cfrac {\partial ^{2}F}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}-2{\cfrac {\partial ^{2}F}{\partial x\partial y}}{\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)} где - функция напряжения. F {\displaystyle F}
Круглые тарелки Кирхгофа-Лява Изгиб круглых пластин можно изучить, решив основное уравнение с соответствующими граничными условиями. Эти решения были впервые найдены Пуассоном в 1829 году. Для таких задач удобны цилиндрические координаты. Вот расстояние точки от средней плоскости пластины. z {\displaystyle z}
Основное уравнение в бескоординатной форме имеет вид
∇ 2 ∇ 2 w = − q D . {\displaystyle \nabla ^{2}\nabla ^{2}w=-{\frac {q}{D}}\,.} В цилиндрических координатах ( r , θ , z ) {\displaystyle (r,\theta ,z)}
∇ 2 w ≡ 1 r ∂ ∂ r ( r ∂ w ∂ r ) + 1 r 2 ∂ 2 w ∂ θ 2 + ∂ 2 w ∂ z 2 . {\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}w}{\partial \theta ^{2}}}+{\frac {\partial ^{2}w}{\partial z^{2}}}\,.} Для симметрично нагруженных круглых пластин , и имеем w = w ( r ) {\displaystyle w=w(r)}
∇ 2 w ≡ 1 r d d r ( r d w d r ) . {\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\,.} Следовательно, основное уравнение имеет вид
1 r d d r [ r d d r { 1 r d d r ( r d w d r ) } ] = − q D . {\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.} Если и постоянны, прямое интегрирование основного уравнения дает нам q {\displaystyle q} D {\displaystyle D}
w ( r ) = − q r 4 64 D + C 1 ln r + C 2 r 2 2 + C 3 r 2 4 ( 2 ln r − 1 ) + C 4 {\displaystyle w(r)=-{\frac {qr^{4}}{64D}}+C_{1}\ln r+{\cfrac {C_{2}r^{2}}{2}}+{\cfrac {C_{3}r^{2}}{4}}(2\ln r-1)+C_{4}} где константы. Наклон поверхности отклонения равен C i {\displaystyle C_{i}}
ϕ ( r ) = d w d r = − q r 3 16 D + C 1 r + C 2 r + C 3 r ln r . {\displaystyle \phi (r)={\cfrac {dw}{dr}}=-{\frac {qr^{3}}{16D}}+{\frac {C_{1}}{r}}+C_{2}r+C_{3}r\ln r\,.} Для круглой пластины требование конечности прогиба и наклона прогиба при означает, что . Однако оно не обязательно должно быть равно 0, так как предел существует при приближении справа. r = 0 {\displaystyle r=0} C 1 = 0 {\displaystyle C_{1}=0} C 3 {\displaystyle C_{3}} r ln r {\displaystyle r\ln r\,} r = 0 {\displaystyle r=0}
Зажатые края Для круглой пластины с зажатыми краями имеем и на краю пластины (радиус ). Используя эти граничные условия, мы получаем w ( a ) = 0 {\displaystyle w(a)=0} ϕ ( a ) = 0 {\displaystyle \phi (a)=0} a {\displaystyle a}
w ( r ) = − q 64 D ( a 2 − r 2 ) 2 and ϕ ( r ) = q r 16 D ( a 2 − r 2 ) . {\displaystyle w(r)=-{\frac {q}{64D}}(a^{2}-r^{2})^{2}\quad {\text{and}}\quad \phi (r)={\frac {qr}{16D}}(a^{2}-r^{2})\,.} Плоскостные перемещения пластины равны
u r ( r ) = − z ϕ ( r ) and u θ ( r ) = 0 . {\displaystyle u_{r}(r)=-z\phi (r)\quad {\text{and}}\quad u_{\theta }(r)=0\,.} Плоские деформации в пластине равны
ε r r = d u r d r = − q z 16 D ( a 2 − 3 r 2 ) , ε θ θ = u r r = − q z 16 D ( a 2 − r 2 ) , ε r θ = 0 . {\displaystyle \varepsilon _{rr}={\cfrac {du_{r}}{dr}}=-{\frac {qz}{16D}}(a^{2}-3r^{2})~,~~\varepsilon _{\theta \theta }={\frac {u_{r}}{r}}=-{\frac {qz}{16D}}(a^{2}-r^{2})~,~~\varepsilon _{r\theta }=0\,.} Плоские напряжения в пластине равны
σ r r = E 1 − ν 2 [ ε r r + ν ε θ θ ] ; σ θ θ = E 1 − ν 2 [ ε θ θ + ν ε r r ] ; σ r θ = 0 . {\displaystyle \sigma _{rr}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{rr}+\nu \varepsilon _{\theta \theta }\right]~;~~\sigma _{\theta \theta }={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{\theta \theta }+\nu \varepsilon _{rr}\right]~;~~\sigma _{r\theta }=0\,.} Для пластины толщиной , жесткость на изгиб равна и имеем 2 h {\displaystyle 2h} D = 2 E h 3 / [ 3 ( 1 − ν 2 ) ] {\displaystyle D=2Eh^{3}/[3(1-\nu ^{2})]}
σ r r = − 3 q z 32 h 3 [ ( 1 + ν ) a 2 − ( 3 + ν ) r 2 ] σ θ θ = − 3 q z 32 h 3 [ ( 1 + ν ) a 2 − ( 1 + 3 ν ) r 2 ] σ r θ = 0 . {\displaystyle {\begin{aligned}\sigma _{rr}&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]\\\sigma _{\theta \theta }&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]\\\sigma _{r\theta }&=0\,.\end{aligned}}} Равнодействующие момента (изгибающие моменты) равны
M r r = − q 16 [ ( 1 + ν ) a 2 − ( 3 + ν ) r 2 ] ; M θ θ = − q 16 [ ( 1 + ν ) a 2 − ( 1 + 3 ν ) r 2 ] ; M r θ = 0 . {\displaystyle M_{rr}=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]~;~~M_{\theta \theta }=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]~;~~M_{r\theta }=0\,.} Максимальное радиальное напряжение составляет и : z = h {\displaystyle z=h} r = a {\displaystyle r=a}
σ r r | z = h , r = a = 3 q a 2 16 h 2 = 3 q a 2 4 H 2 {\displaystyle \left.\sigma _{rr}\right|_{z=h,r=a}={\frac {3qa^{2}}{16h^{2}}}={\frac {3qa^{2}}{4H^{2}}}} где . Изгибающие моменты на границе и в центре пластины равны H := 2 h {\displaystyle H:=2h}
M r r | r = a = q a 2 8 , M θ θ | r = a = ν q a 2 8 , M r r | r = 0 = M θ θ | r = 0 = − ( 1 + ν ) q a 2 16 . {\displaystyle \left.M_{rr}\right|_{r=a}={\frac {qa^{2}}{8}}~,~~\left.M_{\theta \theta }\right|_{r=a}={\frac {\nu qa^{2}}{8}}~,~~\left.M_{rr}\right|_{r=0}=\left.M_{\theta \theta }\right|_{r=0}=-{\frac {(1+\nu )qa^{2}}{16}}\,.} Прямоугольные пластинки Кирхгофа-Лява Изгиб прямоугольной пластины под действием силы, распределенной на единицу площади. q {\displaystyle q} Для прямоугольных пластин Навье в 1820 году предложил простой метод определения смещения и напряжения, когда пластина просто опирается. Идея заключалась в том, чтобы выразить приложенную нагрузку через компоненты Фурье, найти решение для синусоидальной нагрузки (одна компонента Фурье), а затем наложить компоненты Фурье, чтобы получить решение для произвольной нагрузки.
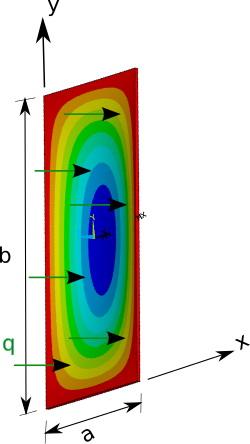
Синусоидальная нагрузка Предположим, что нагрузка имеет вид
q ( x , y ) = q 0 sin π x a sin π y b . {\displaystyle q(x,y)=q_{0}\sin {\frac {\pi x}{a}}\sin {\frac {\pi y}{b}}\,.} Здесь – амплитуда, – ширина пластины в –направлении, – ширина пластинки в –направлении. q 0 {\displaystyle q_{0}} a {\displaystyle a} x {\displaystyle x} b {\displaystyle b} y {\displaystyle y}
Так как пластина просто оперта, то перемещение по краям пластины равно нулю, изгибающий момент равен нулю при и , и равен нулю при и . w ( x , y ) {\displaystyle w(x,y)} M x x {\displaystyle M_{xx}} x = 0 {\displaystyle x=0} x = a {\displaystyle x=a} M y y {\displaystyle M_{yy}} y = 0 {\displaystyle y=0} y = b {\displaystyle y=b}
Если мы применим эти граничные условия и решим уравнение пластины, мы получим решение
w ( x , y ) = q 0 π 4 D ( 1 a 2 + 1 b 2 ) − 2 sin π x a sin π y b . {\displaystyle w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)^{-2}\,\sin {\frac {\pi x}{a}}\sin {\frac {\pi y}{b}}\,.} Где D – изгибная жесткость
D = E t 3 12 ( 1 − ν 2 ) {\displaystyle D={\frac {Et^{3}}{12(1-\nu ^{2})}}} Аналогично жесткости на изгиб EI. [3] Зная смещение, мы можем рассчитать напряжения и деформации в пластине.
Для более общей загрузки формы
q ( x , y ) = q 0 sin m π x a sin n π y b {\displaystyle q(x,y)=q_{0}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} где и являются целыми числами, мы получаем решение m {\displaystyle m} n {\displaystyle n}
(1) w ( x , y ) = q 0 π 4 D ( m 2 a 2 + n 2 b 2 ) − 2 sin m π x a sin n π y b . {\displaystyle {\text{(1)}}\qquad w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{-2}\,\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,.} Решение Навье Уравнение двойного тригонометрического ряда Определим общую нагрузку следующего вида q ( x , y ) {\displaystyle q(x,y)}
q ( x , y ) = ∑ m = 1 ∞ ∑ n = 1 ∞ a m n sin m π x a sin n π y b {\displaystyle q(x,y)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }a_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} где – коэффициент Фурье, определяемый формулой a m n {\displaystyle a_{mn}}
a m n = 4 a b ∫ 0 b ∫ 0 a q ( x , y ) sin m π x a sin n π y b d x d y {\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{b}\int _{0}^{a}q(x,y)\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y} Таким образом, классическое уравнение прямоугольной пластины для малых прогибов принимает вид:
∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = 1 D ∑ m = 1 ∞ ∑ n = 1 ∞ a m n sin m π x a sin n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {1}{D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }a_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} Просто опертая пластина с общей нагрузкой Мы предполагаем решение следующего вида w ( x , y ) {\displaystyle w(x,y)}
w ( x , y ) = ∑ m = 1 ∞ ∑ n = 1 ∞ w m n sin m π x a sin n π y b {\displaystyle w(x,y)=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} Частные дифференциалы этой функции имеют вид
∂ 4 w ∂ x 4 = ∑ m = 1 ∞ ∑ n = 1 ∞ ( m π a ) 4 w m n sin m π x a sin n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} ∂ 4 w ∂ x 2 ∂ y 2 = ∑ m = 1 ∞ ∑ n = 1 ∞ ( m π a ) 2 ( n π b ) 2 w m n sin m π x a sin n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{2}\left({\frac {n\pi }{b}}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} ∂ 4 w ∂ y 4 = ∑ m = 1 ∞ ∑ n = 1 ∞ ( n π b ) 4 w m n sin m π x a sin n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial y^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {n\pi }{b}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} Подставив эти выражения в уравнение пластины, получим
∑ m = 1 ∞ ∑ n = 1 ∞ ( ( m π a ) 2 + ( n π b ) 2 ) 2 w m n sin m π x a sin n π y b = ∑ m = 1 ∞ ∑ n = 1 ∞ a m n D sin m π x a sin n π y b {\displaystyle \sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left(\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\cfrac {a_{mn}}{D}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} Приравнивая два выражения, имеем
( ( m π a ) 2 + ( n π b ) 2 ) 2 w m n = a m n D {\displaystyle \left(\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}\right)^{2}w_{mn}={\cfrac {a_{mn}}{D}}} который можно переставить, чтобы дать
w m n = 1 π 4 D a m n ( m 2 a 2 + n 2 b 2 ) 2 {\displaystyle w_{mn}={\frac {1}{\pi ^{4}D}}{\frac {a_{mn}}{\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}} Прогиб свободно опертой пластины (углового происхождения) под действием общей нагрузки определяется выражением
w ( x , y ) = 1 π 4 D ∑ m = 1 ∞ ∑ n = 1 ∞ a m n ( m 2 a 2 + n 2 b 2 ) 2 sin m π x a sin n π y b {\displaystyle w(x,y)={\frac {1}{\pi ^{4}D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {a_{mn}}{\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} Просто опирающаяся пластина с равномерно распределенной нагрузкой Для равномерно распределенной нагрузки имеем
q ( x , y ) = q 0 {\displaystyle q(x,y)=q_{0}} Таким образом, соответствующий коэффициент Фурье определяется выражением
a m n = 4 a b ∫ 0 a ∫ 0 b q 0 sin m π x a sin n π y b d x d y {\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{a}\int _{0}^{b}q_{0}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y} Вычисляя двойной интеграл, имеем
a m n = 4 q 0 π 2 m n ( 1 − cos m π ) ( 1 − cos n π ) {\displaystyle a_{mn}={\frac {4q_{0}}{\pi ^{2}mn}}(1-\cos m\pi )(1-\cos n\pi )} или, альтернативно, в кусочном формате, мы имеем
a m n = { 16 q 0 π 2 m n m and n odd 0 m or n even {\displaystyle a_{mn}={\begin{cases}{\cfrac {16q_{0}}{\pi ^{2}mn}}&m~{\text{and}}~n~{\text{odd}}\\0&m~{\text{or}}~n~{\text{even}}\end{cases}}} Прогиб свободно опертой пластины (углового происхождения) при равномерно распределенной нагрузке определяется выражением
w ( x , y ) = 16 q 0 π 6 D ∑ m = 1 , 3 , 5 , . . . ∞ ∑ n = 1 , 3 , 5 , . . . ∞ 1 m n ( m 2 a 2 + n 2 b 2 ) 2 sin m π x a sin n π y b {\displaystyle w(x,y)={\frac {16q_{0}}{\pi ^{6}D}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {1}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} Изгибающие моменты на единицу длины пластины определяются выражением
M x = 16 q 0 π 4 ∑ m = 1 , 3 , 5 , . . . ∞ ∑ n = 1 , 3 , 5 , . . . ∞ m 2 a 2 + ν n 2 b 2 m n ( m 2 a 2 + n 2 b 2 ) 2 sin m π x a sin n π y b {\displaystyle M_{x}={\frac {16q_{0}}{\pi ^{4}}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {{\frac {m^{2}}{a^{2}}}+\nu {\frac {n^{2}}{b^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} M y = 16 q 0 π 4 ∑ m = 1 , 3 , 5 , . . . ∞ ∑ n = 1 , 3 , 5 , . . . ∞ n 2 b 2 + ν m 2 a 2 m n ( m 2 a 2 + n 2 b 2 ) 2 sin m π x a sin n π y b {\displaystyle M_{y}={\frac {16q_{0}}{\pi ^{4}}}\sum _{m=1,3,5,...}^{\infty }\sum _{n=1,3,5,...}^{\infty }{\frac {{\frac {n^{2}}{b^{2}}}+\nu {\frac {m^{2}}{a^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} Решение Леви Другой подход был предложен Леви [4] в 1899 году. В этом случае мы начинаем с предполагаемой формы смещения и пытаемся подобрать параметры так, чтобы основное уравнение и граничные условия были удовлетворены. Цель состоит в том, чтобы найти такой, который удовлетворяет граничным условиям при и и, конечно же, основному уравнению . Y m ( y ) {\displaystyle Y_{m}(y)} y = 0 {\displaystyle y=0} y = b {\displaystyle y=b} ∇ 2 ∇ 2 w = q / D {\displaystyle \nabla ^{2}\nabla ^{2}w=q/D}
Предположим, что
w ( x , y ) = ∑ m = 1 ∞ Y m ( y ) sin m π x a . {\displaystyle w(x,y)=\sum _{m=1}^{\infty }Y_{m}(y)\sin {\frac {m\pi x}{a}}\,.} Для пластины, свободно опертой вдоль и граничными условиями являются и . Обратите внимание, что нет никаких изменений в смещении вдоль этих краев, что означает, что и , таким образом сводя граничное условие момента к эквивалентному выражению . x = 0 {\displaystyle x=0} x = a {\displaystyle x=a} w = 0 {\displaystyle w=0} M x x = 0 {\displaystyle M_{xx}=0} ∂ w / ∂ y = 0 {\displaystyle \partial w/\partial y=0} ∂ 2 w / ∂ y 2 = 0 {\displaystyle \partial ^{2}w/\partial y^{2}=0} ∂ 2 w / ∂ x 2 = 0 {\displaystyle \partial ^{2}w/\partial x^{2}=0}
Моменты по краям Рассмотрим случай чистого моментного нагружения. В таком случае и должен удовлетворить . Поскольку мы работаем в прямоугольных декартовых координатах, основное уравнение можно расширить как q = 0 {\displaystyle q=0} w ( x , y ) {\displaystyle w(x,y)} ∇ 2 ∇ 2 w = 0 {\displaystyle \nabla ^{2}\nabla ^{2}w=0}
∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = 0 . {\displaystyle {\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}=0\,.} Подстановка выражения для в основное уравнение дает нам w ( x , y ) {\displaystyle w(x,y)}
∑ m = 1 ∞ [ ( m π a ) 4 Y m sin m π x a − 2 ( m π a ) 2 d 2 Y m d y 2 sin m π x a + d 4 Y m d y 4 sin m π x a ] = 0 {\displaystyle \sum _{m=1}^{\infty }\left[\left({\frac {m\pi }{a}}\right)^{4}Y_{m}\sin {\frac {m\pi x}{a}}-2\left({\frac {m\pi }{a}}\right)^{2}{\cfrac {d^{2}Y_{m}}{dy^{2}}}\sin {\frac {m\pi x}{a}}+{\frac {d^{4}Y_{m}}{dy^{4}}}\sin {\frac {m\pi x}{a}}\right]=0} или
d 4 Y m d y 4 − 2 m 2 π 2 a 2 d 2 Y m d y 2 + m 4 π 4 a 4 Y m = 0 . {\displaystyle {\frac {d^{4}Y_{m}}{dy^{4}}}-2{\frac {m^{2}\pi ^{2}}{a^{2}}}{\cfrac {d^{2}Y_{m}}{dy^{2}}}+{\frac {m^{4}\pi ^{4}}{a^{4}}}Y_{m}=0\,.} Это обыкновенное дифференциальное уравнение, имеющее общее решение
Y m = A m cosh m π y a + B m m π y a cosh m π y a + C m sinh m π y a + D m m π y a sinh m π y a {\displaystyle Y_{m}=A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}+C_{m}\sinh {\frac {m\pi y}{a}}+D_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}} где – константы, которые можно определить из граничных условий. Поэтому решение перемещения имеет вид A m , B m , C m , D m {\displaystyle A_{m},B_{m},C_{m},D_{m}}
w ( x , y ) = ∑ m = 1 ∞ [ ( A m + B m m π y a ) cosh m π y a + ( C m + D m m π y a ) sinh m π y a ] sin m π x a . {\displaystyle w(x,y)=\sum _{m=1}^{\infty }\left[\left(A_{m}+B_{m}{\frac {m\pi y}{a}}\right)\cosh {\frac {m\pi y}{a}}+\left(C_{m}+D_{m}{\frac {m\pi y}{a}}\right)\sinh {\frac {m\pi y}{a}}\right]\sin {\frac {m\pi x}{a}}\,.} Выберем систему координат такую, чтобы границы пластинки находились в точках и (так же, как и раньше) и в (а не и ). Тогда моментные граничные условия на границах равны x = 0 {\displaystyle x=0} x = a {\displaystyle x=a} y = ± b / 2 {\displaystyle y=\pm b/2} y = 0 {\displaystyle y=0} y = b {\displaystyle y=b} y = ± b / 2 {\displaystyle y=\pm b/2}
w = 0 , − D ∂ 2 w ∂ y 2 | y = b / 2 = f 1 ( x ) , − D ∂ 2 w ∂ y 2 | y = − b / 2 = f 2 ( x ) {\displaystyle w=0\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr |}_{y=b/2}=f_{1}(x)\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr |}_{y=-b/2}=f_{2}(x)} где – известные функции. Решение можно найти, применив эти граничные условия. Мы можем показать, что для симметричного случая, когда f 1 ( x ) , f 2 ( x ) {\displaystyle f_{1}(x),f_{2}(x)}
M y y | y = − b / 2 = M y y | y = b / 2 {\displaystyle M_{yy}{\Bigr |}_{y=-b/2}=M_{yy}{\Bigr |}_{y=b/2}} и
f 1 ( x ) = f 2 ( x ) = ∑ m = 1 ∞ E m sin m π x a {\displaystyle f_{1}(x)=f_{2}(x)=\sum _{m=1}^{\infty }E_{m}\sin {\frac {m\pi x}{a}}} у нас есть
w ( x , y ) = a 2 2 π 2 D ∑ m = 1 ∞ E m m 2 cosh α m sin m π x a ( α m tanh α m cosh m π y a − m π y a sinh m π y a ) {\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\cosh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\tanh \alpha _{m}\cosh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}\right)} где
α m = m π b 2 a . {\displaystyle \alpha _{m}={\frac {m\pi b}{2a}}\,.} Аналогично для антисимметричного случая, когда
M y y | y = − b / 2 = − M y y | y = b / 2 {\displaystyle M_{yy}{\Bigr |}_{y=-b/2}=-M_{yy}{\Bigr |}_{y=b/2}} у нас есть
w ( x , y ) = a 2 2 π 2 D ∑ m = 1 ∞ E m m 2 sinh α m sin m π x a ( α m coth α m sinh m π y a − m π y a cosh m π y a ) . {\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\sinh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\coth \alpha _{m}\sinh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}\right)\,.} Мы можем совмещать симметричные и антисимметричные решения, чтобы получить более общие решения.
Просто опирающаяся пластина с равномерно распределенной нагрузкой Для равномерно распределенной нагрузки имеем
q ( x , y ) = q 0 {\displaystyle q(x,y)=q_{0}} Прогиб свободно опертой пластины с центром при равномерно распределенной нагрузке определяется выражением ( a 2 , 0 ) {\displaystyle \left({\frac {a}{2}},0\right)}
w ( x , y ) = q 0 a 4 D ∑ m = 1 , 3 , 5 , . . . ∞ ( A m cosh m π y a + B m m π y a sinh m π y a + G m ) sin m π x a where A m = − 2 ( α m tanh α m + 2 ) π 5 m 5 cosh α m B m = 2 π 5 m 5 cosh α m G m = 4 π 5 m 5 and α m = m π b 2 a {\displaystyle {\begin{aligned}&w(x,y)={\frac {q_{0}a^{4}}{D}}\sum _{m=1,3,5,...}^{\infty }\left(A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}+G_{m}\right)\sin {\frac {m\pi x}{a}}\\\\&{\begin{aligned}{\text{where}}\quad &A_{m}=-{\frac {2\left(\alpha _{m}\tanh \alpha _{m}+2\right)}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&B_{m}={\frac {2}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&G_{m}={\frac {4}{\pi ^{5}m^{5}}}\\\\{\text{and}}\quad &\alpha _{m}={\frac {m\pi b}{2a}}\end{aligned}}\end{aligned}}} Изгибающие моменты на единицу длины пластины определяются выражением
M x = − q 0 π 2 a 2 ∑ m = 1 , 3 , 5 , . . . ∞ m 2 ( ( ( ν − 1 ) A m + 2 ν B m ) cosh m π y a + ( ν − 1 ) B m m π y a sinh m π y a − G m ) sin m π x a {\displaystyle M_{x}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(\nu -1\right)A_{m}+2\nu B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(\nu -1\right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-G_{m}\right)\sin {\frac {m\pi x}{a}}} M y = − q 0 π 2 a 2 ∑ m = 1 , 3 , 5 , . . . ∞ m 2 ( ( ( 1 − ν ) A m + 2 B m ) cosh m π y a + ( 1 − ν ) B m m π y a sinh m π y a − ν G m ) sin m π x a {\displaystyle M_{y}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(1-\nu \right)A_{m}+2B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(1-\nu \right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-\nu G_{m}\right)\sin {\frac {m\pi x}{a}}} Равномерная и симметричная моментная нагрузка Для частного случая, когда нагрузка симметрична и момент однороден, мы имеем при , y = ± b / 2 {\displaystyle y=\pm b/2}
M y y = f 1 ( x ) = 4 M 0 π ∑ m = 1 ∞ 1 2 m − 1 sin ( 2 m − 1 ) π x a . {\displaystyle M_{yy}=f_{1}(x)={\frac {4M_{0}}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{2m-1}}\,\sin {\frac {(2m-1)\pi x}{a}}\,.} Результирующее смещение
w ( x , y ) = 2 M 0 a 2 π 3 D ∑ m = 1 ∞ 1 ( 2 m − 1 ) 3 cosh α m sin ( 2 m − 1 ) π x a × [ α m tanh α m cosh ( 2 m − 1 ) π y a − ( 2 m − 1 ) π y a sinh ( 2 m − 1 ) π y a ] {\displaystyle {\begin{aligned}&w(x,y)={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&~~\left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}} где
α m = π ( 2 m − 1 ) b 2 a . {\displaystyle \alpha _{m}={\frac {\pi (2m-1)b}{2a}}\,.} Изгибающие моменты и поперечные силы, соответствующие смещению, равны w {\displaystyle w}
M x x = − D ( ∂ 2 w ∂ x 2 + ν ∂ 2 w ∂ y 2 ) = 2 M 0 ( 1 − ν ) π ∑ m = 1 ∞ 1 ( 2 m − 1 ) cosh α m × sin ( 2 m − 1 ) π x a × [ − ( 2 m − 1 ) π y a sinh ( 2 m − 1 ) π y a + { 2 ν 1 − ν + α m tanh α m } cosh ( 2 m − 1 ) π y a ] M x y = ( 1 − ν ) D ∂ 2 w ∂ x ∂ y = − 2 M 0 ( 1 − ν ) π ∑ m = 1 ∞ 1 ( 2 m − 1 ) cosh α m × cos ( 2 m − 1 ) π x a × [ ( 2 m − 1 ) π y a cosh ( 2 m − 1 ) π y a + ( 1 − α m tanh α m ) sinh ( 2 m − 1 ) π y a ] Q z x = ∂ M x x ∂ x − ∂ M x y ∂ y = 4 M 0 a ∑ m = 1 ∞ 1 cosh α m × cos ( 2 m − 1 ) π x a cosh ( 2 m − 1 ) π y a . {\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\sin {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m}\tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1)\pi y}{a}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {4M_{0}}{a}}\sum _{m=1}^{\infty }{\frac {1}{\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\,.\end{aligned}}} Стрессы
σ x x = 12 z h 3 M x x and σ z x = 1 κ h Q z x ( 1 − 4 z 2 h 2 ) . {\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.} Гибка цилиндрической пластины Цилиндрический изгиб возникает, когда прямоугольная пластина, имеющая размеры , где и толщина мала, подвергается воздействию равномерно распределенной нагрузки, перпендикулярной плоскости пластины. Такая пластина принимает форму поверхности цилиндра. a × b × h {\displaystyle a\times b\times h} a ≪ b {\displaystyle a\ll b} h {\displaystyle h}
Просто поддерживаемая пластина с закрепленными в осевом направлении концами Для свободно опертой пластины при цилиндрическом изгибе со свободно вращающимися, но неподвижными краями . Решения для цилиндрического изгиба можно найти с помощью методов Навье и Леви. x 1 {\displaystyle x_{1}}
Гибка толстых пластин Миндлина Для толстых пластин необходимо учитывать влияние сдвига по толщине на ориентацию нормали к срединной поверхности после деформации. Теория Раймонда Д. Миндлина предлагает один из подходов к определению деформации и напряжений в таких пластинах. Решения теории Миндлина могут быть получены из эквивалентных решений Кирхгофа-Лява с использованием канонических соотношений. [5]
Основные уравнения Каноническое основное уравнение для изотропных толстых пластин можно выразить как [5]
∇ 2 ( M − B 1 + ν q ) = − q κ G h ( ∇ 2 w + M D ) = − ( 1 − B c 2 1 + ν ) q ∇ 2 ( ∂ φ 1 ∂ x 2 − ∂ φ 2 ∂ x 1 ) = c 2 ( ∂ φ 1 ∂ x 2 − ∂ φ 2 ∂ x 1 ) {\displaystyle {\begin{aligned}&\nabla ^{2}\left({\mathcal {M}}-{\frac {\mathcal {B}}{1+\nu }}\,q\right)=-q\\&\kappa Gh\left(\nabla ^{2}w+{\frac {\mathcal {M}}{D}}\right)=-\left(1-{\cfrac {{\mathcal {B}}c^{2}}{1+\nu }}\right)q\\&\nabla ^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)=c^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)\end{aligned}}} где - приложенная поперечная нагрузка, - модуль сдвига,
- жесткость при изгибе, - толщина пластины, - поправочный коэффициент сдвига, - модуль Юнга, - коэффициент Пуассона, и q {\displaystyle q} G {\displaystyle G} D = E h 3 / [ 12 ( 1 − ν 2 ) ] {\displaystyle D=Eh^{3}/[12(1-\nu ^{2})]} h {\displaystyle h} c 2 = 2 κ G h / [ D ( 1 − ν ) ] {\displaystyle c^{2}=2\kappa Gh/[D(1-\nu )]} κ {\displaystyle \kappa } E {\displaystyle E} ν {\displaystyle \nu }
M = D [ A ( ∂ φ 1 ∂ x 1 + ∂ φ 2 ∂ x 2 ) − ( 1 − A ) ∇ 2 w ] + 2 q 1 − ν 2 B . {\displaystyle {\mathcal {M}}=D\left[{\mathcal {A}}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)-(1-{\mathcal {A}})\nabla ^{2}w\right]+{\frac {2q}{1-\nu ^{2}}}{\mathcal {B}}\,.} В теории Миндлина – поперечное смещение срединной поверхности пластины и величины и – повороты нормали срединной поверхности вокруг осей и - соответственно. Каноническими параметрами этой теории являются и . Поправочный коэффициент сдвига обычно имеет значение . w {\displaystyle w} φ 1 {\displaystyle \varphi _{1}} φ 2 {\displaystyle \varphi _{2}} x 2 {\displaystyle x_{2}} x 1 {\displaystyle x_{1}} A = 1 {\displaystyle {\mathcal {A}}=1} B = 0 {\displaystyle {\mathcal {B}}=0} κ {\displaystyle \kappa } 5 / 6 {\displaystyle 5/6}
Решения основных уравнений можно найти, если знать соответствующие решения Кирхгофа-Лява, используя соотношения
w = w K + M K κ G h ( 1 − B c 2 2 ) − Φ + Ψ φ 1 = − ∂ w K ∂ x 1 − 1 κ G h ( 1 − 1 A − B c 2 2 ) Q 1 K + ∂ ∂ x 1 ( D κ G h A ∇ 2 Φ + Φ − Ψ ) + 1 c 2 ∂ Ω ∂ x 2 φ 2 = − ∂ w K ∂ x 2 − 1 κ G h ( 1 − 1 A − B c 2 2 ) Q 2 K + ∂ ∂ x 2 ( D κ G h A ∇ 2 Φ + Φ − Ψ ) + 1 c 2 ∂ Ω ∂ x 1 {\displaystyle {\begin{aligned}w&=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\left(1-{\frac {{\mathcal {B}}c^{2}}{2}}\right)-\Phi +\Psi \\\varphi _{1}&=-{\frac {\partial w^{K}}{\partial x_{1}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{1}^{K}+{\frac {\partial }{\partial x_{1}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{2}}}\\\varphi _{2}&=-{\frac {\partial w^{K}}{\partial x_{2}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{2}^{K}+{\frac {\partial }{\partial x_{2}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{1}}}\end{aligned}}} где – смещение, предсказанное для пластины Кирхгофа-Лява, – бигармоническая функция такая, что , – функция, удовлетворяющая уравнению Лапласа, и w K {\displaystyle w^{K}} Φ {\displaystyle \Phi } ∇ 2 ∇ 2 Φ = 0 {\displaystyle \nabla ^{2}\nabla ^{2}\Phi =0} Ψ {\displaystyle \Psi } ∇ 2 Ψ = 0 {\displaystyle \nabla ^{2}\Psi =0}
M = M K + B 1 + ν q + D ∇ 2 Φ ; M K := − D ∇ 2 w K Q 1 K = − D ∂ ∂ x 1 ( ∇ 2 w K ) , Q 2 K = − D ∂ ∂ x 2 ( ∇ 2 w K ) Ω = ∂ φ 1 ∂ x 2 − ∂ φ 2 ∂ x 1 , ∇ 2 Ω = c 2 Ω . {\displaystyle {\begin{aligned}{\mathcal {M}}&={\mathcal {M}}^{K}+{\frac {\mathcal {B}}{1+\nu }}\,q+D\nabla ^{2}\Phi ~;~~{\mathcal {M}}^{K}:=-D\nabla ^{2}w^{K}\\Q_{1}^{K}&=-D{\frac {\partial }{\partial x_{1}}}\left(\nabla ^{2}w^{K}\right)~,~~Q_{2}^{K}=-D{\frac {\partial }{\partial x_{2}}}\left(\nabla ^{2}w^{K}\right)\\\Omega &={\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}~,~~\nabla ^{2}\Omega =c^{2}\Omega \,.\end{aligned}}} Просто опирающиеся прямоугольные пластины Для свободно опертых пластин сумма моментов Маркуса обращается в нуль, т.е.
M = 1 1 + ν ( M 11 + M 22 ) = D ( ∂ φ 1 ∂ x 1 + ∂ φ 2 ∂ x 2 ) = 0 . {\displaystyle {\mathcal {M}}={\frac {1}{1+\nu }}(M_{11}+M_{22})=D\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)=0\,.} Это почти уравнение Лапласа для w[ссылка 6]. В этом случае функции , , обращаются в нуль и решение Миндлина связано с соответствующим решением Кирхгофа соотношением Φ {\displaystyle \Phi } Ψ {\displaystyle \Psi } Ω {\displaystyle \Omega }
w = w K + M K κ G h . {\displaystyle w=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\,.} Изгиб консольных пластин Райсснера-Штайна Теория Рейсснера-Штайна для консольных пластин [6] приводит к следующим связанным обыкновенным дифференциальным уравнениям для консольной пластины с сосредоточенной концевой нагрузкой при . q x ( y ) {\displaystyle q_{x}(y)} x = a {\displaystyle x=a}
b D d 4 w x d x 4 = 0 b 3 D 12 d 4 θ x d x 4 − 2 b D ( 1 − ν ) d 2 θ x d x 2 = 0 {\displaystyle {\begin{aligned}&bD{\frac {\mathrm {d} ^{4}w_{x}}{\mathrm {d} x^{4}}}=0\\&{\frac {b^{3}D}{12}}\,{\frac {\mathrm {d} ^{4}\theta _{x}}{\mathrm {d} x^{4}}}-2bD(1-\nu ){\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\end{aligned}}} а граничные условия при равны x = a {\displaystyle x=a}
b D d 3 w x d x 3 + q x 1 = 0 , b 3 D 12 d 3 θ x d x 3 − 2 b D ( 1 − ν ) d θ x d x + q x 2 = 0 b D d 2 w x d x 2 = 0 , b 3 D 12 d 2 θ x d x 2 = 0 . {\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+q_{x1}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}-2bD(1-\nu ){\cfrac {d\theta _{x}}{dx}}+q_{x2}=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\,.\end{aligned}}} Решение этой системы двух ОДУ дает
w x ( x ) = q x 1 6 b D ( 3 a x 2 − x 3 ) θ x ( x ) = q x 2 2 b D ( 1 − ν ) [ x − 1 ν b ( sinh ( ν b a ) cosh [ ν b ( x − a ) ] + tanh [ ν b ( x − a ) ] ) ] {\displaystyle {\begin{aligned}w_{x}(x)&={\frac {q_{x1}}{6bD}}\,(3ax^{2}-x^{3})\\\theta _{x}(x)&={\frac {q_{x2}}{2bD(1-\nu )}}\left[x-{\frac {1}{\nu _{b}}}\,\left({\frac {\sinh(\nu _{b}a)}{\cosh[\nu _{b}(x-a)]}}+\tanh[\nu _{b}(x-a)]\right)\right]\end{aligned}}} где . Изгибающие моменты и поперечные силы, соответствующие смещению, равны ν b = 24 ( 1 − ν ) / b {\displaystyle \nu _{b}={\sqrt {24(1-\nu )}}/b} w = w x + y θ x {\displaystyle w=w_{x}+y\theta _{x}}
M x x = − D ( ∂ 2 w ∂ x 2 + ν ∂ 2 w ∂ y 2 ) = q x 1 ( x − a b ) − [ 3 y q x 2 b 3 ν b cosh 3 [ ν b ( x − a ) ] ] × [ 6 sinh ( ν b a ) − sinh [ ν b ( 2 x − a ) ] + sinh [ ν b ( 2 x − 3 a ) ] + 8 sinh [ ν b ( x − a ) ] ] M x y = ( 1 − ν ) D ∂ 2 w ∂ x ∂ y = q x 2 2 b [ 1 − 2 + cosh [ ν b ( x − 2 a ) ] − cosh [ ν b x ] 2 cosh 2 [ ν b ( x − a ) ] ] Q z x = ∂ M x x ∂ x − ∂ M x y ∂ y = q x 1 b − ( 3 y q x 2 2 b 3 cosh 4 [ ν b ( x − a ) ] ) × [ 32 + cosh [ ν b ( 3 x − 2 a ) ] − cosh [ ν b ( 3 x − 4 a ) ] − 16 cosh [ 2 ν b ( x − a ) ] + 23 cosh [ ν b ( x − 2 a ) ] − 23 cosh ( ν b x ) ] . {\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=q_{x1}\left({\frac {x-a}{b}}\right)-\left[{\frac {3yq_{x2}}{b^{3}\nu _{b}\cosh ^{3}[\nu _{b}(x-a)]}}\right]\times \\&\quad \left[6\sinh(\nu _{b}a)-\sinh[\nu _{b}(2x-a)]+\sinh[\nu _{b}(2x-3a)]+8\sinh[\nu _{b}(x-a)]\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&={\frac {q_{x2}}{2b}}\left[1-{\frac {2+\cosh[\nu _{b}(x-2a)]-\cosh[\nu _{b}x]}{2\cosh ^{2}[\nu _{b}(x-a)]}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {q_{x1}}{b}}-\left({\frac {3yq_{x2}}{2b^{3}\cosh ^{4}[\nu _{b}(x-a)]}}\right)\times \left[32+\cosh[\nu _{b}(3x-2a)]-\cosh[\nu _{b}(3x-4a)]\right.\\&\qquad \left.-16\cosh[2\nu _{b}(x-a)]+23\cosh[\nu _{b}(x-2a)]-23\cosh(\nu _{b}x)\right]\,.\end{aligned}}} Стрессы
σ x x = 12 z h 3 M x x and σ z x = 1 κ h Q z x ( 1 − 4 z 2 h 2 ) . {\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.} Если приложенная нагрузка на краю постоянна, мы восстанавливаем решения для балки под сосредоточенной концевой нагрузкой. Если приложенная нагрузка является линейной функцией от , то y {\displaystyle y}
q x 1 = ∫ − b / 2 b / 2 q 0 ( 1 2 − y b ) d y = b q 0 2 ; q x 2 = ∫ − b / 2 b / 2 y q 0 ( 1 2 − y b ) d y = − b 2 q 0 12 . {\displaystyle q_{x1}=\int _{-b/2}^{b/2}q_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y={\frac {bq_{0}}{2}}~;~~q_{x2}=\int _{-b/2}^{b/2}yq_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y=-{\frac {b^{2}q_{0}}{12}}\,.} Смотрите также Рекомендации ^ Редди, Дж. Н., 2007, Теория и анализ упругих пластин и оболочек , CRC Press, Тейлор и Фрэнсис. ^ Тимошенко С. и Войновский-Кригер С. (1959), Теория пластин и оболочек , McGraw-Hill, Нью-Йорк. ^ Кук, Р.Д. и др., 2002, Концепции и приложения анализа методом конечных элементов , John Wiley & Sons. ^ Леви, М., 1899, Comptes rendues , vol. 129, стр. 535-539. ^ ab Lim, GT и Reddy, JN, 2003, О канонических соотношениях изгиба пластин , International Journal of Solids and Structures, vol. 40, стр. 3039–3067. ^ Э. Рейсснер и М. Штайн. Кручение и поперечный изгиб консольных пластин. Техническая нота 2369, Национальный консультативный комитет по аэронавтике, Вашингтон, 1951 г. 
![{\displaystyle {\cfrac {\partial ^{4}F}{\partial x^{4}}}+2{\cfrac {\partial ^{4}F}{\partial x^{2}\partial y ^{2}}}+{\cfrac {\partial ^{4}F}{\partial y^{4}}}=E\left[\left({\cfrac {\partial ^{2}w}{ \partial x\partial y}}\right)^{2}-{\cfrac {\partial ^{2}w}{\partial x^{2}}}{\cfrac {\partial ^{2}w} {\partial y^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a797f21006ff4d841374f445a8e54ab2b7fb279)
![{\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r} }{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8083e6e16a9118c0afe8bd3c7e1fe841e17334)
![{\displaystyle \sigma _{rr}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{rr}+\nu \varepsilon _{\theta \theta }\right ]~;~~\sigma _{\theta \theta }={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{\theta \theta }+\nu \varepsilon _ {rr}\right]~;~~\sigma _{r\theta }=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3113afbe187db314e19db5772f1fb7ec65d5f2bf)
![{\displaystyle D=2Eh^{3}/[3(1-\nu ^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a71aa263a9aeffc5de8a3eeb37a569a193d2443)
![{\displaystyle {\begin{aligned}\sigma _{rr}&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^{2}-(3+ \nu )r^{2}\right]\\\sigma _{\theta \theta }&=-{\frac {3qz}{32h^{3}}}\left[(1+\nu )a^ {2}-(1+3\nu )r^{2}\right]\\\sigma _{r\theta }&=0\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e9eae0c15eb3c3606cfcbfadf7e523df1069eae)
![{\displaystyle M_{rr}=-{\frac {q}{16}}\left[(1+\nu)a^{2}-(3+\nu)r^{2}\right]~; ~~M_{\theta \theta }=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right ]~;~~M_{r\theta }=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa27857c8e8ae81af9dc56fa29a74b33bc3dad8)
![{\displaystyle \sum _{m=1}^{\infty }\left[\left({\frac {m\pi }{a}}\right)^{4}Y_{m}\sin {\frac {m\pi x}{a}}-2\left({\frac {m\pi }{a}}\right)^{2}{\cfrac {d^{2}Y_{m}}{dy ^{2}}}\sin {\frac {m\pi x}{a}}+{\frac {d^{4}Y_{m}}{dy^{4}}}\sin {\frac { m\pi x}{a}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b7bc6c19d495de8e6086dc8866cf7571b323f9)
![{\ displaystyle w (x, y) = \ sum _ {m = 1} ^ {\ infty } \ left [\ left (A_ {m} + B_ {m} {\ frac {m \ pi y} {a} }\right)\cosh {\frac {m\pi y}{a}}+\left(C_{m}+D_{m}{\frac {m\pi y}{a}}\right)\sinh {\frac {m\pi y}{a}}\right]\sin {\frac {m\pi x}{a}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f35b38c6ddc1b29b74377203666d669c5791b2cc)
![{\displaystyle {\begin{aligned}&w(x,y)={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{m=1}^{ \infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&~~\left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m -1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05bb4b518f750d8e1aafd47fb079065c5c4a5786)
![{\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{ m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\sin {\frac {(2m-1) \pi x}{a}}\,\times \\&~\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m} \tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{xy}&=(1-\nu )D{ \frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m =1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\ pi x}{a}}\,\times \\&~\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y} {a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1 )\pi y}{a}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{ \partial y}}\\&={\frac {4M_{0}}{a}}\sum _{m=1}^{\infty }{\frac {1}{\cosh \alpha _{m} }}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\, .\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b46371a14545a06c6bb677179132a02137a8fbb4)
![{\displaystyle D=Эх^{3}/[12(1-\nu ^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f3bf995e9bb0214179b93d14f38e7e01cf3a671)
![{\displaystyle c^{2}=2\kappa Gh/[D(1-\nu)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc4c3ed836ac15ba7c94c0e0fc3cd9fb1d8825a)
![{\displaystyle {\mathcal {M}}=D\left[{\mathcal {A}}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\ frac {\partial \varphi _{2}}{\partial x_{2}}}\right)-(1- {\mathcal {A}})\nabla ^{2}w\right]+{\frac { 2q}{1-\nu ^{2}}}{\mathcal {B}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c93657927f897412a7df1207325d3a731bfa9fed)
![{\displaystyle {\begin{aligned}w_{x}(x)&={\frac {q_{x1}}{6bD}}\,(3ax^{2}-x^{3})\\\theta _{x}(x)&={\frac {q_{x2}}{2bD(1-\nu )}}\left[x-{\frac {1}{\nu _{b}}}\, \left({\frac {\sinh(\nu _{b}a)}{\cosh[\nu _{b}(xa)]}}+\tanh[\nu _{b}(xa)]\ вправо)\вправо]\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a9eebb0810de812da44e1e62453b7af0aa8dddf)
![{\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=q_{x1}\left({\frac {xa}{b}}\right)-\left[ {\frac {3yq_{x2}}{b^{3}\nu _{b}\cosh ^{3}[\nu _{b}(xa)]}}\right]\times \\&\quad \left[6\sinh(\nu _{b}a)-\sinh[\nu _{b}(2x-a)]+\sinh[\nu _{b}(2x-3a)]+8\ sinh[\nu _{b}(xa)]\right]\\M_{xy}&=(1-\nu )D {\frac {\partial ^{2}w}{\partial x\partial y} }\\&={\frac {q_{x2}}{2b}}\left[1- {\frac {2+\cosh[\nu _{b}(x-2a)]-\cosh[\nu _{b}x]}{2\cosh ^{2}[\nu _{b}(xa)]}}\right]\\Q_{zx}&={\frac {\partial M_{xx}} {\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {q_{x1}}{b}}-\left({\frac {3yq_ {x2}}{2b^{3}\cosh ^{4}[\nu _{b}(xa)]}}\right)\times \left[32+\cosh[\nu _{b}(3x -2a)]-\cosh[\nu _{b}(3x-4a)]\right.\\&\qquad \left.-16\cosh[2\nu _{b}(xa)]+23\ cosh[\nu _{b}(x-2a)]-23\cosh(\nu _{b}x)\right]\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23db4b670f6da6f2f18a0e2419ca828fbc73d657)
