Кривая Бринга

Фундаментальный икосагон с додекадодекаэдрическим графом зеленого цвета и его двойственным фиолетовым цветом. Это частное пятиугольной мозаики четвертого порядка и ее двойственной квадратной мозаики .
Ребра 20-угольников, отмеченные одной и той же буквой, равны.

Кривая Бринга связана с малым звездчатым додекаэдром и додекадодекаэдром . ^[1]

В математике кривая Бринга ( также называемая поверхностью Бринга и, по аналогии с квартикой Клейна , секстикой Бринга ) — это кривая в проективном пространстве , вырезанная однородными уравнениями ${\displaystyle \mathbb {P} ^{4}}$

${\displaystyle v+w+x+y+z=v^{2}+w^{2}+x^{2}+y^{2}+z^{2}=v^{3}+w^{3}+x^{3}+y^{3}+z^{3}=0.}$

Он был назван Кляйном (2003, стр. 157) в честь Эрланда Сэмюэля Бринга, который изучал подобную конструкцию в 1786 году в Promotionschrift, представленном в Лундский университет . Заметим, что корни x _i квинтики Бринга удовлетворяют кривой Бринга, поскольку для ${\displaystyle x^{5}+ax+b=0}$ ${\displaystyle \sum _{i=1}^{5}x_{i}^{k}=0}$ ${\displaystyle k=1,2,3.}$

Группа автоморфизмов кривой — это симметрическая группа S ₅ порядка 120, заданная перестановками 5 координат . Это максимально возможная группа автоморфизмов комплексной кривой рода 4.

Кривая может быть реализована как тройное покрытие сферы, разветвленной в 12 точках, и представляет собой риманову поверхность , связанную с малым звездчатым додекаэдром . Имеет род 4. Полная группа симметрий (включая отражения) представляет собой прямое произведение , имеющее порядок 240. ${\displaystyle S_{5}\times \mathbb {Z} _{2}}$

Фундаментальный домен и систола

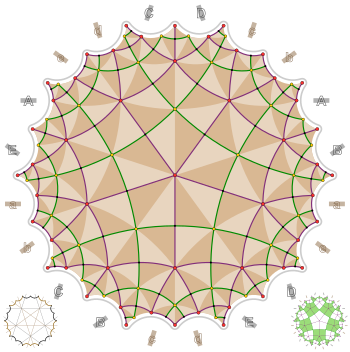
Кривую Бринга можно получить как риманову поверхность путем сопоставления сторон гиперболического икосагона (см. фундаментальный многоугольник ). Идентификационный образец приведен на прилагаемой диаграмме. Икосагон (площадью по теореме Гаусса-Бонне ) можно разбить на мозаику из 240 (2,4,5) треугольников. Действия, переносящие один из этих треугольников в другой, дают полную группу автоморфизмов поверхности (включая отражения). Не считая отражений, мы получаем 120 автоморфизмов, упомянутых во введении. Обратите внимание, что 120 меньше 252, максимального числа автоморфизмов, сохраняющих ориентацию, разрешенных для поверхности рода 4 согласно теореме Гурвица об автоморфизме . Следовательно, поверхность Бринга не является поверхностью Гурвица . Это также говорит нам о том, что не существует поверхности Гурвица рода 4. ${\displaystyle 12\pi }$

Полная группа симметрий имеет следующее представление:

${\displaystyle \langle r,\,s,\,t\,|\,r^{5}=s^{2}=t^{2}=rtrt=stst=(rs)^{4}=(sr^{3}sr^{2})^{2}=e\rangle }$,

где - тождественное действие, - поворот порядка 5 вокруг центра фундаментального многоугольника, - поворот порядка 2 в вершине, где встречаются 4 (2,4,5) треугольника в мозаике, и - отражение в реальном пространстве. линия. Из этой презентации информацию о теории линейного представления группы симметрии поверхности Бринга можно вычислить с помощью GAP . В частности, группа имеет четыре одномерных, четыре четырехмерных, четыре пятимерных и два шестимерных неприводимых представления, и мы имеем ${\displaystyle e}$ ${\displaystyle r}$ ${\displaystyle s}$ ${\displaystyle t}$

${\displaystyle 4(1^{2})+4(4^{2})+4(5^{2})+2(6^{2})=4+64+100+72=240}$

как и ожидалось.

Систола поверхности имеет длину

${\displaystyle 12\sinh ^{-1}\left({\tfrac {1}{2}}{\sqrt {{\tfrac {1}{2}}({\sqrt {5}}-1)}}\right)\approx 4.60318}$

и кратность 20, геодезическая петля такой длины, состоящая из объединенных высот двенадцати из 240 (2,4,5) треугольников. Подобно квартике Клейна , поверхность Бринга не максимизирует длину систолы среди компактных римановых поверхностей в своей топологической категории (то есть поверхностей одного и того же рода), несмотря на максимизацию размера группы автоморфизмов. Систола, по-видимому, максимизируется за счет поверхности, обозначенной М4 в (Schmutz 1993). Длина систолы М4 равна

${\displaystyle 2\cosh ^{-1}\left({\tfrac {1}{2}}(5+3{\sqrt {3}})\right)\approx 4.6245,}$

и имеет кратность 36.

Спектральная теория

О спектральной теории поверхности Бринга известно немного , однако потенциально она может представлять интерес в этой области. Поверхность Больца и квартика Клейна имеют самые большие группы симметрии среди компактных римановых поверхностей постоянной отрицательной кривизны в родах 2 и 3 соответственно, и поэтому было высказано предположение, что они максимизируют первое положительное собственное значение в спектре Лапласа. Существуют убедительные численные доказательства в поддержку этой гипотезы, особенно в случае поверхности Больца, хотя обеспечение строгого доказательства все еще остается открытой проблемой. Следуя этой схеме, можно разумно предположить, что поверхность Бринга максимизирует первое положительное собственное значение лапласиана (среди поверхностей своего топологического класса).

Смотрите также

• Поверхность Больцы
• Клейн квартик
• Поверхность Макбита
• Первая тройка Гурвица

Рекомендации

1. Вебер, Матиас (2005). «Маленький звездчатый додекаэдр Кеплера как риманова поверхность». Пасифик Дж. Математика . Том. 220. стр. 167–182.PDF

• Принеси, Эрланд Сэмюэл; Соммелиус, Свен Густав (1786), Meletemata quædam mathematica circa Transformem æquationem алгебраикарум , Promotionschrift, Лундский университет
• Эдж, WL (1978), «Кривая Бринга», Журнал Лондонского математического общества , 18 (3): 539–545, doi : 10.1112/jlms/s2-18.3.539, ISSN  0024-6107, MR  0518240
• Кляйн, Феликс (2003) [1884], Лекции по икосаэдру и решению уравнений пятой степени, Dover Phoenix Editions, Нью-Йорк: Dover Publications , ISBN 978-0-486-49528-6, МР  0080930
• Риера, Г.; Родригес, Р. (1992), «Матрицы периодов кривой Бринга» (PDF) , Pacific J. Math. , 154 (1): 179–200, doi : 10.2140/pjm.1992.154.179 , MR  1154738
• Шмутц, П. (1993), «Римановы поверхности с кратчайшей геодезической максимальной длины», GAFA , 3 (6): 564–631, doi : 10.1007/BF01896258
• Вебер, Матиас (2005), «Маленький звездчатый додекаэдр Кеплера как риманова поверхность», Pacific J. Math. , 220 : 167–182, doi : 10.2140/pjm.2005.220.167