В криптографии шифр замены — это метод шифрования , при котором единицы открытого текста заменяются зашифрованным текстом определенным образом с помощью ключа; «единицами» могут быть отдельные буквы (наиболее распространенные), пары букв, тройки букв, смеси вышеперечисленного и т. д. Получатель расшифровывает текст, выполняя обратный процесс замены для извлечения исходного сообщения.
Шифры замены можно сравнить с шифрами перестановки . В шифре перестановки единицы открытого текста переставляются в другом и обычно довольно сложном порядке, но сами единицы остаются неизменными. Напротив, в шифре замены единицы открытого текста сохраняются в той же последовательности в шифртексте, но сами единицы изменяются.
Существует несколько различных типов шифров замены. Если шифр работает с отдельными буквами, он называется простым шифром замены ; шифр, работающий с большими группами букв, называется полиграфическим . Моноалфавитный шифр использует фиксированную замену во всем сообщении, тогда как полиалфавитный шифр использует ряд замен в разных позициях в сообщении, где единица из открытого текста сопоставляется с одной из нескольких возможностей в зашифрованном тексте и наоборот.
Первое опубликованное описание того, как взломать простые подстановочные шифры, было дано Аль-Кинди в «Рукописи о расшифровке криптографических сообщений», написанной около 850 г. н. э. Описанный им метод теперь известен как частотный анализ .
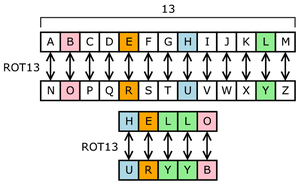
Замена отдельных букв по отдельности — простая замена — может быть продемонстрирована путем записи алфавита в некотором порядке, представляющем замену. Это называется алфавитом замены . Алфавит шифра может быть смещен или обращен (создавая шифры Цезаря и Атбаша соответственно) или перемешан более сложным образом, в этом случае он называется смешанным алфавитом или расстроенным алфавитом . Традиционно смешанные алфавиты могут быть созданы путем первой записи ключевого слова, удаления в нем повторяющихся букв, а затем записи всех оставшихся букв в алфавите в обычном порядке.
Используя эту систему, ключевое слово « зебры » дает нам следующие алфавиты:
Сообщение
бегите немедленно. нас обнаружили!
шифрует для
СИАА ZQ LKBA. ВА ЗОА RFPBLUAOAR!
А ключевое слово « бабушка » дает нам следующие алфавиты:
То же самое сообщение
бегите немедленно. нас обнаружили!
шифрует для
MCDD GS JIAD. WD GPD NHQAJVDPDN!
Обычно шифртекст записывается блоками фиксированной длины, без знаков препинания и пробелов; это делается для того, чтобы скрыть границы слов от открытого текста и избежать ошибок передачи. Эти блоки называются «группами», и иногда в качестве дополнительной проверки указывается «количество групп» (т. е. количество групп). Часто используются группы из пяти букв, которые датируются тем временем, когда сообщения передавались по телеграфу :
СИААЗ КЛКБА ВАЗОА РФПБЛ УАОАР
Если длина сообщения не делится на пять, оно может быть дополнено в конце " нулями ". Это могут быть любые символы, которые расшифровываются как очевидная бессмыслица, так что получатель может легко их обнаружить и отбросить.
Алфавит шифротекста иногда отличается от алфавита открытого текста; например, в шифре pigpen шифротекст состоит из набора символов, полученных из сетки. Например:

Однако такие особенности не оказывают существенного влияния на безопасность схемы — по крайней мере, любой набор странных символов можно преобразовать обратно в алфавит AZ и обрабатывать как обычно.
В списках и каталогах для продавцов иногда используется очень простое шифрование для замены цифр буквами.
Примеры: MAT будет использоваться для обозначения числа 120, PAPR будет использоваться для обозначения числа 5256, а OFTK будет использоваться для обозначения числа 7803.
Хотя традиционный метод ключевых слов для создания смешанного алфавита замены прост, серьезным недостатком является то, что последние буквы алфавита (которые в основном имеют низкую частоту) имеют тенденцию оставаться в конце. Более сильный способ построения смешанного алфавита — это создание алфавита замены полностью случайным образом.
Хотя число возможных алфавитов замены очень велико (26! ≈ 2 88,4 , или около 88 бит ), этот шифр не очень сильный и его легко взломать. При условии, что сообщение имеет разумную длину (см. ниже), криптоаналитик может вывести вероятное значение наиболее распространенных символов, проанализировав распределение частот шифртекста. Это позволяет формировать частичные слова, которые можно предварительно заполнить, постепенно расширяя (частичное) решение (см. анализ частот для демонстрации этого). В некоторых случаях основные слова также можно определить по шаблону их букв; например, английские слова tater , ninth и paper имеют шаблон ABACD . Многие люди разгадывают такие шифры ради развлечения, как в случае с криптограммами- головоломками в газете.
Согласно расстоянию уникальности английского языка , для взлома простой подстановки смешанного алфавита требуется 27,6 букв шифртекста. На практике обычно требуется около 50 букв, хотя некоторые сообщения можно взломать и меньшим количеством, если будут обнаружены необычные закономерности. В других случаях открытый текст можно сделать так, чтобы он имел почти плоское распределение частот, и тогда криптоаналитику потребуются гораздо более длинные открытые тексты.


Одним из некогда распространенных вариантов шифра замены является номенклатор . Названный в честь государственного должностного лица, объявлявшего титулы приезжих сановников, этот шифр использует небольшой кодовый лист, содержащий таблицы замены букв, слогов и слов, иногда омофонические, которые обычно преобразовывали символы в числа. Первоначально часть кода была ограничена именами важных людей, отсюда и название шифра; в более поздние годы он также охватывал многие общие слова и названия мест. Символы для целых слов ( кодовые слова в современном языке) и букв ( шифр в современном языке) не различались в шифртексте. Великий шифр Россиньоля , используемый Людовиком XIV Французским, был одним из них.
Номенклатуры были стандартным продуктом дипломатической переписки, шпионажа и передовых политических заговоров с начала пятнадцатого века до конца восемнадцатого века; большинство заговорщиков были и остаются менее криптографически искушенными. Хотя криптоаналитики правительственной разведки систематически взламывали номенклатуры к середине шестнадцатого века, а более совершенные системы были доступны с 1467 года, обычным ответом на криптоанализ было просто увеличение таблиц. К концу восемнадцатого века, когда система начала умирать, некоторые номенклатуры имели 50 000 символов. [ необходима цитата ]
Тем не менее, не все номенклатуры были взломаны; сегодня криптоанализ архивных шифртекстов остается плодотворной областью исторических исследований .
Ранняя попытка повысить сложность атак частотного анализа на подстановочные шифры состояла в маскировке частот букв открытого текста с помощью омофонии . В этих шифрах буквы открытого текста сопоставляются с более чем одним символом шифртекста. Обычно наиболее часто встречающимся символам открытого текста дается больше эквивалентов, чем менее часто встречающимся буквам. Таким образом, распределение частот выравнивается, что затрудняет анализ.
Поскольку в алфавите шифртекста потребуется более 26 символов, используются различные решения для изобретения более крупных алфавитов. Возможно, самым простым является использование числовой замены «алфавит». Другой метод состоит из простых вариаций существующего алфавита: заглавные буквы, строчные буквы, перевернутые буквы и т. д. Более художественно, хотя и не обязательно более надежно, некоторые омофонические шифры использовали полностью выдуманные алфавиты причудливых символов.
Книжный шифр — это тип омофонического шифра, одним из примеров которого являются шифры Биля . Это история о зарытом сокровище, которая была описана в 1819–1821 годах с использованием зашифрованного текста, который был связан с Декларацией независимости. Здесь каждый символ шифртекста был представлен числом. Число определялось путем взятия открытого символа текста и нахождения слова в Декларации независимости, которое начиналось с этого символа, и использования числового положения этого слова в Декларации независимости в качестве зашифрованной формы этой буквы. Поскольку многие слова в Декларации независимости начинаются с одной и той же буквы, шифрование этого символа может быть любым из чисел, связанных со словами в Декларации независимости, которые начинаются с этой буквы. Расшифровать зашифрованный текстовый символ X (который является числом) так же просто, как найти X-е слово Декларации независимости и использовать первую букву этого слова в качестве расшифрованного символа.
Другой омофонический шифр был описан Шталем [2] [3] и был одной из первых [ требуется цитата ] попыток обеспечить компьютерную безопасность систем данных в компьютерах с помощью шифрования. Шталь построил шифр таким образом, что количество омофонов для данного символа было пропорционально частоте символа, что значительно усложнило частотный анализ.
Франческо I Гонзага , герцог Мантуи , использовал самый ранний известный пример омофонического подстановочного шифра в 1401 году для переписки с неким Симоном де Крема. [4] [5]
Мария, королева Шотландии , находясь в заключении у Елизаветы I, в период с 1578 по 1584 год использовала омофонические шифры с дополнительным шифрованием, используя номенклатор для часто встречающихся префиксов, суффиксов и имен собственных при общении со своими союзниками, включая Мишеля де Кастельно . [6]
Работа Аль-Калькашанди (1355-1418), основанная на более ранней работе Ибн ад-Дурайхима (1312–1359), содержала первое опубликованное обсуждение замены и транспозиции шифров, а также первое описание полиалфавитного шифра, в котором каждой букве открытого текста назначается более одной замены. [7] Полиалфавитные шифры замены были позже описаны в 1467 году Леоне Баттиста Альберти в форме дисков. Иоганнес Тритемий в своей книге Steganographia ( древнегреческое слово , означающее «скрытое письмо») представил теперь более стандартную форму таблицы ( см. ниже; около 1500 года, но опубликовано гораздо позже). Более сложная версия, использующая смешанные алфавиты, была описана в 1563 году Джованни Баттиста делла Порта в его книге De Furtivis Literarum Notis ( лат . «О скрытых символах в письме»).
В полиалфавитном шифре используются несколько шифралфавитов. Для облегчения шифрования все алфавиты обычно записываются в большую таблицу , традиционно называемую tableau . Таблица обычно имеет размер 26×26, так что доступно 26 полных алфавитов шифртекста. Метод заполнения таблицы и выбора следующего алфавита определяет конкретный полиалфавитный шифр. Все такие шифры легче взломать, чем считалось ранее, поскольку подстановочные алфавиты повторяются для достаточно больших открытых текстов.
Одним из самых популярных был шифр Блеза де Виженера . Впервые опубликованный в 1585 году, он считался нераскрываемым до 1863 года и, действительно, обычно назывался le chiffre indéchiffrable ( по-французски «неразборчивый шифр»).
В шифре Виженера первая строка таблицы заполняется копией алфавита открытого текста, а последующие строки просто сдвигаются на одну позицию влево. (Такая простая таблица называется tabula recta и математически соответствует сложению открытого текста и ключевых букв по модулю 26.) Затем используется ключевое слово для выбора используемого алфавита шифртекста. Каждая буква ключевого слова используется по очереди, а затем они повторяются снова с самого начала. Так, если ключевое слово «CAT», первая буква открытого текста шифруется под алфавитом «C», вторая под «A», третья под «T», четвертая снова под «C» и так далее, или если ключевое слово «RISE», первая буква открытого текста шифруется под алфавитом «R», вторая под «I», третья под «S», четвертая под «E» и так далее. На практике ключи Виженера часто представляли собой фразы длиной в несколько слов.
В 1863 году Фридрих Касиски опубликовал метод (вероятно, тайно и независимо открытый до Крымской войны Чарльзом Бэббиджем ), который позволял вычислять длину ключевого слова в зашифрованном по Виженеру сообщении. Как только это было сделано, буквы шифртекста, зашифрованные в одном и том же алфавите, можно было выбрать и атаковать по отдельности как ряд полунезависимых простых замен — усложняя это тем фактом, что в пределах одного алфавита буквы были разделены и не образовывали полных слов, но упрощая тем фактом, что обычно использовалась tabula recta .
Таким образом, даже сегодня шифр типа Виженера теоретически должен быть трудно взломан, если в таблице используются смешанные алфавиты, если ключевое слово является случайным и если общая длина шифротекста меньше длины ключевого слова, умноженной на 27,67. [8] Эти требования редко понимаются на практике, и поэтому безопасность зашифрованных сообщений Виженера обычно ниже, чем могла бы быть.
Другие известные полиалфавиты включают в себя:
Современные потоковые шифры можно также рассматривать, с достаточно абстрактной точки зрения, как форму полиалфавитного шифра, в котором все усилия направлены на то, чтобы сделать ключевой поток как можно более длинным и непредсказуемым.
В полиграфическом шифре замены буквы открытого текста заменяются большими группами, а не заменяются по отдельности. Первое преимущество заключается в том, что распределение частот гораздо более плоское, чем у отдельных букв (хотя на самом деле не плоское в реальных языках; например, «OS» встречается гораздо чаще, чем «RÑ» в испанском языке). Во-вторых, большее количество символов требует соответственно большего объема шифртекста для продуктивного анализа частот букв.
Для замены пар букв потребовался бы алфавит замены длиной 676 символов ( ). В том же De Furtivis Literarum Notis , упомянутом выше, делла Порта фактически предложил такую систему с таблицей 20 x 20 (для 20 букв итальянского/латинского алфавита, которые он использовал), заполненной 400 уникальными глифами . Однако система была непрактичной и, вероятно, никогда не использовалась.
Самым ранним практическим диграфическим шифром (парная замена) был так называемый шифр Плейфера , изобретенный сэром Чарльзом Уитстоном в 1854 году. В этом шифре сетка 5 x 5 заполняется буквами смешанного алфавита (две буквы, обычно I и J, объединены). Затем диграфическая замена моделируется путем взятия пар букв в качестве двух углов прямоугольника и использования двух других углов в качестве шифртекста (см. основную статью о шифре Плейфера для получения схемы). Специальные правила обрабатывают двойные буквы и пары, попадающие в одну строку или столбец. Плейфер использовался в военных целях с англо- бурской войны до Второй мировой войны .
Несколько других практических полиграфических шифров были введены в 1901 году Феликсом Деластелем , включая двураздельный и четырехугольный шифры (оба диграфические), а также трехраздельный шифр (вероятно, первый практический триграфический шифр).
Шифр Хилла , изобретенный в 1929 году Лестером С. Хиллом , представляет собой полиграфическую замену, которая может объединять гораздо большие группы букв одновременно с использованием линейной алгебры . Каждая буква рассматривается как цифра в основании 26 : A = 0, B = 1 и т. д. (В одном из вариантов добавляются 3 дополнительных символа, чтобы сделать основание простым . ) Затем блок из n букв рассматривается как вектор из n измерений и умножается на матрицу anxn по модулю 26. Компоненты матрицы являются ключом и должны быть случайными при условии, что матрица обратима в (чтобы гарантировать возможность расшифровки). Механическая версия шифра Хилла размерности 6 была запатентована в 1929 году. [9]
Шифр Хилла уязвим к атаке с известным открытым текстом , поскольку он полностью линейный , поэтому его необходимо объединить с каким-то нелинейным шагом, чтобы победить эту атаку. Сочетание все более и более слабых линейных диффузионных шагов, таких как шифр Хилла, с нелинейными шагами подстановки в конечном итоге приводит к сети подстановки-перестановки (например, шифр Фейстеля ), поэтому возможно — с этой крайней точки зрения — рассматривать современные блочные шифры как тип полиграфической подстановки.

Между Первой мировой войной и широкой доступностью компьютеров (для некоторых правительств это было примерно в 1950-х или 1960-х годах; для других организаций это было десятилетие или более позднее; для отдельных лиц это было не ранее 1975 года), механические реализации полиалфавитных подстановочных шифров широко использовались. Несколько изобретателей имели схожие идеи примерно в то же время, и роторные шифровальные машины были запатентованы четыре раза в 1919 году. Наиболее важной из полученных машин была Enigma , особенно в версиях, используемых немецкими военными примерно с 1930 года. Союзники также разработали и использовали роторные машины (например, SIGABA и Typex ).
Все они были похожи тем, что заменяемая буква выбиралась электрически из огромного количества возможных комбинаций, полученных в результате вращения нескольких буквенных дисков. Поскольку один или несколько дисков вращались механически с каждой зашифрованной буквой открытого текста, количество используемых алфавитов было астрономическим. Ранние версии этих машин, тем не менее, были взломаны. Уильям Ф. Фридман из SIS армии США рано обнаружил уязвимости в роторной машине Хеберна , а Диллвин Нокс из GC&CS решил версии машины Enigma (те, которые не имели «коммутационной панели») задолго до начала Второй мировой войны . Трафик, защищенный по существу всеми немецкими военными Enigma, был взломан криптоаналитиками союзников, в первую очередь из Блетчли-Парка , начиная с варианта немецкой армии, использовавшегося в начале 1930-х годов. Эта версия была взломана вдохновенным математическим прозрением Мариана Реевского в Польше .
Насколько известно общественности, ни одно сообщение, защищенное машинами SIGABA и Typex, не было взломано ни в то время, когда эти системы находились в эксплуатации, ни в какой форме.
Один из типов шифра замены, одноразовый блокнот , является уникальным. Он был изобретен ближе к концу Первой мировой войны Гилбертом Вернамом и Джозефом Моборном в США. Его невзламываемость была математически доказана Клодом Шенноном , вероятно, во время Второй мировой войны ; его работа была впервые опубликована в конце 1940-х годов. В своей наиболее распространенной реализации одноразовый блокнот можно назвать шифром замены только с необычной точки зрения; как правило, буква открытого текста объединяется (не заменяется) каким-либо образом (например, XOR ) с символом ключевого материала в этой позиции.
Одноразовый блокнот в большинстве случаев непрактичен, поскольку требует, чтобы ключевой материал был такой же длины, как и открытый текст, фактически случайным , использовался один раз и только один раз и хранился в полной тайне от всех, кроме отправителя и предполагаемого получателя. Когда эти условия нарушаются, даже незначительно, одноразовый блокнот больше не является невзламываемым. Советские сообщения одноразового блокнота, отправленные из США в течение короткого времени во время Второй мировой войны, использовали неслучайный ключевой материал. Американские криптоаналитики, начиная с конца 40-х годов, смогли полностью или частично взломать несколько тысяч сообщений из нескольких сотен тысяч. (См. проект Venona )
В механическом исполнении, подобно оборудованию Rockex , одноразовый блокнот использовался для сообщений, отправляемых по горячей линии Москва - Вашингтон , установленной после Карибского кризиса .
Подстановочные шифры, обсуждавшиеся выше, особенно старые ручные шифры с карандашом и бумагой, больше не используются всерьез. Однако криптографическая концепция подстановки продолжается и сегодня. С абстрактной точки зрения современные бит-ориентированные блочные шифры (например, DES или AES ) можно рассматривать как подстановочные шифры на большом двоичном алфавите. Кроме того, блочные шифры часто включают в себя меньшие таблицы подстановки, называемые S-boxes . См. также сеть подстановки–перестановки .