Тормозная способность (излучение частиц)

Сила торможения, действующая на заряженные частицы из-за взаимодействия с веществом

В ядерной физике и физике материалов тормозная способность — это замедляющая сила, действующая на заряженные частицы , как правило, альфа- и бета-частицы , из-за взаимодействия с веществом , что приводит к потере кинетической энергии частицы . ^{[1] [2]} Тормозная способность также интерпретируется как скорость, с которой материал поглощает кинетическую энергию заряженной частицы . Ее применение важно в широком спектре термодинамических областей, таких как защита от радиации , ионная имплантация и ядерная медицина . ^[3]

График, показывающий взаимосвязь между радиоактивностью и обнаруженным ионизирующим излучением

Определение и кривая Брэгга

Как заряженные, так и незаряженные частицы теряют энергию при прохождении через вещество. В большинстве случаев ниже рассматриваются положительные ионы . Тормозная способность зависит от типа и энергии излучения и от свойств материала, через который оно проходит. Поскольку для образования пары ионов (обычно положительного иона и (отрицательного) электрона) требуется фиксированное количество энергии (например, 33,97 эВ в сухом воздухе ^{[4] : 305} ), число ионизаций на длину пути пропорционально тормозной способности. Тормозная способность материала численно равна потере энергии E на единицу длины пути, x :

${\displaystyle S(E)=-dE/dx}$

Знак минус делает S положительным.

Кривая Брэгга для альфа-частиц с энергией 5,49 МэВ в воздухе

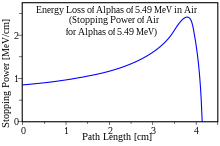
Сила обычно увеличивается к концу диапазона и достигает максимума, пика Брэгга , незадолго до того, как энергия падает до нуля. Кривая, описывающая силу как функцию глубины материала, называется кривой Брэгга . Это имеет большое практическое значение для лучевой терапии .

Уравнение выше определяет линейную тормозную способность , которая в международной системе выражается в Н , но обычно указывается в других единицах, таких как МэВ / мм или подобных. Если вещество сравнивается в газообразной и твердой форме, то линейные тормозные способности двух состояний сильно различаются просто из-за разной плотности. Поэтому часто делят силу на плотность материала, чтобы получить массовую тормозную способность , которая в международной системе выражается в ^м4 / с2 , ^но обычно находится в единицах, таких как МэВ/(мг/см2 ⁾ или подобных. Тогда массовая тормозная способность очень мало зависит от плотности материала.

На рисунке показано, как тормозная способность альфа-частиц с энергией 5,49 МэВ увеличивается по мере того, как частица проходит через воздух, пока не достигает максимума. Эта энергия соответствует энергии альфа-частиц, излучаемых естественным радиоактивным газом радоном ( ²²² Rn), который присутствует в воздухе в ничтожных количествах.

Средний диапазон можно рассчитать путем интегрирования обратной тормозной способности по энергии: ^[5]

${\displaystyle \Delta x=\int _{0}^{E_{0}}{\frac {1}{S(E)}}\,dE}$

где:

E ₀ — начальная кинетическая энергия частицы.

Δ x — это диапазон «приближения непрерывного замедления (CSDA)» и

S ( E ) — линейная тормозная способность.

Выделившуюся энергию можно получить путем интегрирования тормозной способности по всей длине пути иона при его движении в материале.

Электронное, ядерное и радиационное торможение

Электронное торможение относится к замедлению иона-снаряда из-за неупругих столкновений между связанными электронами в среде и ионом, движущимся через нее. Термин неупругое используется для обозначения того, что энергия теряется в ходе процесса (столкновения могут приводить как к возбуждению связанных электронов среды, так и к возбуждению электронного облака иона). Линейная электронная тормозная способность идентична неограниченной линейной передаче энергии .

Вместо передачи энергии некоторые модели рассматривают электронную тормозную способность как передачу импульса между электронным газом и энергичным ионом. Это согласуется с результатом Бете в диапазоне высоких энергий. ^[6]

Поскольку число столкновений иона с электронами велико, а зарядовое состояние иона при прохождении через среду может часто меняться, очень сложно описать все возможные взаимодействия для всех возможных зарядовых состояний ионов. Вместо этого электронная тормозная способность часто задается как простая функция энергии, которая является средним значением, взятым по всем процессам потери энергии для различных зарядовых состояний. Ее можно теоретически определить с точностью до нескольких % в диапазоне энергий выше нескольких сотен кэВ на нуклон из теоретических расчетов, наиболее известной из которых является формула Бете . При энергиях ниже примерно 100 кэВ на нуклон становится сложнее определить электронное торможение с помощью аналитических моделей. ^{[7] Недавно} теория функционала плотности, зависящая от времени, в реальном времени была успешно использована для точного определения электронного торможения для различных систем ионов-мишеней в широком диапазоне энергий, включая режим низкой энергии. ^{[8] [9]} ${\displaystyle F_{e}(E)}$

Электронная и ядерная тормозная способность для ионов алюминия в алюминии в зависимости от энергии частиц на нуклон. Максимум кривой ядерного торможения обычно достигается при энергиях порядка 1 кэВ на нуклон .

Графические представления экспериментальных значений электронной тормозной способности для многих ионов во многих веществах были даны Полом. ^[10] Точность различных таблиц торможения была определена с помощью статистических сравнений. ^[11]

Ядерная тормозная способность относится к упругим столкновениям между ионом-снарядом и атомами в образце (устоявшееся обозначение «ядерный» может сбивать с толку, поскольку ядерное торможение не обусловлено ядерными силами, ^[12] но оно призвано отметить, что этот тип торможения включает взаимодействие иона с ядрами в мишени). Если знать форму потенциальной энергии отталкивания между двумя атомами (см. ниже), можно рассчитать ядерную тормозную способность . На рисунке тормозной способности, показанном выше для ионов алюминия в алюминии, ядерное торможение пренебрежимо мало, за исключением самой низкой энергии. Ядерное торможение увеличивается с увеличением массы иона. На рисунке, показанном справа, ядерное торможение больше электронного торможения при низкой энергии. Для очень легких ионов, замедляющихся в тяжелых материалах, ядерное торможение слабее электронного при всех энергиях. ${\displaystyle E(r)}$ ${\displaystyle F_{n}(E)}$

Особенно в области радиационного повреждения в детекторах термин « неионизирующие потери энергии » (NIEL) используется как термин, противоположный линейной передаче энергии (LET), см., например, ссылки ^{[13] [14] [15]} . Поскольку по определению ядерная тормозная способность не включает в себя электронные возбуждения, NIEL и ядерное торможение можно считать одной и той же величиной при отсутствии ядерных реакций.

Таким образом, общая нерелятивистская тормозная способность представляет собой сумму двух членов: . Было разработано несколько полуэмпирических формул тормозной способности. Модель, предложенная Циглером, Бирсаком и Литтмарком (так называемая «ZBL»-остановка, см. следующую главу), ^{[16] [17],} реализованная в различных версиях кодов TRIM/SRIM , ^[18] используется сегодня чаще всего. ${\displaystyle F(E)=F_{e}(E)+F_{n}(E)}$

Радиационную тормозную способность , которая обусловлена ​​испусканием тормозного излучения в электрических полях частиц в проходимом материале, необходимо учитывать при чрезвычайно высоких энергиях ионов. ^[12] Для электронных снарядов радиационная тормозная способность всегда важна. При высоких энергиях ионов могут также иметь место потери энергии из-за ядерных реакций, но такие процессы обычно не описываются тормозной способностью. ^[12]

Вблизи поверхности твердого материала мишени как ядерное, так и электронное торможение может привести к распылению .

Процесс замедления в твердых телах

Иллюстрация замедления одиночного иона в твердом материале

В начале процесса замедления при высоких энергиях ион замедляется в основном электронным торможением и движется почти по прямой. Когда ион достаточно замедлится, столкновения с ядрами (ядерное торможение) становятся все более и более вероятными, в конечном итоге доминируя над замедлением. Когда атомы твердого тела получают значительные энергии отдачи при ударе иона, они будут удалены из своих положений в решетке и произведут каскад дальнейших столкновений в материале. Эти каскады столкновений являются основной причиной возникновения повреждений при ионной имплантации в металлы и полупроводники.

Когда энергии всех атомов в системе падают ниже пороговой энергии смещения , производство новых повреждений прекращается, и концепция ядерного торможения больше не имеет смысла. Общее количество энергии, переданной ядерными столкновениями атомам в материалах, называется ядерной депонированной энергией.

Вставка на рисунке показывает типичное распределение пробега ионов, осажденных в твердом теле. Показанный здесь случай может быть, например, замедлением иона кремния с энергией 1 МэВ в кремнии. Средний пробег иона с энергией 1 МэВ обычно находится в микрометровом диапазоне.

Отталкивающиймежатомные потенциалы

На очень малых расстояниях между ядрами отталкивающее взаимодействие можно считать по сути кулоновским. На больших расстояниях электронные облака экранируют ядра друг от друга. Таким образом, отталкивающий потенциал можно описать, умножив кулоновское отталкивание между ядрами на экранирующую функцию φ(r/a),

${\displaystyle V(r)={1 \over 4\pi \varepsilon _{0}}{Z_{1}Z_{2}e^{2} \over r}\varphi (r/a)}$

где φ(r/a) → 1 при r → 0. Здесь и — заряды взаимодействующих ядер, а r — расстояние между ними; a — так называемый параметр экранирования. ${\displaystyle Z_{1}}$ ${\displaystyle Z_{2}}$

За эти годы было предложено большое количество различных отталкивающих потенциалов и экранирующих функций, некоторые из которых были определены полуэмпирически, другие — теоретическими расчетами. Часто используемый отталкивающий потенциал — это потенциал, предложенный Циглером, Бирсаком и Литтмарком, так называемый отталкивающий потенциал ZBL. Он был построен путем подгонки универсальной экранирующей функции к теоретически полученным потенциалам, рассчитанным для большого разнообразия пар атомов. ^[16] Параметр и функция экранирования ZBL имеют вид

${\displaystyle a=a_{u}={0.8854a_{0} \over Z_{1}^{0.23}+Z_{2}^{0.23}}}$

и

${\displaystyle \varphi (x)=0.1818e^{-3.2x}+0.5099e^{-0.9423x}+0.2802e^{-0.4029x}+0.02817e^{-0.2016x}}$

где x = r/a _u , а a ₀ — радиус атома Бора = 0,529 Å.

Стандартное отклонение соответствия универсального отталкивающего потенциала ZBL теоретически рассчитанным парно-специфическим потенциалам, которым он соответствует, составляет 18% выше 2 эВ. ^[16] Еще более точные отталкивающие потенциалы можно получить из самосогласованных расчетов полной энергии с использованием теории функционала плотности и приближения локальной плотности (LDA) для электронного обмена и корреляции. ^[19]

Ченнелинг

В кристаллических материалах ион в некоторых случаях может «каналироваться», т. е. фокусироваться в канале между кристаллическими плоскостями, где он почти не испытывает столкновений с ядрами. ^[20] Кроме того, электронная тормозная способность может быть слабее в канале. ^[21] Таким образом, ядерная и электронная тормозная способность зависят не только от типа и плотности материала, но также от его микроскопической структуры и поперечного сечения.

Компьютерное моделирование замедления ионов

Методы компьютерного моделирования для расчета движения ионов в среде разрабатывались с 1960-х годов и в настоящее время являются доминирующим способом теоретической обработки тормозной способности. Основная идея в них заключается в том, чтобы отслеживать движение иона в среде, моделируя столкновения с ядрами в среде. Электронная тормозная способность обычно учитывается как сила трения, замедляющая ион.

Традиционные методы, используемые для расчета пробегов ионов, основаны на приближении бинарных столкновений (BCA). ^[22] В этих методах движение ионов в имплантированном образце рассматривается как последовательность отдельных столкновений между ионом отдачи и атомами в образце. Для каждого отдельного столкновения классический интеграл рассеяния решается путем численного интегрирования.

Параметр удара p в интеграле рассеяния определяется либо из стохастического распределения, либо способом, учитывающим кристаллическую структуру образца. Первый метод подходит только для моделирования имплантации в аморфные материалы, поскольку не учитывает каналирование.

Самая известная программа моделирования BCA — TRIM/SRIM ( аббревиатура от TRansport of Ions in Matter, в более поздних версиях называется Stopping and Range of Ions in Matter), которая основана на электронном торможении и межатомном потенциале ZBL . ^{[16] [18] [23]} Она имеет очень простой в использовании пользовательский интерфейс и имеет параметры по умолчанию для всех ионов во всех материалах вплоть до энергии ионов 1 ГэВ, что сделало ее чрезвычайно популярной. Однако она не учитывает кристаллическую структуру, что серьезно ограничивает ее полезность во многих случаях. Несколько программ BCA преодолевают эту трудность; некоторые из них довольно известны — MARLOWE, ^[24] BCCRYS и crystal-TRIM.

Хотя методы BCA успешно применялись для описания многих физических процессов, у них есть некоторые препятствия для реалистичного описания процесса замедления энергичных ионов. Основное предположение о том, что столкновения являются бинарными, приводит к серьезным проблемам при попытке учесть множественные взаимодействия. Кроме того, при моделировании кристаллических материалов процесс выбора следующего сталкивающегося атома решетки и параметр удара p всегда включают несколько параметров, которые могут не иметь идеально определенных значений, что может повлиять на результаты на 10–20% даже для вполне разумных, на первый взгляд, выборов значений параметров. Наилучшая надежность в BCA достигается путем включения в расчеты множественных столкновений, что нелегко сделать правильно. Однако, по крайней мере, MARLOWE делает это.

Принципиально более простой способ моделирования множественных атомных столкновений обеспечивается моделированием молекулярной динамики (МД), в котором временная эволюция системы атомов рассчитывается путем численного решения уравнений движения. Были разработаны специальные методы МД, в которых число взаимодействий и атомов, участвующих в моделировании МД, было уменьшено, чтобы сделать их достаточно эффективными для расчета пробегов ионов. ^{[25] [26]} Моделирование МД автоматически описывает ядерную тормозную способность. Электронную тормозную способность можно легко включить в моделирование молекулярной динамики либо как силу трения ^{[25] [27] [28] [29] [26] [30] [31] [32]} или более продвинутым способом, также отслеживая нагрев электронных систем и связывая электронные и атомные степени свободы. ^{[33] [34] [35]}

Минимальная ионизирующая частица

За пределами максимума тормозная способность уменьшается примерно как 1/v ² с ростом скорости частицы v , но после минимума она снова увеличивается. ^[36] Минимальная ионизирующая частица (MIP) — это частица, средняя скорость потери энергии которой через вещество близка к минимуму. Во многих практических случаях релятивистские частицы (например, мюоны космических лучей ) являются минимально ионизирующими частицами. Важным свойством всех минимально ионизирующих частиц является то, что приблизительно верно, где и — обычные релятивистские кинематические величины. Более того, все MIP имеют почти одинаковую потерю энергии в веществе, значение которой равно: . ^[36] ${\displaystyle \beta \gamma \simeq 3}$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle -{\frac {dE}{dx}}\simeq 2{\frac {\text{MeV}}{\mathrm {g} \,{\text{cm}}^{-2}}}}$

Смотрите также

• Длина излучения
• Длина затухания
• Каскад столкновений
• Радиационное материаловедение

Ссылки

1. Брэгг, WH (1905). «О α-частицах радия и потере ими пробега при прохождении через различные атомы и молекулы». Phil. Mag . 10 (57): 318. doi :10.1080/14786440509463378.
2. Бор, Н. (1913). «О теории уменьшения скорости движущихся электрифицированных частиц при прохождении через вещество». Phil. Mag . 25 (145): 10. doi :10.1080/14786440108634305.
3. Отчет 73 ICRU: Остановка ионов тяжелее гелия, Журнал ICRU, 5 № 1 (2005), Oxford Univ. Press ISBN 0-19-857012-0 
4. Podgorsak, EB, ред. (2005). Radiation Oncology Physics: A Handbook for Teachers and Students (PDF) . Вена: Международное агентство по атомной энергии. ISBN 978-92-0-107304-4. Получено 25 ноября 2012 г.
5. Международная комиссия по радиационным единицам и измерениям (1970). Линейная передача энергии (PDF) . Вашингтон, округ Колумбия, ISBN 978-0913394090. Отчет ICRU 16 . Получено 1 декабря 2012 г. .{{cite book}}: CS1 maint: location missing publisher (link)
6. Yang, C.; Di Li, Di Li; Geng Wang, Geng Wang; Li Lin, Li Lin; Tasch, AF; Banerjee, S. (2002). "Квантово-механическая модель электронной тормозной способности для ионов в свободном электронном газе". Технология ионной имплантации. 2002. Труды 14-й Международной конференции по . стр. 556–559. doi :10.1109/IIT.2002.1258065. ISBN 0-7803-7155-0. S2CID  117936302.
7. P. Sigmund: Остановка тяжелых ионов. Springer Tracts in Modern Physics Vol. 204 (2004) ISBN 3-540-22273-1 
8. Zeb, M. Ahsan; Kohanoff, J.; Sánchez-Portal, D.; Arnau, A.; Juaristi, JI; Artacho, Emilio (2012-05-31). "Электронная тормозная способность в золоте: роль d -электронов и аномалия H/He". Physical Review Letters . 108 (22): 225504. arXiv : 1205.1728 . Bibcode : 2012PhRvL.108v5504Z. doi : 10.1103/PhysRevLett.108.225504. PMID  23003620. S2CID  2682651.
9. Улла, Рафи; Корсетти, Фабиано; Санчес-Портал, Даниэль; Артачо, Эмилио (2015-03-11). "Электронная тормозная способность в полупроводнике с узкой запрещенной зоной из первых принципов". Physical Review B. 91 ( 12): 125203. arXiv : 1410.6642 . Bibcode : 2015PhRvB..91l5203U. doi : 10.1103/PhysRevB.91.125203. S2CID  31233417.
10. "Остановочная сила для легких ионов". Архивировано из оригинала 2012-02-06 . Получено 2014-02-19 .
11. Пол, Х (2006). «Сравнение последних таблиц тормозной способности для легких и среднетяжелых ионов с экспериментальными данными и приложения к дозиметрии радиотерапии». Ядерные приборы и методы в физических исследованиях B. 247 ( 2): 166–172. Bibcode : 2006NIMPB.247..166P. doi : 10.1016/j.nimb.2006.01.059.
12. Международная комиссия по радиационным единицам и измерениям (октябрь 2011 г.). Seltzer, Stephen M. (ред.). "Fundamental Quantities and Units for Ionizing Radiation" (PDF) . Журнал ICRU . 11 (1) (пересмотренное издание): NP.2–NP. doi :10.1093/jicru/ndr012. PMID  24174259. Отчет ICRU 85a . Получено 14 декабря 2012 г. .^{[ постоянная мертвая ссылка ]}
13. Хухтинен, Мика (2002). «Моделирование неионизирующих потерь энергии и образования дефектов в кремнии». Ядерные приборы и методы в исследованиях физики B. 491 ( 1–2): 194–215. Bibcode : 2002NIMPA.491..194H. doi : 10.1016/s0168-9002(02)01227-5.
14. Barry, AL; Houdayer, AJ; Hinrichsen, PF; Letourneau, WG; Vincent, J (1995). "Энергетическая зависимость констант повреждения в течение срока службы светодиодов на основе GaAs для протонов с энергией 1-500 МэВ". IEEE Transactions on Nuclear Science . 42 (6): 2104–2107. Bibcode : 1995ITNS...42.2104B. doi : 10.1109/23.489259.
15. Линдстрём, Г (2001). «Радиационно-стойкие кремниевые детекторы — разработки коллаборации RD48 (ROSE)». Ядерные приборы и методы в физических исследованиях A. 466 ( 2): 308–326. Bibcode :2001NIMPA.466..308L. doi :10.1016/S0168-9002(01)00560-5. hdl : 11568/67464 .
16. JF Ziegler, JP Biersack и U. Littmark. В The Stopping and Range of Ions in Matter, том 1, Нью-Йорк, 1985. Pergamon. ISBN 0-08-022053-3 
17. JF Ziegler, JP Biersack и MD Ziegler: SRIM - Остановка и пробег ионов в веществе, SRIM Co., 2008. ISBN 0-9654207-1-X 
18. веб-сайт SRIM
19. Нордлунд, К; Рунеберг, Н; Сундхольм, Д (1997). «Отталкивающие межатомные потенциалы, вычисленные с использованием методов теории Хартри-Фока и функционала плотности». Ядерные приборы и методы в исследованиях физики B. 132 ( 1): 45. Bibcode :1997NIMPB.132...45N. doi :10.1016/S0168-583X(97)00447-3.
20. Эйзен, ФХ (1968-03-15). «Каналирование ионов средней массы через кремний». Канадский журнал физики . 46 (6): 561–572. doi :10.1139/p68-070. ISSN  0008-4204.
21. Нтемоу, Элени; Холеньяк, Радек; Приметцхофер, Даниэль (2022-05-01). "Выделение энергии ионами H и He при энергиях кэВ в самоподдерживающихся монокристаллических фольгах SiC". Радиационная физика и химия . 194 : 110033. doi :10.1016/j.radphyschem.2022.110033. ISSN  0969-806X.
22. Робинсон, Марк; Торренс, Ян (1974). «Компьютерное моделирование каскадов атомных смещений в твердых телах в приближении бинарных столкновений». Physical Review B. 9 ( 12): 5008. Bibcode : 1974PhRvB...9.5008R. doi : 10.1103/PhysRevB.9.5008.
23. Бирсак, Дж.; Хаггмарк, Л. (1980). «Компьютерная программа Монте-Карло для переноса энергичных ионов в аморфных мишенях☆». Ядерные приборы и методы . 174 (1): 257. Bibcode : 1980NucIM.174..257B. doi : 10.1016/0029-554X(80)90440-1.
24. Робинсон, М. (1992). «Исследования компьютерного моделирования каскадов столкновений высокой энергии1». Ядерные приборы и методы в исследованиях физики B. 67 ( 1–4): 396–400. Bibcode : 1992NIMPB..67..396R. doi : 10.1016/0168-583X(92)95839-J.
25. Nordlund, K (1995). "Моделирование молекулярной динамики пробегов ионов в диапазоне энергий 1–100 кэВ". Computational Materials Science . 3 (4): 448–456. doi :10.1016/0927-0256(94)00085-Q.
26. Бирдмор, Кейт; Гренбек-Йенсен, Нильс (1998). «Эффективная схема молекулярной динамики для расчета профилей легирующих примесей при ионной имплантации». Physical Review E. 57 ( 6): 7278–7287. arXiv : physics/9901054 . Bibcode : 1998PhRvE..57.7278B. CiteSeerX 10.1.1.285.6727 . doi : 10.1103/PhysRevE.57.7278. S2CID  13994369. 
27. Хоблер, Г. (2001). «О полезной области применения моделирования молекулярной динамики в приближении взаимодействия отдачи». Ядерные приборы и методы в исследованиях физики B. 180 ( 1–4): 203. Bibcode : 2001NIMPB.180..203H. doi : 10.1016/s0168-583x(01)00418-9.
28. Катурла, М. (1996). «Ионно-лучевая обработка кремния при энергиях кэВ: молекулярно-динамическое исследование». Physical Review B. 54 ( 23): 16683–16695. Bibcode : 1996PhRvB..5416683C. doi : 10.1103/PhysRevB.54.16683. PMID  9985796.
29. Смит, Р. (1997). "Моделирование молекулярной динамики бомбардировки Ni {100} ионами с энергией 0,1-2 кэВ". Радиационные эффекты и дефекты в твердых телах . 141 : 425. doi :10.1080/10420159708211586.
30. Duvenbeck, A. (2007). "Продвижение электронов и электронное трение в каскадах атомных столкновений". New Journal of Physics . 9 (2): 38. Bibcode : 2007NJPh....9...38D. doi : 10.1088/1367-2630/9/2/038 .
31. Хоу, М. (2000). «Осаждение кластеров AuN на поверхностях Au(111). I. Моделирование в атомном масштабе». Physical Review B. 62 ( 4): 2825. Bibcode : 2000PhRvB..62.2825H. doi : 10.1103/PhysRevB.62.2825.
32. Bjorkas, C. (2009). "Оценка связи между смешиванием ионного пучка, электрон-фононной связью и образованием повреждений в Fe". Ядерные приборы и методы в исследованиях физики B. 267 ( 10): 1830. Bibcode : 2009NIMPB.267.1830B. doi : 10.1016/j.nimb.2009.03.080.
33. Pronnecke, S. (1991). "Влияние потери электронной энергии на динамику тепловых пиков в Cu" (PDF) . Journal of Materials Research . 6 (3): 483. Bibcode :1991JMatR...6..483P. doi :10.1557/jmr.1991.0483. S2CID  96618269.
34. Даффи, ДМ (2007). «Включая эффекты электронного торможения и электрон-ионных взаимодействий в моделирование радиационного повреждения». Журнал физики: конденсированное вещество . 17 (1): 016207. Bibcode : 2007JPCM...19a6207D. doi : 10.1088/0953-8984/19/1/016207. S2CID  122777435.
35. Тамм, А. (2016). «Взаимодействие электронов и фононов в рамках классической молекулярной динамики». Physical Review B. 94 ( 1): 024305. Bibcode : 2016PhRvB..94a4305L. doi : 10.1103/PhysRevB.94.014305.
36. http://pdg.lbl.gov/2005/reviews/passagerpp.pdf ^{[ пустой URL-адрес PDF ]}

Дальнейшее чтение

• (Линдхард, 1963) Дж. Линдхард, М. Шарфф и Х. Е. Шьотт. Концепции дальности и дальности тяжелых ионов. Мат. Фис. Медд. Дэн. Вид. Сельск., 33(14):1, 1963.
• (Смит, 1997) Р. Смит (ред.), Атомные и ионные столкновения в твердых телах и на поверхностях: теория, моделирование и приложения, Cambridge University Press, Кембридж, Великобритания, 1997.

Внешние ссылки

• Расчеты тормозной способности и потери энергии в твердых телах с помощью модели MELF-GOS Архивировано 25.09.2010 на Wayback Machine
• Веб-модуль для дальности и останавливающей силы в Nucleonica
• Прохождение заряженных частиц через вещество
• Таблицы тормозной способности и пробега для электронов, протонов и ионов гелия
• Тормозная способность: графики и данные
• Проникновение заряженных частиц через вещество; конспект лекций Э. Бондерупа