Вычитание

Одна из четырех основных арифметических операций.

« 5 − 2 = 3» (устно «пять минус два равно трем»)

Плакат возле магазина в Бордо , рекламирующий вычет 20% от цены второго купленного парфюма.

Вычитание (обозначаемое знаком минус – ) является одной из четырёх арифметических операций наряду со сложением , умножением и делением . Вычитание — это операция, представляющая собой удаление объектов из коллекции. ^[1] Например, на соседнем рисунке 5–2 персика — то есть 5 персиков, из которых 2 убраны, в результате чего получается 3 персика. Следовательно, разница 5 и 2 равна 3; то есть 5 - 2 = 3 . Хотя вычитание в первую очередь связано с натуральными числами в арифметике , оно также может представлять собой удаление или уменьшение физических и абстрактных величин с использованием различных типов объектов, включая отрицательные числа , дроби , иррациональные числа , векторы , десятичные дроби, функции и матрицы. ^[2]

В некотором смысле вычитание является обратным действием сложения. То есть c = a − b тогда и только тогда, когда c + b = a . Прописью: разность двух чисел — это число, которое дает первое при сложении со вторым.

Вычитание следует нескольким важным закономерностям. Он антикоммутативен , то есть изменение порядка меняет знак ответа. Оно также не является ассоциативным , что означает, что при вычитании более двух чисел порядок выполнения вычитания имеет значение. Поскольку — это аддитивная единица , ее вычитание не меняет числа. Вычитание также подчиняется предсказуемым правилам, касающимся связанных операций, таких как сложение и умножение . Все эти правила можно доказать , начиная с вычитания целых чисел и обобщения действительных чисел и далее. Общие бинарные операции , которые следуют этим шаблонам, изучаются в абстрактной алгебре .

В теории вычислимости , учитывая, что вычитание не является четко определенным над натуральными числами , операции между числами фактически определяются с использованием «усеченного вычитания» или монуса . ^[3]

Обозначения и терминология

Вычитание чисел 0–10. Метки строк = уменьшаемые. Ось X = вычитаемое. Ось Y = разница.

Вычитание обычно записывается со знаком минус «-» между членами; то есть в инфиксной записи . Результат выражается знаком равенства . Например,

${\displaystyle 2-1=1}$(произносится как «два минус один равно одному»)

${\displaystyle 4-2=2}$(произносится как «четыре минус два равно два»)

${\displaystyle 6-3=3}$(произносится как «шесть минус три равно три»)

${\displaystyle 4-6=-2}$(произносится как «четыре минус шесть равно минус два»)

Бывают также ситуации, когда вычитание «понятно», даже если символ ^{не появляется :}

• Столбец из двух чисел, где меньшее число выделено красным, обычно означает, что нужно вычесть меньшее число в столбце, а разница указана ниже, под чертой. Это наиболее распространено в бухгалтерском учете.

Формально вычитаемое число называется вычитаемым , [ ^{4] [5],} а число, из которого оно вычитается, — вычитаемым . ^{[4] [5]} Результат — это разница . ^{[4] [5] [2] [6]} То есть,

${\displaystyle {\rm {minuend}}-{\rm {subtrahend}}={\rm {difference}}}$.

Вся эта терминология происходит от латыни . «Вычитание» — английское слово, происходящее от латинского глагола subtrahere , который, в свою очередь, представляет собой соединение слов sub «из-под» и trahere «тянуть». Таким образом, вычитать — значит рисовать снизу или отнимать . ^[7] Использование суффикса герундия -nd приводит к «вычитанию», «вещи, которую нужно вычесть». ^[а] Точно так же от minuere «уменьшать или уменьшать» получается «minuend», что означает «вещь, которую нужно уменьшить».

О целых и действительных числах

Целые числа

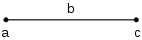
Представьте себе отрезок длины b с левым концом, обозначенным a, и правым концом, обозначенным c . Начиная с a , нужно сделать b шагов вправо, чтобы достичь c . Это движение вправо моделируется математически сложением :

а + б = с .

Из c нужно сделать b шагов влево , чтобы вернуться в a . Это движение влево моделируется вычитанием:

с - б знак равно а .

Теперь отрезок прямой, помеченный цифрами 1 , 2 и 3 . Из позиции 3 не нужно делать никаких шагов влево, чтобы остаться в позиции 3, поэтому 3 − 0 = 3 . Чтобы добраться до позиции 1, нужно сделать 2 шага влево, поэтому 3 − 2 = 1 . Эта картина недостаточна для описания того, что произойдет после прохождения трех шагов влево от позиции 3. Чтобы представить такую ​​операцию, линию необходимо продлить.

Чтобы вычесть произвольные натуральные числа , нужно начать со строки, содержащей все натуральные числа (0, 1, 2, 3, 4, 5, 6, ...). От 3 требуется 3 шага влево, чтобы добраться до 0, поэтому 3 − 3 = 0 . Но 3−4 всё равно недействительно, так как снова выходит за пределы строки. Натуральные числа не являются полезным контекстом для вычитания.

Решение состоит в том, чтобы рассмотреть строку целых чисел (..., −3, −2, −1, 0, 1, 2, 3, ...). Таким образом, чтобы добраться до −1, потребуется сделать 4 шага влево от 3:

3 - 4 = -1 .

Натуральные числа

Вычитание натуральных чисел не является закрытым : разность не является натуральным числом, если вычитаемое не больше или равно вычитаемому. Например, из 11 нельзя вычесть 26, чтобы получить натуральное число. В таком случае используется один из двух подходов:

1. Сделайте вывод, что 26 нельзя вычесть из 11; вычитание становится частичной функцией .
2. Ответ дайте в виде целого числа , представляющего отрицательное число , поэтому результат вычитания 26 из 11 равен −15.

Вещественные числа

Поле действительных чисел можно определить, указав только две двоичные операции: сложение и умножение, а также унарные операции , дающие аддитивные и мультипликативные обратные операции. Вычитание одного действительного числа (вычитаемого) из другого (вычитаемого) можно тогда определить как сложение уменьшаемого и аддитивного обратного вычитаемого числа. Например, 3 − π = 3 + (− π ) . Альтернативно, вместо того, чтобы требовать этих унарных операций, в качестве базовых можно взять бинарные операции вычитания и деления .

Характеристики

Антикоммутативность

Вычитание является антикоммутативным , что означает, что если поменять местами члены разности слева направо, результат будет отрицательным по сравнению с исходным результатом. Символически, если a и b — любые два числа, то

а - б знак равно -( б - а) .

Неассоциативность

Вычитание неассоциативно , что возникает, когда кто-то пытается определить повторяющееся вычитание. В целом выражение

" а - б - с "

можно определить как ( a − b ) − c или a − ( b − c ), но эти две возможности приводят к разным ответам. Чтобы решить эту проблему, необходимо установить порядок операций , при котором разные порядки дают разные результаты.

Предшественник

В контексте целых чисел вычитание единицы также играет особую роль: для любого целого числа a целое число ( a − 1) является наибольшим целым числом, меньшим, чем a , также известным как предшественник a .

Меры измерения

При вычитании двух чисел с единицами измерения, такими как килограммы или фунты , они должны иметь одну и ту же единицу измерения. В большинстве случаев разница будет иметь ту же единицу измерения, что и исходные числа.

Проценты

Об изменениях в процентах можно сообщать как минимум в двух формах: процентном изменении и изменении в процентных пунктах . Процентное изменение представляет собой относительное изменение между двумя величинами в процентах, тогда как изменение в процентном пункте — это просто число, полученное путем вычитания двух процентов. ^{[8] [9] [10]}

В качестве примера предположим, что 30% изделий, изготовленных на заводе, бракованы. Спустя полгода 20% виджетов оказались бракованными. Процентное изменение составляет20% − 30%/30%= −1/3= −33+1/3%, а изменение процентных пунктов составляет −10 процентных пунктов.

В вычислительной технике

Метод дополнений — это метод, используемый для вычитания одного числа из другого, используя только сложение положительных чисел. Этот метод обычно использовался в механических калькуляторах и до сих пор используется в современных компьютерах .

Чтобы вычесть двоичное число y (вычитаемое) из другого числа x (вычитаемое), к x добавляется дополнение до единиц y , а к сумме добавляется единица. Затем первая цифра «1» результата отбрасывается.

Метод дополнений особенно полезен в двоичных числах (основание 2), поскольку дополнение до единиц очень легко получить путем инвертирования каждого бита (замены «0» на «1» и наоборот). А добавление 1 для получения дополнения до двух можно выполнить путем имитации переноса в младший бит. Например:

 01100100 (x, равно десятичному 100)- 00010110 (y, равно десятичному 22)

становится суммой:

 01100100 (х)+ 11101001 (дополнение к единице y)+ 1 (чтобы получить дополнение до двух)—————————— 101001110

Удаление начальной «1» дает ответ: 01001110 (равно десятичному 78).

Преподавание вычитания в школах

Методы обучения вычитанию в начальной школе различаются от страны к стране, и внутри страны в разное время применяются разные методы. В том, что известно в Соединенных Штатах как традиционная математика , в конце 1-го курса (или в течение 2-го года) студентам преподают определенный процесс для использования с многозначными целыми числами, который расширяется либо на четвертом, либо на четвертом курсе. В пятом классе включить десятичные представления дробных чисел.

В Америке

Практически во всех американских школах сейчас преподают метод вычитания с использованием заимствования или перегруппировки (алгоритм декомпозиции) и систему разметки, называемую костылями. ^{[11] [12]} Хотя метод заимствования был известен и опубликован в учебниках ранее, использование костылей в американских школах распространилось после того, как Уильям А. Браунелл опубликовал исследование, в котором утверждалось, что костыли были полезны для учащихся, использующих этот метод. ^[13] Эта система быстро завоевала популярность, вытеснив другие методы вычитания, использовавшиеся в то время в Америке.

В Европе

Некоторые европейские школы используют метод вычитания, называемый австрийским методом, также известный как метод сложения. В этом методе нет заимствований. Есть также костыли (маркировки для улучшения памяти), которые различаются в зависимости от страны. ^{[14] [15]}

Сравнение двух основных методов

Оба эти метода разбивают вычитание на процесс вычитания одной цифры по разряду. Вычитание вычитаемого, начиная с младшей значащей цифры:

s _j s _{j −1} ... s ₁

из минуса

м _k м _{k −1} ... м ₁ ,

где каждый s _i и m _i является цифрой, продолжается записью m ₁ - s ₁ , m ₂ - s ₂ и т. д. до тех пор, пока s _i не превышает m _i . В противном случае m _i увеличивается на 10, и какая-то другая цифра изменяется, чтобы исправить это увеличение. Американский метод корректирует, пытаясь уменьшить уменьшаемую цифру m _{i +1} на единицу (или продолжая заимствование влево до тех пор, пока не появится ненулевая цифра, из которой можно заимствовать). Европейский метод исправляет, увеличивая вычитаемую цифру s _{i +1} на единицу.

Пример: 704–512.

${\displaystyle {\begin{array}{rrrr}&\color {Red}-1\\&C&D&U\\&7&0&4\\&5&1&2\\\hline &1&9&2\\\end{array}}{\begin{array}{l}{\color {Red}\longleftarrow {\rm {carry}}}\\\\\longleftarrow \;{\rm {Minuend}}\\\longleftarrow \;{\rm {Subtrahend}}\\\longleftarrow {\rm {Rest\;or\;Difference}}\\\end{array}}}$

Сокращаемое — 704, вычитаемое — 512. Сокращаемые цифры — m ₃ = 7 , m ₂ = 0 и m ₁ = 4 . Вычитаемые цифры: s ₃ = 5 , s ₂ = 1 и s ₁ = 2 . Начиная с единицы, 4 не меньше 2, поэтому разница 2 записывается на месте единицы результата. В разряде десятков 0 меньше 1, поэтому 0 увеличивается на 10, а разница с 1, равная 9, записывается в разряде десятков. Американский метод корректирует увеличение десяти путем уменьшения цифры в разряде сотен на единицу. То есть 7 зачеркивается и заменяется 6. Затем вычитание продолжается в разряде сотен, где 6 не меньше 5, поэтому разница записывается в разряде сотен результата. Мы закончили, результат — 192.

Австрийский метод не уменьшает 7 до 6, а увеличивает вычитаемую цифру сотен на единицу. Рядом с этой цифрой или под ней делается небольшая отметка (в зависимости от школы). Затем вычитание продолжается, когда задается вопрос, какое число, увеличенное на 1 и добавленное к нему 5, дает 7. Ответ — 1, и он записывается в разряде сотен результата.

Есть еще одна тонкость: в американском методе ученик всегда пользуется мысленной таблицей вычитания. Австрийский метод часто побуждает ученика мысленно использовать таблицу сложения в обратном порядке. В приведенном выше примере вместо того, чтобы прибавлять 1 к 5, получать 6 и вычитать это из 7, ученика просят подумать, какое число, увеличенное на 1 и добавленное к нему 5, дает 7.

Вычитание вручную

Австрийский метод

Пример: ^{[ нужна ссылка ]}

• 
  1 + ... = 3
• 
  Разница написана под чертой.
• 
  9 + ... = 5
  Искомая сумма (5) слишком мала.
• 
  Итак, прибавляем к нему 10 и ставим 1 под следующим по величине местом в вычитаемом.
• 
  9 + ... = 15
  Теперь мы можем найти разницу, как и раньше.
• 
  (4 + 1) + ... = 7
• 
  Разница написана под чертой.
• 
  Общая разница.

Вычитание слева направо

Пример: ^{[ нужна ссылка ]}

• 
  7 − 4 = 3
  Этот результат лишь зачеркнут карандашом.
• 
  Поскольку следующая цифра уменьшаемого меньше вычитаемого, мы вычитаем единицу из числа, записанного карандашом, и мысленно прибавляем десять к следующей цифре.
• 
  15 − 9 = 6
• 
  Поскольку следующая цифра в уменьшаемом не меньше вычитаемого, мы сохраняем это число.
• 
  3 - 1 = 2

Американский метод

В этом методе каждая цифра вычитаемого вычитается из цифры над ней, начиная справа налево. Если верхнее число слишком мало, чтобы из него можно было вычесть нижнее, прибавляем к нему 10; эта 10 «позаимствована» у верхней цифры слева, из которой мы вычитаем 1. Затем мы переходим к вычитанию следующей цифры и заимствованию по мере необходимости, пока не будет вычтена каждая цифра. Пример: ^{[ нужна ссылка ]}

• 
  3 − 1 = ...
• 
  Пишем разницу под чертой.
• 
  5 − 9 = ...
  Исключаемое (5) слишком мало!
• 
  Итак, прибавляем к нему 10. 10 «заимствована» у цифры слева, которая уменьшается на 1.
• 
  15 − 9 = ...
  Теперь вычитание работает, и разницу пишем под чертой.
• 
  6 − 4 = ...
• 
  Пишем разницу под чертой.
• 
  Общая разница.

Сначала торгуйте

Вариант американского метода, в котором все заимствования выполняются перед вычитанием. ^[16]

Пример:

• 
  1–3 = невозможно.
  К 1 добавляем 10. Поскольку 10 «заимствована» у соседних 5, 5 понижается на 1.
• 
  4–9 = невозможно.
  Итак, действуем, как в пункте 1.
• 
  Работаем справа налево:
  11 − 3 = 8.
• 
  14 − 9 = 5
• 
  6 − 4 = 2

Частичные различия

Метод частичных разностей отличается от других методов вертикального вычитания тем, что не происходит заимствования или переноса. Вместо них ставятся знаки плюс или минус в зависимости от того, больше или меньше вычитаемое вычитаемое. Сумма частных разностей равна общей разнице. ^[17]

Пример:

• 
  Меньшее число вычитается из большего:
  700 − 400 = 300.
  Поскольку уменьшаемое больше вычитаемого, эта разность имеет знак плюс.
• 
  Меньшее число вычитается из большего:
  90 − 50 = 40.
  Поскольку уменьшаемое меньше вычитаемого, эта разность имеет знак минус.
• 
  Меньшее число вычитается из большего:
  3 − 1 = 2.
  Поскольку уменьшаемое больше вычитаемого, эта разность имеет знак плюс.
• 
  +300 − 40 + 2 = 262

Невертикальные методы

Подсчет

Вместо того, чтобы находить разницу по цифрам, можно подсчитать числа между вычитаемым и вычитаемым. ^[18]

Пример: 1234 − 567 = можно найти, выполнив следующие действия:

• 567 + 3 = 570
• 570 + 30 = 600
• 600 + 400 = 1000
• 1000 + 234 = 1234

Сложите значения каждого шага, чтобы получить общую разницу: 3 + 30 + 400 + 234 = 667 .

Разрыв вычитания

Другой метод, полезный для ментальной арифметики , — разбить вычитание на небольшие этапы. ^[19]

Пример: 1234 − 567 = можно решить следующим образом:

• 1234 − 500 = 734
• 734 − 60 = 674
• 674 − 7 = 667

То же изменение

Тот же метод изменения использует тот факт, что добавление или вычитание одного и того же числа из уменьшаемого и вычитаемого не меняет ответ. Просто прибавляется сумма, необходимая для получения нулей в вычитаемом. ^[20]

Пример:

«1234 − 567 =" можно решить следующим образом:

• 1234–567 = 1237–570 = 1267–600 = 667

Смотрите также

• Абсолютная разница
• Декремент
• Элементарная арифметика
• Метод дополнений
• Отрицательное число
• Знаки плюс и минус
• Монус (усеченное вычитание)

Примечания

1. «Вычитаемое» сокращается за счет флективного латинского суффикса -us, например, остается несклоняемым, как в numerus subtrahendus «число, которое нужно вычесть».

Рекомендации

1. «Что такое вычесть?». ВсплескУзнайте . 28 апреля 2022 г. Проверено 13 декабря 2022 г.
2. Вайсштейн, Эрик В. «Вычитание». mathworld.wolfram.com . Проверено 26 августа 2020 г.
3. Катленд, Найджел. Вычислимость: введение в рекурсивную теорию функций .
4. Шмид, Герман (1974). Десятичные вычисления (1-е изд.). Бингемтон, Нью-Йорк: John Wiley & Sons . ISBN 978-0-471-76180-8.
5. Шмид, Герман (1983) [1974]. Десятичные вычисления (1 (переиздание) изд.). Малабар, Флорида: Издательство Роберта Э. Кригера. ISBN 978-0-89874-318-0.
6. «Вычитание». www.mathsisfun.com . Проверено 26 августа 2020 г.
7. «Вычитание» . Оксфордский словарь английского языка (онлайн-изд.). Издательство Оксфордского университета . (Требуется подписка или членство участвующей организации.)
8. Пол Э. Петерсон, Майкл Хендерсон, Мартин Р. Уэст (2014) Учителя против общественности: что американцы думают о школах и как их исправить Brookings Institution Press, стр. 163
9. Джанет Колодзи (2006) Конвергентная журналистика: написание и репортажи в средствах массовой информации Rowman & Littlefield Publishers, стр. 180
10. Дэвид Гиллборн (2008) Расизм и образование: совпадение или заговор? Рутледж с. 46
11. Клэппер, Пол (1916). Обучение арифметике: Пособие для учителей. стр. 80– . Проверено 11 марта 2016 г.
12. Сьюзен Росс и Мэри Пратт-Коттер. 2000. «Вычитание в Соединенных Штатах: историческая перспектива», Учитель математики 8 (1): 4–11. п. 8: «Эта новая версия алгоритма декомпозиции [т.е. с использованием костыля Браунелла] настолько доминировала в этой области, что сегодня [в Америке] редко можно увидеть какой-либо другой алгоритм, используемый для обучения вычитанию».
13. Росс, Сьюзен С.; Пратт-Коттер, Мэри (1999). «Вычитание с исторической точки зрения». Школьная наука и математика . 99 (7): 389–93. doi :10.1111/j.1949-8594.1999.tb17499.x.
14. Клэппер 1916, стр. 177–.
15. Дэвид Юджин Смит (1913). Преподавание арифметики. Джинн. стр. 77– . Проверено 11 марта 2016 г.
16. Множество способов арифметики в повседневной математике UCSMP. Архивировано 25 февраля 2014 г. на сайте Wayback Machine Subtraction: Trade First.
17. Вычитание частичных разностей. Архивировано 23 июня 2014 г. в Wayback Machine ; Множество способов арифметики в повседневной математике UCSMP. Архивировано 25 февраля 2014 г. на сайте Wayback Machine. Вычитание: частичные разности.
18. Множество способов арифметики в повседневной математике UCSMP. Архивировано 25 февраля 2014 г. на сайте Wayback Machine Subtraction: Counting Up.
19. Многие способы арифметики в повседневной математике UCSMP. Архивировано 25 февраля 2014 г. на сайте Wayback Machine Subtraction: вычитание слева направо.
20. Множество способов арифметики в вычитании повседневной математики UCSMP: одно и то же правило изменения

Библиография

• Браунелл, Вашингтон (1939). Обучение как реорганизация: экспериментальное исследование по арифметике для третьего класса, Duke University Press.
• Вычитание в Соединенных Штатах: историческая перспектива, Сьюзан Росс, Мэри Пратт-Коттер, Учитель математики, Vol. 8, № 1 (оригинальная публикация) и Том. 10, № 1 (репринт.) PDF

Внешние ссылки

• «Вычитание», Математическая энциклопедия , EMS Press , 2001 [1994]
• Рабочие листы для печати: рабочие листы вычитания, вычитание одной цифры, вычитание двух цифр, вычитание четырех цифр и другие рабочие листы вычитания
• Игра на вычитание
• Вычитание на японских счетах, выбранных из книги «Счеты: тайна бусины».