stringtranslate.com

орбита Земли

Земля в сезонных точках своей орбиты (не в масштабе)
Орбита Земли (желтая) в сравнении с окружностью (серая)

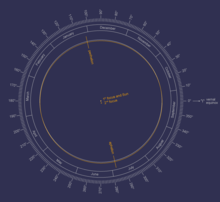
Земля вращается вокруг Солнца на среднем расстоянии 149,60 млн км (92,96 млн миль) или 8,317 световых минут [1] против часовой стрелки , если смотреть сверху на Северное полушарие . Один полный оборот занимает 365,256  дней (1 сидерический год ), за это время Земля проходит 940 млн км (584 млн миль). [2] Игнорируя влияние других тел Солнечной системы , орбита Земли , также называемая вращением Земли , представляет собой эллипс с барицентром Земля-Солнце в качестве одного из фокусов с текущим эксцентриситетом 0,0167. Поскольку это значение близко к нулю, центр орбиты находится относительно близко к центру Солнца (относительно размера орбиты).

При наблюдении с Земли, орбитальное прямолинейное движение планеты заставляет Солнце двигаться относительно других звезд со скоростью около 1° к востоку за солнечные сутки (или диаметр Солнца или Луны за 12 часов). [nb 1] Средняя скорость движения Земли по орбите составляет 29,78 км/с (19 миль/с; 107 208 км/ч; 66 616 миль/ч), что достаточно быстро, чтобы покрыть диаметр планеты за 7 минут и расстояние до Луны за 4 часа. [3]

С точки зрения, находящейся над северным полюсом Солнца или Земли, Земля будет казаться вращающейся против часовой стрелки вокруг Солнца. С той же точки зрения, и Земля, и Солнце будут казаться вращающимися также против часовой стрелки вокруг своих соответствующих осей.

История изучения

Гелиоцентрическая Солнечная система
Гелиоцентризм (нижняя панель) в сравнении с геоцентрической моделью (верхняя панель), не в масштабе

Гелиоцентризм — это научная модель, которая впервые поместила Солнце в центр Солнечной системы и поместила планеты, включая Землю, на его орбиту. Исторически гелиоцентризм противостоит геоцентризму , который поместил Землю в центр. Аристарх Самосский уже предложил гелиоцентрическую модель в третьем веке до нашей эры. В шестнадцатом веке Николай Коперник в своей работе «О вращении небесных сфер» представил полное обсуждение гелиоцентрической модели Вселенной [4] во многом таким же образом, как Птолемей представил свою геоцентрическую модель во втором веке. Эта « коперниканская революция » решила вопрос о планетарном ретроградном движении , утверждая, что такое движение было только воспринимаемым и кажущимся. По словам историка Джерри Броттона , «хотя новаторская книга Коперника... была [напечатана более] столетием ранее, [голландский картограф] Джоан Блау был первым картографом, который включил свою революционную гелиоцентрическую теорию в карту мира». [5]

Влияние на Землю

Из-за наклона оси Земли (часто называемого наклоном эклиптики ) , наклон траектории Солнца в небе (как видно наблюдателю на поверхности Земли) меняется в течение года. Для наблюдателя в северной широте, когда северный полюс наклонен к Солнцу, день длится дольше, и Солнце кажется выше в небе. Это приводит к более высоким средним температурам, так как дополнительная солнечная радиация достигает поверхности. Когда северный полюс наклонен от Солнца, происходит обратное, и погода, как правило, прохладнее. К северу от Полярного круга и к югу от Полярного круга достигается экстремальный случай, при котором в течение части года вообще нет дневного света, а в противоположное время года непрерывный дневной свет. Это называется полярной ночью и полуночным солнцем соответственно. Это изменение погоды (из-за направления наклона оси Земли) приводит к смене времен года . [6]

События на орбите

Согласно астрономической традиции, четыре сезона определяются солнцестояниями ( двумя точками на орбите Земли, в которых ось Земли максимально наклонена к Солнцу или от Солнца) и равноденствиями (двумя точками на орбите Земли, в которых наклоненная ось Земли и воображаемая линия, проведенная от Земли к Солнцу, точно перпендикулярны друг другу). Солнцестояния и равноденствия делят год на четыре приблизительно равные части. В северном полушарии зимнее солнцестояние происходит около 21 декабря; летнее солнцестояние около 21 июня; Весеннее равноденствие приходится примерно на 20 марта, а осеннее равноденствие — примерно на 23 сентября. [7] Влияние наклона земной оси в южном полушарии противоположно в северном полушарии, поэтому сезоны солнцестояний и равноденствий в южном полушарии обратны таковым в северном полушарии (например, летнее солнцестояние в северном полушарии совпадает с зимним солнцестоянием в южном полушарии).

В наше время перигелий Земли происходит около 3 января, а афелий около 4 июля. Другими словами, Земля ближе к Солнцу в январе и дальше в июле, что может показаться нелогичным для тех, кто проживает в северном полушарии, где холоднее, когда Земля находится ближе всего к Солнцу, и теплее, когда она дальше всего. Изменение расстояния между Землей и Солнцем приводит к увеличению примерно на 7% общей солнечной энергии, достигающей Земли в перигелии относительно афелия. [8] Поскольку южное полушарие наклонено к Солнцу примерно в то же время, когда Земля достигает наибольшего сближения с Солнцем, южное полушарие получает немного больше энергии от Солнца, чем северное в течение года. Однако этот эффект гораздо менее значителен, чем общее изменение энергии из-за осевого наклона, и большая часть избыточной энергии поглощается большей долей поверхности, покрытой водой в южном полушарии. [9]

Сфера Хилла ( гравитационная сфера влияния) Земли имеет радиус около 1 500 000 километров (0,01 а.е. ), что примерно в четыре раза больше среднего расстояния до Луны. [10] [nb 2] Это максимальное расстояние, на котором гравитационное влияние Земли сильнее, чем более удаленных Солнца и планет. Объекты, вращающиеся вокруг Земли, должны находиться в пределах этого радиуса, в противном случае они могут стать несвязанными гравитационным возмущением Солнца.

Следующая диаграмма иллюстрирует положения и взаимосвязь между линиями солнцестояний, равноденствий и апсид эллиптической орбиты Земли. Шесть изображений Земли являются положениями вдоль орбитального эллипса, которые последовательно являются перигелием (периапсисом — ближайшей точкой к Солнцу) в любое время с 2 по 5 января, точкой мартовского равноденствия 19, 20 или 21 марта, точкой июньского солнцестояния 20, 21 или 22 июня, афелием (апоапсисом — самой дальней точкой от Солнца) в любое время с 3 по 5 июля, сентябрьским равноденствием 22, 23 или 24 сентября и декабрьским солнцестоянием 21, 22 или 23 декабря. [7]

Преувеличенная иллюстрация эллиптической орбиты Земли вокруг Солнца, показывающая, что крайние точки орбиты ( апоцентр и перицентр ) не совпадают с четырьмя сезонными крайними точками ( равноденствие и солнцестояние ).
Ориентация движения Земли, Луны и Солнца

Будущее

Математики и астрономы (такие как Лаплас , Лагранж , Гаусс , Пуанкаре , Колмогоров , Владимир Арнольд и Юрген Мозер ) искали доказательства стабильности планетарных движений, и эти поиски привели ко многим математическим разработкам и нескольким последовательным «доказательствам» стабильности Солнечной системы. [14] Согласно большинству прогнозов, орбита Земли будет относительно стабильной в течение длительных периодов. [15]

В 1989 году работа Жака Ласкара показала, что орбита Земли (а также орбиты всех внутренних планет) может стать хаотичной и что ошибка в 15 метров при измерении начального положения Земли сегодня сделает невозможным предсказать, где Земля будет находиться на своей орбите всего через 100 миллионов лет. [16] Моделирование Солнечной системы является предметом, охватываемым задачей n-тел .

Смотрите также

Примечания

  1. ^ Нашей планете требуется около 365 дней, чтобы сделать оборот вокруг Солнца. Полный оборот составляет 360°. Этот факт показывает, что каждый день Земля проходит примерно 1° по своей орбите. Таким образом, будет казаться, что Солнце движется по небу относительно звезд на такую ​​же величину.
  2. ^ Для Земли радиус Хилла равен
    где m — масса Земли, a — астрономическая единица, а M — масса Солнца. Таким образом, радиус в а.е. составляет около . [ необходима цитата ]
  3. ^ Все астрономические величины изменяются как вековые , так и периодически . Приведенные величины являются значениями на момент J2000.0 векового изменения, игнорируя все периодические изменения.
  4. ^ ab афелий = a × (1 + e ); перигелий = a × (1 – e ), где a — большая полуось, а e — эксцентриситет.
  5. ^ В справочнике указана долгота перигелия , которая является суммой долготы восходящего узла и аргумента перигелия. Вычитая из этого (102,937°), долгота узла 174,873° дает −71,936°. Добавление 360° дает 288,064°. Это добавление не изменяет угол, но выражает его в обычном диапазоне 0–360° для долгот.

Ссылки

  1. ^ "Sun: Facts & Figures". Исследование Солнечной системы . Национальное управление по аэронавтике и исследованию космического пространства . Архивировано из оригинала 3 июля 2015 г. Получено 29 июля 2015 г.
  2. ^ Джин Миус , Астрономические алгоритмы , 2-е изд., ISBN 0-943396-61-1 (Ричмонд, Вирджиния: Willmann-Bell, 1998) 238. См. Ellipse#Circumference . Формула Рамануджана достаточно точна. [ нужна ссылка ] 
  3. ^ abcd Уильямс, Дэвид Р. (1 сентября 2004 г.). "Earth Fact Sheet". NASA . Получено 17 марта 2007 г. .
  4. ^ De Revolutionibus Orbium Coelestium . Йоханнес Петрейус. 1543.
  5. ^ Джерри Броттон , История мира в двенадцати картах , Лондон: Allen Lane, 2012, ISBN 9781846140990 стр. 262. 
  6. ^ "Что вызывает смену времён года? (НАСА)" . Получено 22 января 2015 г.
  7. ^ ab "Дата и время солнцестояний и равноденствий". 28 августа 2013 г. Получено 22 января 2015 г.
  8. ^ "Солнечная энергия достигает поверхности Земли". ITACA. Архивировано из оригинала 30 января 2022 года . Получено 30 января 2022 года .{{cite web}}: CS1 maint: бот: исходный статус URL неизвестен ( ссылка )
  9. ↑ Уильямс, Джек (20 декабря 2005 г.). «Наклон Земли создает времена года». USAToday . Получено 17 марта 2007 г.
  10. ^ Васкес, М.; Монтаньес Родригес, П.; Палле, Э. (2006). «Земля как объект астрофизического интереса в поисках внесолнечных планет» (PDF) . Канарский институт астрофизики . Проверено 21 марта 2007 г.
  11. ^ abcde Simon, JL; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (февраль 1994 г.). «Численные выражения для формул прецессии и средних элементов для Луны и планет». Астрономия и астрофизика . 282 (2): 663–683. Bibcode : 1994A&A...282..663S.
  12. ^ Аллен, Клэбон Уолтер; Кокс, Артур Н. (2000). Астрофизические величины Аллена. Springer. стр. 294. ISBN 0-387-98746-0.
  13. ^ Рисунок появляется в нескольких ссылках и получен из элементов VSOP87 из раздела 5.8.3, стр. 675 следующих работ: Simon, JL; Bretagnon, P.; Chapront, J.; Chapront-Touzé, M.; Francou, G.; Laskar, J. (февраль 1994 г.). "Численные выражения для формул прецессии и средние элементы для Луны и планет". Astronomy and Astrophysics . 282 (2): 663–683. Bibcode :1994A&A...282..663S.
  14. ^ Ласкар, Дж. (2001). «Солнечная система: устойчивость». В Мурдин, Пол (ред.). Энциклопедия астрономии и астрофизики . Бристоль: Издательство Института физики . статья 2198.
  15. ^ Гриббин, Джон (2004). Глубокая простота: привнесение порядка в хаос и сложность (1-е американское издание). Нью-Йорк: Random House . ISBN 978-1-4000-6256-0.
  16. ^ "Возможно столкновение Земли и Венеры". 11 июня 2009 г. Архивировано из оригинала 23 января 2015 г. Получено 22 января 2015 г.

Внешние ссылки

На Викискладе есть медиафайлы по теме «Орбита Земли» .