Семиугольник

Форма с семью сторонами

В геометрии семиугольник или гептагон — это семиугольник или многоугольник с семью сторонами.

Семиугольник иногда называют семиугольником , используя «sept-» ( от латинского числового префикса septua-, а не греческого числового префикса hepta- ; оба слова родственные ) вместе с греческим суффиксом «-agon», означающим угол .

Правильный семиугольник

Правильный семиугольник , у которого все стороны и все углы равны, имеет внутренние углы 5π/7 радиан ( 128 4 ⁄ 7 градусов ). Его символ Шлефли — {7}.

Область

Площадь ( A ) правильного семиугольника со стороной длиной a определяется по формуле:

${\displaystyle A={\frac {7}{4}}a^{2}\cot {\frac {\pi }{7}}\simeq 3.634a^{2}.}$

Это можно увидеть, разделив единичный семиугольник на семь треугольных «кусочков пирога» с вершинами в центре и в вершинах семиугольника, а затем разделив пополам каждый треугольник, используя апофему как общую сторону. Апофема — это половина котангенса , а площадь каждого из 14 маленьких треугольников — одна четвертая апофемы. ${\displaystyle \pi /7,}$

Площадь правильного семиугольника, вписанного в окружность радиусом R, равна , а площадь самой окружности равна, таким образом, правильный семиугольник заполняет приблизительно 0,8710 описанной вокруг него окружности. ${\displaystyle {\tfrac {7R^{2}}{2}}\sin {\tfrac {2\pi }{7}},}$ ${\displaystyle \pi R^{2};}$

Строительство

Так как 7 является простым числом Пьерпонта , но не простым числом Ферма , правильный семиугольник не может быть построен с помощью циркуля и линейки , но может быть построен с помощью отмеченной линейки и циркуля. Это наименьший правильный многоугольник с этим свойством. Этот тип построения называется построением neusis . Он также может быть построен с помощью циркуля, линейки и трисектора угла. Невозможность построения с помощью линейки и циркуля следует из наблюдения, что является нулем неприводимой кубической функции x ³ + x ² − 2 x − 1 . Следовательно, этот многочлен является минимальным многочленом 2cos ( 2π ⁄ 7 ), тогда как степень минимального многочлена для конструктивного числа должна быть степенью 2. ${\displaystyle \scriptstyle {2\cos {\tfrac {2\pi }{7}}\approx 1.247}}$

Семиугольник с заданной длиной стороны :
анимация построения невзиса с отмеченной линейкой по Дэвиду Джонсону Лейску ( Крокетт Джонсон ).

Приближение

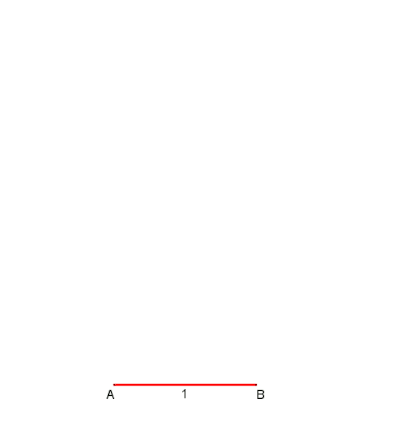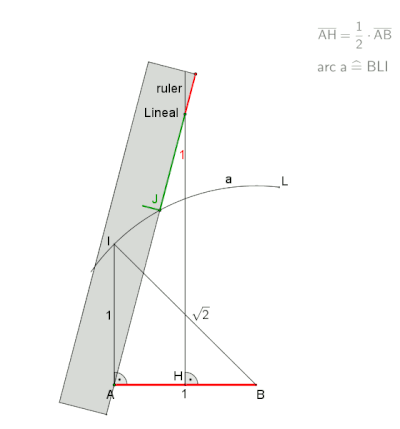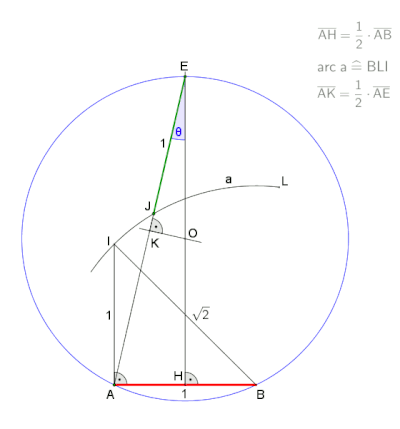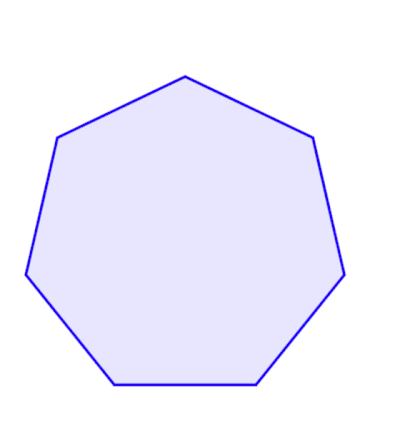
Приближение для практического использования с погрешностью около 0,2% заключается в использовании половины стороны равностороннего треугольника, вписанного в ту же окружность, что и длина стороны правильного семиугольника. Неизвестно, кто первым нашел это приближение, но оно было упомянуто Героном Александрийским в « Метрике» в I веке нашей эры, было хорошо известно средневековым исламским математикам и может быть найдено в работе Альбрехта Дюрера . ^{[2] [3]} Пусть A лежит на окружности описанной окружности. Начертим дугу BOC . Затем даем приближение для стороны семиугольника. ${\displaystyle \scriptstyle {BD={1 \over 2}BC}}$

Это приближение использует сторону семиугольника, вписанного в единичную окружность, тогда как точное значение равно . ${\displaystyle \scriptstyle {{\sqrt {3}} \over 2}\approx 0.86603}$ ${\displaystyle \scriptstyle 2\sin {\pi \over 7}\approx 0.86777}$

Пример, иллюстрирующий погрешность:
при радиусе описанной окружности r = 1 м абсолютная погрешность первой стороны составит приблизительно -1,7 мм.

Другие приближения

Существуют и другие приближения к семиугольнику с использованием циркуля и линейки, но их построение занимает много времени. ^[4]

Симметрия

Симметрии правильного семиугольника. Вершины окрашены в соответствии с их позициями симметрии. Синие зеркальные линии проведены через вершины и ребра. Порядки вращения даны в центре. ^[5]

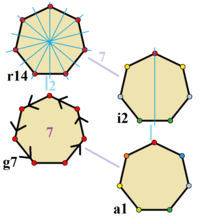
Правильный семиугольник принадлежит точечной группе D 7h ( обозначение Шёнфлиса ), порядок 28. Элементами симметрии являются: ось собственного вращения 7-го порядка C ₇ , ось несобственного вращения 7-го порядка S ₇ , 7 вертикальных плоскостей зеркального отражения σ _v , 7 осей вращения 2-го порядка C ₂ в плоскости семиугольника и горизонтальная плоскость зеркального отражения σ _h , также в плоскости семиугольника. ^[6]

Диагонали и семиугольный треугольник

a =красный, b =синий, c =зеленый линии

Сторона правильного семиугольника a , короткая диагональ b и длинная диагональ c , причем a < b < c , удовлетворяют ^{[7] : Лемма 1}

${\displaystyle a^{2}=c(c-b),}$

${\displaystyle b^{2}=a(c+a),}$

${\displaystyle c^{2}=b(a+b),}$

${\displaystyle {\frac {1}{a}}={\frac {1}{b}}+{\frac {1}{c}}}$ ( оптическое уравнение )

и, следовательно,

${\displaystyle ab+ac=bc,}$

и ^{[7] : Кор. 2}

${\displaystyle b^{3}+2b^{2}c-bc^{2}-c^{3}=0,}$

${\displaystyle c^{3}-2c^{2}a-ca^{2}+a^{3}=0,}$

${\displaystyle a^{3}-2a^{2}b-ab^{2}+b^{3}=0,}$

Таким образом, b / c , c / a и a / b удовлетворяют кубическому уравнению. Однако для решений этого уравнения не существует алгебраических выражений с чисто действительными членами, поскольку это пример casus unreducibilis . ${\displaystyle t^{3}-2t^{2}-t+1=0.}$

Приблизительные длины диагоналей в терминах сторон правильного семиугольника определяются по формуле

${\displaystyle b\approx 1.80193\cdot a,\qquad c\approx 2.24698\cdot a.}$

У нас также есть ^[8]

${\displaystyle b^{2}-a^{2}=ac,}$

${\displaystyle c^{2}-b^{2}=ab,}$

${\displaystyle a^{2}-c^{2}=-bc,}$

и

${\displaystyle {\frac {b^{2}}{a^{2}}}+{\frac {c^{2}}{b^{2}}}+{\frac {a^{2}}{c^{2}}}=5.}$

Семиугольный треугольник имеет вершины, совпадающие с первой, второй и четвертой вершинами правильного семиугольника (от произвольной начальной вершины), а углы и Таким образом, его стороны совпадают с одной стороной и двумя частными диагоналями правильного семиугольника. ^[7] ${\displaystyle \pi /7,2\pi /7,}$ ${\displaystyle 4\pi /7.}$

В многогранниках

За исключением семиугольной призмы и семиугольной антипризмы , ни один выпуклый многогранник, полностью состоящий из правильных многоугольников, не содержит семиугольник в качестве грани.

Звездные семиугольники

Из правильных семиугольников можно построить два вида звездчатых семиугольников ( гептаграмм ), обозначенных символами Шлефли {7/2} и {7/3}, при этом делителем является интервал соединения.

Синие, {7/2} и зеленые {7/3} звездчатые семиугольники внутри красного семиугольника.

Укладка плитки и упаковка

Правильный треугольник, семиугольник и 42-угольник могут полностью заполнить вершину плоскости . Однако, нет мозаики плоскости только этими многоугольниками, потому что нет способа поместить один из них на третью сторону треугольника, не оставляя зазора или не создавая наложения. В гиперболической плоскости возможны мозаики правильными семиугольниками. Также возможны мозаики вогнутыми семиугольниками в евклидовой плоскости. ^[9]

Самая плотная двойная решетчатая упаковка евклидовой плоскости правильными семиугольниками, предположительно имеющая самую низкую максимальную плотность упаковки среди всех выпуклых множеств.

Правильный семиугольник имеет двойную решетчатую упаковку евклидовой плоскости с плотностью упаковки приблизительно 0,89269. Было высказано предположение, что это наименьшая возможная плотность для оптимальной двойной решетчатой ​​плотности упаковки любого выпуклого множества, и в более общем смысле для оптимальной плотности упаковки любого выпуклого множества. ^[10]

Эмпирические примеры

В Соединенном Королевстве с 1982 года выпускаются две семиугольные монеты : 50 и 20 пенсов. Барбадосский доллар также имеет семиугольную форму. Строго говоря, форма монет представляет собой семиугольник Рёло , криволинейный семиугольник с изгибами постоянной ширины ; стороны изогнуты наружу, чтобы монеты могли плавно катиться, когда их вставляют в торговый автомат . Монеты ботсванской пулы достоинством 2 пулы, 1 пула, 50 тхэбэ и 5 тхэбэ также имеют форму равносторонних криволинейных семиугольников. Монеты в форме семиугольников Рёло также находятся в обращении на Маврикии, в ОАЭ, Танзании, Самоа, Папуа-Новой Гвинее, Сан-Томе и Принсипи, на Гаити, Ямайке, в Либерии, Гане, Гамбии, Иордании, Джерси, Гернси, на острове Мэн, в Гибралтаре, Гайане, на Соломоновых островах, на Фолклендских островах и на острове Святой Елены. Монета в 1000 квач Замбии представляет собой настоящий семиугольник.

Бразильская монета в 25 центов имеет семиугольник , вписанный в диск монеты. Некоторые старые версии герба Грузии , в том числе в советские времена , использовали {7/2} гептаграмму в качестве элемента.

Ряд монет, включая монету в 20 евроцентов , имеют семиугольную симметрию в форме, называемой испанским цветком .

В архитектуре семиугольные планы этажей встречаются очень редко. Замечательным примером является Мавзолей принца Эрнста в Штадтхагене , Германия .

Многие полицейские значки в США имеют контур гептаграммы {7/2}.

Смотрите также

• Гептаграмма
• Полигон

Ссылки

1. Gleason, Andrew Mattei (март 1988). «Angle trisection, the heptagon, and the triskaidecagon p. 186 (Fig.1) –187» (PDF) . The American Mathematical Monthly . 95 (3): 185–194. doi :10.2307/2323624. JSTOR  2323624. Архивировано из оригинала (PDF) 19 декабря 2015 г.
2. Хогендейк, Ян П. (1987). «Ответ Абу-ль-Джуда на вопрос аль-Бируни о правильном семиугольнике» (PDF) . Анналы Нью-Йоркской академии наук . 500 (1): 175–183. doi :10.1111/j.1749-6632.1987.tb37202.x.
3. GH Hughes, «Многоугольники Альбрехта Дюрера-1525, Правильный семиугольник», рис. 11, сторона семиугольника (7) рис. 15, изображение на левой стороне, получено 4 декабря 2015 г.
4. Рауманнкидвай. "Семиугольник." Диаграмма. Геогебра. По состоянию на 20 января 2024 г. https://www.geogebra.org/classic/CvsudDWr.
5. Джон Х. Конвей, Хайди Бергиль, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278) 
6. Salthouse, JA; Ware, MJ (1972). Таблицы символов точечной группы и связанные с ними данные. Кембридж: Cambridge University Press. ISBN 0-521-08139-4.
7. Абдилкадир Алтинтас, «Некоторые коллинеарности в семиугольном треугольнике», Forum Geometricorum 16, 2016, 249–256.http://forumgeom.fau.edu/FG2016volume16/FG201630.pdf
8. Леон Бэнкофф и Джек Гарфанкел, «Семиугольный треугольник», Mathematics Magazine 46 (1), январь 1973 г., 7–19.
9. Sycamore916, ред. «Heptagon». Polytope Wiki. Последнее изменение: ноябрь 2023 г. Доступ: 20 января 2024 г. https://polytope.miraheze.org/wiki/Heptagon/Heptagon.
10. Каллус, Йоав (2015). «Пессимальные формы упаковки». Геометрия и топология . 19 (1): 343–363. arXiv : 1305.0289 . doi :10.2140/gt.2015.19.343. MR  3318753.

Внешние ссылки

• Определение и свойства семиугольника С интерактивной анимацией
• Гептагон по Джонсону
• Другой приблизительный метод построения
• Многоугольники – Семиугольники
• Недавно обнаруженное и высокоточное приближение для построения правильного семиугольника.
• Семиугольник, аппроксимирующая конструкция в виде анимации
• Семиугольник с заданной стороной, аппроксимирующая конструкция в виде анимации

Семиугольник