Термодинамическая температура

Мера температуры относительно абсолютного нуля

Термодинамическая температура — это величина, определяемая в термодинамике в отличие от кинетической теории или статистической механики .

Исторически термодинамическая температура была определена лордом Кельвином в терминах макроскопического соотношения между термодинамической работой и теплопередачей , как определено в термодинамике, но кельвин был переопределен международным соглашением в 2019 году в терминах явлений, которые теперь понимаются как проявления кинетической энергии свободного движения микроскопических частиц, таких как атомы, молекулы и электроны. С термодинамической точки зрения, по историческим причинам, из-за того, как оно определяется и измеряется, это микроскопическое кинетическое определение рассматривается как «эмпирическая» температура. Оно было принято, потому что на практике его, как правило, можно измерить точнее, чем термодинамическую температуру Кельвина.

Термодинамическая температура, равная нулю, имеет особое значение для третьего закона термодинамики . По соглашению она указывается на шкале температур Кельвина , в которой единицей измерения является кельвин (символ единицы: K). Для сравнения, температура 295 K соответствует 21,85 °C и 71,33 °F.

Обзор

Термодинамическая температура, в отличие от температуры СИ, определяется в терминах макроскопического цикла Карно . Термодинамическая температура важна в термодинамике, поскольку она определяется в чисто термодинамических терминах. Температура СИ концептуально сильно отличается от термодинамической температуры. Термодинамическая температура была строго определена исторически задолго до того, как появились достаточные знания о микроскопических частицах, таких как атомы, молекулы и электроны.

Международная система единиц (СИ) определяет международную абсолютную шкалу для измерения температуры и единицу измерения кельвин (символ единицы: K) для определенных значений по шкале. Кельвин также используется для обозначения температурных интервалов (разница или разница между двумя температурами) в соответствии со следующим примером использования: «Припой олово/свинец 60/40 не является эвтектическим и пластичен в диапазоне 5 кельвинов при затвердевании». Температурный интервал в один градус Цельсия имеет ту же величину, что и один кельвин.

Величина кельвина была переопределена в 2019 году в связи с физическим свойством, лежащим в основе термодинамической температуры: кинетической энергией движения атомных свободных частиц. Пересмотр зафиксировал постоянную Больцмана точно на уровне1,380 649 × 10 ⁻²³  джоулей на кельвин (Дж/К). ^[1]

Микроскопическое свойство, которое наделяет материальные субстанции температурой, можно легко понять, изучив закон идеального газа , который описывает, согласно постоянной Больцмана, как тепловая энергия вызывает точно определенные изменения давления и температуры определенных газов. Это происходит потому, что одноатомные газы, такие как гелий и аргон, ведут себя кинетически как свободно движущиеся идеально упругие и сферические бильярдные шары, которые движутся только в определенном подмножестве возможных движений, которые могут происходить в материи: включающем три поступательные степени свободы . Поступательные степени свободы — это знакомые движения, подобные бильярдным шарам, вдоль осей X, Y и Z трехмерного пространства (см. рис. 1 ниже). Вот почему все благородные газы имеют одинаковую удельную теплоемкость на атом и почему это значение является самым низким среди всех газов.

Молекулы (два или более химически связанных атома), однако, имеют внутреннюю структуру и, следовательно, имеют дополнительные внутренние степени свободы (см. рис. 3 ниже), что заставляет молекулы поглощать больше тепловой энергии для любого заданного количества повышения температуры, чем одноатомные газы. Тепловая энергия рождается во всех доступных степенях свободы; это соответствует теореме о равнораспределении , поэтому все доступные внутренние степени свободы имеют ту же температуру, что и их три внешние степени свободы. Однако свойство, которое дает всем газам их давление , которое является чистой силой на единицу площади на контейнере, возникающей из-за отскакивания от него частиц газа, является функцией кинетической энергии, переносимой в трех поступательных степенях свободы свободно движущихся атомов и молекул. ^[2]

Фиксация постоянной Больцмана на определенном значении, наряду с другими правилами, имела эффект точного установления величины единичного интервала температуры СИ, кельвина, с точки зрения среднего кинетического поведения благородных газов. Более того, начальная точка термодинамической температурной шкалы, абсолютный ноль, была подтверждена как точка, в которой в образце остается нулевая средняя кинетическая энергия ; единственным оставшимся движением частиц является то, что включает случайные колебания из-за энергии нулевой точки.

Абсолютный ноль температуры

Температурные шкалы являются числовыми. Числовой ноль температурной шкалы не привязан к абсолютному нулю температуры. Тем не менее, некоторые температурные шкалы имеют свой числовой ноль, совпадающий с абсолютным нулем температуры. Примерами являются Международная температурная шкала СИ, температурная шкала Ранкина и термодинамическая температурная шкала. Другие температурные шкалы имеют свой числовой ноль далеко от абсолютного нуля температуры. Примерами являются шкала Фаренгейта и шкала Цельсия.

В нулевой точке термодинамической температуры, абсолютном нуле , частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее. ^{[3] [4]} Абсолютный ноль, который является температурой ноль кельвинов (0 К), точно соответствует −273,15 °C и −459,67 °F. Материя при абсолютном нуле не имеет остаточной передаваемой средней кинетической энергии, и единственное остаточное движение частиц обусловлено постоянно распространяющимся квантово-механическим явлением, называемым ZPE ( энергия нулевой точки ). ^[5] Хотя атомы, например, в контейнере с жидким гелием , который был точно при абсолютном нуле, все еще слегка толкались бы из-за энергии нулевой точки, теоретически совершенная тепловая машина с таким гелием в качестве одной из своих рабочих жидкостей никогда не могла бы передать никакой чистой кинетической энергии ( тепловой энергии ) другой рабочей жидкости, и никакая термодинамическая работа не могла бы быть выполнена.

Температура обычно выражается в абсолютных величинах при научном изучении взаимосвязей температуры с некоторыми другими физическими свойствами материи, такими как ее объем или давление (см. закон Гей-Люссака ) или длина волны испускаемого ею излучения черного тела . Абсолютная температура также полезна при расчете скоростей химических реакций (см. уравнение Аррениуса ). Кроме того, абсолютная температура обычно используется в криогенике и связанных с ней явлениях, таких как сверхпроводимость , как в следующем примере использования: «Удобно, что температура перехода тантала ( T _c ) 4,4924 кельвина немного выше точки кипения гелия 4,2221 К».

постоянная Больцмана

Постоянная Больцмана и связанные с ней формулы описывают область кинетики частиц и векторов скорости, тогда как ZPE ( энергия нулевой точки ) — это энергетическое поле, которое толкает частицы способами, описываемыми математикой квантовой механики. В атомных и молекулярных столкновениях в газах ZPE вносит степень хаоса , т. е. непредсказуемости, в кинетику отскока; вполне вероятно, что после данного столкновения будет меньше движения частиц, вызванного ZPE, чем больше . Эта случайная природа ZPE является причиной того, что она не оказывает никакого чистого эффекта ни на давление, ни на объем любого объемного количества (статистически значимого количества частиц) газов. Однако в конденсированном веществе при температуре T = 0 ; например, в твердых телах и жидкостях, ZPE вызывает межатомное толкание, где атомы в противном случае были бы совершенно неподвижны. Поскольку реальные эффекты, которые энергия нулевой энергии оказывает на вещества, могут меняться при изменении термодинамической системы (например, из-за энергии нулевой энергии гелий замерзает только под давлением не менее 2,5  МПа (25  бар )), энергия нулевой энергии по сути является формой тепловой энергии и может быть правильно включена при подсчете внутренней энергии вещества.

шкала Рэнкина

Хотя на протяжении всей истории существовало множество других температурных шкал , для измерения термодинамической температуры существуют только две шкалы, имеющие в качестве нулевой точки (0) абсолютный ноль: шкала Кельвина и шкала Ренкина.

В научном мире, где современные измерения почти всегда производятся с использованием Международной системы единиц, термодинамическая температура измеряется с использованием шкалы Кельвина. Шкала Ранкина является частью английских инженерных единиц и находит применение в определенных областях техники, особенно в устаревших справочных работах. Шкала Ранкина использует в качестве единицы градус Ранкина (символ: °R), который имеет ту же величину, что и градус Фаренгейта (символ: °F).

Единица приращения в один кельвин равна ровно 1,8 умножить на один градус Ранкина; таким образом, для перевода определенной температуры по шкале Кельвина в шкалу Ранкина x K = 1,8 x °R , а для перевода из температуры по шкале Ранкина в шкалу Кельвина x °R = x /1,8 K. Следовательно, абсолютный ноль равен «0» для обеих шкал, но точка плавления водяного льда (0 °C и 273,15 K) равна 491,67 °R.

Для преобразования температурных интервалов (разницы или разницы между двумя температурами) применимы формулы из предыдущего абзаца; например, интервал в 5 кельвинов в точности равен интервалу в 9 градусов Ренкина.

Современное переопределение кельвина

В течение 65 лет, с 1954 по 2019 год, в период с пересмотра СИ , температурный интервал в один кельвин определялся как ⁠1/273.16⁠ разница между тройной точкой воды и абсолютным нулем. Резолюция Международного бюро мер и весов 1954 года (известного по франкоязычной аббревиатуре BIPM), а также более поздние резолюции и публикации определили тройную точку воды как точно 273,16 К и признали, что «обычной практикой» является принятие этого в силу предыдущих соглашений (а именно, что 0 °C долгое время определялось как точка плавления воды и что тройная точка воды давно экспериментально определена как неразличимо близкая к 0,01 °C), разница между шкалой Цельсия и шкалой Кельвина принимается равной 273,15 кельвина; то есть 0 °C соответствует 273,15 кельвина. ^[6] Чистый эффект этого, а также более поздних постановлений был двояким: 1) они определили абсолютный ноль как точно 0 К, и 2) они определили, что тройная точка специальной изотопно-контролируемой воды, называемой Венской стандартной средней океанической водой, находится точно при 273,16 К и 0,01 °C. Одним из эффектов вышеупомянутых постановлений было то, что точка плавления воды, хотя и очень близка к 273,15 К и 0 °C, не была определяющим значением и подлежала уточнению с помощью более точных измерений.

Стандарт BIPM 1954 года проделал хорошую работу по установлению — в пределах неопределенностей, вызванных изотопными изменениями между образцами воды — температур около точек замерзания и тройной точки воды, но требовал, чтобы промежуточные значения между тройной точкой и абсолютным нулем, а также экстраполированные значения от комнатной температуры и выше, были экспериментально определены с помощью аппаратуры и процедур в отдельных лабораториях. Этот недостаток был устранен Международной температурной шкалой 1990 года , или ITS-90, которая определила 13 дополнительных точек, от 13,8033 К до 1357,77 К. Несмотря на то, что ITS-90 была определяющей, у нее были — и все еще есть — некоторые проблемы, отчасти потому, что восемь из ее экстраполированных значений зависят от точек плавления или замерзания металлических образцов, которые должны оставаться чрезвычайно чистыми, чтобы их точки плавления или замерзания не были затронуты — обычно пониженными.

Пересмотр СИ 2019 года был в первую очередь направлен на то, чтобы отделить большую часть основ определения системы СИ от килограмма , который был последним физическим артефактом, определяющим базовую единицу СИ (цилиндр из платины/иридия, хранившийся под тремя вложенными друг в друга стеклянными колпаками в сейфе, расположенном во Франции) и чья стабильность была весьма сомнительной. Решение требовало, чтобы четыре физические константы, включая постоянную Больцмана, были по определению зафиксированы.

Присвоение постоянной Больцмана точно определенного значения не имело практического эффекта на современную термометрию, за исключением самых изысканно точных измерений. До пересмотра тройная точка воды была равна точно 273,16 К и 0,01 °C, а постоянная Больцмана была экспериментально определена как1,380 649 03 (51) × 10 ⁻²³  Дж/К , где «(51)» обозначает неопределенность в двух младших значащих цифрах (03) и равняется относительной стандартной неопределенности 0,37 ppm. ^[7] Затем, определив постоянную Больцмана как точно1,380 649 × 10 ⁻²³  Дж/К , неопределенность 0,37 ppm была перенесена в тройную точку воды, которая стала экспериментально определенным значением273,1600 ± 0,0001 К (0,0100 ± 0,0001 °C ). То, что тройная точка воды оказалась чрезвычайно близкой к 273,16 К после пересмотра СИ, не было случайностью; окончательное значение постоянной Больцмана было определено, в частности, с помощью хитроумных экспериментов с аргоном и гелием, в которых тройная точка воды использовалась в качестве ключевой опорной температуры. ^{[8] [9]}

Несмотря на пересмотр 2019 года, ячейки тройной точки воды продолжают служить в современной термометрии в качестве чрезвычайно точных калибровочных эталонов при 273,16 К и 0,01 °C. Более того, тройная точка воды остается одной из 14 калибровочных точек, составляющих ITS‑90, которая простирается от тройной точки водорода (13,8033 К) до точки замерзания меди (1357,77 К), что составляет почти стократный диапазон термодинамической температуры.

Взаимосвязь температуры, движения, проводимости и тепловой энергии

Рисунок 1 Поступательное движение фундаментальных частиц природы, таких как атомы и молекулы, напрямую связано с температурой. Здесь размер атомов гелия относительно их расстояния показан в масштабе при давлении 1950 атмосфер . Эти атомы при комнатной температуре имеют определенную среднюю скорость (здесь замедленную в два триллиона раз). Однако в любой момент времени конкретный атом гелия может двигаться намного быстрее средней, в то время как другой может быть почти неподвижен. Пять атомов окрашены в красный цвет, чтобы облегчить отслеживание их движений. Эта анимация иллюстрирует статистическую механику , которая является наукой о том, как групповое поведение большой совокупности микроскопических объектов возникает из кинетических свойств каждого отдельного объекта.

Природа кинетической энергии, поступательного движения и температуры

Термодинамическая температура любого объемного количества вещества (статистически значимого количества частиц) прямо пропорциональна средней кинетической энергии определенного вида движения частиц, известного как поступательное движение . Эти простые движения в трех измерениях осей X, Y и Z пространства означают, что частицы движутся в трех пространственных степенях свободы . Эту конкретную форму кинетической энергии иногда называют кинетической температурой . Поступательное движение — это всего лишь одна из форм тепловой энергии, и именно она придает газам не только их температуру, но также их давление и большую часть их объема. Эта связь между температурой, давлением и объемом газов устанавливается формулой закона идеального газа pV = nRT и воплощена в газовых законах .

Хотя кинетическая энергия, переносимая исключительно в трех поступательных степенях свободы, составляет термодинамическую температуру вещества, молекулы, как можно видеть на рис. 3, могут иметь и другие степени свободы, все из которых попадают в три категории: длина связи, угол связи и вращательная. Все три дополнительные категории не обязательно доступны всем молекулам, и даже для молекул, которые могут испытывать все три, некоторые могут быть «заморожены» ниже определенной температуры. Тем не менее, все те степени свободы, которые доступны молекулам при определенном наборе условий, вносят вклад в удельную теплоемкость вещества; то есть они увеличивают количество тепла (кинетическую энергию), необходимое для повышения заданного количества вещества на один кельвин или один градус Цельсия.

Связь кинетической энергии, массы и скорости определяется формулой E _k  =  ⁠1/2⁠ mv ² . ^[10] Соответственно, частицы с одной единицей массы, движущиеся с одной единицей скорости, имеют точно такую ​​же кинетическую энергию и точно такую ​​же температуру, как и частицы с четырехкратной массой, но в два раза меньшей скоростью.

Степень, в которой кинетическая энергия поступательного движения в статистически значимом наборе атомов или молекул в газе вносит вклад в давление и объем этого газа, является пропорциональной функцией термодинамической температуры, как установлено постоянной Больцмана (символ:  k _B ). Постоянная Больцмана также связывает термодинамическую температуру газа со средней кинетической энергией поступательного движения отдельных частиц следующим образом: где: $${\displaystyle {\tilde {E}}={\frac {3}{2}}k_{\text{B}}T}$$

• ${\textstyle {\tilde {E}}}$это средняя кинетическая энергия для отдельной частицы
• к _Б =1,380 649 × 10−23 Дж ^/  К
• T — термодинамическая температура основного количества вещества

Рисунок 2. Поступательные движения атомов гелия происходят в диапазоне скоростей. Сравните форму этой кривой с формой кривой Планка на рис. 5 ниже.

Хотя постоянная Больцмана полезна для нахождения средней кинетической энергии в образце частиц, важно отметить, что даже когда вещество изолировано и находится в термодинамическом равновесии (все части имеют одинаковую температуру и тепло не поступает в него или не выходит из него), поступательные движения отдельных атомов и молекул происходят в широком диапазоне скоростей (см. анимацию на рис. 1 выше). В любой момент времени доля частиц, движущихся с заданной скоростью в этом диапазоне, определяется вероятностью, как описано распределением Максвелла–Больцмана . График, показанный здесь на рис. 2, показывает распределение скоростей атомов гелия при температуре 5500 К. Их наиболее вероятная скорость составляет 4,780 км/с (0,2092 с/км). Однако определенная доля атомов в любой момент времени движутся быстрее, в то время как другие движутся относительно медленно; некоторые на мгновение фактически останавливаются (вне оси x справа). Этот график использует обратную скорость для своей оси x , поэтому форму кривой можно легко сравнить с кривыми на рис. 5 ниже. На обоих графиках ноль на оси x представляет бесконечную температуру. Кроме того, оси x и y на обоих графиках масштабируются пропорционально.

Высокие скорости поступательного движения

Хотя для прямого обнаружения поступательных движений требуется очень специализированное лабораторное оборудование, возникающие столкновения атомов или молекул с мелкими частицами, взвешенными в жидкости, производят броуновское движение , которое можно увидеть с помощью обычного микроскопа. Поступательные движения элементарных частиц очень быстры ^[11] , и для их непосредственного наблюдения требуются температуры, близкие к абсолютному нулю . Например, когда ученые из NIST достигли рекордной холодной температуры 700 нК (миллиардные доли кельвина) в 1994 году, они использовали оптическое решеточное лазерное оборудование для адиабатического охлаждения атомов цезия . Затем они выключили лазеры захвата и напрямую измерили скорости атомов 7 мм в секунду, чтобы вычислить их температуру. ^[12] Формулы для расчета скорости и скорости поступательного движения приведены в следующей сноске. ^[13]

Рисунок 2.5 Эта симуляция иллюстрирует атом аргона, как он будет выглядеть через оптический микроскоп с увеличением 400, имеющий сетку с делениями 50 микрон (0,05 мм). Этот атом движется со скоростью 14,43 микрона в секунду, что дает атому кинетическую температуру в одну триллионную кельвина. Атому требуется 13,9 секунды, чтобы пройти 200 микрон (0,2 мм). Хотя атом невидимо толкается из-за энергии нулевой точки, его поступательное движение, наблюдаемое здесь, включает в себя всю его кинетическую энергию.

Нетрудно представить себе атомные движения, вызванные кинетической температурой, и отличить такие движения от движений, вызванных энергией нулевой точки. Рассмотрим следующий гипотетический мысленный эксперимент, как показано на рис. 2.5 слева, с атомом, который чрезвычайно близок к абсолютному нулю. Представьте, что вы смотрите в обычный оптический микроскоп, установленный на 400-кратное увеличение, что примерно соответствует максимальному практическому увеличению для оптических микроскопов. Такие микроскопы обычно обеспечивают поля зрения диаметром чуть более 0,4 мм. В центре поля зрения находится один левитирующий атом аргона (аргон составляет около 0,93% воздуха), который освещен и светится на темном фоне. Если бы этот атом аргона находился на рекордной одной триллионной кельвина выше абсолютного нуля ^[14] и двигался перпендикулярно полю зрения вправо, ему потребовалось бы 13,9 секунды, чтобы переместиться из центра изображения до отметки в 200 микрон; это расстояние перемещения примерно равно ширине точки в конце этого предложения на современных компьютерных мониторах. Поскольку атом аргона медленно двигался, позиционное дрожание из-за энергии нулевой точки было бы намного меньше, чем разрешение оптического микроскопа в 200 нанометров (0,0002 мм). Важно отметить, что поступательная скорость атома 14,43 микрон в секунду составляет всю его сохраненную кинетическую энергию из-за того, что он не находится точно при абсолютном нуле. Если бы атом был точно при абсолютном нуле, незаметные толчки из-за энергии нулевой точки заставили бы его слегка блуждать, но атом постоянно находился бы, в среднем, в одном и том же месте в поле зрения. Это аналогично лодке, у которой выключили мотор и теперь она слегка покачивается в относительно спокойных и безветренных водах океана; даже если лодка беспорядочно дрейфует туда-сюда, она остается на одном и том же месте в долгосрочной перспективе и не продвигается вперед по воде. Соответственно, атом, который был бы точно при абсолютном нуле, не был бы «неподвижным», и все же статистически значимая совокупность таких атомов имела бы нулевую чистую кинетическую энергию, доступную для передачи любой другой совокупности атомов. Это происходит потому, что независимо от кинетической температуры второй совокупности атомов, они также испытывают воздействие энергии нулевой точки. Таковы следствия статистической механики и природы термодинамики.

Внутренние движения молекул и внутренняя энергия

Рисунок 3 Молекулы имеют внутреннюю структуру, поскольку они состоят из атомов, которые имеют различные способы движения внутри молекул. Способность хранить кинетическую энергию в этих внутренних степенях свободы способствует удельной теплоемкости вещества , или внутренней энергии, позволяя ему содержать больше внутренней энергии при той же температуре.

Как упоминалось выше, существуют и другие способы, которыми молекулы могут колебаться, помимо трех поступательных степеней свободы, которые наделяют вещества их кинетической температурой. Как можно увидеть на анимации справа, молекулы являются сложными объектами; они представляют собой популяцию атомов, и тепловое возбуждение может напрягать их внутренние химические связи тремя различными способами: через вращение, длину связи и движение угла связи; все это типы внутренних степеней свободы . Это отличает молекулы от одноатомных веществ (состоящих из отдельных атомов), таких как благородные газы гелий и аргон , которые имеют только три поступательные степени свободы (оси X, Y и Z). Кинетическая энергия хранится во внутренних степенях свободы молекул, что дает им внутреннюю температуру . Несмотря на то, что эти движения называются «внутренними», внешние части молекул все еще движутся — скорее как покачивание неподвижного водяного шарика . Это обеспечивает двусторонний обмен кинетической энергией между внутренними движениями и поступательными движениями при каждом молекулярном столкновении. Соответственно, по мере удаления внутренней энергии из молекул, как их кинетическая температура (кинетическая энергия поступательного движения), так и их внутренняя температура одновременно уменьшаются в равных пропорциях. Это явление описывается теоремой о равнораспределении , которая гласит, что для любого объемного количества вещества в равновесии кинетическая энергия движения частиц равномерно распределена между всеми активными степенями свободы, доступными частицам. Поскольку внутренняя температура молекул обычно равна их кинетической температуре, это различие обычно представляет интерес только при детальном изучении явлений нелокального термодинамического равновесия (ЛТР), таких как горение , сублимация твердых тел и диффузия горячих газов в частичном вакууме.

Кинетическая энергия, хранящаяся внутри молекул, заставляет вещества содержать больше тепловой энергии при любой заданной температуре и поглощать дополнительную внутреннюю энергию для заданного повышения температуры. Это происходит потому, что любая кинетическая энергия, которая в заданный момент времени связана во внутренних движениях, не способствует поступательному движению молекул в тот же момент времени. ^{[15] Эта дополнительная кинетическая энергия просто увеличивает количество внутренней энергии, которую вещество поглощает для заданного повышения температуры. Это свойство известно как} удельная теплоемкость вещества .

Различные молекулы поглощают разное количество внутренней энергии при каждом постепенном повышении температуры; то есть они имеют разную удельную теплоемкость. Высокая удельная теплоемкость возникает, отчасти, потому что молекулы некоторых веществ обладают большим количеством внутренних степеней свободы, чем другие. Например, азот при комнатной температуре , который является двухатомной молекулой, имеет пять активных степеней свободы: три, включающие поступательное движение, плюс две вращательные степени свободы внутри. Неудивительно, что в соответствии с теоремой о равнораспределении азот имеет пять третей удельной теплоемкости на моль (определенное число молекул), как и одноатомные газы. ^[16] Другим примером является бензин (см. таблицу , показывающую его удельную теплоемкость). Бензин может поглощать большое количество тепловой энергии на моль при лишь скромном изменении температуры, потому что каждая молекула состоит в среднем из 21 атома и, следовательно, имеет много внутренних степеней свободы. Даже более крупные, более сложные молекулы могут иметь десятки внутренних степеней свободы.

Диффузия тепловой энергии: энтропия, фононы и подвижные электроны проводимости

Рисунок 4. Температурно-индуцированное поступательное движение частиц в твердых телах принимает форму фононов . Здесь показаны фононы с одинаковыми амплитудами , но с длинами волн в диапазоне от 2 до 12 средних межмолекулярных расстояний ( a ).

Теплопроводность — это диффузия тепловой энергии от горячих частей системы к холодным. Система может быть как единым объемным образованием, так и множеством дискретных объемных образований. Термин « объем» в этом контексте означает статистически значимое количество частиц (которое может быть микроскопическим). Всякий раз, когда тепловая энергия распространяется внутри изолированной системы, разница температур внутри системы уменьшается (а энтропия увеличивается).

Один конкретный механизм теплопроводности происходит, когда поступательное движение, движение частиц, лежащее в основе температуры, передает импульс от частицы к частице при столкновениях. В газах эти поступательные движения имеют природу, показанную выше на рис. 1. Как можно видеть на этой анимации, не только импульс (тепло) распространяется по всему объему газа посредством последовательных столкновений, но и целые молекулы или атомы могут перемещаться вперед на новую территорию, принося с собой свою кинетическую энергию. Следовательно, разность температур выравнивается по всему газу очень быстро — особенно для легких атомов или молекул; конвекция еще больше ускоряет этот процесс. ^[17]

Однако поступательное движение в твердых телах принимает форму фононов (см. рис. 4 справа). Фононы — это ограниченные, квантованные волновые пакеты, которые движутся со скоростью звука данного вещества. То, как фононы взаимодействуют внутри твердого тела, определяет множество его свойств, включая его теплопроводность. В электроизолирующих твердых телах теплопроводность на основе фононов обычно неэффективна [ ^18], и такие твердые тела считаются теплоизоляторами (например, стекло, пластик, резина, керамика и камень). Это связано с тем, что в твердых телах атомы и молекулы зафиксированы на месте относительно своих соседей и не могут свободно перемещаться.

Однако металлы не ограничиваются только теплопроводностью на основе фононов. Тепловая энергия проходит через металлы необычайно быстро, потому что вместо прямых столкновений молекул с молекулами подавляющее большинство тепловой энергии передается через очень легкие, подвижные электроны проводимости . Вот почему существует почти идеальная корреляция между теплопроводностью металлов и их электропроводностью . ^[19] Электроны проводимости наделяют металлы их необычайной проводимостью, потому что они делокализованы ( т. е. не привязаны к определенному атому) и ведут себя скорее как своего рода квантовый газ из-за эффектов энергии нулевой точки (подробнее о ZPE см. в примечании 1 ниже). Кроме того, электроны относительно легкие, с массой покоя всего 1 ⁄ 1836 массы протона . Это примерно то же самое соотношение, что и у пули .22 Short (29 гран или 1,88  г ) по сравнению с винтовкой, из которой она стреляет. Как писал Исаак Ньютон в своем третьем законе движения ,

Закон № 3: Все силы действуют парами, и эти две силы равны по величине и противоположны по направлению.

Однако пуля ускоряется быстрее, чем винтовка при равной силе. Поскольку кинетическая энергия увеличивается как квадрат скорости, почти вся кинетическая энергия уходит в пулю, а не в винтовку, хотя обе испытывают одинаковую силу от расширяющихся пороховых газов. Таким же образом, поскольку они гораздо менее массивны, тепловая энергия легко переносится подвижными электронами проводимости. Кроме того, поскольку они делокализованы и очень быстры, кинетическая тепловая энергия чрезвычайно быстро проводится через металлы с обильными электронами проводимости.

Распространение тепловой энергии: излучение черного тела

Рисунок 5 Спектр излучения черного тела имеет форму кривой Планка. Черное тело с температурой 5500 К имеет пиковую длину волны излучения 527 нм. Сравните форму этой кривой с формой распределения Максвелла на рис. 2  выше.

Тепловое излучение является побочным продуктом столкновений, возникающих в результате различных колебательных движений атомов. Эти столкновения заставляют электроны атомов испускать тепловые фотоны (известные как излучение черного тела ). Фотоны испускаются всякий раз, когда электрический заряд ускоряется (как это происходит при столкновении электронных облаков двух атомов). Даже отдельные молекулы с внутренней температурой выше абсолютного нуля также испускают излучение черного тела из своих атомов. В любом большом количестве вещества, находящегося в равновесии, фотоны черного тела испускаются в диапазоне длин волн в спектре, имеющем форму колоколообразной кривой, называемой кривой Планка (см. график на рис. 5 справа). Вершина кривой Планка ( пиковая длина волны излучения ) расположена в определенной части электромагнитного спектра в зависимости от температуры черного тела. Вещества при экстремально криогенных температурах излучают на длинных радиоволнах, тогда как при экстремально высоких температурах производятся короткие гамма-лучи (см. § Таблица термодинамических температур).

Излучение черного тела рассеивает тепловую энергию по всему веществу, поскольку фотоны поглощаются соседними атомами, передавая импульс в этом процессе. Фотоны черного тела также легко покидают вещество и могут быть поглощены окружающей средой; кинетическая энергия при этом теряется.

Как установлено законом Стефана-Больцмана , интенсивность излучения черного тела увеличивается как четвертая степень абсолютной температуры. Таким образом, черное тело при температуре 824 К (чуть ниже тускло-красного свечения) излучает в 60 раз больше мощности, чем при 296 К (комнатная температура). Вот почему можно так легко почувствовать тепловое излучение от горячих объектов на расстоянии. При более высоких температурах, таких как те, которые обнаруживаются в лампе накаливания , излучение черного тела может быть основным механизмом, посредством которого тепловая энергия покидает систему.

Таблица термодинамических температур

В таблице ниже показаны различные точки термодинамической шкалы в порядке возрастания температуры.

1. Для абсолютно черного тела (которым вольфрамовые нити не являются). Излучательная способность вольфрамовых нитей больше на более коротких длинах волн, что делает их более белыми.
2. Значение 2500 К является приблизительным.
3. Эффективная температура фотосферы.
4. Для истинно черного тела (которым плазма не была). Доминирующее излучение Z-машины возникло из 40 МК электронов (мягкое рентгеновское излучение) внутри плазмы.

Тепло фазовых переходов

Рисунок 6 Лед и вода: две фазы одного и того же вещества

Кинетическая энергия движения частиц — это всего лишь один из факторов, вносящих вклад в общую тепловую энергию вещества; другой — фазовые переходы , которые представляют собой потенциальную энергию молекулярных связей, которые могут образовываться в веществе при его охлаждении (например, при конденсации и замерзании ). Тепловая энергия, необходимая для фазового перехода, называется скрытой теплотой . Это явление можно легче понять, рассмотрев его в обратном направлении: скрытая теплота — это энергия, необходимая для разрыва химических связей (например, при испарении и плавлении ). Почти каждый знаком с эффектами фазовых переходов; например, пар при температуре 100 °C может вызвать серьезные ожоги гораздо быстрее, чем воздух при температуре 100 °C из фена . Это происходит из-за того, что большое количество скрытой теплоты высвобождается при конденсации пара в жидкую воду на коже.

Несмотря на то, что тепловая энергия выделяется или поглощается во время фазовых переходов, чистые химические элементы , соединения и эвтектические сплавы не демонстрируют никаких изменений температуры, пока они подвергаются им (см. рис. 7 , справа внизу). Рассмотрим один конкретный тип фазового перехода: плавление. Когда твердое тело плавится, химические связи кристаллической решетки разрываются; вещество переходит из того, что известно как более упорядоченное состояние, в менее упорядоченное состояние . На рис. 7 плавление льда показано в нижнем левом поле с заголовком от синего к зеленому.

Рисунок 7 Температура воды не меняется во время фазовых переходов, когда тепло поступает в нее или выходит из нее. Полная теплоемкость моля воды в жидкой фазе (зеленая линия) составляет 7,5507 кДж.

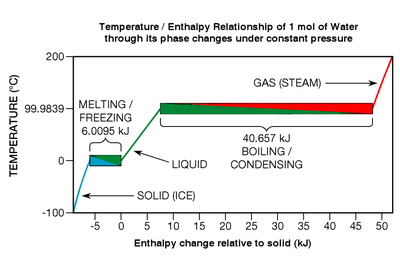
В одной конкретной термодинамической точке, точке плавления (которая составляет 0 °C в широком диапазоне давлений в случае воды), все атомы или молекулы находятся, в среднем, на максимальном энергетическом пороге, который их химические связи могут выдержать, не разрывая решетку. Химические связи являются силами «все или ничего»: они либо держатся крепко, либо разрываются; промежуточного состояния не существует. Следовательно, когда вещество находится в точке плавления, каждый джоуль добавленной тепловой энергии разрывает связи только определенного количества его атомов или молекул, ^[33] превращая их в жидкость точно такой же температуры; к поступательному движению (которое и придает веществам их температуру) не добавляется кинетическая энергия. Эффект скорее похож на попкорн : при определенной температуре дополнительная тепловая энергия не может сделать зерна горячее, пока переход (лопание) не завершится. Если процесс обратный (как при замерзании жидкости), тепловая энергия должна быть удалена из вещества.

Как указано выше, тепловая энергия, необходимая для фазового перехода, называется скрытой теплотой . В конкретных случаях плавления и замерзания она называется энтальпией плавления или теплотой плавления . Если молекулярные связи в кристаллической решетке прочны, теплота плавления может быть относительно большой, обычно в диапазоне от 6 до 30 кДж на моль для воды и большинства металлических элементов. ^[34] Если вещество является одним из одноатомных газов (которые имеют небольшую тенденцию к образованию молекулярных связей), теплота плавления более скромна, в диапазоне от 0,021 до 2,3 кДж на моль. ^[35] Условно говоря, фазовые переходы могут быть действительно энергетическими событиями. Чтобы полностью расплавить лед при 0 °C в воде при 0 °C, нужно добавить примерно в 80 раз больше тепловой энергии, чем требуется для повышения температуры той же массы жидкой воды на один градус Цельсия. Соотношения металлов еще больше, обычно в диапазоне от 400 до 1200 раз. ^[36] Фазовый переход кипения гораздо более энергичен, чем замерзание. Например, энергия, необходимая для полного кипения или испарения воды (что известно как энтальпия испарения ), примерно в 540 раз больше, чем требуется для повышения на один градус. ^[37]

Значительная энтальпия испарения воды является причиной того, что кожа человека может быть сожжена так быстро, когда пар конденсируется на ней (переходя от красного к зеленому на рис. 7  выше); водяные пары (газовая фаза) сжижаются на коже, выделяя большое количество энергии (энтальпии) в окружающую среду, включая кожу, что приводит к повреждению кожи. С другой стороны, именно поэтому кожа ощущается прохладной, когда жидкая вода на ней испаряется (процесс, который происходит при температуре ниже температуры окружающей среды по влажному термометру , которая зависит от относительной влажности ); испарение воды на коже забирает большое количество энергии из окружающей среды, включая кожу, что снижает температуру кожи. Высокоэнергетическая энтальпия испарения воды также является важным фактором, лежащим в основе того, почему солнечные покрытия для бассейнов (плавающие, изолированные одеяла, которые накрывают бассейны, когда бассейны не используются) так эффективны для снижения расходов на отопление: они предотвращают испарение. (Другими словами, получение энергии из воды при ее испарении ограничено.) Например, испарение всего 20 мм воды из бассейна глубиной 1,29 метра охлаждает воду на 8,4 °C (15,1 °F).

Внутренняя энергия

Суммарная энергия всех поступательных и внутренних движений частиц, включая энергию электронов проводимости, плюс потенциальная энергия фазовых переходов, плюс нулевая энергия ^[5] вещества составляют его внутреннюю энергию .

Рисунок 8. Когда многие химические элементы, такие как благородные газы и металлы платиновой группы , замерзают до твердого состояния — наиболее упорядоченного состояния вещества — их кристаллические структуры имеют плотноупакованную структуру . Это дает максимально возможную плотность упаковки и минимальное энергетическое состояние.

Внутренняя энергия при абсолютном нуле

По мере охлаждения вещества одновременно уменьшаются по величине различные формы внутренней энергии и связанные с ними эффекты: скрытая теплота доступных фазовых переходов высвобождается, когда вещество переходит из менее упорядоченного состояния в более упорядоченное; поступательные движения атомов и молекул уменьшаются (их кинетическая энергия или температура уменьшаются); внутренние движения молекул уменьшаются (их внутренняя энергия или температура уменьшаются); электроны проводимости (если вещество является электрическим проводником) движутся несколько медленнее; ^[38] и пиковая длина волны излучения черного тела увеличивается (энергия фотонов уменьшается). Когда частицы вещества максимально близки к полному покою и сохраняют только квантово-механическое движение, вызванное ZPE (энергией нулевой точки), вещество находится при температуре абсолютного нуля ( T  = 0).

Рисунок 9. Из-за эффектов нулевой энергии гелий при атмосферном давлении остается сверхтекучим , даже если его температура чрезвычайно близка к абсолютному нулю; он не замерзнет, ​​пока не окажется под давлением в 25 бар (около 25 атмосфер).

В то время как абсолютный ноль является точкой нулевой термодинамической температуры, а также точкой, в которой частицы, составляющие материю, имеют минимальное движение, абсолютный ноль не обязательно является точкой, в которой вещество содержит нулевую внутреннюю энергию; нужно быть очень точным с тем, что подразумевается под внутренней энергией . Часто все фазовые изменения, которые могут произойти в веществе, произойдут к тому времени, когда оно достигнет абсолютного нуля. Однако это не всегда так. В частности, при T  = 0 гелий остается жидким при комнатной температуре ( рис. 9 справа) и должен находиться под давлением не менее 25  бар (2,5  МПа ) для кристаллизации. Это связано с тем, что теплота плавления гелия (энергия, необходимая для плавления гелиевого льда) настолько мала (всего 21 джоуль на моль), что вызывающий движение эффект энергии нулевой точки достаточен, чтобы предотвратить его замерзание при более низких давлениях.

Еще одним осложнением является то, что многие твердые тела изменяют свою кристаллическую структуру на более компактную при чрезвычайно высоких давлениях (до миллионов бар или сотен гигапаскалей). Это известно как фазовые переходы твердое тело-твердое тело , при которых скрытая теплота высвобождается, когда кристаллическая решетка изменяется на более термодинамически выгодную, компактную.

Вышеуказанные сложности делают довольно громоздкими общие утверждения относительно внутренней энергии в веществах при T  = 0. Однако независимо от давления можно сказать, что при абсолютном нуле все твердые тела с кристаллической решеткой с самой низкой энергией, такие как те, которые имеют наиболее плотно упакованную компоновку (см. рис. 8 , слева вверху), содержат минимальную внутреннюю энергию, сохраняя ее только из-за постоянно присутствующего фона энергии нулевой точки. ^{[5] [39]} Можно также сказать, что для данного вещества при постоянном давлении абсолютный ноль является точкой самой низкой энтальпии (мера рабочего потенциала, которая учитывает внутреннюю энергию, давление и объем). ^[40] Наконец, все вещества при T  = 0 содержат нулевую кинетическую тепловую энергию. ^{[5] [13]}

Практические приложения термодинамической температуры

Термодинамическая температура полезна не только для ученых, она может быть полезна и для неспециалистов во многих дисциплинах, связанных с газами. Выражая переменные в абсолютных величинах и применяя закон пропорциональности температуры и давления Гей-Люссака , решения повседневных задач становятся простыми; например, вычисление того, как изменение температуры влияет на давление внутри автомобильной шины. Если шина имеет давление по манометру холода ^[41] 200  кПа , то ее абсолютное давление составляет 300 кПа. ^{[42] [43]} Комнатная температура («холодная» в терминах шин) составляет 296 К. Если температура шины на 20 °C выше (20 кельвинов), решение вычисляется как ⁠316 К/296 К⁠  = на 6,8% больше термодинамической температуры и абсолютного давления; то есть абсолютное давление 320 кПа, что соответствует избыточному давлению 220 кПа.

Связь с законом идеального газа

Термодинамическая температура тесно связана с законом идеального газа и его следствиями. Она может быть связана также со вторым законом термодинамики. Можно показать, что термодинамическая температура имеет особые свойства, и в частности, можно увидеть, что она однозначно определяется (с точностью до некоторого постоянного мультипликативного множителя), рассматривая эффективность идеализированных тепловых двигателей . Таким образом, отношение T ₂ / T ₁ двух температур T ₁ и T ₂ одинаково во всех абсолютных шкалах.

Строго говоря, температура системы хорошо определена только в том случае, если она находится в тепловом равновесии . С микроскопической точки зрения, материал находится в тепловом равновесии, если количество тепла между его отдельными частицами взаимно уничтожается. Существует множество возможных шкал температуры, полученных из различных наблюдений физических явлений.

Грубо говоря, разница температур диктует направление тепла между двумя системами таким образом, что их объединенная энергия максимально распределяется между их самыми низкими возможными состояниями. Мы называем это распределение « энтропией ». Чтобы лучше понять связь между температурой и энтропией, рассмотрим связь между теплом, работой и температурой, проиллюстрированную в тепловой машине Карно . Двигатель преобразует тепло в работу, направляя температурный градиент между источником тепла с более высокой температурой, T _H , и радиатором с более низкой температурой, T _C , через заполненный газом поршень. Работа, выполненная за цикл, равна по величине чистому потребленному теплу, которое является суммой тепла q _{H ,} потребляемого двигателем от источника высокой температуры, плюс отработанное тепло, выделяемое двигателем, q _C < 0. [ ^44] Эффективность двигателя — это работа, деленная на тепло, введенное в систему или

$${\displaystyle {\begin{aligned}{\textrm {Efficiency}}&={\frac {|w_{\text{cy}}|}{q_{\text{H}}}}={\frac {q_{\text{H}}+q_{\text{C}}}{q_{\text{H}}}}=1+{\frac {q_{\text{C}}}{q_{\text{H}}}}=1-{\frac {|q_{\text{C}}|}{|q_{\text{H}}|}}&(1)\end{aligned}}}$$

где - работа, совершаемая за цикл. Таким образом, эффективность зависит только от | q _C | / | q _H | . ${\displaystyle w_{\text{cy}}}$

Теорема Карно утверждает, что все обратимые двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Таким образом, любой обратимые тепловые двигатели, работающие между температурами T ₁ и T _2, должны иметь одинаковую эффективность, то есть эффективность является функцией только температур $${\displaystyle {\begin{aligned}{\frac {|q_{\text{C}}|}{|q_{\text{H}}|}}&=f(T_{\text{H}},T_{\text{C}}).&(2)\end{aligned}}}$$

Кроме того, обратимый тепловой двигатель, работающий между парой тепловых резервуаров при температурах T ₁ и T _3, должен иметь такую ​​же эффективность, как и двигатель, состоящий из двух циклов, один между T ₁ и другой (промежуточной) температурой T ₂ , а второй между T ₂ и T ₃ . Если бы это было не так, то энергия (в форме q ) тратилась бы впустую или приобреталась, что приводило бы к разным общим КПД каждый раз, когда цикл разделяется на составные циклы; очевидно, что цикл может состоять из любого количества меньших циклов в качестве выбора конструкции двигателя, и любой обратимый двигатель между тем же резервуаром при T ₁ и T ₃ должен быть одинаково эффективным независимо от конструкции двигателя.

Если мы выберем двигатели таким образом, что работа, выполняемая однотактным и двухтактным двигателями, будет одинаковой, то КПД каждого теплового двигателя запишется следующим образом. $${\displaystyle {\begin{aligned}\eta _{1}&=1-{\frac {|q_{3}|}{|q_{1}|}}&=1-f(T_{1},T_{3})\\\eta _{2}&=1-{\frac {|q_{2}|}{|q_{1}|}}&=1-f(T_{1},T_{2})\\\eta _{3}&=1-{\frac {|q_{3}|}{|q_{2}|}}&=1-f(T_{2},T_{3})\end{aligned}}}$$

Здесь двигатель 1 является однотактным, а двигатели 2 и 3 составляют двухтактный двигатель, в котором имеется промежуточный резервуар при T ₂ . Мы также использовали тот факт, что тепло проходит через промежуточный тепловой резервуар при , не теряя своей энергии. (Т.е. не теряется при прохождении через резервуар при .) Этот факт можно доказать следующим образом. ${\displaystyle q_{2}}$ ${\displaystyle T_{2}}$ ${\displaystyle q_{2}}$ ${\displaystyle T_{2}}$ $${\displaystyle {\begin{aligned}{{\eta }_{2}}&=1-{\frac {|{{q}_{2}}|}{|{{q}_{1}}|}}\to |{{w}_{2}}|=|{{q}_{1}}|-|{{q}_{2}}|,\\{{\eta }_{3}}&=1-{\frac {|{{q}_{3}}|}{|{{q}_{2}}^{*}|}}\to |{{w}_{3}}|=|{{q}_{2}}^{*}|-|{{q}_{3}}|,\\|{{w}_{2}}|+|{{w}_{3}}|&=(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|),\\{{\eta }_{1}}&=1-{\frac {|{{q}_{3}}|}{|{{q}_{1}}|}}={\frac {(|{{w}_{2}}|+|{{w}_{3}}|)}{|{{q}_{1}}|}}={\frac {(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|)}{|{{q}_{1}}|}}.\\\end{aligned}}}$$

Для обеспечения согласованности последнего уравнения тепло, переданное от двигателя 2 к промежуточному резервуару, должно быть равно теплу, переданному от резервуара к двигателю 3. ${\displaystyle q_{2}}$ ${\displaystyle q_{2}^{*}}$

При таком понимании q ₁ , q ₂ и q ₃ , математически, $${\displaystyle f(T_{1},T_{3})={\frac {|q_{3}|}{|q_{1}|}}={\frac {|q_{2}||q_{3}|}{|q_{1}||q_{2}|}}=f(T_{1},T_{2})f(T_{2},T_{3}).}$$

Но поскольку первая функция не является функцией T ₂ , произведение последних двух функций должно привести к удалению T ₂ как переменной. Поэтому единственный способ — определить функцию f следующим образом: и так, чтобы $${\displaystyle f(T_{1},T_{2})={\frac {g(T_{2})}{g(T_{1})}}}$$ $${\displaystyle f(T_{2},T_{3})={\frac {g(T_{3})}{g(T_{2})}}}$$ $${\displaystyle f(T_{1},T_{3})={\frac {g(T_{3})}{g(T_{1})}}={\frac {|q_{3}|}{|q_{1}|}}.}$$

То есть отношение теплообмена является функцией соответствующих температур, при которых они происходят. Мы можем выбрать любую монотонную функцию для нашего ; ^[45] это вопрос удобства и соглашения, что мы выбираем . Выбрав затем одну фиксированную опорную температуру (т.е. тройную точку воды), мы устанавливаем термодинамическую температурную шкалу. ${\displaystyle g(T)}$ ${\displaystyle g(T)=T}$

Такое определение совпадает с определением идеального газа; также именно это определение термодинамической температуры позволяет нам представить КПД Карно в терминах T _H и T _C , и, следовательно, вывести, что (полный) цикл Карно является изэнтропическим: $${\displaystyle {\frac {|q_{\text{C}}|}{|q_{\text{H}}|}}=f(T_{\text{H}},T_{\text{C}})={\frac {T_{\text{C}}}{T_{\text{H}}}}.\ \ \ \ \ \ \ \ \ \ \ (3)}$$

Подставляя это обратно в нашу первую формулу эффективности, получаем зависимость в терминах температуры: $${\displaystyle {\textrm {Efficiency}}=1+{\frac {q_{\text{C}}}{q_{\text{H}}}}=1-{\frac {|q_{\text{C}}|}{|q_{\text{H}}|}}=1-{\frac {T_{\text{C}}}{T_{\text{H}}}}.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)}$$

Обратите внимание, что при T _C = 0 эффективность составляет 100%, а при T _C < 0 эффективность становится больше 100% , что нереально. Вычитание 1 из правой части уравнения (4) и средней части дает и, таким образом, ^{[46] [44]} ${\displaystyle {\frac {q_{\text{C}}}{q_{\text{H}}}}=-{\frac {T_{\text{C}}}{T_{\text{H}}}}}$ $${\displaystyle {\frac {q_{\text{H}}}{T_{\text{H}}}}+{\frac {q_{\text{C}}}{T_{\text{C}}}}=0.}$$

Обобщением этого уравнения является теорема Клаузиуса , которая предполагает существование функции состояния (т. е. функции, которая зависит только от состояния системы, а не от того, как она достигла этого состояния), определяемой (с точностью до аддитивной константы) как ${\displaystyle S}$

$${\displaystyle {\begin{aligned}dS&={\frac {dq_{\mathrm {rev} }}{T}}&(5)\end{aligned}}}$$

где нижний индекс rev указывает на перенос тепла в обратимом процессе. Функция — это энтропия системы, упомянутая ранее, а изменение вокруг любого цикла равно нулю (как это необходимо для любой функции состояния). Уравнение 5 можно переставить, чтобы получить альтернативное определение температуры в терминах энтропии и тепла (чтобы избежать логической петли, мы должны сначала определить энтропию через статистическую механику): ${\displaystyle S}$ ${\displaystyle S}$ $${\displaystyle T={\frac {dq_{\mathrm {rev} }}{dS}}.}$$

Для системы с постоянным объемом (то есть без механической работы ), в которой энтропия является функцией ее внутренней энергии , термодинамическая температура, следовательно, определяется выражением, так что обратная величина термодинамической температуры является скоростью изменения энтропии по отношению к внутренней энергии при постоянном объеме. ${\displaystyle W}$ ${\displaystyle S}$ ${\displaystyle S(E)}$ ${\displaystyle E}$ ${\displaystyle dE=dq_{rev}}$ ${\displaystyle T}$ $${\displaystyle {\frac {1}{T}}={\frac {dS}{dE}},}$$

История

Гийом Амонтонс

Гийом Амонтон (1663–1705) опубликовал две статьи в 1702 и 1703 годах, которые можно использовать для признания его первым исследователем, выведшим существование фундаментальной (термодинамической) температурной шкалы с абсолютным нулем. Он сделал это открытие, пытаясь усовершенствовать воздушные термометры, использовавшиеся в то время. Его J-образные термометры состояли из ртутного столба, который поддерживался фиксированной массой воздуха, заключенного в чувствительной части термометра. С точки зрения термодинамики, его термометры основывались на соотношении объема и температуры газа под постоянным давлением. Его измерения точки кипения воды и точки плавления льда показали, что независимо от массы воздуха, заключенного в его термометрах, или веса ртути, поддерживаемой воздухом, уменьшение объема воздуха в точке замерзания всегда было одинаковым. Это наблюдение привело его к выводу, что достаточное снижение температуры уменьшит объем воздуха до нуля. Фактически, его расчеты предсказывали, что абсолютный ноль был эквивалентен −240 °C — всего на 33,15 градуса меньше истинного значения −273,15 °C. Открытие Амонтоном однозначного соотношения между абсолютной температурой и абсолютным давлением было переоткрыто столетие спустя и популяризировано в научном сообществе Жозефом Луи Гей-Люссаком . Сегодня этот принцип термодинамики широко известен как закон Гей-Люссака, но также известен как закон Амонтона .

Андерс Цельсий

В 1742 году Андерс Цельсий (1701–1744) создал «обратную» версию современной температурной шкалы Цельсия. В оригинальной шкале Цельсия ноль представлял точку кипения воды, а 100 — точку таяния льда. В своей статье « Наблюдения за двумя постоянными градусами на термометре» он рассказал о своих экспериментах, показывающих, что точка таяния льда фактически не зависит от давления. Он также с удивительной точностью определил, как точка кипения воды изменяется в зависимости от атмосферного давления. Он предположил, что ноль на его температурной шкале (точка кипения воды) будет откалиброван по среднему барометрическому давлению на среднем уровне моря.

Карл Линней

Одновременно со смертью Андерса Цельсия в 1744 году ботаник Карл Линней (1707–1778) фактически перевернул ^{[47] [48] [ необходима полная цитата ]} шкалу Цельсия, получив свой первый термометр со шкалой, где ноль представлял точку таяния льда, а 100 представляло точку кипения воды. Изготовленный на заказ термометр Линнея для использования в его теплицах был изготовлен Даниэлем Экстрёмом, ведущим производителем научных приборов в Швеции в то время. В течение следующих 204 лет научные и термометрические сообщества во всем мире называли эту шкалу шкалой Цельсия . Температуры по шкале Цельсия часто сообщались просто в градусах или, когда требовалась большая конкретность, в градусах Цельсия . Символом значений температуры по этой шкале был °C (в нескольких форматах на протяжении многих лет). Поскольку термин «стоградус» был также французским названием единицы измерения угла (одна сотая часть прямого угла) и имел схожее значение в других языках, термин « сотенный градус » использовался, когда международные органы по стандартизации, такие как Международное бюро мер и весов (BIPM), требовали очень точного, недвусмысленного языка. 9-я Генеральная конференция по мерам и весам (CGPM) и CIPM ( Международный комитет по мерам и весам) официально приняли ^[49] градус Цельсия (символ: °C) в 1948 году.

Иоганн Генрих Ламберт

В своей книге Pyrometrie (1777) ^[50] , завершенной за четыре месяца до его смерти, Иоганн Генрих Ламберт (1728–1777), иногда неправильно называемый Йозефом Ламбертом, предложил абсолютную температурную шкалу, основанную на соотношении давления и температуры фиксированного объема газа. Это отличается от соотношения объема и температуры газа при постоянном давлении, которое Гийом Амонтон открыл 75 лет назад. Ламберт утверждал, что абсолютный ноль — это точка, в которой простая прямолинейная экстраполяция достигает нулевого давления газа и равна −270 °C.

Жак Александр Сезар Шарль

Несмотря на работу Гийома Амонтона 85 лет назад, Жаку Александру Сезару Шарлю (1746–1823) часто приписывают открытие (около 1787 г.), но не публикацию, того, что объем газа под постоянным давлением пропорционален его абсолютной температуре. Формула, которую он создал, была V ₁ / T ₁ = V ₂ / T ₂ .

Жозеф Луи Гей-Люссак

Жозеф Луи Гей-Люссак (1778–1850) опубликовал работу в 1802 году (признавая неопубликованные лабораторные заметки Жака Шарля пятнадцатью годами ранее), описывающую, как объем газа под постоянным давлением изменяется линейно с его абсолютной (термодинамической) температурой. Это поведение называется законом Шарля и является одним из газовых законов . Его формулы являются первыми известными, использующими число 273 для коэффициента расширения газа относительно точки плавления льда (указывая, что абсолютный ноль был эквивалентен −273 °C).

Лорд Кельвин

Уильям Томсон (1824–1907), также известный как лорд Кельвин, писал в своей статье 1848 года «Об абсолютной термометрической шкале» ^[51] о необходимости шкалы, в которой бесконечный холод (абсолютный ноль) был бы нулевой точкой шкалы, и которая использовала бы градус Цельсия в качестве единицы приращения. Как и Гей-Люссак, Томсон вычислил, что абсолютный ноль был эквивалентен −273 °C на воздушных термометрах того времени. Эта абсолютная шкала известна сегодня как термодинамическая температурная шкала Кельвина. Значение Томсона −273 было получено из 0,00366, что было принятым коэффициентом расширения газа на градус Цельсия относительно точки замерзания. Обратное значение −0,00366, выраженное с пятью значащими цифрами, равно −273,22 °C, что удивительно близко к истинному значению −273,15 °C.

В своей статье он предложил определять температуру с помощью идеализированных тепловых машин. В деталях он предложил, что, учитывая три тепловых резервуара при температурах , если две обратимые тепловые машины ( двигатель Карно ), одна из которых работает между , а другая между , могут производить одинаковое количество механической работы , пропуская одинаковое количество тепла , то определите . ${\displaystyle T_{A},T_{B},T_{C}}$ ${\displaystyle T_{A},T_{B}}$ ${\displaystyle T_{B},T_{C}}$ ${\displaystyle W}$ ${\displaystyle Q}$ ${\displaystyle T_{A}-T_{B}=T_{B}-T_{C}}$

Обратите внимание, что, как и Карно, Кельвин работал, исходя из предположения, что тепло сохраняется («превращение тепла (или теплоты) в механический эффект, вероятно, невозможно»), и если тепло поступает в тепловую машину, то тепло должно и выделяться. ^[52] ${\displaystyle Q}$ ${\displaystyle Q}$

Кельвин, поняв после экспериментов Джоуля, что тепло не является сохраняющейся величиной, а преобразуется с помощью механической работы, модифицировал свою шкалу в работе 1851 года « Изложение теории Карно о движущей силе тепла» . В этой работе он дал следующее определение: ^[53]

Даны два тепловых резервуара и работающий между ними обратимый тепловой двигатель, так что если во время цикла двигателя тепло поступает в двигатель и тепло выходит из двигателя, то . ${\displaystyle T_{A},T_{B}}$ ${\displaystyle Q_{A}}$ ${\displaystyle Q_{B}}$ ${\displaystyle {\frac {T_{A}}{T_{B}}}={\frac {Q_{A}}{Q_{B}}}}$

Приведенное выше определение фиксирует соотношения между абсолютными температурами, но не фиксирует шкалу для абсолютной температуры. Для шкалы Томсон предложил использовать градус Цельсия, то есть интервал между точкой замерзания и точкой кипения воды. ${\displaystyle {\frac {1}{100}}}$

Маккорн Рэнкин

В 1859 году Маккорн Ранкин (1820–1872) предложил термодинамическую температурную шкалу, похожую на шкалу Уильяма Томсона, но в которой единицей приращения был градус Фаренгейта , то есть интервал между точкой замерзания и точкой кипения воды. Эта абсолютная шкала сегодня известна как термодинамическая температурная шкала Ранкина . ${\displaystyle {\frac {1}{180}}}$

Людвиг Больцман

Людвиг Больцман (1844–1906) внес большой вклад в термодинамику между 1877 и 1884 годами, поняв роль, которую играли кинетика частиц и излучение черного тела. Его имя теперь связано с несколькими формулами, используемыми сегодня в термодинамике.

Эксперименты по газовой термометрии ^{[ кем? ],} тщательно откалиброванные по температуре плавления льда и температуре кипения воды, показали в 1930-х годах, что абсолютный ноль эквивалентен температуре -273,15 °C.

Резолюция 3 ^[54] 9-й Генеральной конференции по мерам и весам (CGPM) в 1948 году зафиксировала тройную точку воды точно на 0,01 °C. В то время тройная точка все еще не имела формального определения для ее эквивалентного значения в кельвинах, которое, как было заявлено в резолюции, «будет зафиксировано позднее». Подразумевается, что если значение абсолютного нуля, измеренное в 1930-х годах, действительно составляло -273,15 °C, то тройная точка воды (0,01 °C) была эквивалентна 273,16 K. Кроме того, как Международный комитет по мерам и весам (CIPM), так и CGPM официально приняли ^[55] название Цельсий для градуса Цельсия и температурной шкалы Цельсия . ^[58]

Резолюция 3 ^[59] 10-й ГКМВ в 1954 году дала шкале Кельвина ее современное определение, выбрав тройную точку воды в качестве ее верхней определяющей точки (без изменения абсолютного нуля в качестве нулевой точки) и присвоив ей температуру точно 273,16 кельвина (что на самом деле было написано в то время как 273,16 градуса Кельвина ). Это, в сочетании с Резолюцией 3 9-й ГКМВ, имело эффект определения абсолютного нуля как точно ноль кельвинов и −273,15 °C.

Резолюция 3 ^[60] 13-й ГКМВ в 1967/1968 гг. переименовала единицу приращения термодинамической температуры в кельвин , символ К, заменив абсолютный градус , символ °К. Кроме того, посчитав полезным более четко определить величину единицы приращения, 13-я ГКМВ также постановила в Резолюции 4 ^[61] , что «Кельвин, единица термодинамической температуры, составляет часть 1/273,16 термодинамической температуры тройной точки воды».

В 2005 году МКМВ подтвердил ^[62] , что для целей определения температуры тройной точки воды определение термодинамической шкалы температур Кельвина будет относиться к воде, имеющей изотопный состав, определяемый как точно соответствующий номинальной спецификации Венского стандарта средней океанической воды .

В ноябре 2018 года 26-я Генеральная конференция по мерам и весам (CGPM) изменила определение градуса Кельвина, зафиксировав постоянную Больцмана следующим образом:1,380 649 × 10−23 при выражении в единицах Дж/К. ^Это изменение (и другие изменения в определении единиц СИ) вступило в силу в 144-ю годовщину Метрической конвенции, 20 мая 2019 года.

Смотрите также

• Категория:Термодинамика
• Абсолютный ноль
• температура Хагедорна
• Адиабатический процесс
• постоянная Больцмана
• Тепловая машина Карно
• Перевод шкал температуры
• Эффективность преобразования энергии
• Энтальпия
  • Энтальпия плавления
  • Энтальпия испарения
• Энтропия
• Теорема о равнораспределении
• по Фаренгейту
• Первый закон термодинамики
• Замораживание
• Газовые законы
• Международная система величин
• Международная температурная шкала 1990 года (МТШ-90)
• Закон идеального газа
• Кельвин
• Законы термодинамики
• Распределение Максвелла-Больцмана
• Порядки величин (температура)
• Фазовый переход
• Закон Планка об излучении черного тела
• шкала Рэнкина
• Удельная теплоемкость
• Температура
• Тепловое излучение
• Термодинамическая бета
• Термодинамические уравнения
• Термодинамическое равновесие
• Термодинамика
• Хронология развития технологии тепловых двигателей
• Хронология развития технологий измерения температуры и давления
• Тройная точка

Примечания

В следующих примечаниях, везде, где числовые равенства показаны в краткой форме , например:1,854 87 (14) × 10 ⁴³ , две цифры в скобках обозначают неопределенность при 1-σ (1 стандартное отклонение , уровень достоверности 68%) в двух младших цифрах значащей части .

1. CODATA Значение: постоянная Больцмана . Справочник NIST по константам, единицам и неопределенности . Национальный институт стандартов и технологий .
2. Университет штата Джорджия, Проект Гиперфизики, «Равномерное распределение энергии»
3. Рэнкин, У. Дж. М., «Руководство по паровой машине и другим первичным двигателям», Richard Griffin and Co., Лондон (1859), стр. 306–307.
4. Уильям Томсон, 1-й барон Кельвин , «Жара», Адам и Чарльз Блэк, Эдинбург (1880), стр. 39.

5. 

   Связь абсолютного нуля с энергией нулевой точки

   В то время как ученые достигают температур, все более близких к абсолютному нулю , они не могут полностью достичь состояния нулевой температуры. Однако, даже если ученые могли бы удалить всю кинетическую тепловую энергию из материи, квантово-механическая энергия нулевой точки (ZPE) вызывает движение частиц, которое никогда не может быть устранено. Encyclopædia Britannica Online определяет энергию нулевой точки как «колебательную энергию, которую молекулы сохраняют даже при абсолютном нуле температуры». ZPE является результатом всепроникающих энергетических полей в вакууме между фундаментальными частицами природы; она отвечает за эффект Казимира и другие явления. См. Zero Point Energy и Zero Point Field . См. также Solid Helium Архивировано 2008-02-12 в Wayback Machine физическим факультетом Университета Альберты, чтобы узнать больше о влиянии ZPE на конденсаты Бозе-Эйнштейна гелия.

   Хотя абсолютный ноль ( T = 0 ) не является состоянием нулевого молекулярного движения, это точка  нулевой температуры и, в соответствии с постоянной Больцмана, также точка нулевой кинетической энергии частиц и нулевой кинетической скорости.Чтобы понять, как атомы могут иметь нулевую кинетическую скорость и одновременно вибрировать из-за ZPE, рассмотрим следующий мысленный эксперимент: два атома гелия при T = 0 в невесомости аккуратно размещены и наблюдаются на среднем расстоянии между ними в 620  пм (зазор в десять атомных диаметров). Это «среднее» расстояние, поскольку ZPE заставляет их толкаться относительно их фиксированных положений. Затем один атом получает кинетический толчок точно в 83 йоктокельвина (1 yK =1 × 10−24  K ). Это делается таким образом, что вектор скорости этого атома направляется на другой атом. При 83 yK кинетической энергии между ними зазор в 620 пм через их общий барицентр закроется со скоростью 719 пм/с, и они столкнутся через 0,862 секунды. Это та же скорость, что показана на ^{анимации} рис. 1 выше. До получения кинетического толчка оба атома T = 0 имели нулевую кинетическую энергию и нулевую кинетическую скорость, поскольку они могли сохраняться в этом состоянии и относительной ориентации неопределенно долго, даже если оба подталкивались ZPE. При T = 0 кинетическая энергия недоступна для передачи другим системам.

   Обратите внимание также, что абсолютный ноль служит базовой линией, на которой основываются термодинамика и ее уравнения , поскольку они имеют дело с обменом тепловой энергией между « системами » (множеством частиц и полей, моделируемых как среднее). Соответственно, можно исследовать движение частиц, вызванное ZPE, в системе, которая находится при абсолютном нуле, но из такой системы никогда не может быть чистого оттока тепловой энергии. Кроме того, пиковая длина волны излучения черного тела смещается к бесконечности при абсолютном нуле; действительно, пик больше не существует, и фотоны черного тела больше не могут вырваться. Однако из-за ZPE виртуальные фотоны все еще испускаются при T = 0. Такие фотоны называются «виртуальными», потому что их нельзя перехватить и наблюдать. Кроме того, это излучение нулевой точки имеет уникальный спектр нулевой точки . Однако, даже если система T = 0 испускает нулевое излучение, никакого чистого потока тепла Q из такой системы не может возникнуть, потому что если окружающая среда имеет температуру выше T = 0 , тепло будет течь внутрь, а если окружающая среда имеет температуру ' T = 0 , будет равный поток излучения ZP как внутрь, так и наружу. Подобное равновесие Q существует при T = 0 с вызванным ZPE спонтанным излучением фотонов (которое в этом контексте правильнее называть стимулированным излучением). График вверху справа иллюстрирует связь абсолютного нуля с энергией нулевой точки. График также помогает понять, как энергия нулевой точки получила свое название: это колебательная энергия, которую материя сохраняет в точке нулевого кельвина . Вывод классического электромагнитного спектра нулевого излучения с помощью классической термодинамической операции, включающей силы Ван-дер-Ваальса, Daniel C. Cole, Physical Review A, 42 (1990) 1847.

6. "Брошюра SI, раздел 2.1.1.5". Международное бюро мер и весов . Архивировано из оригинала 26 сентября 2007 г. Получено 9 мая 2008 г.
7. Newell, DB; Cabiati, F; Fischer, J; Fujii, K; Karshenboim, SG; Margolis, HS; de Mirandés, E; Mohr, PJ; Nez, F; Pachucki, K; Quinn, TJ; Taylor, BN; Wang, M; Wood, BM; Zhang, Z; et al. (Комитет по данным для науки и технологий (CODATA), целевая группа по фундаментальным константам) (29 января 2018 г.). "Значения CODATA 2017 h, e, k и NA для пересмотра SI". Metrologia . 55 (1): L13–L16. Bibcode : 2018Metro..55L..13N. doi : 10.1088/1681-7575/aa950a .
8. "SI Redefinition – Kelvin: Boltzmann Constant". Национальный институт стандартов и технологий . Архивировано из оригинала 1 июля 2020 года . Получено 13 декабря 2020 года .
9. "Акустическая термометрия". Национальный институт стандартов и технологий . Архивировано из оригинала 23 сентября 2020 г. Получено 13 декабря 2020 г.
10. При нерелятивистских температурах менее 30 ГК для расчета скорости частиц достаточно классической механики . При 30 ГК отдельные нейтроны (составная часть нейтронных звезд и один из немногих материалов во Вселенной с температурами в этом диапазоне) имеют 1,0042 γ (гамма или фактор Лоренца ). Таким образом, классическая ньютоновская формула для кинетической энергии имеет ошибку менее половины процента для температур менее 30 ГК.
11. Даже воздух комнатной температуры имеет среднюю молекулярную поступательную скорость (не векторно-изолированную скорость) 1822 км/час. Это относительно быстро для чего-то размером с молекулу, учитывая, что есть примерно2,42 × 10 ¹⁶ из них, сгруппированных в один кубический миллиметр. Предположения: Средний молекулярный вес влажного воздуха = 28,838 г/моль и T = 296,15 K. Основные переменные предположения: Высота 194 метра над средним уровнем моря (мировая медианная высота проживания человека), температура в помещении 23 °C, точка росы 9 °C (относительная влажность 40,85%) и  барометрическое давление с поправкой на уровень моря 760 мм рт. ст. (101 кПа).
12. Кастберг, А.; и др. (27 февраля 1995 г.). «Адиабатическое охлаждение цезия до 700 нК в оптической решетке». Physical Review Letters . 74 (9): 1542–1545. Bibcode :1995PhRvL..74.1542K. doi :10.1103/PhysRevLett.74.1542. PMID  10059055.Рекордно низкая температура 450  пК в конденсате Бозе-Эйнштейна атомов натрия (достигнутая А. Э. Леанхардтом и др . из Массачусетского технологического института ){{cn|{{subst:DATE}} соответствует средней векторно-изолированной скорости атома 0,4 мм/с и средней скорости атома 0,7 мм/с.
13. Скорость поступательного движения атомов и молекул рассчитывается на основе термодинамической температуры следующим образом: где $${\displaystyle {\tilde {v}}={\sqrt {\frac {{\frac {k_{\text{B}}}{2}}\cdot T}{\frac {m}{2}}}}}$$
    • ${\textstyle {\tilde {v}}}$- векторно-изолированная средняя скорость поступательного движения частицы в м/с
    • k _B ( постоянная Больцмана ) =1,380 649 × 10−23 Дж ^/  К
    • T — термодинамическая температура в кельвинах.
    • m — молекулярная масса вещества в кг/частица
    В приведенной выше формуле молекулярная масса m в кг/частица представляет собой частное от деления молярной массы вещества (также известной как атомный вес , атомная масса , относительная атомная масса и унифицированные атомные единицы массы ) в г / моль или дальтонах на6,022 140 76 × 10 ²⁶ (что равно постоянной Авогадро, умноженной на тысячу). Для двухатомных молекул, таких как H 2 , N 2 и O 2 , умножьте атомный вес на два, прежде чем подставлять его в приведенную выше формулу. Средняя скорость (не векторно-изолированная скорость) атома или молекулы по любой произвольной траектории вычисляется следующим образом: где — средняя скорость поступательного движения частиц в м/с. Средняя энергия поступательных движений составляющих вещество частиц коррелирует с их средней скоростью , а не со скоростью. Таким образом, подставляя вместо v классическую формулу для кинетической энергии, E _k = ⁠ $${\displaystyle {\tilde {s}}={\tilde {v}}\cdot {\sqrt {3}}}$$ ${\textstyle {\tilde {s}}}$ ${\textstyle {\tilde {s}}}$1/2⁠ mv ² дает точно такое же значение, как и E _mean = 3/2 k _B T (как показано в § Природа кинетической энергии, поступательного движения и температуры). Постоянная Больцмана и связанные с ней формулы устанавливают, что абсолютный ноль является точкой как нулевой кинетической энергии движения частицы, так и нулевой кинетической скорости (см. также Примечание 1 выше).
14. Одна триллионная кельвина относится к одному кельвину так же, как толщина двух листов кухонной алюминиевой фольги (0,04 мм) относится к расстоянию вокруг Земли по экватору.
15. Внутренние степени свободы молекул заставляют их внешние поверхности вибрировать и также могут производить общие вращательные движения (что можно сравнить с покачиванием и вращением в остальном неподвижного водяного шарика). Если рассмотреть отдельную молекулу, ударяющуюся о стенку контейнера, то часть кинетической энергии, переносимой во внутренних степенях свободы молекулы, может конструктивно добавиться к ее поступательному движению в момент столкновения, и дополнительная кинетическая энергия будет передана стенке контейнера. Это вызовет дополнительный, локализованный, импульсный вклад в среднее давление на контейнер. Однако, поскольку внутренние движения молекул случайны, они имеют равную вероятность деструктивно помешать поступательному движению во время столкновения со стенками контейнера или другой молекулой. Усредненные по любому объемному количеству газа, внутренние тепловые движения молекул имеют нулевое чистое влияние на температуру, давление или объем газа. Внутренние степени свободы молекул просто предоставляют дополнительные места, где хранится кинетическая энергия. Именно поэтому молекулярные газы имеют большую удельную внутреннюю емкость, чем одноатомные газы (где для достижения заданного повышения температуры необходимо приложить дополнительную внутреннюю энергию).
16. При измерении при постоянном объеме, поскольку при измерении при постоянном давлении необходимо выполнить разное количество работы. C _v H азота (100 кПа, 20 °C) равно20,8 Дж моль ^–1 ⋅К ^–1 по сравнению с одноатомными газами, что равно 12,4717 Дж моль ^–1  К ^–1 . Freeman, WH "Часть 3: Изменение". Физическая химия (PDF) . Упражнение 21.20b, стр. 787. Архивировано из оригинала (PDF) 2007-09-27.См. также Nave, R. "Молярная удельная теплоемкость газов". HyperPhysics . Университет штата Джорджия.
17. Скорость , с которой тепловая энергия выравнивается по всему объему газа, очень велика. Однако, поскольку газы имеют чрезвычайно низкую плотность по сравнению с твердыми телами, тепловой поток (тепловая мощность, проходящая через площадь) через газы сравнительно низок. Вот почему мертвые воздушные пространства в многокамерных окнах обладают изолирующими свойствами.
18. Алмаз является заметным исключением. Высококвантованные моды фононных колебаний происходят в его жесткой кристаллической решетке. Поэтому алмаз не только имеет исключительно низкую удельную теплоемкость , но и исключительно высокую теплопроводность .
19. Корреляция составляет 752 (Вт⋅м ⁻¹ ⋅К ⁻¹ )/(МС⋅см), σ  = 81, в диапазоне проводимости 7:1. Значение и стандартное отклонение основаны на данных для Ag, Cu, Au, Al, Ca, Be, Mg, Rh, Ir, Zn, Co, Ni, Os, Fe, Pa, Pt и Sn. Данные из CRC Handbook of Chemistry and Physics , 1st Student Edition.
20. Приведенные длины волн излучения соответствуют истинно черным телам в равновесии. В этой таблице только солнце соответствует этому критерию. CODATA рекомендует значение2,897 771 955 ... × 10 ⁻³  м⋅К используется для константы закона смещения Вина b .
21. Рекордно низкая температура 450 ±80 пК в конденсате Бозе-Эйнштейна (БЭК) атомов натрия ( ²³ Na) была достигнута в 2003 году исследователями из Массачусетского технологического института . Leanhardt, AE; et al. (12 сентября 2003 г.). "Охлаждение конденсатов Бозе-Эйнштейна ниже 500 пикокельвинов". Science . 301 (5639): 1515. Bibcode :2003Sci...301.1513L. doi :10.1126/science.1088827. PMID  12970559.Тепловая скорость атомов в среднем составила около 0,4 мм/с. Длина волны излучения абсолютно черного тела этого рекорда составляет 6400 километров, что примерно равно радиусу Земли.
22. Пиковая длина волны излучения 2,897 77 м соответствует частоте 103,456 МГц.
23. «Резолюция B3 о рекомендуемых номинальных константах преобразования для выбранных солнечных и планетарных свойств» (PDF) . 2015.
24. Hertel, Ingolf V.; Schulz, Claus-Peter (2014-10-24). Атомы, молекулы и оптическая физика 1: Атомы и спектроскопия. Springer. стр. 35. ISBN 978-3-642-54322-7.
25. Виньола, Франк; Михальски, Джозеф; Стоффель, Томас (2019-07-30). Измерения солнечного и инфракрасного излучения (2-е изд.). CRC Press. стр. главы 2.1, 2.2. ISBN 978-1-351-60020-0.
26. "Информационный листок о Солнце". Координированный архив Космического научного центра НАСА . Получено 27 августа 2023 г.
27. Значение 350 МК — это максимальная пиковая температура термоядерного топлива в термоядерном оружии конфигурации Теллера–Улама (обычно известном как «водородная бомба»). Пиковые температуры в ядрах бомб деления типа Gadget (обычно известных как «атомная бомба») находятся в диапазоне от 50 до 100 МК. «Часто задаваемые вопросы о ядерном оружии». 3.2.5 Материя при высоких температурах.^{[ необходима полная ссылка ]} Все справочные данные были получены из общедоступных источников.
28. Пиковая температура для большого количества вещества была достигнута с помощью импульсной машины, используемой в экспериментах по физике термоядерного синтеза. Термин «большое количество» проводит различие от столкновений в ускорителях частиц, где высокая «температура» применяется только к осколкам двух субатомных частиц или ядер в любой данный момент. Температура >2 ГК была достигнута в течение периода около десяти наносекунд во время «выстрела Z1137». Фактически, ионы железа и марганца в плазме имели в среднем 3,58 ± 0,41 ГК (309 ± 35 кэВ) в течение 3 нс (нс 112–115). Haines, MG; et al. (2006). «Вязкий нагрев ионов в магнитогидродинамически нестабильном Z-пинче при температуре более 2 × 10 ⁹ Кельвинов». Physical Review Letters . 96 (7): 075003. Библиографический код : 2006PhRvL..96g5003H. doi : 10.1103/PhysRevLett.96.075003. PMID  16606100. № 075003.Для пресс-релиза этой статьи см. "Sandia's Z machine overs two billion degrees Kelvin". Sandia. 8 марта 2006 г. Архивировано из оригинала 2006-07-02.
29. Температура ядра звезды с большой массой (>8–11 масс Солнца) после того, как она покидает главную последовательность на диаграмме Герцшпрунга–Рассела и начинает альфа-процесс (который длится один день) слияния кремния-28 в более тяжелые элементы в следующих этапах: сера-32 → аргон-36 → кальций-40 → титан-44 → хром-48 → железо-52 → никель-56. Через несколько минут после завершения последовательности звезда взрывается как сверхновая типа II .
30. На основе компьютерной модели, которая предсказывала пиковую внутреннюю температуру 30 МэВ (350 ГК) во время слияния двойной нейтронной звездной системы (что производит гамма-всплеск). Нейтронные звезды в модели имели 1,2 и 1,6 солнечных масс соответственно, были примерно 20 км в диаметре и вращались вокруг своего барицентра (общего центра масс) с частотой около 390 Гц в течение последних нескольких миллисекунд перед тем, как они полностью слились. Часть 350 ГК представляла собой небольшой объем, расположенный в развивающемся общем ядре пары, и менялась от примерно 1 до 7 км в поперечнике в течение промежутка времени около 5 мс. Представьте себе два объекта размером с город невообразимой плотности, вращающихся друг вокруг друга на той же частоте, что и музыкальная нота G4 (28-я белая клавиша на фортепиано). При 350 ГК средний нейтрон имеет вибрационную скорость, составляющую 30% скорости света, и релятивистскую массу, на 5% превышающую его массу покоя. Охслин, Р.; Янка, Х.-Т. (2006). «Формирование тора при слияниях нейтронных звезд и хорошо локализованных коротких гамма-всплесках». Monthly Notices of the Royal Astronomical Society . 368 (4): 1489–1499. arXiv : astro-ph/0507099v2 . Bibcode : 2006MNRAS.368.1489O. doi : 10.1111/j.1365-2966.2006.10238.x . S2CID  15036056.Для краткого обзора см. «Короткие гамма-всплески: предсмертные муки сливающихся нейтронных звезд». Институт астрофизики им. Макса Планка . Получено 24 сентября 2024 г.
31. Баттерсби, Стивен (2 марта 2011 г.). «Восемь крайностей: самая горячая вещь во Вселенной». New Scientist . Хотя детали этого процесса в настоящее время неизвестны, он должен включать огненный шар релятивистских частиц, нагретых до температуры в районе триллиона кельвинов.
32. "Как физики изучают частицы?". ЦЕРН. Архивировано из оригинала 2007-10-11.
33. Энтальпия плавления воды (0 °C, 101,325 кПа) равна0,062 284  эВ  на молекулу, поэтому добавление одного джоуля тепловой энергии к водяному льду при температуре 0 °C вызывает1,0021 × 1020 молекул воды ^{необходимо} , чтобы оторваться от кристаллической решетки и стать жидкостью.
34. Энтальпия плавления воды равна6,0095 кДж⋅моль ⁻¹ K ⁻¹ (0 °C, 101,325 кПа). Чаплин, Мартин. "Свойства воды (включая изотопологи)". Структура воды и наука . Лондонский университет Саут-Бэнк. Архивировано из оригинала 21.11.2020.Единственными металлами с энтальпией плавления, не находящейся в диапазоне 6–30 Дж моль ⁻¹  К ^−1, являются (с высокой стороны): Ta, W и Re; и (с низкой стороны) большинство металлов группы 1 (щелочных), а также Ga, In, Hg, Tl, Pb и Np.
35. Для ксенона доступные значения находятся в диапазоне от 2,3 до 3,1 кДж/моль. "Ксенон – 54Xe: основы". WebElements . Получено 24 сентября 2024 г. .Теплота плавления гелия составляет всего 0,021 кДж/моль, что делает силу связи настолько слабой, что нулевая энергия не позволяет гелию замерзнуть, если только он не находится под давлением не менее 25 атмосфер.
36. Справочник CRC по химии и физике , 1-е студенческое издание ^{[ необходима полная ссылка ]}
37. Удельная теплоемкость H _{2 O,} C _p  =0,075 327  кДж⋅моль ⁻¹ ⋅К ⁻¹ (25 °C); энтальпия плавления = 6,0095 кДж/моль (0 °C, 101,325 кПа); энтальпия испарения (жидкость) = 40,657 кДж/моль (100 °C). Чаплин, Мартин. "Свойства воды (включая изотопологи)". Структура воды и наука . Лондонский университет Южного берега. Архивировано из оригинала 21.11.2020.
38. Подвижные электроны проводимости делокализованы , т.е. не привязаны к определенному атому, и ведут себя скорее как своего рода квантовый газ из-за эффектов нулевой энергии. Следовательно, даже при абсолютном нуле электроны проводимости все еще движутся между атомами со скоростью Ферми около1,6 × 10 ⁶  м/с . Кинетическая тепловая энергия увеличивает эту скорость и также заставляет делокализованные электроны перемещаться дальше от ядер.
39. Ни одна другая кристаллическая структура не может превышать плотность упаковки 74,048% плотнейшей упаковки . Две регулярные кристаллические решетки, встречающиеся в природе, которые имеют такую ​​плотность, — это гексагональная плотноупакованная (ГПУ) и гранецентрированная кубическая (ГЦК). Эти регулярные решетки находятся в самом низком возможном энергетическом состоянии. Алмаз — это плотноупакованная структура с кристаллической решеткой ГЦК. Обратите также внимание, что подходящие кристаллические химические соединения , хотя обычно состоят из атомов разных размеров, могут рассматриваться как плотноупакованные структуры при рассмотрении на молекулярном уровне. Одним из таких соединений является распространенный минерал, известный как магниево-алюминиевая шпинель (MgAl ₂ O ₄ ). Он имеет гранецентрированную кубическую кристаллическую решетку, и никакое изменение давления не может привести к образованию решетки с более низким энергетическим состоянием.
40. Почти половина из 92 встречающихся в природе химических элементов, которые могут замерзать в вакууме, также имеют плотно упакованную кристаллическую решетку. Этот набор включает бериллий , осмий , неон и иридий (но исключает гелий), и поэтому имеют нулевую скрытую теплоту фазовых переходов, чтобы вносить вклад во внутреннюю энергию (символ: U ). При расчете энтальпии (формула: {{{1}}} ) внутренняя энергия может исключать различные источники тепловой энергии (в частности, ZPE) в зависимости от характера анализа. Соответственно, все  плотно упакованные вещества T = 0 в идеальном вакууме имеют либо минимальную, либо нулевую энтальпию в зависимости от характера анализа. Alberty, Robert A. (2001). "Использование преобразований Лежандра в химической термодинамике" (PDF) . Чистая и прикладная химия . 73 (8): 1349. doi :10.1351/pac200173081349.
41. Что касается написания "gage" против "gauge" в контексте давлений, измеряемых относительно атмосферного давления, предпочтительное написание варьируется в зависимости от страны и даже от отрасли. Кроме того, оба написания часто используются в пределах определенной отрасли или страны. Отрасли в странах, говорящих на британском английском, обычно используют написание "gauge pressure", чтобы отличить его от прибора для измерения давления, который в Великобритании пишется как pressure gage . По той же причине многие из крупнейших американских производителей датчиков давления и приборов используют написание gage pressure (используемое здесь соглашение) в своей официальной документации, чтобы отличить его от прибора, который пишется как pressure gauge .
42. Давление также должно быть в абсолютных величинах. Воздух, все еще находящийся в шине при избыточном давлении 0 кПа, также расширяется по мере нагревания. Инженеры нередко упускают из виду, что при компенсации температуры нужно работать с точки зрения абсолютного давления. Например, ведущий производитель авиационных шин опубликовал документ о температурной компенсации давления в шинах, в котором в формуле использовалось избыточное давление. Однако высокие задействованные избыточные давления (180 фунтов на кв. дюйм; 12,4 бар; 1,24 МПа) означают, что ошибка будет довольно небольшой. В случае автомобильных шин низкого давления, где избыточное давление обычно составляет около 2 бар (200 кПа), отсутствие регулировки абсолютного давления приводит к значительной ошибке. "Рейтинги авиационных шин" (PDF) . Air Michelin. Архивировано из оригинала (PDF) 2010-02-15.^{[ нужен лучший источник ]}
43. Здесь используется разница в 100 кПа вместо значения 101,325 кПа одной стандартной атмосферы . В 1982 году Международный союз теоретической и прикладной химии (ИЮПАК) рекомендовал, чтобы для целей спецификации физических свойств веществ стандартное давление (атмосферное давление) определялось как точно 100 кПа (≈ 750,062 торр). Помимо того, что это круглое число, это имело очень практический эффект: относительно немногие люди живут и работают точно на уровне моря; 100 кПа соответствует среднему давлению на высоте около 112 метров, что ближе к 194-метровой, мировой медианной высоте обитания человека. Для особо низких давлений или высокоточных работ необходимо измерять истинное атмосферное давление. "Стандартное давление". Compendium of Chemical Terminology (online 3rd ed.). Международный союз теоретической и прикладной химии. 2014. doi : 10.1351/goldbook.S05921.
44. Planck, M. (1945). Трактат по термодинамике . Dover Publications. §§90, 137, уравнения (39), (40) и (65).
45. Здесь нужно добавить причину требования, чтобы функция g ( T ) была монотонной функцией. Эффективность Карно (эффективность всех обратимых двигателей) может быть причиной.
46. Ферми, Э. (1956). Термодинамика . Dover Publications. стр. 48. eq.(64)
47. "Краткая история измерения температуры". Поставщики химикатов . 2024-03-01 . Получено 2024-09-25 .
48. "Термометр Линнея". Архивировано из оригинала 2012-10-30.
49. "Принятие "градуса Цельсия"". Архивировано из оригинала 2016-10-14.
50. Ламберт, Иоганн Генрих (1779). Пирометрия. Берлин: Хауде и Шпенер.
51. Томсон, Уильям (октябрь 1848 г.). «Об абсолютной термометрической шкале». Philosophical Magazine .Также опубликовано в Томсон, Уильям (1882). Математические и физические статьи . Том 1. Издательство Кембриджского университета. С. 100–106.
52. Лемонс, Дон С. (2020). «Глава 4: Абсолютная температура». Термодинамические странности: от Фаренгейта до Клаузиуса (Первое издание MIT Press Paperback). ISBN 978-0-262-53894-7. OCLC  1143850952.
53. Лемонс, Дон С. (2020). «Глава 8: Абсолютная температура — снова». Термодинамические странности: от Фаренгейта до Клаузиуса (1-е издание в мягкой обложке). Кембридж, Массачусетс: MIT Press. ISBN 978-0-262-53894-7. OCLC  1143850952.
54. «Добро пожаловать».
55. "BIPM - 1948". www.bipm.org . Архивировано из оригинала 2015-02-13.
56. «Температурные шкалы с первых дней термометрии до 21 века» (PDF) . www.imeko.org .
57. Куинн, Терри (1990). Температура (2-е изд.). Academic Press. ISBN 0125696817.
58. Согласно Оксфордскому словарю английского языка (OED), термин «термометр Цельсия» использовался по крайней мере еще в 1797 году. Кроме того, термин «термометр Цельсия или Стоградусный термометр» снова использовался в отношении определенного типа термометра по крайней мере еще в 1850 году. OED также цитирует это сообщение о температуре 1928 года: «Моя высота была около 5800 метров, температура была 28° Цельсия». Однако словари стремятся найти самое раннее использование слова или термина и не являются полезным ресурсом в отношении терминологии, используемой на протяжении всей истории науки. Согласно нескольким работам Терри Куинна CBE FRS, директора BIPM (1988–2004), включая Температурные шкалы с первых дней термометрии до 21-го века ^[56] , а также Температура ^[57] , термин Цельсий в связи со шкалой Цельсия вообще не использовался научными или термометрическими сообществами до тех пор, пока CIPM и CGPM не приняли этот термин в 1948 году. BIPM даже не знало, что градус Цельсия использовался спорадически, не в научных целях до этого времени. Двенадцатитомное издание OED 1933 года даже не имело списка для слова Цельсий (но имело списки как для стоградусной , так и для сотенной шкалы в контексте измерения температуры). Принятие Цельсия в 1948 году достигло трех целей:
    1. Все распространённые температурные шкалы имели бы свои единицы, названные в честь кого-то, тесно с ними связанного; а именно: Кельвин, Цельсий, Фаренгейт, Реомюр и Ренкин.
    2. Несмотря на важный вклад Линнея, который придал шкале Цельсия ее современную форму, имя Цельсия было очевидным выбором, поскольку оно начиналось с буквы С. Таким образом, символ °C, который на протяжении столетий использовался в сочетании с названием « стоградус», мог продолжать использоваться и одновременно унаследовал бы интуитивную ассоциацию с новым названием.
    3. Новое название устранило двусмысленность термина «стоградус» , позволив ему ссылаться исключительно на французское название единицы измерения угла.
59. «Добро пожаловать».
60. «Добро пожаловать».
61. «Добро пожаловать».
62. «Добро пожаловать».

Внешние ссылки

• Zero Point Energy и Zero Point Field. Веб-сайт с подробными объяснениями различных квантовых эффектов. Бернард Хайш из Calphysics Institute.