В геометрии точечная группа — это математическая группа операций симметрии ( изометрий в евклидовом пространстве ), имеющих общую неподвижную точку . Начало координат евклидова пространства традиционно принимается за неподвижную точку, и тогда каждая точечная группа в размерности d является подгруппой ортогональной группы O( d ). Точечные группы используются для описания симметрии геометрических фигур и физических объектов, таких как молекулы .
Каждая точечная группа может быть представлена в виде набора ортогональных матриц M , которые преобразуют точку x в точку y согласно y = Mx . Каждый элемент точечной группы является либо поворотом ( определитель M = 1 ), либо отражением или несобственным поворотом (определитель M = −1 ).
Геометрические симметрии кристаллов описываются пространственными группами , которые допускают трансляции и содержат точечные группы в качестве подгрупп. Дискретные точечные группы в более чем одном измерении входят в бесконечные семейства, но из теоремы о кристаллографическом ограничении и одной из теорем Бибербаха каждое число измерений имеет только конечное число точечных групп, которые симметричны относительно некоторой решетки или сетки с этим числом измерений. Это кристаллографические точечные группы .
Точечные группы можно разделить на хиральные (или чисто вращательные) группы и ахиральные группы. [1] Хиральные группы являются подгруппами специальной ортогональной группы SO( d ): они содержат только ортогональные преобразования, сохраняющие ориентацию, т. е. преобразования определителя +1. Ахиральные группы содержат также преобразования определителя −1. В ахиральной группе преобразования, сохраняющие ориентацию, образуют (хиральную) подгруппу индекса 2.
Конечные группы Коксетера или группы отражений — это те точечные группы, которые генерируются исключительно набором отражательных зеркал, проходящих через одну и ту же точку. Группа Коксетера ранга n имеет n зеркал и представлена диаграммой Коксетера–Дынкина . Нотация Коксетера предлагает скобочную нотацию, эквивалентную диаграмме Коксетера, с символами разметки для групп точек вращательной и другой подсимметрии. Группы отражений обязательно ахиральны (за исключением тривиальной группы, содержащей только единичный элемент).
Существует только две одномерные точечные группы: группа тождества и группа отражения.
Точечные группы в двух измерениях , иногда называемые группами розеток .
Они делятся на два бесконечных семейства:
Применение теоремы о кристаллографических ограничениях ограничивает n значениями 1, 2, 3, 4 и 6 для обоих семейств, что дает 10 групп.
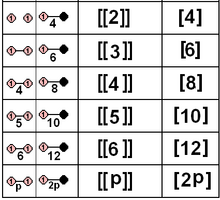
Подмножество чистых отражательных точечных групп, определяемое 1 или 2 зеркалами, также может быть задано их группой Коксетера и связанными с ней многоугольниками. Они включают 5 кристаллографических групп. Симметрия отражательных групп может быть удвоена изоморфизмом , отображающим оба зеркала друг на друга биссекторным зеркалом, удваивая порядок симметрии.
Точечные группы в трех измерениях , иногда называемые молекулярными точечными группами из-за их широкого использования при изучении симметрии молекул .
Они входят в 7 бесконечных семейств аксиальных групп (также называемых призматическими) и 7 дополнительных полиэдральных групп (также называемых платоновыми). В нотации Шёнфлис ,
Применение теоремы о кристаллографическом ограничении к этим группам дает 32 кристаллографические точечные группы .

Группы точек отражения, определяемые 1–3 зеркальными плоскостями, также могут быть заданы их группой Коксетера и связанными с ней многогранниками. Группа [3,3] может быть удвоена, записана как [[3,3]], отображая первое и последнее зеркала друг на друга, удваивая симметрию до 48 и изоморфна группе [4,3].
Четырехмерные точечные группы (как хиральные, так и ахиральные) перечислены в работе Конвея и Смита [1] , раздел 4, таблицы 4.1–4.3.

Следующий список содержит четырехмерные группы отражений (исключая те, которые оставляют подпространство фиксированным и которые, следовательно, являются группами отражений меньшей размерности). Каждая группа определяется как группа Коксетера , и, как и полиэдральные группы 3D, она может быть названа своим связанным выпуклым правильным 4-многогранником . Связанные чистые группы вращения существуют для каждой с половинным порядком и могут быть представлены скобочной нотацией Коксетера с показателем '+', например, [3,3,3] + имеет три 3-кратные точки инерции и порядок симметрии 60. Передне-задние симметричные группы, такие как [3,3,3] и [3,4,3], могут быть удвоены, показаны как двойные скобки в нотации Коксетера, например, [[3,3,3]] с ее порядком, удвоенным до 240.

В следующей таблице приведены пятимерные группы отражения (исключая те, которые являются группами отражения более низкой размерности), перечисленные как группы Коксетера . Для каждой существуют родственные хиральные группы с половинным порядком, и они могут быть представлены скобочной нотацией Коксетера с показателем степени '+', например, [3,3,3,3] + имеет четыре точки 3-кратной инерции и порядок симметрии 360.

В следующей таблице приведены шестимерные группы отражений (исключая те, которые являются группами отражений меньшей размерности), перечисленные как группы Коксетера . Для каждой существуют родственные чистые вращательные группы с половинным порядком, и они могут быть представлены скобочной нотацией Коксетера с показателем степени '+', например, [3,3,3,3,3] + имеет пять 3-кратных точек инерции и порядок симметрии 2520.
В следующей таблице приведены семимерные группы отражений (исключая те, которые являются группами отражений меньшей размерности), перечисленные как группы Коксетера . Связанные хиральные группы существуют для каждой с половинным порядком, определяемым четным числом отражений, и могут быть представлены скобочной нотацией Коксетера с показателем степени '+', например, [3,3,3,3,3,3] + имеет шесть 3-кратных точек инерции и порядок симметрии 20160.
В следующей таблице приведены восьмимерные группы отражений (исключая те, которые являются группами отражений меньшей размерности), перечисленные как группы Коксетера . Связанные хиральные группы существуют для каждой с половинным порядком, определяемым четным числом отражений, и могут быть представлены скобочной нотацией Коксетера с показателем степени '+', например, [3,3,3,3,3,3,3] + имеет семь 3-кратных точек инерции и порядок симметрии 181440.