Пять точек определяют конику

Принцип в геометрии

В евклидовой и проективной геометрии пять точек определяют конику (плоскую кривую степени 2), точно так же, как две (отдельные) точки определяют линию ( плоскую кривую степени 1 ). Для коник существуют дополнительные тонкости , которых нет для прямых, и поэтому утверждение и его доказательство для коник являются более техническими, чем для прямых.

Формально, если любые пять точек плоскости находятся в общем линейном положении , то есть нет трех коллинеарных , то через них проходит единственная коника, которая будет невырожденной ; это верно как для евклидовой плоскости , так и для любой папповской проективной плоскости . Действительно, через любые пять точек проходит коника, но если три точки лежат на одной прямой, коника будет вырожденной (приводимой, поскольку содержит прямую) и может быть не единственной; смотрите дальнейшее обсуждение .

Доказательства

Этот результат можно доказать множеством разных способов; Аргумент подсчета размерностей является наиболее прямым и обобщает в более высокой степени, в то время как другие доказательства относятся только к коникам.

Подсчет размеров

Интуитивно понятно, что прохождение через пять точек в общем линейном положении задает пять независимых линейных ограничений на (проективное) линейное пространство коник и, следовательно, задает уникальную конику, хотя это краткое утверждение игнорирует тонкости.

Точнее, это выглядит следующим образом:

• коники соответствуют точкам в пятимерном проективном пространстве. ${\displaystyle \mathbf {P} ^{5};}$
• Требование, чтобы коника проходила через точку, накладывает линейное условие на координаты: при фиксированном уравнении уравнение является линейным уравнением в ${\displaystyle (x,y),}$ ${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0}$ ${\displaystyle (A,B,C,D,E,F);}$
• при подсчете измерений для определения коники необходимы пять ограничений (что кривая проходит через пять точек), поскольку каждое ограничение сокращает размерность возможностей на 1, а одно начинается с 5 измерений;
• в 5 измерениях пересечение 5 (независимых) гиперплоскостей представляет собой одну точку (формально, по теореме Безу );
• общее линейное положение точек означает, что ограничения независимы и, таким образом, задают уникальную конику;
• результирующая коника невырождена, поскольку она представляет собой кривую (поскольку она имеет более 1 точки) и не содержит линий (в противном случае она разделилась бы на две линии, по крайней мере одна из которых должна содержать 3 из 5 точек, по принципу «ячейки» ), поэтому оно неприводимо.

Две тонкости приведенного выше анализа заключаются в том, что результирующая точка представляет собой квадратное уравнение (а не линейное уравнение) и что ограничения независимы. Первый простой: если A , B и C исчезают, то уравнение определяет линию, и любые 3 точки на ней (фактически любое количество точек) лежат на линии – таким образом, общее линейное положение обеспечивает конику. Второе, что ограничения независимы, значительно тоньше: оно соответствует тому факту, что при наличии пяти точек в общем линейном положении на плоскости их изображения под картой Веронезе находятся в общем линейном положении, что верно, поскольку отображение Веронезе является бирегулярным : т. е. если изображение пяти точек удовлетворяет отношению, то это отношение можно вернуть назад, и исходные точки также должны удовлетворять отношению. Карта Веронезе имеет координаты , а цель двойственна коникам . Отображение Веронезе соответствует «вычислению коники в точке», и утверждение о независимости ограничений является в точности геометрическим утверждением об этом отображении. ${\displaystyle Dx+Ey+F=0}$ ${\displaystyle \mathbf {P} ^{5}}$ ${\displaystyle [x^{2}:xy:y^{2}:xz:yz:z^{2}],}$ ${\displaystyle \mathbf {P} ^{5}}$ ${\displaystyle [A:B:C:D:E:F]}$ ${\displaystyle \mathbf {P} ^{5}}$

Синтетическое доказательство

То, что пять точек определяют конику, может быть доказано синтетической геометрией , т. е. в терминах прямых и точек на плоскости, в дополнение к приведенному выше аналитическому (алгебраическому) доказательству. Такое доказательство можно дать, используя теорему Якоба Штайнера ^[1] , которая гласит:

При проективном преобразовании f между пучком прямых, проходящих через точку X , и пучком прямых, проходящих через точку Y, множество C точек пересечения прямой x и ее изображения образует конику. ${\displaystyle f(x)}$

Обратите внимание, что X и Y находятся на этой конике, если принять во внимание прообраз и образ прямой XY (которая соответственно является линией, проходящей через X , и линией, проходящей через Y ).

Это можно показать, приведя точки X и Y к стандартным точкам и проведя проективное преобразование, при этом пучки прямых соответствуют горизонтальным и вертикальным прямым на плоскости, а пересечения соответствующих прямых - графику функция, которая (необходимо показать) является гиперболой, следовательно, коникой, следовательно, исходная кривая C является коникой. ${\displaystyle [1:0:0]}$ ${\displaystyle [0:1:0]}$

Теперь, учитывая пять точек X, Y, A, B, C, три линии можно преобразовать в три линии с помощью уникального проективного преобразования, поскольку проективные преобразования просто 3-транзитивны на прямых (они просто 3-транзитивны на точках, следовательно, в силу проективной двойственности они 3-транзитивны на прямых). При этом отображении X отображается в Y, поскольку это единственные точки пересечения этих прямых и, таким образом, удовлетворяют условиям теоремы Штейнера. Таким образом, полученная коника содержит все пять точек и, как и хотелось, является единственной такой коникой. ${\displaystyle XA,XB,XC}$ ${\displaystyle YA,YB,YC}$

Построение параболы по пяти точкам

Строительство

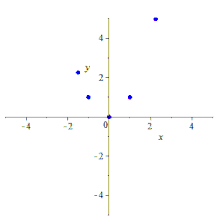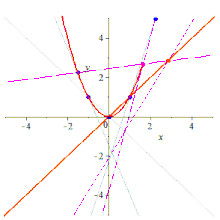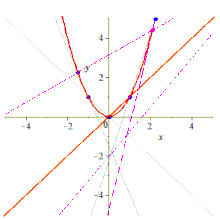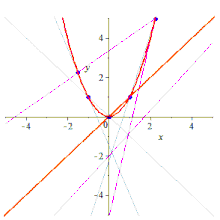
По пяти точкам можно различными способами построить содержащую их конику.

Аналитически, зная координаты пяти точек, уравнение для коники можно найти методом линейной алгебры , написав и решив пять уравнений в коэффициентах, подставив переменные значениями координат: пять уравнений, шесть неизвестных, но однородный, поэтому масштабирование удаляет одно измерение; конкретно, это достигается установкой одного из коэффициентов на 1. ${\displaystyle (x_{i},y_{i})_{i=1,2,3,4,5}}$

Этого можно добиться совершенно напрямую с помощью следующего детерминантного уравнения:

${\displaystyle \det {\begin{bmatrix}x^{2}&xy&y^{2}&x&y&1\\x_{1}^{2}&x_{1}y_{1}&y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}&x_{2}y_{2}&y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}&x_{3}y_{3}&y_{3}^{2}&x_{3}&y_{3}&1\\x_{4}^{2}&x_{4}y_{4}&y_{4}^{2}&x_{4}&y_{4}&1\\x_{5}^{2}&x_{5}y_{5}&y_{5}^{2}&x_{5}&y_{5}&1\end{bmatrix}}=0}$

Эта матрица имеет переменные в первой строке и числа во всех остальных строках, поэтому определитель явно представляет собой линейную комбинацию шести мономов степени не выше 2. Кроме того, полученный полином явно обращается в нуль в пяти входных точках (когда ), как тогда матрица имеет повторяющуюся строку. ${\displaystyle (x,y)=(x_{i},y_{i})}$

Синтетически конику можно построить с помощьюКонструкция Брейкенриджа–Маклорена ,^[2][3][4][5]путем применениятеоремы Брайкенриджа–Маклорена, которая является обратнойтеореме Паскаля. Теорема Паскаля утверждает, что при наличии6точек на конике (шестиугольнике) линии, определяемые противоположными сторонами, пересекаются в трех коллинеарных точках. Это можно изменить, чтобы построить возможные местоположения для 6-й точки, учитывая 5 существующих.

Обобщения

Естественным обобщением является вопрос о том, какое значение k конфигурация k точек (в общем положении) в n -пространстве определяет многообразие степени d и размерности m , что является фундаментальным вопросом в перечислительной геометрии .

Простым случаем этого является гиперповерхность ( подмногообразие коразмерности 1, нули одного многочлена, случай ), примером которой являются плоские кривые. ${\displaystyle m=n-1}$

В случае гиперповерхности ответ дается в терминах коэффициента мультимножества , более привычного биномиального коэффициента или, более элегантно, возрастающего факториала , как:

${\displaystyle k=\left(\!\!{n+1 \choose d}\!\!\right)-1={n+d \choose d}-1={\frac {1}{n!}}(d+1)^{(n)}-1.}$

Это происходит посредством аналогичного анализа отображения Веронезе : k точек в общем положении налагают k независимых линейных условий на многообразие (поскольку отображение Веронезе бирегулярно), а количество мономов степени d от переменных ( n -мерное проективное пространство имеет однородные координаты) — из которого в результате проективизации вычитается 1: умножение многочлена на константу не меняет его нули. ${\displaystyle n+1}$ ${\displaystyle n+1}$ ${\displaystyle \textstyle {\left(\!\!{n+1 \choose d}\!\!\right)},}$

В приведенной выше формуле количество точек k представляет собой полином от d степени n со старшим коэффициентом ${\displaystyle 1/n!}$

В случае плоских кривых формула принимает вид: ${\displaystyle n=2,}$

${\displaystyle \textstyle {\frac {1}{2}}(d+1)(d+2)-1=\textstyle {\frac {1}{2}}(d^{2}+3d)}$

чьи значения для являются - нет кривых степени 0 (одна точка является точкой и, таким образом, определяется точкой, которая имеет коразмерность 2), 2 точки определяют линию, 5 точек определяют конику, 9 точек определяют кубику , 14 точек определяют квартику и т.д. ${\displaystyle d=0,1,2,3,4}$ ${\displaystyle 0,2,5,9,14}$

Связанные результаты

Хотя пять точек определяют конику, наборы из шести или более точек на конике не находятся в общем положении, то есть они ограничены, как показано в теореме Паскаля .

Аналогично, хотя девять точек определяют кубик, но если девять точек лежат более чем на одном кубике (т. е. они являются пересечением двух кубиков), то они не находятся в общем положении и действительно удовлетворяют ограничению сложения, как указано в законе Кэли . – Теорема Бахараха .

Четыре точки определяют не конику, а скорее карандаш , одномерную линейную систему коник , которые все проходят через четыре точки (формально, имеют четыре точки в качестве базового локуса ). Аналогично, три точки определяют 2-мерную линейную систему (сеть), две точки определяют 3-мерную линейную систему (ткань), одна точка определяет 4-мерную линейную систему, а нулевые точки не накладывают ограничений на 5-мерную линейную систему. система всех коник.

Аполлоновы круги — это два однопараметрических семейства, определяемые двумя точками.

Как хорошо известно, три неколлинеарные точки определяют круг в евклидовой геометрии, а две различные точки определяют пучок окружностей , таких как аполлоновы круги . Эти результаты, кажется, противоречат общему результату, поскольку круги являются частным случаем коник. Однако в папповской проективной плоскости коника является окружностью, только если она проходит через две конкретные точки на бесконечной прямой , поэтому окружность определяется пятью неколлинеарными точками, тремя в аффинной плоскости и этими двумя особыми точками. Подобные соображения объясняют меньшее, чем ожидалось, количество точек, необходимых для определения пучков окружностей.

касание

Вместо прохождения через точки другое условие на кривой - касание к данной линии. Касательность к пяти заданным прямым также определяет конику в силу проективной двойственности , но с алгебраической точки зрения касание к прямой является квадратичным ограничением, поэтому наивный подсчет размерностей дает 2 ⁵  = 32 коники, касающихся пяти заданных прямых, из которых 31 должно быть приписано вырожденным коникам, как описано в вымышленных факторах в перечислительной геометрии ; формализация этой интуиции требует значительного дальнейшего развития для обоснования.

Другая классическая задача перечислительной геометрии, аналогичная конической задаче, — это задача Аполлония : окружность, касающаяся трех окружностей, вообще определяет восемь окружностей, поскольку каждая из них представляет собой квадратичное условие и 2 ³  = 8. В качестве вопроса в реальной геометрии полный анализ включает в себя множество особых случаев, и фактическое количество кругов может быть любым числом от 0 до 8, кроме 7.

Смотрите также

• Теорема Крамера (алгебраические кривые) для обобщения на плоские кривые n -й степени.

Рекомендации

1. Интерактивный курс по проективной геометрии. Архивировано 27 ноября 2017 г. в Wayback Machine . Глава пятая: Проективная геометрия коник. Архивировано 22 декабря 2017 г. в Wayback Machine : Раздел четвертый: Коники на реальной проективной плоскости. Архивировано 4 апреля 2018 г. «24 часа в Wayback Machine» , автор: Х. К. Альварес Пайва; доказательство следует из упражнения 4.6.
2. (Коксетер 1961, стр. 252–254)
3. Анимированный Паскаль, Сандра Лах Арлингхаус
4. Вайсштейн, Эрик В. «Строительство Брайкенридж-Маклорена». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Braikenridge-MaclaurinConstruction.html
5. Страница конических сечений GNU 3DLDF: теорема Паскаля и конструкция Брайкенриджа-Маклорена, Лоуренс Д. Финстон

• Коксетер, HSM (1961), Введение в геометрию , Вашингтон, округ Колумбия.{{citation}}: CS1 maint: location missing publisher (link)
• Коксетер, HSM ; Грейцер, С.Л. (1967), «Возвращение к геометрии» , Вашингтон, округ Колумбия: Математическая ассоциация Америки , стр. 76
• Диксон, AC (март 1908 г.), «Коника через пять заданных точек», The Mathematical Gazette , 4 (70), The Mathematical Association: 228–230, doi : 10.2307/3605147, JSTOR  3605147, S2CID  125356690

Внешние ссылки

• Пять точек определяют коническое сечение, интерактивная демонстрация Wolfram