Сопротивление качению

Сила сопротивления движению при качении тела по поверхности

Рисунок 1. Твердое колесо катится по мягкой поверхности и деформируется, в результате чего сила реакции R со стороны поверхности имеет компонент, противодействующий движению. ( W — некоторая вертикальная нагрузка на ось, F — некоторая сила тяги, приложенная к оси, r — радиус колеса, а трение о землю и трение на оси считаются пренебрежимо малыми и поэтому не показаны. Колесо катится влево с постоянной скоростью.) Обратите внимание, что R — результирующая сила от неравномерного давления на поверхности контакта колеса с дорожным полотном. Это давление больше по направлению к передней части колеса из-за гистерезиса.

Сопротивление качению , иногда называемое трением качения или сопротивлением качения , — это сила, сопротивляющаяся движению , когда тело (такое как мяч , шина или колесо ) катится по поверхности. Она в основном вызвана неупругими эффектами; то есть не вся энергия, необходимая для деформации (или движения) колеса, дорожного полотна и т. д., восстанавливается при снятии давления. Двумя формами этого являются потери на гистерезис (см. ниже) и постоянная (пластическая) деформация объекта или поверхности (например, почвы). Обратите внимание, что проскальзывание между колесом и поверхностью также приводит к рассеиванию энергии. Хотя некоторые исследователи включили этот термин в сопротивление качению, некоторые предполагают, что этот термин рассеивания следует рассматривать отдельно от сопротивления качению, поскольку он обусловлен приложенным к колесу крутящим моментом и результирующим проскальзыванием между колесом и землей, что называется потерей скольжения или сопротивлением скольжению. ^[1] Кроме того, только так называемое сопротивление скольжению включает трение , поэтому название «трение качения» в некоторой степени неверно.

Аналогично трению скольжения , сопротивление качению часто выражается как коэффициент, умноженный на нормальную силу. Этот коэффициент сопротивления качению обычно намного меньше коэффициента трения скольжения. ^[2]

Любое движущееся по инерции колесное транспортное средство будет постепенно замедляться из-за сопротивления качению, включая сопротивление подшипников, но вагон поезда со стальными колесами, движущийся по стальным рельсам, будет катиться дальше, чем автобус той же массы с резиновыми шинами, движущийся по асфальту/бетону . Факторами, которые способствуют сопротивлению качению, являются (величина) деформации колес, деформация поверхности дорожного полотна и движение под поверхностью. Дополнительные способствующие факторы включают диаметр колеса, ^[3] нагрузку на колесо, поверхностное сцепление, скольжение и относительное микроскольжение между поверхностями контакта. Потери из-за гистерезиса также сильно зависят от свойств материала колеса или шины и поверхности. Например, резиновая шина будет иметь более высокое сопротивление качению на асфальтированной дороге, чем стальное железнодорожное колесо на стальном рельсе. Кроме того, песок на земле даст большее сопротивление качению, чем бетон . Единственный фактор сопротивления качению не зависит от скорости.

Основная причина

Асимметричное распределение давления между катящимися цилиндрами из-за вязкоупругого поведения материала (катящийся вправо). ^[4]

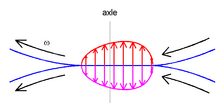
Основной причиной сопротивления качению пневматических шин является гистерезис : ^[5]

Характеристика деформируемого материала, при которой энергия деформации больше энергии восстановления. Резиновая смесь в шине проявляет гистерезис. Когда шина вращается под весом транспортного средства, она испытывает повторяющиеся циклы деформации и восстановления и рассеивает потерю энергии гистерезиса в виде тепла. Гистерезис является основной причиной потери энергии, связанной с сопротивлением качению, и объясняется вязкоупругими характеристиками резины.

— Национальная академия наук ^[6]

Этот основной принцип проиллюстрирован на рисунке катящихся цилиндров. Если два одинаковых цилиндра прижаты друг к другу, то контактная поверхность будет плоской. При отсутствии поверхностного трения контактные напряжения нормальны (т. е. перпендикулярны) к контактной поверхности. Рассмотрим частицу, которая входит в область контакта с правой стороны, проходит через пятно контакта и выходит с левой стороны. Первоначально ее вертикальная деформация увеличивается, чему препятствует эффект гистерезиса. Поэтому создается дополнительное давление, чтобы избежать взаимопроникновения двух поверхностей. Позже ее вертикальная деформация уменьшается. Этому снова препятствует эффект гистерезиса. В этом случае это уменьшает давление, необходимое для удержания двух тел отдельно.

Результирующее распределение давления асимметрично и смещено вправо. Линия действия (совокупной) вертикальной силы больше не проходит через центры цилиндров. Это означает, что возникает момент , который стремится замедлить движение качения.

Материалы, которые имеют большой эффект гистерезиса, такие как резина, которые медленно отскакивают, демонстрируют большее сопротивление качению, чем материалы с небольшим эффектом гистерезиса, которые отскакивают быстрее и полнее, такие как сталь или кремний . Шины с низким сопротивлением качению обычно включают кремний вместо сажи в состав протектора, чтобы уменьшить низкочастотный гистерезис без ущерба для тяги. ^[7] Обратите внимание, что железные дороги также имеют гистерезис в структуре дорожного полотна. ^[8]

Определения

В широком смысле, удельное «сопротивление качению» (для транспортных средств) — это сила на единицу веса транспортного средства, необходимая для движения транспортного средства по ровной поверхности с постоянной низкой скоростью, где аэродинамическое сопротивление (сопротивление воздуха) незначительно, а также где нет тяговых (моторных) сил или тормозов. Другими словами, транспортное средство двигалось бы по инерции, если бы не сила, поддерживающая постоянную скорость. ^[9] Этот широкий смысл включает сопротивление подшипника колеса, энергию, рассеиваемую вибрацией и колебанием как дорожного полотна, так и транспортного средства, и скольжение колеса по поверхности дорожного полотна (тротуару или рельсу).

Но есть еще более широкий смысл, который включает энергию, потраченную впустую из-за проскальзывания колес из-за крутящего момента, приложенного от двигателя. Это включает в себя повышенную мощность, требуемую из-за возросшей скорости колес, где тангенциальная скорость ведущего колеса(колес) становится больше скорости транспортного средства из-за проскальзывания. Поскольку мощность равна силе, умноженной на скорость , и скорость колеса увеличилась, требуемая мощность соответственно увеличилась.

Чистое «сопротивление качению» для поезда — это то, что происходит из-за деформации и возможного незначительного скольжения в контакте колеса с дорогой. ^[10] Для резиновой шины аналогичная потеря энергии происходит по всей шине, но она все равно называется «сопротивлением качению». В широком смысле «сопротивление качению» включает сопротивление подшипника колеса, потерю энергии при сотрясении как дорожного полотна (и земли под ним), так и самого транспортного средства, а также при скольжении колеса, контакте дороги с рельсами. Железнодорожные учебники, кажется, охватывают все эти силы сопротивления, но не называют их сумму «сопротивлением качению» (в широком смысле), как это сделано в этой статье. Они просто суммируют все силы сопротивления (включая аэродинамическое сопротивление) и называют сумму базовым сопротивлением поезда (или тому подобным). ^[11]

Поскольку сопротивление качению на железной дороге в широком смысле может быть в несколько раз больше, чем просто чистое сопротивление качению ^[12], сообщаемые значения могут находиться в серьезном противоречии, поскольку они могут основываться на разных определениях «сопротивления качению». Двигатели поезда, конечно, должны обеспечивать энергию для преодоления этого сопротивления качению в широком смысле.

Для шин сопротивление качению определяется как энергия, потребляемая шиной на единицу пройденного расстояния. Его также называют трением качения или сопротивлением качения. Это одна из сил, которая действует, чтобы противостоять движению водителя. Основная причина этого заключается в том, что когда шины находятся в движении и касаются поверхности, поверхность меняет форму и вызывает деформацию шины. ^[13]

Для дорожных транспортных средств часть энергии рассеивается при сотрясении дорожного полотна (и земли под ним), сотрясении самого транспортного средства и скольжении шин. Но, за исключением дополнительной мощности, требуемой из-за крутящего момента и трения подшипников колеса, нечистое сопротивление качению, похоже, не было исследовано, возможно, потому, что «чистое» сопротивление качению резиновой шины в несколько раз выше, чем пренебрегаемые сопротивления. ^[14]

Коэффициент сопротивления качению

«Коэффициент сопротивления качению» определяется следующим уравнением: ^[6] где $${\displaystyle \ F=C_{rr}N}$$

• ${\displaystyle F}$- сила сопротивления качению (показана на рисунке 1), ${\displaystyle R}$
• ${\displaystyle C_{rr}}$— безразмерный коэффициент сопротивления качению или коэффициент трения качения ( CRF ), а
• ${\displaystyle N}$это нормальная сила , сила, перпендикулярная поверхности, по которой катится колесо.

${\displaystyle C_{rr}}$это сила, необходимая для толкания (или буксировки) колесного транспортного средства вперед (с постоянной скоростью на ровной поверхности или нулевом уклоне с нулевым сопротивлением воздуха) на единицу силы веса. Предполагается, что все колеса одинаковы и несут одинаковый вес. Таким образом: означает, что для буксировки транспортного средства весом в один фунт потребуется всего 0,01 фунта. Для транспортного средства весом 1000 фунтов потребуется в 1000 раз больше силы буксировки, т. е. 10 фунтов. Можно сказать, что это в фунтах (сила буксировки)/фунтах (вес транспортного средства). Поскольку этот фунт/фунт представляет собой силу, деленную на силу, является безразмерным. Умножьте его на 100, и вы получите процент (%) веса транспортного средства, необходимый для поддержания медленной постоянной скорости. часто умножается на 1000, чтобы получить части на тысячу, что то же самое, что килограммы (кг силы) на метрическую тонну (тонна = 1000 кг), ^[15] что то же самое, что фунты сопротивления на 1000 фунтов груза или ньютоны/килоньютон и т. д. Для железных дорог США традиционно использовался фунт/тонна; это просто . Таким образом, все они являются просто мерами сопротивления на единицу веса транспортного средства. Хотя все они являются «удельными сопротивлениями», иногда их просто называют «сопротивлением», хотя на самом деле они являются коэффициентом (отношением) или кратным ему. Если использовать фунты или килограммы в качестве единиц силы, масса равна весу (в земной гравитации килограмм массы весит килограмм и оказывает килограмм силы), поэтому можно утверждать, что это также сила на единицу массы в таких единицах. Система СИ будет использовать Н/тонну (Н/Т, Н/т), что равно силе на единицу массы, где g — ускорение свободного падения в единицах СИ (метры на секунду в квадрате). ^[16] ${\displaystyle \ C_{rr}=0.01}$ ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle 2000C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle 1000gC_{rr}}$

Вышеуказанное показывает сопротивление, пропорциональное , но явно не показывает никаких изменений в зависимости от скорости, нагрузки, крутящего момента, шероховатости поверхности, диаметра, накачки/износа шин и т. д., поскольку само изменяется в зависимости от этих факторов. Из приведенного выше определения может показаться, что сопротивление качению прямо пропорционально весу транспортного средства, но это не так. ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$ ${\displaystyle C_{rr}}$

Измерение

Существует как минимум две популярные модели расчета сопротивления качению.

1. «Коэффициент сопротивления качению (RRC). Значение силы сопротивления качению, деленное на нагрузку на колесо. Общество инженеров-автомобилестроителей (SAE) разработало методики испытаний для измерения RRC шин. Эти испытания ( SAE J1269 и SAE J2452 ) обычно проводятся ^{[ требуется ссылка ]} на новых шинах. При измерении с использованием этих стандартных методик испытаний большинство новых легковых шин показали RRC в диапазоне от 0,007 до 0,014». ^[6] В случае велосипедных шин достигаются значения от 0,0025 до 0,005. ^[17] Эти коэффициенты измеряются на роликах, с помощью измерителей мощности на дорожном покрытии или с помощью испытаний накатом. В последних двух случаях необходимо вычесть влияние сопротивления воздуха или провести испытания на очень низких скоростях.
2. Коэффициент сопротивления качению b , имеющий размерность длины , приблизительно (в силу малоуглового приближения ) равен значению силы сопротивления качению, умноженному на радиус колеса, делённому на нагрузку на колесо. ^[3] ${\displaystyle \cos(\theta )=1}$
3. В Европе для испытания сопротивления качению используется стандарт ISO 18164:2005.

Результаты этих испытаний могут быть труднодоступны для широкой публики, поскольку производители предпочитают рекламировать «комфорт» и «производительность».

Физические формулы

Коэффициент сопротивления качению для медленного жесткого колеса на идеально упругой поверхности, не скорректированный по скорости, можно рассчитать по формуле ^{[18] [ необходима ссылка ]} , где $${\displaystyle C_{rr}={\sqrt {z/d}}}$$

• ${\displaystyle z}$это глубина погружения
• ${\displaystyle d}$диаметр жесткого колеса

Эмпирическая формула для чугунных колес шахтных вагонеток на стальных рельсах выглядит следующим образом: ^[19] где ${\displaystyle C_{rr}}$ $${\displaystyle C_{rr}=0.0048(18/D)^{\frac {1}{2}}(100/W)^{\frac {1}{4}}={\frac {0.0643988}{\sqrt[{4}]{WD^{2}}}}}$$

• ${\displaystyle D}$диаметр колеса в дюймах
• ${\displaystyle W}$это нагрузка на колесо в фунтах-силах

В качестве альтернативы использованию C r r {\displaystyle C_{rr}} можно использовать , который является другим коэффициентом сопротивления качению или коэффициентом трения качения с размерностью длины. Он определяется следующей формулой: ^[3] где ${\displaystyle b}$ $${\displaystyle F={\frac {Nb}{r}}}$$

• ${\displaystyle F}$- сила сопротивления качению (показана на рисунке 1),
• ${\displaystyle r}$радиус колеса,
• ${\displaystyle b}$- коэффициент сопротивления качению или коэффициент трения качения с размерностью длины, и
• ${\displaystyle N}$— нормальная сила (равная W , а не R , как показано на рисунке 1).

Приведенное выше уравнение, где сопротивление обратно пропорционально радиусу, по-видимому, основано на дискредитированном «законе Кулона» (ни закон обратных квадратов Кулона, ни закон трения Кулона) ^{[ требуется ссылка ]} . См. зависимость от диаметра. Приравнивая это уравнение к силе, действующей на коэффициент сопротивления качению, и решая для , получаем = . Следовательно, если источник дает коэффициент сопротивления качению ( ) как безразмерный коэффициент, его можно преобразовать в , имеющий единицы длины, умножив на радиус колеса . ${\displaystyle r}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle C_{rr}r}$ ${\displaystyle C_{rr}}$ ${\displaystyle b}$ ${\displaystyle C_{rr}}$ ${\displaystyle r}$

Примеры коэффициента сопротивления качению

Таблица примеров коэффициента сопротивления качению: [3]

Например, в условиях земного притяжения автомобилю массой 1000 кг для качения по асфальту потребуется сила около 100  ньютонов (1000 кг × 9,81 м/с2 ^× 0,01 = 98,1 Н).

Зависимость от диаметра

Дилижансы и железные дороги

Согласно Дюпюи (1837), сопротивление качению (колесных экипажей с деревянными колесами с железными шинами) приблизительно обратно пропорционально квадратному корню из диаметра колеса. ^[34] Это правило было экспериментально проверено для чугунных колес (диаметром 8″ - 24″) на стальном рельсе ^[35] и для колес экипажей 19-го века. ^[33] Но есть и другие испытания колес экипажей, которые не согласуются с этим. ^[33] Теория цилиндра, катящегося по упругой дороге, также дает это же правило ^[36] Они противоречат более ранним (1785) испытаниям Кулона катящихся деревянных цилиндров, в которых Кулон сообщил, что сопротивление качению было обратно пропорционально диаметру колеса (известному как «закон Кулона»). ^[37] Однако этот спорный (или неправильно применяемый) «закон Кулона» все еще встречается в справочниках.

Пневматические шины

Для пневматических шин на твердом покрытии сообщается, что влияние диаметра на сопротивление качению незначительно (в пределах практического диапазона диаметров). ^{[38] [39]}

Зависимость от приложенного крутящего момента

Крутящий момент , необходимый для преодоления сопротивления качению и поддержания постоянной скорости на ровной поверхности (без сопротивления воздуха), можно рассчитать по формуле: где ${\displaystyle T}$ ${\displaystyle R_{r}}$ $${\displaystyle T={\frac {V_{s}}{\Omega }}R_{r}}$$

• ${\displaystyle V_{s}}$- линейная скорость тела (на оси), а
• ${\displaystyle \Omega }$его скорость вращения.

Примечательно, что обычно не равен радиусу тела качения из-за проскальзывания колеса. ^{[40] [41] [42]} Проскальзывание между колесом и землей неизбежно происходит всякий раз, когда к колесу прикладывается крутящий момент или момент торможения. ^{[43] [44]} Следовательно, линейная скорость транспортного средства отличается от окружной скорости колеса. Примечательно, что проскальзывание не происходит в ведущих колесах, которые не подвергаются крутящему моменту, при других условиях, кроме торможения. Поэтому сопротивление качению, а именно потери на гистерезис, является основным источником рассеивания энергии в ведомых колесах или осях, тогда как в ведущих колесах и осях сопротивление скольжению, а именно потери из-за проскальзывания колес, играет такую ​​же роль, как и сопротивление качению. ^[45] Значение сопротивления качению или проскальзыванию во многом зависит от силы тяги , коэффициента трения, нормальной нагрузки и т. д. ^[46] ${\displaystyle V_{s}/\Omega }$

Все колеса

«Приложенный крутящий момент» может быть либо крутящим моментом, приложенным двигателем (часто через трансмиссию ), либо тормозным моментом, приложенным тормозами (включая рекуперативное торможение ). Такие крутящие моменты приводят к рассеиванию энергии (выше, чем из-за основного сопротивления качению свободно катящегося автомобиля, т. е. за исключением сопротивления скольжению). Эта дополнительная потеря отчасти обусловлена ​​тем, что колесо проскальзывает, а для пневматических шин наблюдается больший изгиб боковин из-за крутящего момента. Проскальзывание определяется таким образом, что 2% проскальзывания означает, что окружная скорость ведущего колеса превышает скорость транспортного средства на 2%.

Небольшой процент проскальзывания может привести к сопротивлению проскальзывания, которое намного больше, чем базовое сопротивление качению. Например, для пневматических шин проскальзывание на 5% может привести к увеличению сопротивления качению на 200%. ^[47] Это отчасти потому, что сила тяги, приложенная во время этого проскальзывания, во много раз больше силы сопротивления качению, и, таким образом, прикладывается гораздо больше мощности на единицу скорости (вспомним, мощность = сила x скорость, так что мощность на единицу скорости — это просто сила). Таким образом, даже небольшое процентное увеличение окружной скорости из-за проскальзывания может привести к потере тяговой мощности, которая может даже превысить потерю мощности из-за базового (обычного) сопротивления качению. Для железных дорог этот эффект может быть еще более выраженным из-за низкого сопротивления качению стальных колес.

Показано, что для легкового автомобиля при силе тяги , составляющей около 40% от максимальной силы тяги, сопротивление скольжению практически равно базовому сопротивлению качению (гистерезисные потери). Но при силе тяги, равной 70% от максимальной силы тяги, сопротивление скольжению становится в 10 раз больше базового сопротивления качению. ^[1]

Колеса стальные железнодорожные

Для того чтобы колеса имели хоть какое-то сцепление , требуется некоторое проскальзывание колеса. ^[48] Для поездов, поднимающихся наверх, это проскальзывание обычно составляет от 1,5% до 2,5%.

Проскальзывание (также известное как проскальзывание ) обычно примерно прямо пропорционально тяговому усилию . Исключением является случай, когда тяговое усилие настолько велико, что колесо близко к существенному проскальзыванию (больше, чем несколько процентов, как обсуждалось выше), тогда проскальзывание быстро увеличивается с тяговым усилием и больше не является линейным. При немного большем приложенном тяговом усилии колесо выходит из-под контроля, и сцепление падает , в результате чего колесо вращается еще быстрее. Это тип проскальзывания, который можно наблюдать невооруженным глазом — проскальзывание, скажем, 2% для тяги, наблюдается только приборами. Такое быстрое проскальзывание может привести к чрезмерному износу или повреждению.

Пневматические шины

Сопротивление качению значительно увеличивается с приложенным крутящим моментом. При высоких крутящих моментах, которые прикладывают к дороге тангенциальную силу, составляющую около половины веса транспортного средства, сопротивление качению может утроиться (увеличение на 200%). ^[47] Это частично связано с проскальзыванием около 5%. Увеличение сопротивления качению с приложенным крутящим моментом не линейно, а увеличивается с большей скоростью по мере увеличения крутящего момента.

Зависимость от нагрузки на колесо

Колеса стальные железнодорожные

Коэффициент сопротивления качению, Crr, значительно уменьшается с увеличением веса вагона на колесо. ^[49] Например, пустой грузовой вагон имел Crr примерно в два раза больше, чем загруженный вагон (Crr=0,002 против Crr=0,001). Эта же «экономия масштаба» проявляется при испытании шахтных вагонов. ^[50] Теоретический Crr для жесткого колеса, катящегося по упругому дорожному полотну, показывает Crr обратно пропорциональна квадратному корню нагрузки. ^[36]

Если Crr сам по себе зависит от нагрузки на колесо по правилу обратного квадратного корня, то при увеличении нагрузки на 2% происходит только 1%-ное увеличение сопротивления качению. ^[51]

Пневматические шины

Для пневматических шин направление изменения Crr (коэффициента сопротивления качению) зависит от того, увеличивается ли накачка шин с увеличением нагрузки. ^[52] Сообщается, что если давление в шинах увеличивается с нагрузкой в ​​соответствии с (неопределенным) «графиком», то увеличение нагрузки на 20% уменьшает Crr на 3%. Но если давление в шинах не меняется, то увеличение нагрузки на 20% приводит к увеличению Crr на 4%. Конечно, это увеличит сопротивление качению на 20% из-за увеличения нагрузки плюс 1,2 x 4% из-за увеличения Crr, что приводит к увеличению сопротивления качению на 24,8%. ^[53]

Зависимость от кривизны проезжей части

Общий

Когда транспортное средство ( автомобиль или железнодорожный поезд ) движется по кривой, сопротивление качению обычно увеличивается. Если кривая не наклонена так, чтобы точно противодействовать центробежной силе с равной и противоположной центростремительной силой из-за наклона, то на транспортное средство будет действовать чистая несбалансированная боковая сила. Это приведет к увеличению сопротивления качению. Наклон также известен как «суперэлевация» или «наклон» (не путать с наклоном рельса ) . Для железных дорог это называется сопротивлением качению , но для автомобильных дорог это (по крайней мере однажды) называлось сопротивлением качению из- за поворота .

Звук

Трение качения генерирует звуковую (вибрационную) энергию, поскольку механическая энергия преобразуется в эту форму энергии из-за трения. Одним из наиболее распространенных примеров трения качения является движение шин автомобиля по дороге , процесс, который генерирует звук как побочный продукт. ^[54] Звук, создаваемый автомобильными и грузовыми шинами при их вращении (особенно заметный на скоростях шоссе), в основном обусловлен ударами протекторов шин и сжатием (и последующей декомпрессией) воздуха, временно захваченного внутри протекторов. ^[55]

Факторы, влияющие на шины

На величину сопротивления качению, создаваемого шиной, влияют несколько факторов:

• Как упоминалось во введении: радиус колеса, скорость движения, сцепление с поверхностью и относительное микроскольжение.
• Материал - различные наполнители и полимеры в составе шин могут улучшить сцепление, одновременно уменьшая гистерезис. Замена части технического углерода на более дорогой кремний-силан является одним из распространенных способов снижения сопротивления качению. ^[6] Было показано, что использование экзотических материалов, включая наноглину, снижает сопротивление качению в высокопроизводительных резиновых шинах. ^[56] Растворители также могут использоваться для разбухания цельных шин, уменьшая сопротивление качению. ^[57]
• Размеры - сопротивление качению в шинах связано с гибкостью боковин и площадью контакта шины ^[58] Например, при том же давлении более широкие велосипедные шины меньше изгибаются в боковинах при качении и, таким образом, имеют меньшее сопротивление качению (хотя и большее сопротивление воздуха). ^[58]
• Степень накачки - Более низкое давление в шинах приводит к большему изгибу боковин и более высокому сопротивлению качению. ^[58] Это преобразование энергии в боковинах увеличивает сопротивление и также может привести к перегреву и, возможно, сыграло свою роль в печально известных авариях с опрокидыванием Ford Explorer .
• Перекачивание шин (например, велосипедных) может не снизить общее сопротивление качению, поскольку шина может подпрыгивать и скакать по поверхности дороги. Сцепление ухудшается, а общее трение качения может не уменьшиться, поскольку скорость вращения колеса изменяется, а проскальзывание увеличивается. ^{[ необходима цитата ]}
• Прогиб боковины не является прямым измерением трения качения. Высококачественная шина с высококачественным (и гибким) каркасом обеспечит большую гибкость за единицу потери энергии, чем дешевая шина с жесткой боковиной. ^{[ требуется ссылка ]} Опять же, на велосипеде качественная шина с гибким каркасом все равно будет катиться легче, чем дешевая шина с жестким каркасом. Аналогично, как отметили в Goodyear Truck Tyres, шина с «топливосберегающим» каркасом принесет пользу в плане экономии топлива в течение многих сроков службы протектора (т. е. восстановления), в то время как шина с «топливосберегающим» рисунком протектора принесет пользу только до тех пор, пока протектор не износится.
• В шинах толщина и форма протектора во многом связаны с сопротивлением качению. Чем толще и рельефнее протектор, тем выше сопротивление качению ^[58] Таким образом, «самые быстрые» велосипедные шины имеют очень маленький протектор, а тяжелые грузовики получают лучшую экономию топлива по мере износа протектора.
• Влияние диаметра, по-видимому, незначительно, если дорожное покрытие твердое, а диапазон диаметров ограничен. См. зависимость от диаметра.
• Практически все мировые рекорды скорости были установлены на относительно узких колесах, ^{[ необходима ссылка ]} вероятно, из-за их аэродинамического преимущества на высокой скорости, которое гораздо менее важно на обычных скоростях.
• Температура: как для цельнолитых, так и для пневматических шин было обнаружено, что сопротивление качению уменьшается с ростом температуры (в пределах диапазона температур: т. е. существует верхний предел этого эффекта) ^{[59] [60]} При повышении температуры от 30 °C до 70 °C сопротивление качению уменьшается на 20-25%. ^[61] Гонщики нагревают свои шины перед гонкой, но это в первую очередь используется для увеличения трения шин, а не для уменьшения сопротивления качению.

Железные дороги: компоненты сопротивления качению

В широком смысле сопротивление качению можно определить как сумму компонентов ^[62] ):

1. Потери крутящего момента в подшипниках колес.
2. Чистое сопротивление качению.
3. Скольжение колеса по рельсу.
4. Потеря энергии в дорожном полотне (и земле).
5. Потери энергии на колебания железнодорожного подвижного состава.

Потери крутящего момента подшипника колеса можно измерить как сопротивление качению на ободе колеса, Crr. На железных дорогах обычно используются роликовые подшипники, которые являются либо цилиндрическими (Россия) ^[63] , либо коническими (США). ^[64] Удельное сопротивление качению в подшипниках меняется как в зависимости от нагрузки на колесо, так и от скорости. ^[65] Сопротивление качению подшипника колеса является самым низким при высоких нагрузках на ось и промежуточных скоростях 60–80 км/ч с Crr 0,00013 (нагрузка на ось 21 тонна). Для пустых грузовых вагонов с нагрузкой на ось 5,5 тонн Crr увеличивается до 0,00020 при 60 км/ч, но при низкой скорости 20 км/ч он увеличивается до 0,00024, а при высокой скорости (для грузовых поездов) 120 км/ч он составляет 0,00028. Полученный выше Crr добавляется к Crr других компонентов, чтобы получить общий Crr для колес.

Сравнение сопротивления качению автотранспортных средств и поездов

Сопротивление качению стальных колес поезда по стальному рельсу намного меньше, чем у резиновых шин колес автомобиля или грузовика. Вес поездов сильно различается; в некоторых случаях они могут быть намного тяжелее на пассажира или на чистую тонну груза, чем автомобиль или грузовик, но в других случаях они могут быть намного легче.

В качестве примера очень тяжелого пассажирского поезда, в 1975 году пассажирские поезда Amtrak весили чуть более 7 тонн на пассажира, ^[66] что намного тяжелее, чем в среднем чуть более одной тонны на пассажира для автомобиля. Это означает, что для пассажирского поезда Amtrak в 1975 году большая часть экономии энергии за счет более низкого сопротивления качению была потеряна из-за его большего веса.

Примером очень легкого высокоскоростного пассажирского поезда является N700 Series Shinkansen , который весит 715 тонн и перевозит 1323 пассажира, в результате чего вес на одного пассажира составляет около полутонны. Этот более легкий вес на одного пассажира в сочетании с более низким сопротивлением качению стальных колес на стальном рельсе означает, что N700 Shinkansen гораздо более энергоэффективен, чем типичный автомобиль.

Что касается грузоперевозок, то в 2013 году компания CSX провела рекламную кампанию, в которой утверждалось, что ее грузовые поезда перевозят «тонну груза на 436 миль на одном галлоне топлива», в то время как некоторые источники утверждают, что грузовики перевозят тонну груза на расстояние около 130 миль на одном галлоне топлива, что свидетельствует о большей эффективности поездов в целом.

Смотрите также

• Коэффициент трения
• Шины с низким сопротивлением качению
• Маглев ( магнитная левитация , устранение качения и, следовательно, сопротивления качению)
• Подшипник качения

Ссылки

1. Sina, Naser; Esfahanian, Vahid; Yazdi, Mohammad Reza Hairi; Azadi, Shahram (18 апреля 2018 г.). "SAE MOBILUS". SAE International Journal of Passenger Cars - Mechanical Systems . 11 (2): 167–176. doi :10.4271/06-11-02-0014 . Получено 19 апреля 2021 г.
2. Пек, Уильям Гай (1859). Элементы механики: для использования в колледжах, академиях и средних школах. AS Barnes & Burr: Нью-Йорк. стр. 135. Получено 09.10.2007 . трение качения меньше трения скольжения.
3. Хиббелер, RC (2007). Инженерная механика: статика и динамика (одиннадцатое изд.). Pearson, Prentice Hall. стр. 441–442. ISBN 9780132038096.
4. "Руководство пользователя для КОНТАКТА, Контакт качения и скольжения с трением. Технический отчет TR09-03 версия v16.1. VORtech, 2016" (PDF) . Получено 2017-07-11 .
5. Справочник по сопротивлению качению пневматических шин Кларк, Сэмюэл Келли; Додж, Ричард Н. 1979
6. "Шины и экономия топлива легковыми автомобилями: информирование потребителей, повышение производительности — Специальный отчет 286. Национальная академия наук, Совет по транспортным исследованиям, 2006" (PDF) . Получено 11 августа 2007 г.
7. Tyres-Online: Преимущества использования силики в конструкции шин. Архивировано 04.02.2013 на Wayback Machine.
8. Астахов, стр.85
9. Пример такого использования для железных дорог можно посмотреть здесь.
10. Деев, стр. 79. Хей, стр. 68
11. Астахов, Гл. IV, с. 73+; Деев, Разд. 5,2 стр. 78+; Хэй, глава. 6 «Поезд Сопротивления» с. 67+
12. Астахов, Рис. 4.14, с. 107
13. "Сопротивление качению и экономия топлива" (PDF) . Архивировано из оригинала (PDF) 2016-04-08.
14. Если предположить, что коэффициенты сопротивления (Crr) для автотранспортных средств такие же, как и для поездов, то для поездов пренебрежимые сопротивления, взятые вместе, имеют Crr около 0,0004 (см. Астахов, рис. 4.14, стр. 107 при 20 км/ч и предположим общий Crr = 0,0010 на основе рис. 3.8, стр. 50 (подшипники скольжения) и скорректируем для роликовых подшипников на основе дельта Crr 0,00035, как показано на рис. 4.2 и 4.4 на стр. 74, 76). Сравните этот Crr 0,0004 с Crr шин автотранспортных средств, которые по крайней мере в 10 раз выше, согласно "Примерам коэффициента сопротивления качению" в этой статье
15. кгс/тонна используется Астаховым на протяжении всей его книги
16. Деев использует нотацию N/T. См. стр. 78-84.
17. Уиллетт, Крейг. «Данные о роликах». www.biketechreview.com . Получено 05.08.2017 .
18. Guiggiani, Massimo (5 мая 2018 г.). Наука динамики транспортных средств . Springer Cham. стр. 22. ISBN 978-3-319-73220-6.
19. Херси, уравнение (2), стр. 83
20. Астахов, стр. 81.
21. "Коэффициенты трения в подшипниках". Коэффициенты трения . Получено 7 февраля 2012 г.
22. ETH - PAC-Car II против PAC-Car I - Техника
23. Roche, Schinkel, Storey, Humphris & Guelden, «Скорость света». ISBN 0-7334-1527-X 
24. Хей, Рис. 6-2, стр. 72 (наихудший случай, показанный для 0,0036, не использован, поскольку он, вероятно, ошибочен)
25. Астахов, Рис. 3.8, 3.9, 3.11, стр. 50-55; Рис. 2.3, 2.4 стр. 35-36. (Худший случай — 0,0024 для нагрузки на ось 5,95 тонн с устаревшими подшипниками скольжения (качения, а не качения)
26. Астахов, рис. 2.1, стр.22
27. Херси, Таблица 6, стр.267
28. «Данные роликов» (PDF) .
29. Crr для больших грузовых шин по Michelin
30. Приложение 1, Часть A. Шины категории C1 (легковые автомобили) Регламента (ЕС) 2020/740 Европейского парламента и Совета от 25 мая 2020 года о маркировке шин в отношении топливной экономичности и других параметров.
31. Отчет Green Seal 2003
32. Gillespie ISBN 1-56091-199-9 стр. 117 
33. Baker, Ira O., "Treatise on roads and pavements". Нью-Йорк, John Wiley, 1914. Stagecoach: Таблица 7, стр. 28. Диаметр: стр. 22-23. В этой книге приводятся несколько сотен значений сопротивления качению для различных транспортных средств, приводимых в движение животными, при различных условиях, в основном по данным 19 века.
34. Херси, подраздел: «Конец темных веков», стр.261
35. Херси, подраздел: «Статическое трение качения», стр.266.
36. Williams, 1994, гл. "Rolling contacts", ур. 11.1, стр. 409.
37. Херси, подраздел: «Кулон на деревянных цилиндрах», стр. 260
38. Национальное бюро стандартов США, рис. 1.13
39. Некоторые ^{[ кто? ]} считают, что колеса с шинами меньшего размера, при прочих равных условиях, как правило, имеют более высокое сопротивление качению, чем колеса большего размера. Однако в некоторых лабораторных испытаниях, таких как результаты испытаний Greenspeed (дата доступа = 2007-10-27), колеса меньшего размера, по-видимому, имели такие же или меньшие потери, чем колеса большего размера, но эти испытания проводились с вращением колес по барабану малого диаметра, что теоретически устранило бы преимущество колес большого диаметра, таким образом делая испытания нерелевантными для решения этой проблемы. Другой контрпример к утверждению о том, что колеса меньшего размера имеют более высокое сопротивление качению, можно найти в области гонок на предельной скорости Soap Box Derby. В этой гонке скорости увеличились, поскольку диаметры колес уменьшились до 50%. Это может означать, что сопротивление качению может не увеличиваться значительно с меньшим диаметром в практическом диапазоне, если бы контролировались любые другие из многих задействованных переменных. См. страницу обсуждения .
40. Зеиль, Жерар-Филипп; Гэвин, Анри П. (2013). «Трехмерная граничная элементная формулировка несжимаемого вязкоупругого слоя конечной толщины, применяемая к сопротивлению качению жесткой сферы». International Journal of Solids and Structures . 50 (6): 833–842. doi : 10.1016/j.ijsolstr.2012.11.020 .
41. Зеиль, Жерар-Филипп; Гэвин, Анри П. (2013). «Простые алгоритмы решения стационарных задач фрикционного качения в двух и трех измерениях». Международный журнал твердых тел и структур . 50 (6): 843–852. doi : 10.1016/j.ijsolstr.2012.11.021 .
42. Зеиль, Жерар-Филипп; Гэвин, Анри П. (2013). «Упрощенные подходы к вязкоупругому сопротивлению качению». International Journal of Solids and Structures . 50 (6): 853–862. doi : 10.1016/j.ijsolstr.2012.09.025 .
43. Сина, Насер; Исфаханян, Вахид; Язди, Мохаммад Реза Хайри; Азади, Шахрам (18 апреля 2018 г.). "SAE MOBILUS". SAE International Journal of Passenger Cars - Mechanical Systems . 11 (2): 167–176. doi :10.4271/06-11-02-0014 . Получено 19 апреля 2021 г.
44. Сина, Насер; Хайри Язди, Мохаммад Реза; Эсфаханян, Вахид (2020-03-01). «Новый метод повышения энергоэффективности транспортного средства: минимизация потерь мощности шин». Труды Института инженеров-механиков, часть D: Журнал автомобильной инженерии . 234 (4): 1153–1166. doi :10.1177/0954407019861241. ISSN  0954-4070. S2CID  199099736.
45. Сина, Насер; Насири, Сайяд; Карханех, Вахид (2015-11-01). «Влияние резистивных нагрузок и давления в шинах на потери мощности в шинах и выбросы CO2 в реальных условиях». Applied Energy . 157 : 974–983. doi :10.1016/j.apenergy.2015.04.010. ISSN  0306-2619.
46. Сина, Насер; Исфаханян, Вахид; Язди, Мохаммад Реза Хайри; Азади, Шахрам (18 апреля 2018 г.). "SAE MOBILUS". SAE International Journal of Passenger Cars - Mechanical Systems . 11 (2): 167–176. doi :10.4271/06-11-02-0014 . Получено 19 апреля 2021 г.
47. Roberts, Рис. 17: «Влияние передачи крутящего момента на сопротивление качению», стр. 71
48. Деев, стр.30 включая уравнение (2.7) и рис. 2.3
49. Астахов, Рис. 3.8, 3.9, 3.11, стр. 50-55. Hay, Рис. 60-2, стр. 72 показывает те же явления, но имеет более высокие значения для Crr и не сообщается здесь, так как железные дороги в 2011 году [1]. заявляли о том же значении, что и Астахов
50. Херси, Таблица 6., стр. 267
51. Согласно этому предположению, где — сила сопротивления качению, а — нормальная сила нагрузки на колесо из-за веса транспортного средства, а — константа. Можно легко показать, дифференцируя по отношению к, используя это правило , что ${\displaystyle F=kN^{0.5}}$ ${\displaystyle F}$ ${\displaystyle N}$ ${\displaystyle k}$ ${\displaystyle F}$ ${\displaystyle N}$ ${\displaystyle {\operatorname {d} N \over N}=2{\operatorname {d} F \over F}}$
52. Робертс, стр. 60-61.
53. [2] Соотношение между давлением в шинах и силой сопротивления качению при разной скорости автомобиля | Апиват Суябодха | Кафедра автомобильной инженерии, Университет Рангсит, Лак-хок, Патхумтхани, Таиланд | 2017
54. Хоган, К. Майкл (1973). «Анализ шума на шоссе». Загрязнение воды, воздуха и почвы . 2 (3): 387–392. Bibcode : 1973WASP....2..387H. doi : 10.1007/BF00159677. S2CID  109914430.
55. Stachowiak, Gwidon W.; Batchelor, Andrew William (2000). Инженерная трибология (2-е изд.). Oxford: Butterworth-Heinemann. ISBN 978-0-7506-7304-4.
56. http://144.206.159.178/ft/200/607426/12614863.pdf ^{[ постоянная мертвая ссылка ]}
57. http://www.rubberchemtechnol.org/resource/1/rctea4/v3/i1/p19_s1?isAuthorized=no ^{[ постоянная мертвая ссылка ]}
58. «Шины Schwalbe: Сопротивление качению».
59. Информационный центр по лежачим велосипедам и транспортным средствам с человеческим приводом
60. Национальное бюро стандартов США, стр. ? и Уильямс, стр. ?
61. Робертс, «Влияние температуры», стр.59
62. Астахов, стр. 74, Хотя Астахов перечисляет эти компоненты, он не дает сумме названия.
63. Шадур. Л. А. (редактор). Вагоны (на русском языке) (Железнодорожные вагоны). Москва, Транспорт, 1980. С. 122 и рис. VI.1 п. 123 VI.2 с. 125
64. Ассоциация американских железных дорог, Механическое отделение "Энциклопедия вагонов и локомотивов", Нью-Йорк, Симмонс-Бордман, 1974. Раздел 14: "Шайбы и подшипники осей". Почти все объявления в этом разделе относятся к коническому типу подшипников.
65. Астахов, Рис 4.2, с. 76
66. Статистика железных дорог класса I в Соединенных Штатах, годы 1965-1975: Статистическое резюме. Вашингтон, округ Колумбия, Ассоциация американских железных дорог, Департамент экономики и финансов. См. таблицу для Amtrak, стр. 16. Чтобы получить тонны на пассажира, разделите тонно-мили (включая локомотивы) на пассажиро-мили. Чтобы получить тонно-брутто/тонно-нетто, разделите тонно-миль брутто (включая локомотивы) (в таблице "эксплуатационная статистика" на доходные тонно-мили (из таблицы "Грузовые перевозки")

• Астахов П.Н. (на русском языке) «Сопротивление движению железнодорожного подвижного состава» Труды ЦНИИ МПС (ISSN 0372-3305). Выпуск 311 (Том 311). - Москва: Транспорт, 1966. – 178 с. перм. запись в Калифорнийском университете в Беркли (в 2012 году полный текст был в Интернете, но в США был заблокирован)
• Деев В.В., Ильин Г.А., Афонин Г.С. (на русском языке) "Тяга поездов" Учебное пособие. - М.: Транспорт, 1987. - 264 с.
• Хей, Уильям У. «Железнодорожное машиностроение» Нью-Йорк, Wiley 1953
• Херси, Майо Д. , «Трение качения», Труды ASME , апрель 1969 г., стр. 260–275 и Журнал технологий смазывания , январь 1970 г., стр. 83–88 (одна статья, разделенная между двумя журналами). За исключением «Исторического введения» и обзора литературы, в основном речь идет о лабораторных испытаниях чугунных колес для рудничных железных дорог диаметром от 8 до 24 дюймов, проведенных в 1920-х годах (почти полувековая задержка между экспериментом и публикацией).
• Хорнер, Зигхард Ф., «Гидродинамическое сопротивление», опубликовано автором в 1965 г. (Глава 12 — «Наземные транспортные средства» и включает сопротивление качению (поезда, автомобили, грузовики).)
• Робертс, ГБ, «Потери мощности в шинах», Международная конференция по резине, Вашингтон, округ Колумбия, 1959 г.
• Национальное бюро стандартов США, «Механика пневматических шин», монография № 132, 1969–1970.
• Уильямс, JA Инженерная трибология. Oxford University Press, 1994.

Внешние ссылки

• Сопротивление качению и экономия топлива
• температура против сопротивления качению
• Простой тест на скатывание для измерения CRR в автомобилях и велосипедах
• Пороги сопротивления качению