Геодезические на эллипсоиде

Кратчайшие пути на ограниченной деформированной сферической поверхности второго порядка

Геодезическая на сплющенном эллипсоиде

Изучение геодезических на эллипсоиде возникло в связи с геодезией, в частности, с решением триангуляционных сетей . Фигура Земли хорошо аппроксимируется сплющенным эллипсоидом , слегка сплющенной сферой. Геодезическая — это кратчайший путь между двумя точками на искривленной поверхности, аналогичный прямой на плоской поверхности. Решение триангуляционной сети на эллипсоиде представляет собой, таким образом, набор упражнений по сфероидальной тригонометрии (Эйлер 1755).

Если рассматривать Землю как сферу , то геодезические линии представляют собой большие окружности (все из которых замкнуты), и проблемы сводятся к проблемам сферической тригонометрии . Однако Ньютон (1687) показал, что эффект вращения Земли приводит к тому, что она становится похожей на слегка сплющенный эллипсоид: в этом случае экватор и меридианы являются единственными простыми замкнутыми геодезическими. Более того, кратчайший путь между двумя точками на экваторе не обязательно проходит по экватору. Наконец, если эллипсоид еще больше возмущен, чтобы стать трехосным эллипсоидом (с тремя различными полуосями), замкнутыми будут только три геодезические.

Геодезические на эллипсоиде вращения

Существует несколько способов определения геодезических (Hilbert & Cohn-Vossen 1952, стр. 220–221). Простое определение — как кратчайший путь между двумя точками на поверхности. Однако часто бывает полезнее определять их как пути с нулевой геодезической кривизной — т. е. аналог прямых линий на искривленной поверхности. Это определение охватывает геодезические, проходящие так далеко по поверхности эллипсоида, что они начинают возвращаться к начальной точке, так что другие маршруты являются более прямыми, и включает пути, которые пересекаются или повторяют сами себя. Достаточно короткие сегменты геодезических по-прежнему являются кратчайшим путем между своими конечными точками, но геодезические не обязательно являются глобально минимальными (т. е. кратчайшими среди всех возможных путей). Каждый глобально кратчайший путь является геодезическим, но не наоборот.

К концу XVIII века эллипсоид вращения (также используется термин сфероид ) был общепринятым приближением к фигуре Земли . Корректировка сетей триангуляции повлекла за собой сведение всех измерений к опорному эллипсоиду и решение полученной двумерной задачи в качестве упражнения по сфероидальной тригонометрии (Бомфорд 1952, гл. 3) (Лейк и др. 2015, §4.5).

Рис. 1. Геодезическая AB на эллипсоиде вращения. N — северный полюс, а EFH лежит на экваторе.

Различные геодезические задачи можно свести к одному из двух типов. Рассмотрим две точки: A на широте φ ₁ и долготе λ ₁ и B на широте φ ₂ и долготе λ ₂ (см. рис. 1). Соединительная геодезическая (от A до B ) — это AB , длиной s ₁₂ , которая имеет азимуты α ₁ и α ₂ в двух конечных точках. ^[1] Обычно рассматриваются две геодезические задачи:

1. прямая геодезическая задача или первая геодезическая задача , заданные A , α ₁ и s ₁₂ , определяют B и α ₂ ;
2. обратная геодезическая задача или вторая геодезическая задача , при заданных A и B , определяет s ₁₂ , α ₁ и α ₂ .

Как видно из рис. 1, эти задачи включают решение треугольника NAB по одному углу, α ₁ для прямой задачи и λ ₁₂ = λ ₂ − λ ₁ для обратной задачи, и его двум смежным сторонам. Для сферы решения этих задач являются простыми упражнениями по сферической тригонометрии , решение которых дается формулами для решения сферического треугольника . (См. статью о навигации по большому кругу .)

Для эллипсоида вращения характеристическая постоянная, определяющая геодезическую, была найдена Клеро (1735). Систематическое решение для путей геодезических было дано Лежандром (1806) и Ориани (1806) (и последующими работами 1808 и 1810 годов). Полное решение прямой задачи (с вычислительными таблицами и разработанным примером) дано Бесселем (1825).

В XVIII веке геодезические линии обычно называли «кратчайшими линиями». Термин «геодезическая линия» (на самом деле, кривая ) был придуман Лапласом (1799b):

Nous désignerons cette ligne sous le nom de ligne géodesique [Мы назовем эту линию геодезической линией ].

Этот термин был введен в английский язык как «геодезическая линия» или как «геодезическая линия», например (Хаттон 1811, стр. 115),

Линия, проведенная описанным нами способом или выведенная из тригонометрических измерений указанными нами способами, называется геодезической или геодезической линией: она обладает тем свойством, что является кратчайшей линией, которую можно провести между ее двумя концами на поверхности Земли; и поэтому она является надлежащей мерой расстояния между этими двумя точками.

При принятии его в других областях науки предпочтение отдавалось геодезической линии , часто сокращаемой до геодезической .

В этом разделе рассматривается задача на эллипсоиде вращения (как сплющенном, так и вытянутом). Задача на трехосном эллипсоиде рассматривается в следующем разделе.

Уравнения геодезической

Здесь разрабатываются уравнения для геодезической; вывод близко следует выводу Бесселя (1825). Джордан и Эггерт (1941), Багратуни (1962, §15), Ганшин (1967, гл. 5), Кракивский и Томсон (1974, §4), Рапп (1993, §1.2), Джекели (2012) и Борре и Стрэнг (2012) также приводят выводы этих уравнений.

Рассмотрим эллипсоид вращения с экваториальным радиусом a и полярной полуосью b . Определим сплющивание f , эксцентриситет e и второй эксцентриситет e ′ :

${\displaystyle f={\frac {a-b}{a}},\quad e={\frac {\sqrt {a^{2}-b^{2}}}{a}}={\sqrt {f(2-f)}},\quad e'={\frac {\sqrt {a^{2}-b^{2}}}{b}}={\frac {e}{1-f}}.}$

(В большинстве приложений в геодезии эллипсоид считается сплюснутым, a > b ; однако эта теория применима без изменений к вытянутым эллипсоидам, a < b , и в этом случае f , e ² и e ′ ² отрицательны.)

Пусть элементарный отрезок пути на эллипсоиде имеет длину ds . Из рис. 2 и 3 видно, что если его азимут равен α , то ds связан с dφ и dλ соотношением

${\displaystyle \cos \alpha \,ds=\rho \,d\varphi =-{\frac {dR}{\sin \varphi }},\quad \sin \alpha \,ds=R\,d\lambda ,}$ (1)

где ρ — меридиональный радиус кривизны , R = ν cos φ — радиус круга широты φ , а ν — нормальный радиус кривизны . Элементарный сегмент, таким образом, задается как

${\displaystyle ds^{2}=\rho ^{2}\,d\varphi ^{2}+R^{2}\,d\lambda ^{2}}$

или

${\displaystyle {\begin{aligned}ds&={\sqrt {\rho ^{2}\varphi '^{2}+R^{2}}}\,d\lambda \\&\equiv L(\varphi ,\varphi ')\,d\lambda ,\end{aligned}}}$

где φ ′ = dφ / dλ и функция Лагранжа L зависит от φ через ρ( φ ) и R ( φ ) . Длина произвольного пути между ( φ ₁ , λ ₁ ) и ( φ ₂ , λ ₂ ) определяется как

${\displaystyle s_{12}=\int _{\lambda _{1}}^{\lambda _{2}}L(\varphi ,\varphi ')\,d\lambda ,}$

где φ — функция λ, удовлетворяющая φ ( λ ₁ ) = φ ₁ и φ ( λ ₂ ) = φ ₂ . Кратчайший путь или геодезическая влечет за собой нахождение той функции φ ( λ ), которая минимизирует s ₁₂ . Это упражнение по вариационному исчислению , а условие минимизации задается тождеством Бельтрами ,

${\displaystyle L-\varphi '{\frac {\partial L}{\partial \varphi '}}={\text{const.}}}$

Подставляя L и используя уравнения (1) , получаем

${\displaystyle R\sin \alpha ={\text{const.}}}$

Клеро (1735) нашел это соотношение , используя геометрическое построение; аналогичный вывод представлен Люстерником (1964, §10). ^[2] Дифференцирование этого соотношения дает

${\displaystyle d\alpha =\sin \varphi \,d\lambda .}$

Это, вместе с уравнениями (1) , приводит к системе обыкновенных дифференциальных уравнений для геодезической

${\displaystyle {\frac {d\varphi }{ds}}={\frac {\cos \alpha }{\rho }};\quad {\frac {d\lambda }{ds}}={\frac {\sin \alpha }{\nu \cos \varphi }};\quad {\frac {d\alpha }{ds}}={\frac {\tan \varphi \sin \alpha }{\nu }}.}$

Мы можем выразить R через параметрическую широту β , используя

${\displaystyle R=a\cos \beta ,}$

и отношение Клеро тогда становится

${\displaystyle \sin \alpha _{1}\cos \beta _{1}=\sin \alpha _{2}\cos \beta _{2}.}$

Это правило синусов сферической тригонометрии, связывающее две стороны треугольника NAB (см. рис. 4), NA = 1 ⁄ 2 π − β ₁ , и NB = 1 ⁄ 2 π − β ₂ , и их противолежащие углы B = π − α ₂ и A = α ₁ .

Чтобы найти соотношение для третьей стороны AB = σ ₁₂ , длины сферической дуги и прилежащего угла N = ω ₁₂ , сферической долготы , полезно рассмотреть треугольник NEP, представляющий геодезическую, начинающуюся на экваторе; см. рис. 5. На этом рисунке переменные, относящиеся к вспомогательной сфере, показаны с соответствующими величинами для эллипсоида, показанными в скобках. Величины без нижних индексов относятся к произвольной точке P ; E , точка, в которой геодезическая пересекает экватор в северном направлении, используется в качестве начала координат для σ , s и ω .

Рис. 6. Дифференциальный элемент геодезической на сфере.

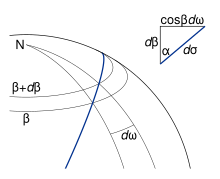
Если сторону EP расширить, перемещая P бесконечно мало (см. рис. 6), то получим

${\displaystyle \cos \alpha \,d\sigma =d\beta ,\quad \sin \alpha \,d\sigma =\cos \beta \,d\omega .}$ (2)

Объединение уравнений (1) и (2) дает дифференциальные уравнения для s и λ

${\displaystyle {\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\frac {\sin \beta }{\sin \varphi }}.}$

Соотношение между β и φ следующее:

${\displaystyle \tan \beta ={\sqrt {1-e^{2}}}\tan \varphi =(1-f)\tan \varphi ,}$

что дает

${\displaystyle {\frac {\sin \beta }{\sin \varphi }}={\sqrt {1-e^{2}\cos ^{2}\beta }},}$

так что дифференциальные уравнения для геодезической становятся

${\displaystyle {\frac {1}{a}}{\frac {ds}{d\sigma }}={\frac {d\lambda }{d\omega }}={\sqrt {1-e^{2}\cos ^{2}\beta }}.}$

Последний шаг — использовать σ как независимый параметр в обоих этих дифференциальных уравнениях и тем самым выразить s и λ как интегралы. Применение правила синусов к вершинам E и G в сферическом треугольнике EGP на рис. 5 дает

${\displaystyle \sin \beta =\sin \beta (\sigma ;\alpha _{0})=\cos \alpha _{0}\sin \sigma ,}$

где α ₀ — азимут в точке E. Подставляя это в уравнение для ds / d σ и интегрируя результат, получаем

${\displaystyle {\frac {s}{b}}=\int _{0}^{\sigma }{\sqrt {1+k^{2}\sin ^{2}\sigma '}}\,d\sigma ',}$ (3)

где

${\displaystyle k=e'\cos \alpha _{0},}$

и пределы интеграла выбираются так, что s ( σ = 0) = 0 . Лежандр (1811, стр. 180) указал, что уравнение для s такое же, как уравнение для дуги эллипса с полуосями b √ 1 + e ′ ² cos ² α ₀ и b . Чтобы выразить уравнение для λ через σ , запишем

${\displaystyle d\omega ={\frac {\sin \alpha _{0}}{\cos ^{2}\beta }}\,d\sigma ,}$

что следует из уравнения 2 и соотношения Клеро. Это дает

${\displaystyle \lambda -\lambda _{0}=\omega -f\sin \alpha _{0}\int _{0}^{\sigma }{\frac {2-f}{1+(1-f){\sqrt {1+k^{2}\sin ^{2}\sigma '}}}}\,d\sigma ',}$ (4)

и пределы интегралов выбираются так, что λ = λ ₀ при пересечении экватора, σ = 0 .

Это завершает решение пути геодезической с использованием вспомогательной сферы. С помощью этого устройства большой круг может быть точно отображен на геодезическую на эллипсоиде вращения.

Существует также несколько способов аппроксимации геодезических на земном эллипсоиде (с небольшим сплющиванием) (Rapp 1991, §6); некоторые из них описаны в статье о географическом расстоянии . Однако они, как правило, сопоставимы по сложности с методом точного решения (Jekeli 2012, §2.1.4).

Поведение геодезических линий

Рис. 7. Меридианы и экватор являются единственными замкнутыми геодезическими. (Для очень сплющенных эллипсоидов существуют другие замкнутые геодезические; см. рис. 11 и 12).

Геодезическая на сплющенном эллипсоиде ( f = 1 ⁄ 50 ) с α ₀ =45° .

Рис. 10. Геодезическая на вытянутом эллипсоиде ( f = − 1 ⁄ 50 ) с α ₀ =45° . Сравните с рис. 8.

На рис. 7 показаны простые замкнутые геодезические, которые состоят из меридианов (зеленые) и экватора (красные). (Здесь определение «простые» означает, что геодезические замыкаются на себя без промежуточного самопересечения.) Это следует из уравнений для геодезических, приведенных в предыдущем разделе.

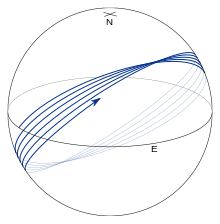
Все остальные геодезические проиллюстрированы на рис. 8 и 9, на которых показана геодезическая, начинающаяся на экваторе с α ₀ = 45° . Геодезическая колеблется вокруг экватора. Экваториальные пересечения называются узлами , а точки максимальной или минимальной широты называются вершинами ; параметрические широты вершин задаются как β = ±( 1 ⁄ 2 π − |α ₀ |) . Геодезическая завершает одно полное колебание по широте до того, как долгота увеличится на360° . Таким образом, при каждом последующем пересечении экватора на север (см. рис. 8) λ не дотягивает до полного оборота экватора примерно на 2 π f sinα ₀ (для вытянутого эллипсоида эта величина отрицательна, и λ совершает более одного полного оборота; см. рис. 10). Почти для всех значений α ₀ геодезическая заполнит ту часть эллипсоида, которая находится между двумя широтами вершин (см. рис. 9).

Две дополнительные замкнутые геодезические для сплюснутого эллипсоида, b ⁄ a = 2 ⁄ 7 .

Если эллипсоид достаточно сплющен, т. е. b ⁄ a < 1 ⁄ 2 , возможен другой класс простых замкнутых геодезических (Клингенберг 1982, §3.5.19). Две такие геодезические показаны на рис. 11 и 12. Здесь b ⁄ a = 2 ⁄ 7 и экваториальный азимут, α ₀ , для зеленой (соответственно синей) геодезической выбран равным53.175° (соотв.75,192° ), так что геодезическая совершает 2 (соответственно 3) полных колебания вокруг экватора за один оборот эллипсоида.

Рис. 13. Геодезические (синие) из одной точки для f = 1 ⁄ 10 , φ ₁ =−30° ; геодезические окружности показаны зеленым цветом, а место сечения — красным.

На рис. 13 показаны геодезические (синего цвета), исходящие из точки А с α ₁ кратным15° до точки, в которой они перестают быть кратчайшими путями. (Сглаживание было увеличено до 1 ⁄ 10 , чтобы подчеркнуть эллипсоидальные эффекты.) Также показаны (зеленым цветом) кривые постоянной s ₁₂ , которые являются геодезическими окружностями с центром в точке A . Гаусс (1828) показал, что на любой поверхности геодезические и геодезические окружности пересекаются под прямым углом.

Красная линия — это разрезное место , место точек, которые имеют несколько (в данном случае две) кратчайших геодезических из A. На сфере разрезное место — это точка. На сплющенном эллипсоиде (показанном здесь) это сегмент круга широты с центром в точке, антиподальной к A , φ = − φ ₁ . Продольная протяженность разрезного места приблизительно равна λ ₁₂ ∈ [ π (1 − f cos φ ₁ ), π (1 + f cos φ ₁ )] . Если A лежит на экваторе, φ ₁ = 0 , это соотношение является точным, и, как следствие, экватор является кратчайшей геодезической, только если | λ ₁₂ | ≤ π (1 − f ) . Для вытянутого эллипсоида точкой разреза является отрезок антимеридиана с центром в точке, антиподальной к A , λ ₁₂ = π , и это означает, что меридиональные геодезические перестают быть кратчайшими путями до того, как будет достигнута антиподальная точка.

Дифференциальные свойства геодезических

Различные проблемы, связанные с геодезическими, требуют знания их поведения при возмущении. Это полезно в тригонометрических корректировках (Ehlert 1993), определении физических свойств сигналов, которые следуют за геодезическими и т. д. Рассмотрим опорную геодезическую, параметризованную s , и вторую геодезическую на небольшом расстоянии t ( s ) от нее. Гаусс (1828) показал, что t ( s ) подчиняется уравнению Гаусса-Якоби

${\displaystyle {\frac {d^{2}t(s)}{ds^{2}}}+K(s)t(s)=0,}$

Рис. 14. Определение приведенной длины и геодезического масштаба.

где K ( s ) — гауссова кривизна в точке s . Как линейное однородное дифференциальное уравнение второго порядка, его решение может быть выражено как сумма двух независимых решений

${\displaystyle t(s_{2})=Cm(s_{1},s_{2})+DM(s_{1},s_{2})}$

где

${\displaystyle {\begin{aligned}m(s_{1},s_{1})&=0,\quad \left.{\frac {dm(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=1,\\M(s_{1},s_{1})&=1,\quad \left.{\frac {dM(s_{1},s_{2})}{ds_{2}}}\right|_{s_{2}=s_{1}}=0.\end{aligned}}}$

Величина m ( s ₁ , s ₂ ) = m ₁₂ является так называемой приведенной длиной , а M ( s ₁ , s ₂ ) = M ₁₂ является геодезическим масштабом . ^[3] Их основные определения проиллюстрированы на рис. 14.

Гауссова кривизна для эллипсоида вращения равна

${\displaystyle K={\frac {1}{\rho \nu }}={\frac {{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}{b^{2}}}={\frac {b^{2}}{a^{4}{\bigl (}1-e^{2}\cos ^{2}\beta {\bigr )}^{2}}}.}$

Гельмерт (1880, уравнение (6.5.1.)) решил уравнение Гаусса-Якоби для этого случая, что позволило выразить m ₁₂ и M _{12 в виде интегралов.}

Как мы видим из рис. 14 (верхний подрисунок), разделение двух геодезических, начинающихся в одной точке с азимутами, отличающимися на d α _{1 ,} равно m ₁₂ d α ₁ . На замкнутой поверхности, такой как эллипсоид, m ₁₂ колеблется около нуля. Точка, в которой m ₁₂ становится равным нулю, является точкой, сопряженной начальной точке. Для того чтобы геодезическая между A и B , длиной s ₁₂ , была кратчайшим путем, она должна удовлетворять условию Якоби (Якоби 1837) (Якоби 1866, §6) (Форсайт 1927, §§26–27) (Блисс 1916), что между A и B нет точки, сопряженной с A . Если это условие не выполняется, то есть соседний путь (не обязательно геодезический), который короче. Таким образом, условие Якоби является локальным свойством геодезической и является лишь необходимым условием для того, чтобы геодезическая была глобальным кратчайшим путем. Необходимые и достаточные условия для того, чтобы геодезическая была кратчайшим путем:

• для сплюснутого эллипсоида, | σ ₁₂ | ≤ π ;
• для вытянутого эллипсоида, | λ ₁₂ | ≤ π , если α ₀ ≠ 0 ; если α ₀ = 0 , дополнительное условие m ₁₂ ≥ 0 требуется, если | λ ₁₂ | = π .

Оболочка геодезических линий

Геодезические из одной точки ( f = 1 ⁄ 10 , φ ₁ =−30° )

Геодезические из определенной точки A, если их продолжить за пределы сечения, образуют огибающую, показанную на рис. 15. Здесь геодезические, для которых α ₁ кратно3° показаны светло-голубым цветом. (Геодезические показаны только для их первого прохождения вблизи антиподальной точки, а не для последующих.) Некоторые геодезические окружности показаны зеленым цветом; они образуют выступы на оболочке. Геометрическое место точек разреза показано красным цветом. Оболочка является геометрическим местом точек, которые сопряжены с A ; точки на оболочке могут быть вычислены путем нахождения точки, в которой m ₁₂ = 0 на геодезической. Якоби (1891) называет эту звездообразную фигуру, созданную оболочкой, астроидой .

Снаружи астроиды две геодезические пересекаются в каждой точке; таким образом, между A и этими точками есть две геодезические (длиной примерно в половину окружности эллипсоида) . Это соответствует ситуации на сфере, где есть «короткие» и «длинные» пути на большом круге между двумя точками. Внутри астроиды четыре геодезические пересекаются в каждой точке. Четыре такие геодезические показаны на рис. 16, где геодезические пронумерованы в порядке возрастания длины. (Этот рисунок использует то же положение для A , что и рис. 13, и нарисован в той же проекции.) Две более короткие геодезические устойчивы , т. е. m ₁₂ > 0 , так что нет соседнего пути, соединяющего две точки, который короче; другие два неустойчивы. Только самая короткая линия (первая) имеет σ ₁₂ ≤ π . Все геодезические касаются оболочки, которая показана зеленым на рисунке.

Астроида является (внешней) эволютой геодезических окружностей с центром в точке A. Аналогично, геодезические окружности являются эволютами астроиды.

Площадь геодезического многоугольника

Геодезический многоугольник — это многоугольник, стороны которого являются геодезическими. Он аналогичен сферическому многоугольнику , стороны которого являются большими окружностями. Площадь такого многоугольника можно найти, сначала вычислив площадь между геодезическим сегментом и экватором, т. е. площадь четырехугольника AFHB на рис. 1 (Danielsen 1989). Как только эта площадь известна, площадь многоугольника можно вычислить, суммируя вклады всех ребер многоугольника.

Здесь выражение для площади S ₁₂ AFHB разработано в соответствии с Sjöberg (2006). Площадь любой замкнутой области эллипсоида равна

${\displaystyle T=\int dT=\int {\frac {1}{K}}\cos \varphi \,d\varphi \,d\lambda ,}$

где dT — элемент площади поверхности, а K — гауссова кривизна . Теперь теорема Гаусса–Бонне, примененная к геодезическому многоугольнику, утверждает

${\displaystyle \Gamma =\int K\,dT=\int \cos \varphi \,d\varphi \,d\lambda ,}$

где

${\displaystyle \Gamma =2\pi -\sum _{j}\theta _{j}}$

— геодезический избыток, а θ _j — внешний угол при вершине j . Умножая уравнение для Γ на R ₂ ² , где R ₂ — аутентичный радиус , и вычитая это из уравнения для T, получаем

${\displaystyle {\begin{aligned}T&=R_{2}^{2}\,\Gamma +\int \left({\frac {1}{K}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda \\&=R_{2}^{2}\,\Gamma +\int \left({\frac {b^{2}}{{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}^{2}}}-R_{2}^{2}\right)\cos \varphi \,d\varphi \,d\lambda ,\end{aligned}}}$

где было подставлено значение K для эллипсоида . Применяя эту формулу к четырехугольнику AFHB , отмечая, что Γ = α ₂ − α ₁ , и выполняя интеграл по φ, получаем

${\displaystyle S_{12}=R_{2}^{2}(\alpha _{2}-\alpha _{1})+b^{2}\int _{\lambda _{1}}^{\lambda _{2}}\left({\frac {1}{2{\bigl (}1-e^{2}\sin ^{2}\varphi {\bigr )}}}+{\frac {\tanh ^{-1}(e\sin \varphi )}{2e\sin \varphi }}-{\frac {R_{2}^{2}}{b^{2}}}\right)\sin \varphi \,d\lambda ,}$

где интеграл берется по геодезической линии (так что φ неявно является функцией λ ). Интеграл можно выразить в виде ряда, справедливого для малых f (Danielsen 1989) (Karney 2013, §6 и приложение).

Площадь геодезического многоугольника определяется суммированием S ₁₂ по его ребрам. Этот результат справедлив при условии, что многоугольник не включает полюс; если он включает, то к сумме необходимо добавить 2 π R ₂ ^2. Если ребра заданы их вершинами, то удобное выражение для геодезического избытка E ₁₂ = α ₂ − α ₁ имеет вид

${\displaystyle \tan {\frac {E_{12}}{2}}={\frac {\sin {\tfrac {1}{2}}(\beta _{2}+\beta _{1})}{\cos {\tfrac {1}{2}}(\beta _{2}-\beta _{1})}}\tan {\frac {\omega _{12}}{2}}.}$

Решение прямой и обратной задачи

Решение геодезических задач влечет за собой отображение геодезической на вспомогательную сферу и решение соответствующей задачи в навигации по большому кругу . При решении «элементарного» сферического треугольника для NEP на рис. 5 можно использовать правила Непера для квадрантных треугольников ,

${\displaystyle {\begin{aligned}\sin \alpha _{0}&=\sin \alpha \cos \beta =\tan \omega \cot \sigma ,\\\cos \sigma &=\cos \beta \cos \omega =\tan \alpha _{0}\cot \alpha ,\\\cos \alpha &=\cos \omega \cos \alpha _{0}=\cot \sigma \tan \beta ,\\\sin \beta &=\cos \alpha _{0}\sin \sigma =\cot \alpha \tan \omega ,\\\sin \omega &=\sin \sigma \sin \alpha =\tan \beta \tan \alpha _{0}.\end{aligned}}}$

Картографирование геодезической включает оценку интегралов для расстояния s и долготы λ , уравнения (3) и (4) , которые зависят от параметра α ₀ .

Решение прямой задачи не вызывает затруднений, поскольку α ₀ можно определить непосредственно из заданных величин φ ₁ и α ₁ ; пример расчета см. в работе Карни (2013).

В случае обратной задачи λ ₁₂ задано; это не может быть легко связано с эквивалентным сферическим углом ω _12, поскольку α ₀ неизвестен. Таким образом, решение задачи требует, чтобы α ₀ находили итеративно ( нахождение корня ); подробности см. в Karney (2013).

В геодезических приложениях, где f мало, интегралы обычно вычисляются как ряды (Legendre 1806) (Oriani 1806) (Bessel 1825) (Helmert 1880) (Rainsford 1955) (Rapp 1993). Для произвольного f интегралы (3) и (4) можно найти с помощью числовой квадратуры или выразив их через эллиптические интегралы (Legendre 1806) (Cayley 1870) (Karney 2024).

Винсенти (1975) предлагает решения для прямой и обратной задач; они основаны на разложении в ряд, выполненном до третьего порядка при выравнивании, и обеспечивают точность около0,1 мм для эллипсоида WGS84 ; однако обратный метод не сходится для почти антиподных точек.

Карни (2013) продолжает разложения до шестого порядка, что достаточно для обеспечения полной двойной точности для | f | ≤ 1 ⁄ 50 и улучшает решение обратной задачи, так что оно сходится во всех случаях. Карни (2013, приложение) расширяет метод для использования эллиптических интегралов, которые можно применять к эллипсоидам с произвольным сплющиванием.

Геодезические на трехосном эллипсоиде

Решение геодезической задачи для эллипсоида вращения математически просто: из-за симметрии геодезические имеют постоянную движения , заданную соотношением Клеро, что позволяет свести задачу к квадратуре . К началу 19 века (благодаря работам Лежандра , Ориани , Бесселя и др.) было достигнуто полное понимание свойств геодезических на эллипсоиде вращения.

С другой стороны, геодезические на трехосном эллипсоиде (с тремя неравными осями) не имеют очевидной константы движения и, таким образом, представляли собой сложную нерешенную проблему в первой половине 19 века. В замечательной статье Якоби (1839) открыл константу движения, позволяющую свести эту задачу к квадратуре (Клингенберг 1982, §3.5). ^[4]

Система координат трехосного эллипсоида

Рис. 17. Трехосные эллипсоидальные координаты.

Рассмотрим эллипсоид, определяемый формулой

${\displaystyle h={\frac {X^{2}}{a^{2}}}+{\frac {Y^{2}}{b^{2}}}+{\frac {Z^{2}}{c^{2}}}=1,}$

где ( X , Y , Z ) — декартовы координаты с центром на эллипсоиде и, без потери общности, a ≥ b ≥ c > 0. [ ^5]Якоби (1866, §§26–27) использовал (триаксиальные) эллипсоидальные координаты (с триаксиальной эллипсоидальной широтой и триаксиальной эллипсоидальной долготой , β , ω ), определяемые как

${\displaystyle {\begin{aligned}X&=a\cos \omega {\frac {\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {a^{2}-c^{2}}}},\\Y&=b\cos \beta \sin \omega ,\\Z&=c\sin \beta {\frac {\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {a^{2}-c^{2}}}}.\end{aligned}}}$

В пределе b → a , β становится параметрической широтой для сплющенного эллипсоида, поэтому использование символа β согласуется с предыдущими разделами. Однако ω отличается от сферической долготы, определенной выше. [ ^6]

Линии сетки постоянной β (синим цветом) и ω (зеленым цветом) показаны на рис. 17. Они образуют ортогональную систему координат: линии сетки пересекаются под прямым углом. Главные сечения эллипсоида, определяемые X = 0 и Z = 0, показаны красным цветом. Третье главное сечение, Y = 0 , покрыто линиями β = ±90° и ω = 0° или ±180° . Эти линии встречаются в четырех точках умбилики (две из которых видны на этом рисунке), где главные радиусы кривизны равны. Здесь и на других рисунках в этом разделе параметры эллипсоида равны a : b : c = 1,01:1:0,8 , и он рассматривается в ортогональной проекции из точки выше φ = 40° , λ = 30° .

Линии сетки эллипсоидальных координат можно интерпретировать тремя различными способами:

1. Они являются «линиями кривизны» на эллипсоиде: они параллельны направлениям главной кривизны (Монж, 1796).
2. Они также являются пересечениями эллипсоида с софокусными системами однополостных и двуполостных гиперболоидов (Дюпен 1813, часть 5).
3. Наконец, это геодезические эллипсы и гиперболы, определяемые с помощью двух соседних точек пупка (Hilbert & Cohn-Vossen 1952, стр. 188). Например, линии постоянной β на рис. 17 могут быть получены с помощью знакомой конструкции струны для эллипсов с концами струны, прикрепленными к двум точкам пупка.

Решение Якоби

Якоби показал, что геодезические уравнения, выраженные в эллипсоидальных координатах, являются разделимыми. Вот как он рассказал о своем открытии своему другу и соседу Бесселю (Якоби 1839, Письмо Бесселю),

Позавчера я свел к квадратуре задачу геодезических линий на эллипсоиде с тремя неравными осями . Это простейшие формулы в мире, абелевы интегралы , которые становятся известными эллиптическими интегралами, если две оси сделать равными.

Кёнигсберг , 28 декабря 1938 года.

Решение, данное Якоби (Якоби 1839) (Якоби 1866, §28), следующее:

${\displaystyle {\begin{aligned}\delta &=\int {\frac {{\sqrt {b^{2}\sin ^{2}\beta +c^{2}\cos ^{2}\beta }}\,d\beta }{{\sqrt {a^{2}-b^{2}\sin ^{2}\beta -c^{2}\cos ^{2}\beta }}{\sqrt {{\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta -\gamma }}}}\\[6pt]&\quad -\int {\frac {{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega }}\,d\omega }{{\sqrt {a^{2}\sin ^{2}\omega +b^{2}\cos ^{2}\omega -c^{2}}}{\sqrt {{\bigl (}a^{2}-b^{2}{\bigr )}\sin ^{2}\omega +\gamma }}}}.\end{aligned}}}$

Как отмечает Якоби, «функция угла β равна функции угла ω . Эти две функции являются просто абелевыми интегралами...» В решении появляются две константы δ и γ . Обычно δ равно нулю, если нижние пределы интегралов принимаются за начальную точку геодезической, а направление геодезических определяется γ . Однако для геодезических, начинающихся в точках пупочной области, мы имеем γ = 0 , а δ определяет направление в точке пупочной области. Константа γ может быть выражена как

${\displaystyle \gamma ={\bigl (}b^{2}-c^{2}{\bigr )}\cos ^{2}\beta \sin ^{2}\alpha -{\bigl (}a^{2}-b^{2}{\bigl )}\sin ^{2}\omega \cos ^{2}\alpha ,}$

где α — угол, который геодезическая образует с линиями постоянной ω . В пределе b → a это сводится к sinα cos β = const. , известному соотношению Клеро. Вывод результата Якоби дан Дарбу (1894, §§583–584); он приводит решение, найденное Лиувиллем (1846) для общих квадратичных поверхностей.

Обследование трехосных геодезических

Циркумполярные геодезические, ω ₁ =0° , α ₁ =90° .

На трехосном эллипсоиде есть только три простые замкнутые геодезические, три главных сечения эллипсоида, заданные как X = 0 , Y = 0 и Z = 0 . ^[7] Для обзора других геодезических удобно рассматривать геодезические, которые пересекают среднее главное сечение, Y = 0 , под прямым углом. Такие геодезические показаны на рис. 18–22, которые используют те же параметры эллипсоида и то же направление взгляда, что и рис. 17. Кроме того, три главных эллипса показаны красным на каждом из этих рисунков.

Если начальная точка β ₁ ∈ (−90°, 90°) , ω ₁ = 0 и α ₁ = 90° , то γ > 0 и геодезическая охватывает эллипсоид в «циркумполярном» смысле. Геодезическая колеблется к северу и югу от экватора; при каждом колебании она совершает немного меньший полный оборот вокруг эллипсоида, в результате чего в типичном случае геодезическая заполняет область, ограниченную двумя линиями широты β = ± β ₁ . На рис. 18 и 19 приведены два примера. Рисунок 18 показывает практически то же поведение, что и для сплющенного эллипсоида вращения (потому что a ≈ b ); сравните с рис. 9. Однако, если начальная точка находится на более высокой широте (рис. 18), искажения, возникающие из-за a ≠ b, очевидны. Все касательные к циркумполярной геодезической касаются конфокального однополостного гиперболоида, который пересекает эллипсоид в точке β = β ₁ (Chasles 1846) (Hilbert & Cohn-Vossen 1952, стр. 223–224).

Трансполярная геодезическая, β ₁ =90° , α ₁ =180° .

Если начальная точка β ₁ = 90° , ω ₁ ∈ (0°, 180°) и α ₁ = 180° , то γ < 0 и геодезическая охватывает эллипсоид в «трансполярном» смысле. Геодезическая колеблется на восток и запад от эллипса X = 0 ; при каждом колебании она совершает немного больше полного оборота вокруг эллипсоида. В типичном случае это приводит к тому, что геодезическая заполняет область, ограниченную двумя линиями долготы ω = ω ₁ и ω = 180° − ω ₁ . Если a = b , все меридианы являются геодезическими; эффект a ≠ b заставляет такие геодезические колебаться на восток и запад. Два примера приведены на рис. 20 и 21. Сужение геодезической вблизи полюса исчезает в пределе b → c ; в этом случае эллипсоид становится вытянутым эллипсоидом и рис. 20 будет напоминать рис. 10 (повернутый на бок). Все касательные к трансполярной геодезической касаются конфокального двухполостного гиперболоида, который пересекает эллипсоид в точке ω = ω ₁ .

На рис. 18–21 геодезические (почти) замкнуты. Как отмечено выше, в типичном случае геодезические не замкнуты, а заполняют область, ограниченную предельными линиями широты (в случае рис. 18–19) или долготы (в случае рис. 20–21).

Рис. 22. Геодезическая омбиликальная линия, β ₁ =90° , ω ₁ =0° , α ₁ =135° .

Если начальная точка β ₁ = 90° , ω ₁ = 0° (точка пупка) и α ₁ = 135° (геодезическая линия покидает эллипс Y = 0 под прямым углом), то γ = 0 и геодезическая линия многократно пересекает противоположную точку пупка и возвращается в свою начальную точку. Однако на каждом витке угол, под которым она пересекает Y = 0, становится ближе к0° или180° , так что асимптотически геодезическая лежит на эллипсе Y = 0 (Hart 1849) (Arnold 1989, стр. 265), как показано на рис. 22. Одна геодезическая не заполняет область на эллипсоиде. Все касательные к омбилическим геодезическим касаются конфокальной гиперболы, которая пересекает эллипсоид в омбилических точках.

Геодезические пуповины обладают несколькими интересными свойствами.

• Через любую точку эллипсоида проходят две омбиликальные геодезические.
• Геодезическое расстояние между противоположными пупочными точками одинаково независимо от начального направления геодезической.
• В то время как замкнутые геодезические на эллипсах X = 0 и Z = 0 устойчивы (геодезическая, изначально близкая к эллипсу и почти параллельная ему, остается близкой к эллипсу), замкнутая геодезическая на эллипсе Y = 0 , которая проходит через все 4 точки пупка, экспоненциально неустойчива . Если ее возмущение, она выйдет из плоскости Y = 0 и перевернется, прежде чем вернуться близко к плоскости. (Это поведение может повторяться в зависимости от характера начального возмущения.)

Если начальная точка A геодезической не является точкой пупка, то ее огибающая является астроидой с двумя точками возврата, лежащими на β = − β ₁ , а двумя другими на ω = ω ₁ + π . Точкой разреза для A является часть линии β = − β ₁ между точками возврата.

Приложения

Прямые и обратные геодезические задачи больше не играют той центральной роли в геодезии, как когда-то. Вместо решения уравнивания геодезических сетей как двумерной задачи сфероидальной тригонометрии, эти задачи теперь решаются трехмерными методами (Vincenty & Bowring 1978). Тем не менее, наземная геодезическая система по-прежнему играет важную роль в нескольких областях:

• для измерения расстояний и площадей в географических информационных системах ;
• определение морских границ (UNCLOS 2006);
• в правилах Федерального управления гражданской авиации по зональной навигации (RNAV 2007);
• метод измерения расстояний в Спортивном кодексе ФАИ (FAI 2018).
• помогите мусульманам найти направление к Мекке

По принципу наименьшего действия многие проблемы в физике можно сформулировать как вариационную задачу, похожую на задачу для геодезических. Действительно, геодезическая задача эквивалентна движению частицы, вынужденной двигаться по поверхности, но в остальном не подверженной никаким силам (Лаплас 1799a) (Гильберт и Кон-Фоссен 1952, стр. 222). По этой причине геодезические на простых поверхностях, таких как эллипсоиды вращения или трехосные эллипсоиды, часто используются в качестве «тестовых случаев» для исследования новых методов. Вот некоторые примеры:

• разработка эллиптических интегралов (Лежандр 1811) и эллиптических функций (Вейерштрасс 1861);
• развитие дифференциальной геометрии (Гаусс 1828) (Кристоффель 1869);
• методы решения систем дифференциальных уравнений путем замены независимых переменных (Якоби 1839);
• изучение каустики (Якоби 1891);
• исследования числа и устойчивости периодических орбит (Пуанкаре, 1905);
• в пределе c → 0 геодезические на трехосном эллипсоиде сводятся к случаю динамических бильярдов ;
• расширения до произвольного числа измерений (Кнёррер, 1980);
• геодезический поток на поверхности (Бергер 2010, гл. 12).

Смотрите также

• Пути земного сечения
• Фигура Земли
• Географическое расстояние
• Навигация по дуге большого круга
• Большой эллипс
• Геодезический
• Геодезия
• Проекция карты
  • Картографическая проекция трехосного эллипсоида
• Дуга меридиана
• Локсодромальная линия
• Формулы Винсента

Примечания

1. Здесь α ₂ — прямой азимут в точке B. Некоторые авторы вместо этого вычисляют обратный азимут; он задается как α ₂ ± π .
2. Лаплас (1799a) показал, что частица, вынужденная двигаться по поверхности, но не подверженная никаким другим силам, движется вдоль геодезической линии этой поверхности. Таким образом, соотношение Клеро является просто следствием сохранения момента импульса для частицы на поверхности вращения.
3. Багратуни (1962, §17) использует термин «коэффициент сходимости ординат» для геодезической шкалы.
4. Этот раздел адаптирован из документации GeographicLib (Karney 2015, Geodesics on a triaxial ellipsoid)
5. Это обозначение для полуосей несовместимо с тем, которое использовалось в предыдущем разделе об эллипсоидах вращения, в котором a и b обозначали экваториальный радиус и полярную полуось. Таким образом, соответствующие неравенства имеют вид a = a ≥ b > 0 для сплюснутого эллипсоида и b ≥ a = a > 0 для вытянутого эллипсоида.
6. Предел b → c дает вытянутый эллипсоид, где ω играет роль параметрической широты.
7. Если c ⁄ a < 1 ⁄ 2 , существуют другие простые замкнутые геодезические, подобные показанным на рис. 11 и 12 (Клингенберг 1982, §3.5.19).

Ссылки

• Арнольд, VI (1989). Математические методы классической механики . Перевод Фогтмана, К.; Вайнштейна, А. (2-е изд.). Springer-Verlag. ISBN 978-0-387-96890-2. OCLC  4037141.
• Багратуни, Г. В. (1967) [1962]. Курс сфероидальной геодезии . дои : 10.5281/zenodo.32371. ОСЛК  6150611.Перевод с русского языка Курса сфероидной геодезии (Москва, 1962 г.) ВВС США (FTD-MT-64-390)
• Бергер, М. (2010). Раскрытая геометрия . Перевод Сенечала, Л. Дж. Спрингера. doi : 10.1007/978-3-540-70997-8. ISBN 978-3-540-70996-1.
• Бессель, Ф. В. (2010) [1825]. «Вычисление долготы и широты по геодезическим измерениям». Astronomische Nachrichten . 331 (8). Перевод Karney, CFF; Deakin, RE: 852–861. arXiv : 0908.1824 . Bibcode : 2010AN....331..852K. doi : 10.1002/asna.201011352. S2CID  118760590.Английский перевод Astron. Nachr. 4, 241–254 (1825). Опечатки.
• Блисс, GA (1916). «Условие Якоби для задач вариационного исчисления в параметрической форме». Труды Американского математического общества . 17 (2): 195–206. doi : 10.1090/S0002-9947-1916-1501037-4 .
• Бомфорд, Г. (1952). Геодезия . Оксфорд: Кларендон. OCLC  1396190.
• Борре, К.; Стрэнг, В. Г. (2012). "11, Геометрия эллипсоида" (PDF) . Алгоритмы глобального позиционирования . Wellesley-Cambridge Press. ISBN 978-0-9802327-3-8. OCLC  795014501.
• Кэли, А. (1870). «О геодезических линиях на сплющенном сфероиде». Philosophical Magazine . 4-я серия. 40 (268): 329–340. doi :10.1080/14786447008640411.
• Часлз, М. (1846). «Sur les lignes géodesiques et les lignes de Courbure des Surfaces du Second Degree» [Геодезические линии и линии кривизны поверхностей второй степени]. Journal de Mathématiques Pures et Appliquées (на французском языке). 11 :5–20.PDF-файл.
• Кристоффель, Э.Б. (1869). «Allgemeine Theorie der geodätischen Driecke» [Общая теория геодезических треугольников]. Abhandlungen Königlichen Akademie der Wissenschaft zu Berlin (на немецком языке): 119–176.
• Клеро, AC (1735 г.). «Détermination géometrique de la perpendiculaire à la méridienne tracée par M. Cassini» [Геометрическое определение перпендикуляра к меридиану, проведенного Жаком Кассини]. Mémoires de l'Académie Royale des Sciences de Paris 1733 (на французском языке): 406–416.
• Danielsen, JS (1989). «Площадь под геодезической». Survey Review . 30 (232): 61–66. doi :10.1179/003962689791474267.
• Дарбу, JG (1894). Leçons sur la théorie générale des Surfaces [ Уроки общей теории поверхностей ] (на французском языке). Том. 3. Париж: Готье-Виллар. ОСЛК  8566228.
• Дюпен, ПКФ (1813). Développements de Géométrie [ Развития геометрии ] (на французском языке). Париж: Курьер. ОСЛК  560800801.
• Элерт, Д. (1993). Methoden der ellipsoidischen Dreiecksberechnung [ Методы эллипсоидальной триангуляции ] (Технический отчет). Рейхе Б: Angewandte Geodäsie, Heft Nr. 292 (на немецком языке). Немецкая геодезическая комиссия. ОСЛК  257615376.
• Эйлер, Л. (1755). «Élémens de la trigonométrie sphéroïdique tirés de la méthode des plus grands et plus petits» [Элементы сфероидальной тригонометрии, взятые из метода максимумов и минимумов]. Mémoires de l'Académie Royale des Sciences de Berlin, 1753 г. (на французском языке). 9 : 258–293.Цифры.
• ФАИ (2018). «Раздел 8.2.3». Спортивный кодекс ФАИ (PDF) (Технический отчет). Лозанна, Швейцария: Международная авиационная федерация.
• Форсайт, AR (1927). Вариационное исчисление . Cambridge Univ. Press. ISBN 978-1-107-64083-2. OCLC  250050479.
• Ганьшин, В. В. (1969) [1967]. Геометрия земного эллипсоида . Перевод Уиллиса, Дж. М. Сент-Луис: Аэронавигационный картографический и информационный центр. дои : 10.5281/zenodo.32854. ОСЛК  493553.Перевод с русского языка Геометрия земного эллипсоида (Москва, 1967).
• Гаусс, К. Ф. (1902) [1828]. Общие исследования кривых поверхностей 1827 и 1825 годов. Перевод Морхеда, Дж. К.; Хилтебайтеля, А. М. Принстонская ун-та. Lib. OCLC  7824448.PDF. Английский перевод Disquisitiones Generales Circa Superficies Curvas (Дитерих, Геттинген, 1828 г.).
• Харт, А.С. (1849). «Геометрическая демонстрация некоторых свойств геодезических линий». Cambridge and Dublin Mathematical Journal . 4 : 80–84.
• Helmert, FR (1964) [1880]. Математические и физические теории высшей геодезии . Том 1. Сент-Луис: Центр аэронавигационных карт и информации. doi : 10.5281/zenodo.32050. OCLC  17273288.Английский перевод книги Die Mathematischen und Physikalischen Theorieen der Höheren Geodäsie, Vol. 1 (Тойбнер, Лейпциг, 1880 г.).
• Гильберт, Д.; Кон -Фоссен, С. (1952). Геометрия и воображение . Перевод Неменьи, П. Нью-Йорк: Челси. ISBN 9780828400879. OCLC  301610346.
• Хаттон, К. (1811). Курс математики в трех томах, составленный для использования в Королевской военной академии. Том 3. Лондон: FC и J. Rivington. OCLC  18031510.
• Якоби, CGJ (1837). «Zur Theorie der Variations-Rechnung und der Differential-Gleichungen» [Теория вариационного исчисления и дифференциальных уравнений]. Journal für die Reine und Angewandte Mathematik (на немецком языке). 1837 (17): 68–82. дои : 10.1515/crll.1837.17.68. S2CID  119469290.
• Якоби, CGJ (1839). «Note von der geodätischen Linie auf einem Ellipsoid und den verschiedenen Anwendungen einer merkwürdigen analytischen Substitution» [Геодезическая на эллипсоиде и различные применения замечательной аналитической подстановки]. Journal für die Reine und Angewandte Mathematik (на немецком языке). 1839 (19): 309–313. дои : 10.1515/crll.1839.19.309. S2CID  121670851.Письмо Бесселю, 28 декабря 1838 г. Французский перевод (1841 г.).
• Якоби, CGJ (2009) [1866]. А. Клебш (ред.). Лекции по динамике . Перевод Балагангадхарана, К. Нью-Дели: Hindustan Book Agency. ISBN 978-81-85931-91-3. MR  2569315. OCLC  440645889.Английский перевод Vorlesungen über Dynamik (Раймер, Берлин, 1866 г.). Ошибка.
• Якоби, CGJ (1891). «Über die Curve, welche alle von einem Punkte ausgehenden geodätischen Linien eines Rotationsellipsoides berührt» [Огибающая геодезических линий, исходящих из одной точки эллипсоида]. В KTW Weierstrass (ред.). Gesammelte Werke Якоби (на немецком языке). Том. 7. Берлин: Реймер. стр. 72–87. ОСЛК  630416023.Op. post., завершено FHA Wangerin . PDF.
• Джекели, К. (2012), Геометрические системы отсчета в геодезии , Университет штата Огайо, hdl :1811/51274
• Jordan, W. ; Eggert, O. (1962) [1941]. Справочник по геодезии . Том 3. Перевод Carta, MW Washington, DC: Army Map Service. Bibcode : 1962hage.book.....J. doi : 10.5281/zenodo.35316. OCLC  34429043.Английский перевод Handbuch der Vermessungskunde , 8-е издание (Мецлер, Штутгарт, 1941).
• Karney, CFF (2013). «Алгоритмы для геодезических задач». Journal of Geodesy . 87 (1): 43–55. arXiv : 1109.4448 . Bibcode : 2013JGeod..87...43K. doi : 10.1007/s00190-012-0578-z .Дополнения.
• Карни, CFF (2015). "GeographicLib". Версия 1.44.
• Карни, CFF (2024). «Геодезические на произвольном эллипсоиде вращения». Журнал геодезии . 98 (1): 4:1–14. arXiv : 2208.00492 . doi : 10.1007/s00190-023-01813-2 .
• Клингенберг, WPA (1982). Риманова геометрия . де Грюйер. ISBN 978-3-11-008673-7. MR  0666697. OCLC  8476832.
• Кнёррер, Х. (1980). «Геодезика на эллипсоиде». Математические изобретения . 59 (2): 119–143. Бибкод : 1980InMat..59..119K. дои : 10.1007/BF01390041. S2CID  118792545.
• Кракивский, Э. Дж.; Томсон, Д. Б. (1974), Геодезические вычисления положения (PDF) , Кафедра геодезии и геоматики, Конспект лекций, Фредериктон, Нью-Брансуик: Университет Нью-Брансуика, Bibcode : 1974gpc..book.....K
• Лаплас, PS (1829) [1799a]. "Книга 1, §8.". Трактат о небесной механике . Том 1. Перевод Боудича, Н. Бостон: Хиллард, Грей, Литтл и Уилкинс. OCLC  1294937.
• Лаплас, PS (1799b). Traité de Mécanique Céleste [ Трактат о небесной механике ] (на французском языке). Том. 2. Париж: Крепле. п. 112. ОСЛК  25448952.
• Лежандр, AM (1806 г.). «Анализ треугольных трассировок на поверхности сфероида» [Анализ сфероидальных треугольников]. Mémoires de l'Institut National de France (на французском языке) (1-й семестр): 130–161.
• Лежандр, AM (1811). Exercices de Calcul Intégral sur Divers Ordres de Transcendantes et sur les Quadratures [ Упражнения по интегральному исчислению ] (на французском языке). Париж: Курьер. ОСЛК  312469983.
• Лейк, А.; Рапопорт, Л.; Татарников, Д. (2015). Спутниковая съемка GPS (4-е изд.). Уайли. ISBN 978-1-119-01828-5.
• Лиувилл, Дж. (1846 г.). «Sur quelques cas particuliers où les équations du mouvement d'un point matériel peuvent s'intégrer» [Об особых случаях, когда уравнения движения точечной частицы могут быть проинтегрированы]. Journal de Mathématiques Pures et Appliquées (на французском языке). 11 : 345–378.PDF
• Люстерник, Л. (1964). Кратчайшие пути: вариационные задачи . Популярные лекции по математике. Т. 13. Перевод Коллинза, П.; Брауна, Р. Б. Нью-Йорк: Macmillan. MR  0178386. OCLC  1048605.Перевод с русского языка Кратчайшие Линии: Вариационные Задачи (Москва, 1955).
• Монж, Г. (1850) [1796]. «Sur les lignes de Courbure de la Surface de l'ellipsoïde» [О линиях кривизны на поверхности эллипсоида]. В Дж. Лиувилле (ред.). Приложение de l'Analyse à la Géometrie (на французском языке) (5-е изд.). Париж: Башелье. стр. 139–160. ОСЛК  2829112.(Рис. 1–2, Рис. 3–4). Издание 1796 г. (Рис. 1–2, Рис. 3–4). Рисунки в формате PDF.
• Национальная геодезическая служба (2012). «Геодезические утилиты: обратные и прямые». Версия 3.0.
• Ньютон, И. (1848) [1687]. «Книга 3, Предложение 19, Задача 3». Математические начала натуральной философии . Перевод Мотта, А. Нью-Йорк: Adee. С. 405–409.Английский перевод Philosophiæ Naturalis Principia Mathematica . Liber Tertius, положение XIX. Проб. II. стр. 422–424.
• Ориани, Б. (1806). «Элементы сфероидальной тригонометрии». Memorie dell'Istituto Nazionale Italiano (на итальянском языке). 1 (1): 118–198.
• Ориани, Б. (1808). «Элементы сфероидальной тригонометрии». Memorie dell'Istituto Nazionale Italiano (на итальянском языке). 2 (1): 1–58.
• Ориани, Б. (1810). «Элементы сфероидальной тригонометрии». Memorie dell'Istituto Nazionale Italiano (на итальянском языке). 2 (2): 1–58.
• Пуанкаре, Х. (1905). «Sur les lignes géodésiques des Surfaces выпуклых» [Геодезические линии на выпуклых поверхностях]. Труды Американского математического общества (на французском языке). 6 (3): 237–274. дои : 10.2307/1986219. JSTOR  1986219.
• Rainsford, HF (1955). «Длинные геодезические на эллипсоиде». Bulletin Géodésique . 37 (1): 12–22. Bibcode : 1955BGeod..29...12R. doi : 10.1007/BF02527187. S2CID  122111614.
• Рапп, Р. Х. (1991), Геометрическая геодезия, часть I , Университет штата Огайо, hdl :1811/24333
• Рапп, Р. Х. (1993), Геометрическая геодезия, часть II , Университет штата Огайо, hdl :1811/24409
• RNAV (2007). «Приложение 2». Приказ 8260.54A, Стандарт Соединенных Штатов для зональной навигации (PDF) (Технический отчет). Вашингтон, округ Колумбия: Федеральное управление гражданской авиации США.
• Sjöberg, LE (2006). «Определение площадей на плоскости, сфере и эллипсоиде». Обзор . 38 (301): 583–593. doi :10.1179/003962606780732100.
• UNCLOS (2006). Руководство по техническим аспектам Конвенции Организации Объединенных Наций по морскому праву 1982 г. (PDF) (Технический отчет) (4-е изд.). Монако: Международное гидрографическое бюро. Архивировано из оригинала (PDF) 24.05.2013 . Получено 15.08.2013 .
• Vincenty, T. (1975). "Прямые и обратные решения геодезических на эллипсоиде с применением вложенных уравнений" (PDF) . Обзор . 23 (176): 88–93. Bibcode :1975SurRv..23...88V. doi :10.1179/sre.1975.23.176.88. Приложение: Обзор обзора 23 (180): 294 (1976).
• Винсенти, Т.; Боуринг, Б. Р. (1978). Применение трехмерной геодезии к корректировке горизонтальных сетей (PDF) (Технический отчет). NOAA. NOS NGS-13.
• Вейерштрасс, KTW (1861 г.). «Über die geodätischen Linien auf dem dreiaxigen Ellipsoid» [Геодезические линии на трёхосном эллипсоиде]. Monatsberichte der Königlichen Akademie der Wissenschaft zu Berlin (на немецком языке): 986–997.

Внешние ссылки

• Онлайн-библиография книг и статей по геодезии на эллипсоидах.
• Тестовый набор для геодезических линий, набор из 500000 геодезических линий для эллипсоида WGS84, вычисленных с использованием высокоточной арифметики.
• Инструмент NGS, реализующий Vincenty (1975).
• geod(1), страница руководства по утилите PROJ для геодезических расчетов.
• Реализация GeographicLib Карни (2013).
• Построение геодезических линий на Google Maps.