Эйлерова характеристика

Топологический инвариант в математике

В математике , а более конкретно в алгебраической топологии и многогранной комбинаторике , характеристика Эйлера (или число Эйлера , или характеристика Эйлера-Пуанкаре ) является топологическим инвариантом , числом, которое описывает форму или структуру топологического пространства независимо от того, каким образом оно является. согнутый. Его обычно обозначают ( греческой строчной буквой хи ). ${\displaystyle \chi }$

Характеристика Эйлера изначально была определена для многогранников и использовалась для доказательства различных теорем о них, включая классификацию Платоновых тел . Это было указано для Платоновых тел в 1537 году в неопубликованной рукописи Франческо Мауролико . ^[1] Леонард Эйлер , в честь которого названа эта концепция, ввел ее для выпуклых многогранников в более общем смысле, но не смог строго доказать, что она является инвариантом. В современной математике эйлерова характеристика возникает из гомологии и, более абстрактно, гомологической алгебры .

Многогранники

Вершина, ребро и грань куба

Эйлерова характеристика χ классически определялась для поверхностей многогранников по формуле

${\displaystyle \chi =V-E+F}$

где V , E и F — соответственно количество вершин (углов), ребер и граней в данном многограннике . Поверхность любого выпуклого многогранника имеет эйлерову характеристику.

${\displaystyle \ \chi =V-E+F=2~.}$

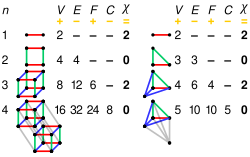
Это уравнение, сформулированное Эйлером в 1758 году, ^[2] известно как формула многогранника Эйлера . ^[3] Это соответствует эйлеровой характеристике сферы ( т.е. ) и одинаково применимо к сферическим многогранникам . Иллюстрация формулы для всех платоновых многогранников приведена ниже. ${\displaystyle \ \chi =2\ }$

Поверхности невыпуклых многогранников могут иметь различные эйлеровы характеристики:

Для правильных многогранников Артур Кэли вывел модифицированную форму формулы Эйлера, используя плотность D , плотность вершин и плотность граней. ${\displaystyle \ d_{v}\ ,}$ ${\displaystyle \ d_{f}\ :}$

${\displaystyle \ d_{v}V-E+d_{f}F=2D~.}$

Эта версия справедлива как для выпуклых многогранников (где все плотности равны 1), так и для невыпуклых многогранников Кеплера – Пуансо .

Все проективные многогранники имеют эйлерову характеристику 1, как и вещественная проективная плоскость , в то время как все поверхности тороидальных многогранников имеют эйлерову характеристику 0, как тор .

Плоские графы

Эйлерова характеристика может быть определена для связных плоских графов по той же формуле, что и для многогранных поверхностей, где F — количество граней в графе, включая внешнюю грань. ${\displaystyle \ V-E+F\ }$

Эйлерова характеристика любого плоского связного графа G равна 2. Это легко доказывается индукцией по количеству граней, определяемых G , начиная с дерева в качестве базового случая. Для деревьев и если G имеет C компонентов (несвязных графов), тот же аргумент индукцией по F показывает, что одна из немногих статей Коши по теории графов также доказывает этот результат. ${\displaystyle \ E=V-1\ }$ ${\displaystyle \ F=1~.}$ ${\displaystyle \ V-E+F-C=1~.}$

Посредством стереографической проекции плоскость отображается в 2-сферу, так что связный граф отображается в многоугольное разложение сферы, имеющей эйлерову характеристику 2. Эта точка зрения неявно проявляется в доказательстве Коши формулы Эйлера, приведенном ниже.

Доказательство формулы Эйлера

Первые шаги доказательства в случае куба

Существует множество доказательств формулы Эйлера. Одно из них было дано Коши в 1811 году следующим образом. Это применимо к любому выпуклому многограннику и, в более общем плане, к любому многограннику, граница которого топологически эквивалентна сфере, а грани топологически эквивалентны дискам.

Удалите одну грань многогранной поверхности. Оттягивая края отсутствующей грани друг от друга, деформируйте все остальные в плоский граф из точек и кривых таким образом, чтобы периметр отсутствующей грани располагался снаружи, окружая полученный граф, как показано на рисунке. первый из трех графиков для частного случая куба. (Предположение о том, что многогранная поверхность вначале гомеоморфна сфере, делает это возможным.) После этой деформации правильные грани, как правило, перестают быть правильными. Число вершин и ребер осталось прежним, а количество граней уменьшено на 1. Поэтому доказательство формулы Эйлера для многогранника сводится к доказательству для этого деформированного плоского объекта. ${\displaystyle \ V-E+F=1\ }$

Если есть грань с более чем тремя сторонами, нарисуйте диагональ, то есть кривую, проходящую через грань, соединяющую две вершины, которые еще не соединены. Каждая новая диагональ добавляет одно ребро и одну грань и не меняет количество вершин, поэтому она не меняет количества (Здесь необходимо предположение, что все грани являются дисками, чтобы показать с помощью теоремы Жордана о кривой , что эта операция увеличивает число граней на одну.) Продолжайте добавлять ребра таким образом, пока все грани не станут треугольными. ${\displaystyle \ V-E+F~.}$

Повторно примените любое из следующих двух преобразований, сохраняя инвариант, согласно которому внешняя граница всегда является простым циклом :

1. Удалите треугольник, у которого только одна грань примыкает к внешней стороне, как показано на втором графике. Это уменьшает количество ребер и граней на одну каждую и не меняет количество вершин, поэтому сохраняет ${\displaystyle \ V-E+F~.}$
2. Удалите треугольник с двумя ребрами, общими для внешней части сети, как показано на третьем графике. При каждом удалении треугольника удаляется вершина, два ребра и одна грань, поэтому сохраняется ${\displaystyle \ V-E+F~.}$

Эти преобразования в конечном итоге сводят плоский граф к одному треугольнику. (Без инварианта простого цикла удаление треугольника может привести к отключению остальных треугольников, что сделает недействительной остальную часть аргумента. Правильный порядок удаления является элементарным примером обстрела . )

В этот момент одинокий треугольник имеет и так, что Поскольку каждый из двух вышеуказанных шагов преобразования сохранил эту величину, мы показали это для деформированного плоского объекта, что демонстрируется, таким образом, для многогранника. Это доказывает теорему. ${\displaystyle \ V=3\ ,}$ ${\displaystyle \ E=3\ ,}$ ${\displaystyle \ F=1\ ,}$ ${\displaystyle \ V-E+F=1~.}$ ${\displaystyle \ V-E+F=1\ }$ ${\displaystyle \ V-E+F=2\ }$

Дополнительные доказательства см. в Eppstein (2013). ^[4] Множественные доказательства, включая их недостатки и ограничения, используются в качестве примеров в книге Лакатоса «Доказательства и опровержения» (1976). ^[5]

Топологическое определение

Обсуждаемые выше полиэдральные поверхности представляют собой, выражаясь современным языком, двумерные конечные CW-комплексы . (Когда используются только треугольные грани, они представляют собой двумерные конечные симплициальные комплексы .) В общем, для любого конечного CW-комплекса эйлерову характеристику можно определить как знакопеременную сумму

${\displaystyle \chi =k_{0}-k_{1}+k_{2}-k_{3}+\cdots ,}$

где k _n обозначает количество ячеек размерности n в комплексе.

Аналогично, для симплициального комплекса эйлерова характеристика равна знакопеременной сумме

${\displaystyle \chi =k_{0}-k_{1}+k_{2}-k_{3}+\cdots ,}$

где k _n обозначает количество n -симплексов в комплексе.

Альтернативный номер Бетти

В более общем смысле для любого топологического пространства мы можем определить n- е число Бетти b _n как ранг n -й сингулярной группы гомологии . Тогда эйлерову характеристику можно определить как знакопеременную сумму

${\displaystyle \chi =b_{0}-b_{1}+b_{2}-b_{3}+\cdots .}$

Эта величина корректно определена, если все числа Бетти конечны и если они равны нулю после определенного индекса  n ₀ . Для симплициальных комплексов это не то же определение, что в предыдущем абзаце, но вычисление гомологии показывает, что два определения дадут одно и то же значение для . ${\displaystyle \chi }$

Характеристики

Эйлерова характеристика хорошо ведет себя по отношению ко многим основным операциям над топологическими пространствами следующим образом.

Гомотопическая инвариантность

Гомология является топологическим инвариантом и, более того, гомотопическим инвариантом : два топологических пространства, которые гомотопически эквивалентны, имеют изоморфные группы гомологий. Отсюда следует, что эйлерова характеристика также является гомотопическим инвариантом.

Например, любое стягиваемое пространство (то есть одна гомотопия, эквивалентная точке) имеет тривиальную гомологию, а это означает, что 0-е число Бетти равно 1, а остальные 0. Следовательно, его эйлерова характеристика равна 1. Этот случай включает евклидово пространство любой размерности. , а также твердый единичный шар в любом евклидовом пространстве — одномерный интервал, двумерный диск, трехмерный шар и т. д. ${\displaystyle \mathbb {R} ^{n}}$

Другой пример: любой выпуклый многогранник гомеоморфен трехмерному шару , поэтому его поверхность гомеоморфна (следовательно, гомотопически эквивалентна) двумерной сфере , имеющей эйлерову характеристику 2. Это объясняет, почему выпуклые многогранники имеют эйлерову характеристику 2.

Принцип включения-исключения

Если M и N — любые два топологических пространства, то эйлерова характеристика их непересекающегося объединения является суммой их эйлеровых характеристик, поскольку гомологии аддитивны при непересекающемся объединении:

${\displaystyle \chi (M\sqcup N)=\chi (M)+\chi (N).}$

В более общем смысле, если M и N являются подпространствами большего пространства X , то такими же являются и их объединение и пересечение. В некоторых случаях характеристика Эйлера подчиняется версии принципа включения-исключения :

${\displaystyle \chi (M\cup N)=\chi (M)+\chi (N)-\chi (M\cap N).}$

Это справедливо в следующих случаях:

• если M и N — эксцизная пара. В частности, если внутренности M и N внутри объединения все еще покрывают объединение. ^[6]
• если X — локально компактное пространство и используются эйлеровы характеристики с компактными носителями , никаких предположений относительно M или N не требуется.
• если X — стратифицированное пространство, все страты которого четномерны, принцип включения-исключения справедлив, если M и N — объединения стратов. Это применимо, в частности, если M и N — подмногообразия комплексного алгебраического многообразия . ^[7]

В целом принцип включения-исключения неверен. В качестве контрпримера можно взять X за действительную прямую , M за подмножество , состоящее из одной точки, а N за дополнение к M.

Связная сумма

Для двух связных замкнутых n-многообразий можно получить новое связное многообразие с помощью операции связной суммы . Эйлерова характеристика связана формулой ^[8] ${\displaystyle M,N}$ ${\displaystyle M\#N}$

${\displaystyle \chi (M\#N)=\chi (M)+\chi (N)-\chi (S^{n}).}$

Свойство продукта

Кроме того, эйлерова характеристика любого пространства произведений M × N равна

${\displaystyle \chi (M\times N)=\chi (M)\cdot \chi (N).}$

Этими свойствами сложения и умножения обладает также мощность множеств . Таким образом, характеристику Эйлера можно рассматривать как обобщение мощности; см. [1].

Покрытие помещений

Аналогично, для k -листного накрывающего пространства имеем ${\displaystyle {\tilde {M}}\to M,}$

${\displaystyle \chi ({\tilde {M}})=k\cdot \chi (M).}$

В более общем смысле, для разветвленного накрывающего пространства эйлерова характеристика накрытия может быть вычислена из вышесказанного с поправочным коэффициентом для точек ветвления, что дает формулу Римана-Гурвица .

Свойство расслоения

Свойство произведения справедливо в гораздо более общем смысле для расслоений с определенными условиями.

Если - расслоение со слоем F, с базой B линейно связным и расслоение ориентируемо над полем K, то эйлерова характеристика с коэффициентами в поле K удовлетворяет свойству произведения: ^[9] ${\displaystyle p\colon E\to B}$

${\displaystyle \chi (E)=\chi (F)\cdot \chi (B).}$

Сюда входят пространства произведений и пространства накрытия как частные случаи, и это может быть доказано с помощью спектральной последовательности Серра на гомологиях расслоения.

Для расслоений это также можно понимать в терминах трансферного отображения (обратите внимание, что это подъем и оно идет «не в ту сторону»), композиция которого с проекционным отображением представляет собой умножение на класс Эйлера слоя: ^[10] ${\displaystyle \tau \colon H_{*}(B)\to H_{*}(E)}$ ${\displaystyle p_{*}\colon H_{*}(E)\to H_{*}(B)}$

${\displaystyle p_{*}\circ \tau =\chi (F)\cdot 1.}$

Примеры

Поверхности

Эйлерову характеристику можно легко вычислить для общих поверхностей, найдя полигонизацию поверхности (то есть описание как CW-комплекс ) и используя приведенные выше определения.

Футбольный мяч

Футбольные мячи обычно изготавливают путем сшивания пятиугольных и шестиугольных частей, при этом по три части встречаются в каждой вершине (см., например, Adidas Telstar ). Если используются пятиугольники P и шестиугольники H , то есть  грани,  вершины и  ребра. Таким образом, эйлерова характеристика ${\displaystyle \ F=P+H\ }$ ${\displaystyle \ V={\tfrac {1}{3}}\left(\ 5P+6H\ \right)\ }$ ${\displaystyle \ E={\tfrac {1}{2}}\left(\ 5P+6H\ \right)\ }$

${\displaystyle V-E+F={\tfrac {1}{3}}\left(\ 5P+6H\ \right)-{\tfrac {1}{2}}\left(\ 5P+6H\ \right)+P+H={\tfrac {1}{6}}P~.}$

Поскольку сфера имеет эйлерову характеристику 2, отсюда следует, что футбольный мяч, построенный таким образом, всегда имеет 12 пятиугольников. Число шестиугольников может быть любым неотрицательным целым числом, кроме 1. ^[11] Этот результат применим к фуллеренам и многогранникам Гольдберга . ${\displaystyle \ P=12~.}$

Произвольные размеры

Сравнение эйлеровых характеристик гиперкубов и симплексов размерностей от 1 до 4.

k -  мерная сфера имеет особые группы гомологии, равные

${\displaystyle H_{k}(\mathrm {S} ^{n})={\begin{cases}\mathbb {Z} ~&k=0~~{\mathsf {or}}~~k=n\\\{0\}&{\mathsf {otherwise}}\ ,\end{cases}}}$

следовательно, имеет число Бетти 1 в размерностях 0 и n , а все остальные числа Бетти равны 0. Тогда его эйлерова характеристика равна χ = 1 + (−1) ⁿ  ; то есть либо 0, если n нечетное , либо 2, если n четное .

n -  мерное реальное проективное пространство представляет собой фактор n-  сферы по антиподальному отображению . Отсюда следует, что его эйлерова характеристика ровно вдвое меньше, чем у соответствующей сферы – либо 0, либо 1.

n -  мерный тор — это произведение n  кругов. Его эйлерова характеристика равна 0 по свойству произведения. В более общем смысле любое компактное параллелизуемое многообразие , включая любую компактную группу Ли , имеет эйлерову характеристику 0. ^[12]

Эйлерова характеристика любого замкнутого нечетномерного многообразия также равна 0. ^[13] Случай ориентируемых примеров является следствием двойственности Пуанкаре . Это свойство в более общем смысле применимо к любому компактному стратифицированному пространству , все слои которого имеют нечетную размерность. Это также применимо к замкнутым нечетномерным неориентируемым многообразиям через ориентируемое двойное накрытие « два к одному» .

Отношения с другими инвариантами

Эйлерова характеристика замкнутой ориентируемой поверхности может быть вычислена по ее роду g (количество торов в разложении поверхности на связную сумму ; интуитивно - количество «ручек») как

${\displaystyle \chi =2-2g~.}$

Эйлерова характеристика замкнутой неориентируемой поверхности может быть вычислена по ее неориентируемому роду k (числу вещественных проективных плоскостей в разложении поверхности на связную сумму) как

${\displaystyle \chi =2-k~.}$

Для замкнутых гладких многообразий эйлерова характеристика совпадает с числом Эйлера , т. е. классом Эйлера его касательного расслоения , вычисленным на фундаментальном классе многообразия. Класс Эйлера, в свою очередь, относится ко всем другим характеристическим классам векторных расслоений .

Для замкнутых римановых многообразий эйлерову характеристику также можно найти путем интегрирования кривизны; см. теорему Гаусса–Бонне для двумерного случая и обобщенную теорему Гаусса–Бонне для общего случая.

Дискретным аналогом теоремы Гаусса-Бонне является теорема Декарта о том , что «общий дефект » многогранника , измеренный в полных окружностях, является эйлеровой характеристикой многогранника.

Теорема Хадвигера характеризует характеристику Эйлера как уникальную ( с точностью до скалярного умножения ) трансляционно-инвариантную, конечно-аддитивную, не обязательно неотрицательную функцию множества, определенную на конечных объединениях компактных выпуклых множеств в ℝ ⁿ , которая является «однородной степени 0».

Обобщения

Для каждого комбинаторного клеточного комплекса эйлерова характеристика определяется как количество 0-клеток минус количество 1-клеток плюс количество 2-клеток и т. д., если эта знакопеременная сумма конечна. В частности, эйлерова характеристика конечного множества — это просто его мощность, а эйлерова характеристика графа — это количество вершин минус количество ребер. (Олаф Пост называет это «хорошо известной формулой». ^[14] ) .

В более общем смысле можно определить эйлерову характеристику любого цепного комплекса как знакопеременную сумму рангов групп гомологий цепного комплекса, предполагая, что все эти ранги конечны. ^[15]

Вариант эйлеровой характеристики, используемый в алгебраической геометрии , следующий. Для любого когерентного пучка на правильной схеме X его эйлерову характеристику определяют как ${\displaystyle {\mathcal {F}}}$

${\displaystyle \chi ({\mathcal {F}})=\sum _{i}(-1)^{i}h^{i}(X,{\mathcal {F}})\ ,}$

где - размерность i -й группы когомологий пучка . В этом случае все размеры конечны по теореме Гротендика о конечности . Это пример эйлеровой характеристики цепного комплекса, где цепной комплекс представляет собой конечное разрешение ациклических пучков. ${\displaystyle \ h^{i}(X,{\mathcal {F}})\ }$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle \ {\mathcal {F}}\ }$

Другое обобщение понятия эйлеровой характеристики на многообразиях происходит от орбифолдов (см. Эйлерову характеристику орбифолда ). Хотя каждое многообразие имеет целочисленную эйлерову характеристику, орбифолд может иметь дробную эйлерову характеристику. Например, каплевидный орбифолд имеет эйлерову характеристику 1 +1/ п , где p — простое число, соответствующее углу конуса 2 π / п .

Понятие эйлеровой характеристики приведенных гомологий ограниченного конечного ЧУМ является еще одним обобщением, важным в комбинаторике . ЧУ-множество является «ограниченным», если оно имеет наименьший и наибольший элементы; назовем их 0 и 1. Эйлерова характеристика такого ЧУ-множества определяется как целое число ц (0,1) , где ц — функция Мёбиуса в алгебре инцидентности этого ЧУ-множества .

Это можно дополнительно обобщить, определив рациональнозначную эйлерову характеристику для некоторых конечных категорий - понятие, совместимое с эйлеровыми характеристиками графов, орбифолдов и частично упорядоченных множеств, упомянутых выше. В этом случае эйлерова характеристика конечной группы или моноида G равна1/ | г |  , а эйлерова характеристика конечного группоида есть сумма1/ | г _я  |, где мы выбрали одну репрезентативную группу G _i для каждого компонента связности группоида. ^[16]

Смотрите также

• исчисление Эйлера
• класс Эйлера
• Список тем, названных в честь Леонарда Эйлера
• Список однородных многогранников

Рекомендации

Примечания

1. Фридман, Майкл (2018). История складывания в математике: математизация полей . Научные сети. Исторические исследования. Том. 59. Биркхойзер. п. 71. дои : 10.1007/978-3-319-72487-4. ISBN 978-3-319-72486-7.
2. Эйлер, Л. (1758). «Elementa doctrinae Solidorum». Novi Commentarii Academiae Scientiarum Petropolitanae (на латыни): 109–140 – через U. Pacific , Стоктон, Калифорния.
3. Ричесон (2008)
4. Эппштейн, Дэвид (2013). «Двадцать одно доказательство формулы Эйлера: V − E + F = 2» (академ. чел. чбс.) . Проверено 27 мая 2022 г. - через Калифорнийский университет в Ирвине .
5. Лакатос, И. (1976). Доказательства и опровержения . Кембриджская технологическая пресса.
6. Эдвин Спэньер: Алгебраическая топология, Springer 1966, стр. 205.
7. Уильям Фултон: Введение в торические многообразия, 1993, Princeton University Press, стр. 141.
8. "Гомологии связной суммы" . Проверено 13 июля 2016 г.
9. Спэньер, Эдвин Генри (1982), Алгебраическая топология, Springer, ISBN 978-0-387-94426-5, Применение спектральной последовательности гомологии, с. 481
10. Готлиб, Дэниел Генри (1975), «Пучки волокон и характеристика Эйлера» (PDF) , Журнал дифференциальной геометрии , 10 (1): 39–48, doi : 10.4310/jdg/1214432674, S2CID  118905134
11. Фаулер, П.В. и Манолопулос, DE (1995). Атлас фуллеренов . п. 32.
12. Милнор, Дж. В. и Сташефф, Джеймс Д. (1974). Характеристические классы . Издательство Принстонского университета.
13. Ричесон (2008), с. 261
14. Пост, Олаф (2009). «Спектральный анализ метрических графов и связанных с ними пространств». Пределы графов в теории групп и информатике . Лозанна, Швейцария: EPFL Press . стр. 109–140. arXiv : 0712.1507 . Бибкод : 2007arXiv0712.1507P.
15. Эйлерова характеристика в n Lab
16. Ленстер, Том (2008). «Эйлерова характеристика категории» (PDF) . Документа Математика . 13 : 21–49. дои : 10.4171/дм/240. S2CID  1046313. Архивировано из оригинала (PDF) 6 июня 2014 г. - через Университет Иллинойса, Урбана-Шампейн .

Библиография

• Ричесон, DS (2008). Жемчужина Эйлера: формула многогранника и рождение топологии . Издательство Принстонского университета.

дальнейшее чтение

• Флегг, Х. Грэм; От геометрии к топологии , Дувр, 2001, с. 40.

Внешние ссылки

• Вайсштейн, Эрик В. «Эйлерова характеристика». Математический мир .
• Вайсштейн, Эрик В. «Формула многогранника». Математический мир .
• Матвеев, С.В. (2001) [1994], «Эйлерова характеристика», Математическая энциклопедия , EMS Press
• Анимированная версия доказательства формулы Эйлера с использованием сферической геометрии.