Целочисленное разбиение

Разложение целого числа на сумму положительных целых чисел

Диаграммы Юнга, связанные с разбиениями положительных целых чисел от 1 до 8. Они расположены таким образом, что изображения при отражении относительно главной диагонали квадрата являются сопряженными разбиениями.

Разбиения n с наибольшей частью k

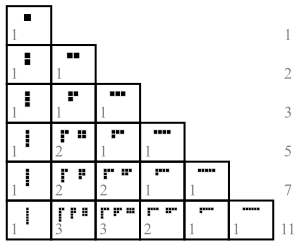
В теории чисел и комбинаторике разбиение неотрицательного целого числа n , также называемое целочисленным разбиением , представляет собой способ записи n в виде суммы положительных целых чисел . Две суммы, отличающиеся только порядком слагаемых, считаются одним и тем же разбиением. (Если порядок имеет значение, сумма становится композицией . ) Например, 4 можно разбить пятью различными способами:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

Единственное разбиение нуля — это пустая сумма, не имеющая частей.

Зависящая от порядка композиция 1 + 3 представляет собой то же самое разбиение, что и 3 + 1 , а две различные композиции 1 + 2 + 1 и 1 + 1 + 2 представляют собой то же самое разбиение, что и 2 + 1 + 1 .

Отдельное слагаемое в разбиении называется частью . Количество разбиений n задается функцией разбиения p ( n ) . Таким образом, p (4) = 5. Обозначение λ ⊢ n означает, что λ является разбиением n .

Разбиения можно графически визуализировать с помощью диаграмм Юнга или диаграмм Феррерса . Они встречаются в ряде разделов математики и физики , включая изучение симметрических многочленов и симметрической группы , а также в теории представления групп в целом.

Примеры

Семь разделов по 5 являются

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

Некоторые авторы рассматривают раздел как убывающую последовательность слагаемых, а не выражение со знаками плюс. Например, раздел 2 + 2 + 1 можно было бы записать как кортеж ( 2, 2, 1) или в еще более компактной форме (2 ² , 1) , где верхний индекс указывает количество повторений части.

Эту нотацию кратности для разбиения можно записать альтернативно как , где m ₁ — количество единиц, m ₂ — количество двоек и т. д. (Компоненты с m _i = 0 могут быть опущены.) Например, в этой нотации разбиения числа 5 записываются как , и . ${\displaystyle 1^{m_{1}}2^{m_{2}}3^{m_{3}}\cdots }$ ${\displaystyle 5^{1},1^{1}4^{1},2^{1}3^{1},1^{2}3^{1},1^{1}2^{2},1^{3}2^{1}}$ ${\displaystyle 1^{5}}$

Схематические изображения разделов

Существует два распространенных метода диаграммного представления разделов: как диаграммы Феррерса, названные в честь Нормана Маклеода Феррерса , и как диаграммы Юнга, названные в честь Альфреда Янга . Оба имеют несколько возможных соглашений; здесь мы используем английскую нотацию , с диаграммами, выровненными в верхнем левом углу.

Диаграмма Феррерса

Разложение 6 + 4 + 3 + 1 числа 14 можно представить следующей диаграммой:

14 кругов выстроены в 4 ряда, каждый из которых имеет размер части разбиения. Диаграммы для 5 разбиений числа 4 показаны ниже:

Диаграмма Юнга

Альтернативным визуальным представлением целочисленного разбиения является его диаграмма Юнга (часто также называемая диаграммой Феррерса). Вместо представления разбиения точками, как на диаграмме Феррерса, диаграмма Юнга использует коробки или квадраты. Таким образом, диаграмма Юнга для разбиения 5 + 4 + 1 выглядит следующим образом:

в то время как диаграмма Феррерса для того же раздела

Хотя эта, казалось бы, тривиальная вариация не кажется достойной отдельного упоминания, диаграммы Юнга оказываются чрезвычайно полезными при изучении симметричных функций и теории представления групп : заполнение ячеек диаграмм Юнга числами (или иногда более сложными объектами), подчиняющимися различным правилам, приводит к семейству объектов, называемых таблицами Юнга , и эти таблицы имеют комбинаторное и теоретико-представительное значение. ^[1] Как тип фигуры, образованной смежными квадратами, соединенными вместе, диаграммы Юнга являются особым видом полимино . ^[2]

Функция разделения

Использование метода Эйлера для нахождения p (40): Линейка со знаками плюс и минус (серый ящик) сдвигается вниз, соответствующие части добавляются или вычитаются. Положения знаков задаются разностями чередующихся натуральных (синий) и нечетных (оранжевый) чисел. В файле SVG наведите курсор на изображение, чтобы переместить линейку.

Функция разбиения подсчитывает разбиения неотрицательного целого числа . Например, поскольку целое число имеет пять разбиений , , , , и . Значения этой функции для следующие: ${\displaystyle p(n)}$ ${\displaystyle n}$ ${\displaystyle p(4)=5}$ ${\displaystyle 4}$ ${\displaystyle 1+1+1+1}$ ${\displaystyle 1+1+2}$ ${\displaystyle 1+3}$ ${\displaystyle 2+2}$ ${\displaystyle 4}$ ${\displaystyle n=0,1,2,\dots }$

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (последовательность A000041 в OEIS ).

Производящая функция равна​ ${\displaystyle p}$

${\displaystyle \sum _{n=0}^{\infty }p(n)q^{n}=\prod _{j=1}^{\infty }\sum _{i=0}^{\infty }q^{ji}=\prod _{j=1}^{\infty }(1-q^{j})^{-1}.}$

Неизвестно ни одного замкнутого выражения для функции распределения, но у нее есть как асимптотические разложения , которые точно ее приближают, так и рекуррентные соотношения, с помощью которых ее можно точно вычислить. Она растет как экспоненциальная функция квадратного корня ее аргумента., ^[3] следующим образом:

${\displaystyle p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \left({\pi {\sqrt {\frac {2n}{3}}}}\right)}$как ${\displaystyle n\to \infty }$

В 1937 году Ганс Радемахер нашел способ представления статистической суммы сходящимся рядом ${\displaystyle p(n)}$

$${\displaystyle p(n)={\frac {1}{\pi {\sqrt {2}}}}\sum _{k=1}^{\infty }A_{k}(n){\sqrt {k}}\cdot {\frac {d}{dn}}\left({{\frac {1}{\sqrt {n-{\frac {1}{24}}}}}\sinh \left[{{\frac {\pi }{k}}{\sqrt {{\frac {2}{3}}\left(n-{\frac {1}{24}}\right)}}}\,\,\,\right]}\right)}$$где

$${\displaystyle A_{k}(n)=\sum _{0\leq m<k,\;(m,k)=1}e^{\pi i\left(s(m,k)-2nm/k\right)}.}$$и является суммой Дедекинда . ${\displaystyle s(m,k)}$

Мультипликативной обратной функцией ее производящей функции является функция Эйлера ; по теореме Эйлера о пятиугольных числах эта функция является знакопеременной суммой степеней пятиугольных чисел своего аргумента.

${\displaystyle p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+\cdots }$

Шриниваса Рамануджан обнаружил, что функция разбиения имеет нетривиальные закономерности в модульной арифметике , теперь известные как сравнения Рамануджана . Например, всякий раз, когда десятичное представление заканчивается цифрой 4 или 9, число разбиений будет делиться на 5. ^[4] ${\displaystyle n}$ ${\displaystyle n}$

Ограниченные разделы

Как в комбинаторике, так и в теории чисел часто изучаются семейства разбиений, подверженные различным ограничениям. ^[5] В этом разделе рассматривается несколько таких ограничений.

Сопряженные и самосопряженные разбиения

Если перевернуть диаграмму разбиения 6 + 4 + 3 + 1 вдоль ее главной диагонали, то получим еще одно разбиение 14:

Превращая строки в столбцы, получаем разбиение 4 + 3 + 3 + 2 + 1 + 1 числа 14. Такие разбиения называются сопряженными друг другу. ^[6] В случае числа 4 разбиения 4 и 1 + 1 + 1 + 1 являются сопряженными парами, а разбиения 3 + 1 и 2 + 1 + 1 сопряжены друг другу. Особый интерес представляют разбиения, такие как 2 + 2, которые сами являются сопряженными. Такие разбиения называются самосопряженными . [ ^7]

Утверждение : Число самосопряженных разбиений равно числу разбиений с различными нечетными частями.

Доказательство (схема) : Главное наблюдение состоит в том, что каждую нечетную часть можно « сложить » в середине, образовав самосопряженную диаграмму:

Затем можно получить биекцию между множеством разбиений с различными нечетными частями и множеством самосопряженных разбиений, как показано в следующем примере:

Нечетные части и отдельные части

Среди 22 разбиений числа 8 есть 6, которые содержат только нечетные части :

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

В качестве альтернативы мы могли бы посчитать разделы, в которых ни одно число не встречается более одного раза. Такой раздел называется разделом с различными частями . Если мы посчитаем разделы 8 с различными частями, мы также получим 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Это общее свойство. Для каждого положительного числа число разбиений с нечетными частями равно числу разбиений с различными частями, обозначаемому как q ( n ). ^{[8] [9]} Этот результат был доказан Леонардом Эйлером в 1748 году ^[10] и позднее был обобщен как теорема Глейшера .

Для каждого типа ограниченного разбиения существует соответствующая функция для количества разбиений, удовлетворяющих данному ограничению. Важным примером является q ( n ) (разбиения на отдельные части). Первые несколько значений q ( n ) (начиная с q (0)=1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (последовательность A000009 в OEIS ).

Производящая функция для q ( n ) определяется выражением ^[11]

${\displaystyle \sum _{n=0}^{\infty }q(n)x^{n}=\prod _{k=1}^{\infty }(1+x^{k})=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.}$

Теорема о пятиугольных числах дает рекуррентное соотношение для q : ^[12]

q ( ​​k ) = ak + _q ( k − 1) + q ( k − 2) − q ( k − 5) − q ( k − 7) + q ( k − 12) + q ( k − 15) − q ( k − 22) − ...

где a _k равно (−1) ^m , если k = 3 m ² − m для некоторого целого числа m, и равно 0 в противном случае.

Ограниченный размер детали или количество деталей

Принимая сопряженные значения, число p _k ( n ) разбиений n на ровно k частей равно числу разбиений n , в которых наибольшая часть имеет размер k . Функция p _k ( n ) удовлетворяет рекуррентному соотношению

п _к ( п ) = п _к ( п − к ) + п _{к −1} ( п − 1)

с начальными значениями p ₀ (0) = 1 и p _k ( n ) = 0, если n ≤ 0 или k ≤ 0 и n и k не оба равны нулю. ^[13]

Функцию p ( n ) можно восстановить с помощью

${\displaystyle p(n)=\sum _{k=0}^{n}p_{k}(n).}$

Одной из возможных функций-производителей для таких разбиений, принимающих k фиксированным и n переменным, является

${\displaystyle \sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\prod _{i=1}^{k}{\frac {1}{1-x^{i}}}.}$

В более общем случае, если T — множество положительных целых чисел, то число разбиений n , все части которых принадлежат T , имеет производящую функцию

${\displaystyle \prod _{t\in T}(1-x^{t})^{-1}.}$

Это можно использовать для решения задач по размену (где множество T определяет доступные монеты). В качестве двух частных случаев, один из них имеет, что количество разделов n , в которых все части равны 1 или 2 (или, что эквивалентно, количество разделов n на 1 или 2 части) равно

${\displaystyle \left\lfloor {\frac {n}{2}}+1\right\rfloor ,}$

а число разбиений n, в которых все части равны 1, 2 или 3 (или, что эквивалентно, число разбиений n на не более чем три части) является ближайшим целым числом к ​​( n + 3) ² / 12. ^[14]

Разбиения в прямоугольнике и гауссовские биномиальные коэффициенты

Можно также одновременно ограничить количество и размер частей. Пусть p ( N , M ; n ) обозначает количество разбиений n с не более чем M частями, каждое размером не более N . Эквивалентно, это разбиения, диаграмма Юнга которых помещается внутри прямоугольника M × N. Существует рекуррентное соотношение, полученное путем наблюдения, которое подсчитывает разбиения n на ровно M частей размером не более N , и вычитание 1 из каждой части такого разбиения дает разбиение n − M не более чем на M частей. ^[15] $${\displaystyle p(N,M;n)=p(N,M-1;n)+p(N-1,M;n-M)}$$ ${\displaystyle p(N,M;n)-p(N,M-1;n)}$

Гауссовский биномиальный коэффициент определяется как: Гауссовский биномиальный коэффициент связан с производящей функцией p ( N , M ; n ) равенством $${\displaystyle {k+\ell \choose \ell }_{q}={k+\ell \choose k}_{q}={\frac {\prod _{j=1}^{k+\ell }(1-q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j})}}.}$$ $${\displaystyle \sum _{n=0}^{MN}p(N,M;n)q^{n}={M+N \choose M}_{q}.}$$

Площадь Ранка и Дёрфи

Ранг разбиения — это наибольшее число k , такое, что разбиение содержит не менее k частей размером не менее k . Например, разбиение 4 + 3 + 3 + 2 + 1 + 1 имеет ранг 3, поскольку оно содержит 3 части, которые ≥ 3, но не содержит 4 частей, которые ≥ 4. В диаграмме Феррерса или диаграмме Юнга разбиения ранга r квадрат r × r записей в верхнем левом углу известен как квадрат Дёрфи :

Квадрат Дёрфи применяется в комбинаторике при доказательстве различных тождеств разбиения. ^[16] Он также имеет некоторое практическое значение в форме индекса Хирша .

Другая статистика также иногда называется рангом разбиения (или рангом Дайсона), а именно разницей для разбиения из k частей с наибольшей частью . Эта статистика (которая не связана с той, что описана выше) появляется в исследовании сравнений Рамануджана . ${\displaystyle \lambda _{k}-k}$ ${\displaystyle \lambda _{k}}$

решетка Юнга

Существует естественный частичный порядок на разбиениях, заданный включением диаграмм Юнга. Этот частично упорядоченный набор известен как решетка Юнга . Решетка была первоначально определена в контексте теории представлений , где она использовалась для описания неприводимых представлений симметрических групп S _n для всех n , вместе с их свойствами ветвления, в характеристике ноль. Она также получила значительное изучение своих чисто комбинаторных свойств; в частности, она является мотивирующим примером дифференциального частично упорядоченного множества .

Случайные разделы

Существует глубокая теория случайных разбиений, выбранных в соответствии с равномерным распределением вероятностей на симметрической группе через соответствие Робинсона–Шенстеда . В 1977 году Логан и Шепп, а также Вершик и Керов показали, что диаграмма Юнга типичного большого разбиения становится асимптотически близкой к графику некоторой аналитической функции, минимизирующей определенный функционал. В 1988 году Байк, Дейфт и Йоханссон расширили эти результаты, чтобы определить распределение самой длинной возрастающей подпоследовательности случайной перестановки в терминах распределения Трейси–Уидома . ^[17] Окуньков связал эти результаты с комбинаторикой римановых поверхностей и теорией представлений. ^{[18] [19]}

Смотрите также

• Ранг раздела , другое понятие ранга
• Рукоятка перегородки
• Порядок доминирования
• Факторизация
• Факторизация целых чисел
• Разделение множества
• Звезды и полосы (комбинаторика)
• Плоская перегородка
• Вежливое число , определяемое путем разбиения на последовательные целые числа
• Мультипликативное разбиение
• Двенадцатикратный путь
• Формула выборки Эвенса
• Формула Фаа ди Бруно
• Многораздельный
• Тождества Ньютона
• Функция наименьших частей
• Разбиение Гольдбаха — это разбиение четного числа на простые числа (см. гипотезу Гольдбаха ).
• Функция распределения Костанта

Примечания

1. Эндрюс 1976, стр. 199.
2. Josuat-Vergès, Matthieu (2010), «Биекции между избегающими шаблонов заполнениями диаграмм Юнга», Журнал комбинаторной теории , Серия A, 117 (8): 1218–1230, arXiv : 0801.4928 , doi : 10.1016/j.jcta.2010.03.006, MR  2677686, S2CID  15392503.
3. Эндрюс 1976, стр. 69.
4. Харди и Райт 2008, стр. 380.
5. Олдер, Генри Л. (1969). «Тождества разбиения — от Эйлера до наших дней». American Mathematical Monthly . 76 (7): 733–746. doi :10.2307/2317861. JSTOR  2317861.
6. Харди и Райт 2008, стр. 362.
7. Харди и Райт 2008, стр. 368.
8. Харди и Райт 2008, стр. 365.
9. Обозначения соответствуют Abramowitz & Stegun 1964, стр. 825.
10. Эндрюс, Джордж Э. (1971). Теория чисел . Филадельфия: WB Saunders Company. С. 149–50.
11. Абрамовиц и Стеган 1964, стр. 825, 24.2.2 уравнение I(B)
12. Абрамовиц и Стеган 1964, стр. 826, 24.2.2 уравнение II(A)
13. Ричард Стэнли, Перечислительная комбинаторика , том 1, второе издание. Cambridge University Press, 2012. Глава 1, раздел 1.7.
14. Харди, Г. Х. (1920). Некоторые известные проблемы теории чисел. Clarendon Press.
15. Эндрюс 1976, стр. 33–34.
16. см., например, Стэнли 1999, стр. 58
17. Ромик, Дэн (2015). Удивительная математика длиннейших возрастающих подпоследовательностей . Учебники Института математической статистики. Нью-Йорк: Cambridge University Press. ISBN 978-1-107-42882-9.
18. Окуньков, Андрей (2000). «Случайные матрицы и случайные перестановки». International Mathematics Research Notices . 2000 (20): 1043. doi : 10.1155/S1073792800000532 . S2CID  14308256.
19. Окуньков, А. (2001-04-01). «Бесконечный клин и случайные разбиения». Selecta Mathematica . 7 (1): 57–81. arXiv : math/9907127 . doi :10.1007/PL00001398. ISSN  1420-9020. S2CID  119176413.

Ссылки

• Абрамовиц, Милтон ; Стиган, Ирен (1964). Справочник по математическим функциям с формулами, графиками и математическими таблицами . Министерство торговли США, Национальное бюро стандартов. ISBN 0-486-61272-4.
• Эндрюс, Джордж Э. (1976). Теория разделов . Cambridge University Press. ISBN 0-521-63766-X.
• Эндрюс, Джордж Э.; Эрикссон, Киммо (2004). Целочисленные разбиения . Cambridge University Press. ISBN 0-521-60090-1.
• Апостол, Том М. (1990) [1976]. Модулярные функции и ряды Дирихле в теории чисел . Graduate Texts in Mathematics . Vol. 41 (2nd ed.). New York etc.: Springer-Verlag . ISBN 0-387-97127-0. Збл  0697.10023. (См. главу 5 для современного педагогического введения в формулу Радемахера) .
• Бона, Миклош (2002). Прогулка по комбинаторике: Введение в перечисление и теорию графов . World Scientific Publishing. ISBN 981-02-4900-4.(элементарное введение в тему целочисленных разбиений, включая обсуждение графов Феррерса)
• Харди, ГХ ; Райт, ЭМ (2008) [1938]. Введение в теорию чисел . Переработано Д. Р. Хит-Брауном и Дж. Х. Сильверманом . Предисловие Эндрю Уайлса . (6-е изд.). Оксфорд: Oxford University Press . ISBN 978-0-19-921986-5. MR  2445243. Zbl  1159.11001.
• Lehmer, DH (1939). «Об остатке и сходимости ряда для функции распределения». Trans. Amer. Math. Soc . 46 : 362–373. doi : 10.1090/S0002-9947-1939-0000410-9 . MR  0000410. Zbl  0022.20401.Предоставляет основную формулу (без производных), остаток и старую форму для A _k ( n ).)
• Gupta, Hansraj; Gwyther, CE; Miller, JCP (1962). Королевское математическое общество. Таблицы . Том 4, Таблицы разбиений. (Имеет текст, почти полную библиографию, но они (и Абрамовиц) пропустили формулу Сельберга для A _k ( n ), которая есть у Уайтмена.)
• Macdonald, Ian G. (1979). Симметричные функции и многочлены Холла . Oxford Mathematical Monographs. Oxford University Press . ISBN 0-19-853530-9. Збл  0487.20007.(См. раздел I.1)
• Натансон, МБ (2000). Элементарные методы в теории чисел . Тексты для аспирантов по математике. Том 195. Springer-Verlag . ISBN 0-387-98912-9. Збл  0953.11002.
• Радемахер, Ганс (1974). Сборник статей Ганса Радемахера . Том v II. MIT Press. С. 100–07, 108–22, 460–75.
• Sautoy, Marcus Du. (2003). Музыка простых чисел . Нью-Йорк: Perennial-HarperCollins. ISBN 9780066210704.
• Стэнли, Ричард П. (1999). Перечислительная комбинаторика. Том 1 и 2. Cambridge University Press. ISBN 0-521-56069-1.
• Уайтмен, АЛ (1956). «Сумма, связанная с рядом для функции распределения». Pacific Journal of Mathematics . 6 (1): 159–176. doi : 10.2140/pjm.1956.6.159 . Zbl  0071.04004. (Предоставляет формулу Сельберга. Более старая форма — это конечное разложение Фурье Сельберга.)

Внешние ссылки

• «Разделение», Энциклопедия математики , EMS Press , 2001 [1994]
• Калькулятор разделов и составов
• Вайсштейн, Эрик В. «Перегородка». Математический мир .
• Wilf, Herbert S. Lectures on Integer Partitions (PDF) , архивировано (PDF) из оригинала 2021-02-24 , извлечено 2021-02-28
• Подсчет с использованием разделов со справочными таблицами к Он-лайн энциклопедии целочисленных последовательностей
• Запись целочисленных разделов в базе данных FindStat
• Модуль Integer::Partition Perl из CPAN
• Быстрые алгоритмы для генерации целочисленных разделов
• Генерация всех разделов: сравнение двух кодировок
• Грайм, Джеймс (28 апреля 2016 г.). "Partitions - Numberphile" (видео) . Брэди Харан . Архивировано из оригинала 2021-12-11 . Получено 5 мая 2016 г. .