Эквант

Outdated measure of planetary orbits

Основные элементы астрономии Птолемея , показывающие планету на эпицикле (маленький пунктирный круг), деференте (большой пунктирный круг), эксцентрике (×) и экванте (•).

Эквант (или punctum aequans ) — математическая концепция, разработанная Клавдием Птолемеем во II веке нашей эры для объяснения наблюдаемого движения планет. Эквант используется для объяснения наблюдаемого изменения скорости на разных этапах планетарной орбиты. Эта планетарная концепция позволила Птолемею сохранить теорию равномерного кругового движения, заявив, что путь небесных тел является равномерным вокруг одной точки и круговым вокруг другой точки.

У Птолемея нет слова для экванта – он использовал такие выражения, как «эксцентр, производящий среднее движение» ^{[1] .}

Размещение

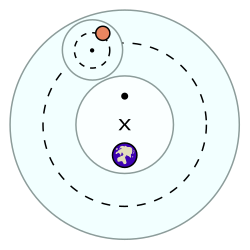
Точка экванта (показанная на схеме большим • ), расположена так, что она находится прямо напротив Земли из центра деферента , известного как эксцентрик (представленного × ). Планета или центр эпицикла ( меньшего круга, несущего планету) были задуманы движущимися с постоянной угловой скоростью относительно экванта. Для гипотетического наблюдателя, помещенного в точку экванта, центр эпицикла (обозначенный маленьким · ) будет казаться движущимся с постоянной угловой скоростью. Однако центр эпицикла не будет двигаться с постоянной скоростью вдоль своего деферента. ^[2]

Мотивация

Причиной внедрения экванта было сохранение видимости постоянного кругового движения небесных тел — давнего символа веры, созданного Аристотелем по философским причинам, а также обеспечение наилучшего соответствия вычислений наблюдаемых движений тел, особенно в отношении величины видимого ретроградного движения всех тел Солнечной системы, за исключением Солнца и Луны .

В модели экванта тело движется по круговой траектории, не центрированной на Земле. Скорость движущегося объекта будет меняться во время его движения по орбите вокруг внешнего круга (пунктирная линия), быстрее в нижней половине и медленнее в верхней половине, но движение считается равномерным, поскольку планета проходит равные углы за равное время с точки зрения точки экванта. Угловая скорость объекта неравномерна, если смотреть из любой другой точки внутри орбиты.

Применяемый без эпицикла (как для Солнца), использование экванта позволяет получить правильную угловую скорость в перигее и апогее с отношением (где — эксцентриситет орбиты ). Но по сравнению с кеплеровской орбитой метод экванта приводит к тому, что тело проводит слишком мало времени вдали от Земли и слишком много времени близко к Земле. Например, когда аномалия эксцентриса равна π/2, кеплеровская модель говорит, что с момента перигея пройдет время (где период равен , см. уравнение Кеплера ), тогда как модель экванта дает что немного больше. Более того, истинная аномалия в этой точке, согласно модели экванта, будет всего лишь тогда как в кеплеровской модели это что больше. Однако при малом эксцентриситете ошибка очень мала, будучи асимптотической к эксцентриситету в третьей степени. ${\displaystyle (1+e)^{2}/(1-e)^{2}}$ ${\displaystyle e}$ ${\displaystyle \pi /2-e}$ ${\displaystyle 2\pi }$ ${\displaystyle \pi /2-\arctan(e),}$ ${\displaystyle \pi /2+\arctan(e),}$ ${\displaystyle \pi /2+\arcsin(e),}$

Уравнение

Угол α, вершина которого находится в центре деферента, а стороны которого пересекают планету и эквант соответственно, является функцией времени t следующим образом:

${\displaystyle \alpha =\Omega t-\arcsin \left({\frac {E}{\ R\ }}\ \sin(\Omega t)\right)}$

где Ω — постоянная угловая скорость, наблюдаемая с экванта, который находится на расстоянии E, когда радиус деферента равен R. ^[3]

Открытие и использование

Птолемей ввел эквант в « Альмагесте ». ^[4] Доказательства того, что эквант был необходимой корректировкой физики Аристотеля, основывались на наблюдениях, сделанных им самим и неким «Теоном» (возможно, Теоном из Смирны ). ^[2]

Гиппарх

В моделях планетарного движения, которые предшествовали Птолемею , обычно приписываемым Гиппарху , эксцентрик и эпициклы уже были особенностью. Римский писатель Плиний в I веке н. э., который, по-видимому, имел доступ к трудам поздних греческих астрономов, и не будучи сам астрономом, все же правильно определил линии апсид для пяти известных планет и куда они указывали в зодиаке. ^[5] Такие данные требуют концепции эксцентрических центров движения.

До 430 года до нашей эры Метон и Эвктемон из Афин наблюдали различия в продолжительности сезонов . ^[2] Это можно наблюдать в продолжительности сезонов, определяемой равноденствиями и солнцестояниями, которые указывают, когда Солнце проходит 90 градусов по своему пути. Хотя другие пытались, Гиппарх вычислил и представил самые точные продолжительности сезонов около 130 года до нашей эры.

Согласно этим расчетам, весна длилась около ⁠94 +1/ 2 ⁠ дней , Лето около ⁠92+1/ 2 ⁠ , Падение около ⁠88+1/ 8 ⁠ , и зима около ⁠90+1/ 8 ⁠ , показывая, что времена года действительно имели различия в длине. Это позже использовалось в качестве доказательства зодиакального неравенства или видимости движения Солнца с непостоянной скоростью, при этом некоторые части его орбиты, включая его, двигались быстрее или медленнее. Годовое движение Солнца, как оно понималось греческой астрономией до этого момента, не учитывало этого, поскольку предполагалось, что Солнце имеет идеально круговую орбиту, которая была сосредоточена вокруг Земли, вокруг которой оно движется с постоянной скоростью. По словам астронома Гиппарха, перемещение центра пути Солнца немного в сторону от Земли удовлетворило бы наблюдаемое движение Солнца довольно безболезненно, таким образом делая орбиту Солнца эксцентричной. ^[2]

Большая часть того, что мы знаем о Гиппархе, дошла до нас через цитаты из его трудов Птолемеем. ^[4] Особенности моделей Гиппарха объясняли различия в продолжительности сезонов на Земле (известные как «первая аномалия») и появление ретроградного движения планет (известные как «вторая аномалия»). Но Гиппарх не смог сделать так, чтобы предсказания о местоположении и продолжительности ретроградного движения планет соответствовали наблюдениям; он мог сопоставить местоположение, или он мог сопоставить продолжительность, но не то и другое одновременно. ^[6]

Птолемей

Между моделью Гиппарха и Птолемея существовала промежуточная модель, которая была предложена для объяснения движения планет в целом на основе наблюдаемого движения Марса. В этой модели деферент имел центр, который также был эквантом, который можно было перемещать вдоль линии симметрии деферента, чтобы соответствовать ретроградному движению планеты. Однако эта модель все еще не соответствовала фактическому движению планет, как отметил Гиппарх. Это было верно, в частности, в отношении фактического расстояния и ширины ретроградных дуг, которые можно было увидеть позже согласно модели Птолемея и сравнить. ^[2]

Сам Птолемей исправил это противоречие, введя эквант в свое сочинение ^[4] , когда он отделил его от центра деферента, сделав и его, и центр деферента их собственными отдельными частями модели и сделав центр деферента неподвижным на протяжении всего движения планеты. ^[2] Местоположение определялось деферентом и эпициклом, в то время как продолжительность определялась равномерным движением вокруг экванта. Он сделал это без особых объяснений или обоснований того, как он пришел к точке его создания, решив только представить его формально и кратко с доказательствами, как в любой научной публикации. Даже в своих более поздних работах, где он признавал отсутствие объяснения, он не пытался объяснить дальше. ^[2]

Модель астрономии Птолемея использовалась как технический метод, который мог отвечать на вопросы, касающиеся астрологии и предсказания положений планет, в течение почти 1500 лет, хотя эквант и эксцентрик рассматривались многими поздними астрономами как нарушения чистой аристотелевской физики , которая предполагала, что все движение сосредоточено на Земле. Сообщалось, что модель космоса Птолемея была настолько популярной и революционной, что обычно очень трудно найти какие-либо подробности ранее используемых моделей, за исключением трудов самого Птолемея. ^[2]

От Коперника до Кеплера

На протяжении многих столетий исправление этих нарушений было заботой ученых, достигшей кульминации в решениях Ибн аль-Шатира и Коперника . Предсказания Птолемея, которые требовали постоянного пересмотра и исправления со стороны заинтересованных ученых на протяжении этих столетий, достигли кульминации в наблюдениях Тихо Браге в Ураниборге .

Только после того, как Иоганн Кеплер опубликовал свою работу «Новая астрономия» , основанную на данных, собранных им и Тихо в Ураниборге, модель небес Птолемея была полностью вытеснена новой геометрической моделью. ^{[7] [8]}

Критики

Эквант решил последнюю крупную проблему учета аномального движения планет, но некоторые считали, что он ставит под угрозу принципы древнегреческих философов, а именно равномерное круговое движение вокруг Земли. ^[9] Обычно предполагалось, что равномерность наблюдается из центра деферента, и поскольку это происходит только в одной точке, из любой другой точки наблюдается только неравномерное движение. Птолемей переместил точку наблюдения из центра деферента в точку экванта. Это можно рассматривать как нарушение аксиомы равномерного кругового движения.

Известные критики экванта включают персидского астронома Насира ад-Дина Туси , который разработал пару Туси в качестве альтернативного объяснения, ^[10] и Николая Коперника , чьей альтернативой была новая пара малых эпициклов для каждого деферента. Неприязнь к экванту была главной мотивацией для Коперника построить свою гелиоцентрическую систему. ^{[11] [12]}

Нарушение равномерного кругового движения вокруг центра деферента беспокоило многих мыслителей, особенно Коперника, который упоминает эквант как «чудовищную конструкцию» в «О вращении планет » . Смещение Коперником Земли из центра космоса устранило первостепенную необходимость в эпициклах Птолемея: оно объясняло ретроградное движение как эффект перспективы, обусловленный относительным движением Земли и планет. Однако оно не объясняло неравномерное движение Солнца и Луны, относительные движения которых Коперник не менял (хотя он и переделал вращение Солнца вокруг Земли в вращение Земли вокруг Солнца, эти два элемента геометрически эквивалентны). Перемещение центра планетарного движения с Земли на Солнце не устранило необходимость в чем-то, что могло бы объяснить неравномерное движение Солнца, для чего Коперник заменил эквант двумя (или несколькими) меньшими эпициклами вместо экванта.

Смотрите также

• Равноразмерный : Это синоним слова равновеликий, когда оно используется как прилагательное. ^{[ необходима цитата ]}

Ссылки

1. Клавдий Птолемей. Альмагест (PDF) .Перевод Г. Дж. Тумера.
2. Эванс, Джеймс (18 апреля 1984 г.). «О функции и вероятном происхождении экванта Птолемея» (PDF) . American Journal of Physics . 52 (12): 1080–89. Bibcode :1984AmJPh..52.1080E. doi :10.1119/1.13764 . Получено 29 августа 2014 г. .
3. См. уравнение 8 в "Эксцентрики, деференты, эпициклы и экванты". Mathpages .Кьютор выводит это сложным способом, используя производные и интегралы, но на самом деле это следует непосредственно из уравнения 3.
4. Птолемей, Клавдий . Μαθηματικὴ Σύνταξις (Mathēmatikē Syntaxis) [ Математический трактат («Альмагест») ]. IX, 5.
5. Гай Плиний Секунд . «Рассказ о мире и элементах: почему одни и те же звезды иногда кажутся более возвышенными, а иногда более близкими». Naturalis Historia [ Естественная история ]. Книга 2, Глава 13. Получено 7 августа 2014 г.
6. Equants, из части 1 Astronomia Nova Кеплера. Новая астрономия. science.larouchepac.com . Получено 1 августа 2014 г.— Отличное видео о влиянии экванта
7. Перриман, Майкл (2012-09-17). «История астрометрии». European Physical Journal H. 37 ( 5): 745–792. arXiv : 1209.3563 . Bibcode : 2012EPJH...37..745P. doi : 10.1140/epjh/e2012-30039-4. S2CID  119111979.
8. Бракко, К.; Провост, Ж.-П. (24 июля 2009 г.). «Если бы планета Марс не существовала: модель Кеплера equant и ее физические последствия». European Journal of Physics . 30 (5): 1085–1092. arXiv : 0906.0484 . Bibcode : 2009EJPh...30.1085B. doi : 10.1088/0143-0807/30/5/015. S2CID  46989038.
9. Ван Хелден. «Система Птолемея» . Проверено 20 марта 2014 г.
10. Крейг Г. Фрейзер (2006). Космос: историческая перспектива. Greenwood Publishing Group. стр. 39. ISBN 978-0-313-33218-0.
11. Кун, Томас (1957). Коперниканская революция . Издательство Гарвардского университета . С. 70–71. ISBN 978-0-674-17103-9.(авторское право возобновлено в 1985 году)
12. Кестлер, А. (1959). Лунатики: история изменения видения человеком вселенной . Хармондсворт, Великобритания: Penguin Books. стр. 322; см. также стр. 206 и ссылки там. «Лунатики» (архивная копия) – через Интернет-архив (archive.org).

Внешние ссылки

• Система Птолемея – в проекте «Галилео» Университета Райса
• Моделирование системы Птолемея на Java — в анимированном виртуальном планетарии Пола Стоддарда, Университет Северного Иллинойса.